2020-2021学年冀教版八年级数学下册20.3函数的表示课件(共25张ppt)
文档属性
| 名称 | 2020-2021学年冀教版八年级数学下册20.3函数的表示课件(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-13 00:00:00 | ||
图片预览








文档简介
冀教版八下
20.3 函数的表示
第二十章 函数
学习目标
冀教版八下
1.了解函数关系的三种表示方法;
2. 了解函数三种表示方法的特点,能选择适当的方法表示实际问题中的函数关系;
3.体会数学结合的思想方法.
一起探究
函数的表示方法
例1.过测量得出气温t(°C)与高度h(km)之间的一组数据如下表:
探究:
①t是h的函数吗?
是
②这是用什么形式来表示函数?
表格
我们把这种方法叫做:数值表
问题一:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}h/km
0
1
2
3
4
5
...
t/°C
24
18
12
6
0
-6
...
一起探究
通过测量得出气温t(°C)与高度h(km)之间的一组数据如下表:
观察表格发现,h每增加1km,t降低6°C.
②你能用一个数学式子表示这个规律吗?
t=24+6h
问题二:
①你能发现t随h变化的规律吗?
我们把这种方法叫做:表达式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}h/km
0
1
2
3
4
5
...
t/°C
24
18
12
6
0
-6
...
一起探究
以横轴表示高度,纵轴表示气温,建立平面直角坐标系,以h,t分别作点的横坐标和纵坐标,在直角坐标系中描点,连线,画出图形.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}h/km
0
1
2
3
4
5
...
t/°C
24
18
12
6
0
-6
...
18
6
24
12
30
-12
-6
O
1
2
3
4
5
-1
h
t
我们把这种方法叫做:图像法
新课学习
一、函数的图像
一般地,我们把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系中描点,所有这些点组成的图形就叫做这个函数的图像。
18
6
24
12
30
-12
-6
O
1
2
3
4
5
-1
h
t
1.概念
新课学习
一、函数的图像
2.画法
在自变量的取值范围内取值,函数才有意义,
因此要考虑自变量的取值范围.
从表达式中,可看出x可以取任意实数.
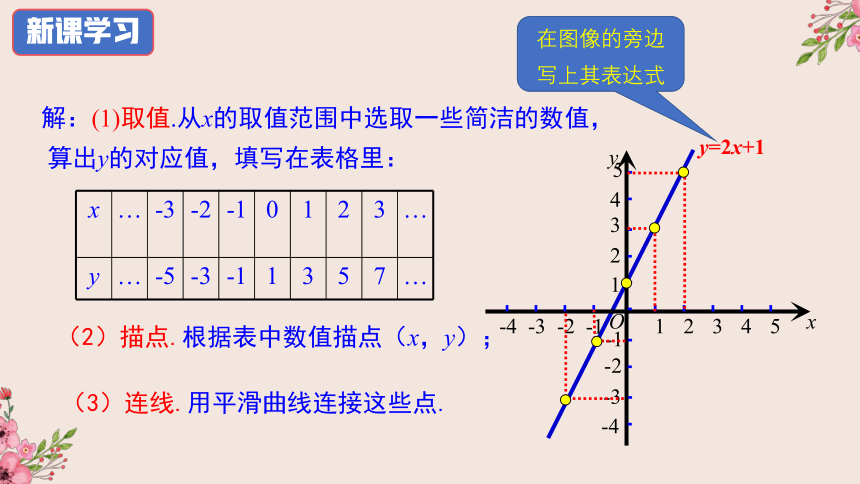
如:画函数y=2x+1的图像.
分析:
为表现出x为任意实数,可以正数、0、负数都取进去.
新课学习
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
(2)描点.根据表中数值描点(x,y);
(3)连线.用平滑曲线连接这些点.
x
…
-3
-2
-1
0
1
2
3
…
y
…
-5
-3
-1
1
3
5
7
…
解:(1)取值.从x的取值范围中选取一些简洁的数值,
算出y的对应值,填写在表格里:
在图像的旁边写上其表达式
新课学习
x/支
0
1
2
3
4
y/元
1
3
5
7
9
变式:一支铅笔2元,一块橡皮1元,买x支铅笔和1块橡皮所需的费用为y元,则y与x的函数表达式为y=2x+1,请你画出这个函数的图像.
分析:
在这个实际问题中,x为正整数.
此时,函数图像是一些不连续的点.
注意:自变量的取值范围对函数图像的影响.
归纳总结
1.列表——表中给出一些自变量的值及
其 ;
2.描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,描出表格中数值对应的各点;
3.连线——按照 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
自左向右
画函数图象的一般步骤:
新课学习
二、函数的三种表示方法的特点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}h/km
0
1
2
3
4
5
...
t/°C
24
18
12
6
0
-6
...
优点:
1.数值表
缺点:
只能反映函数中的部分数据.
具体反映了函数随自变量的数值对应关系.
新课学习
t=24+6h
2.函数表达式
优点:
能反映函数的整体特征,可以确定任意一对自变量与函数的对应值.
缺点:
反映函数图像的特征不形象.
新课学习
18
6
24
12
30
-12
-6
O
1
2
3
4
5
-1
h
t
3.图像
优点:
缺点:
不能得到具体值.
直观地反映了函数随自变量的变化而变化的规律.
新课学习
三、从函数图形中获取信息
例2.王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:
分析:
x轴:
小明爬山的时间
y轴:
两人离开山脚的距离
新课学习
解:由图象可知:小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米.
山顶离山脚的距离是300米,小强先爬上山.
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
O
新课学习
观察图像,小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷,此时两人距山脚240米.
(3)小强需多少时间追上爷爷?此时两人距山脚多少米?
O
新课学习
小强爬山300米用了10分钟,速度为300 ÷10=30米/分.
O
(4)谁的速度大?大多少?
x=8时,y=240,即爷爷用8分钟的时间爬山(240-60)米=180米,速度为180÷8=22.5米/分.
30-22.5=7.5
∴小强的速度大,大7.5米/分.
巩固练习
1.下图是护士统计一位新冠疑似病人的体温变化图,这位病人在16时的体温约是 ( ).
A.37.8 ℃ B.38 ℃ C.38.7 ℃ D.39.1 ℃
C
①能用数值表表示这个函数吗?
②能用表达式表示这个函数吗?
能
不能
巩固练习
2.李明手中有一组记录他从出生到24岁期间的身高情况表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄x/岁
0
3
6
9
12
15
18
21
24
身高h/cm
48
100
130
140
150
158
165
170
170.4
下列说法错误的是( ).
A.李明的身高增长速度总体上先快后慢;
B.李明的身高在21岁以后基本不长了;
C.李明的身高从0岁到24岁平均每年增高7.1cm;
D.李明的身高从0岁到24岁平均每年增高5.1cm.
C
①能用图像表示这个函数吗?
②能用表达式表示这个函数吗?
能
不能
巩固练习
3.学校组织学生到距离学校6千米的科技馆取参观,小明因事没能乘上学校的包车,于是准备在学校门口改乘出租车取科技馆,出租车收费标准如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}路程
收费
3千米以内(包含3千米)
8元
超过3千米,每增加1千米
1.8元
(1)写出出租车行驶路程x≥3时,与费用y之间的关系式;
(2)小明身上仅有14元,乘坐出租车够吗?
巩固练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}路程
收费
3千米以内(包含3千米)
8元
超过3千米,每增加1千米
1.8元
解:(1)y=8+1.8(x-3)=1.8x+2.6
(2)当x=6时
y=1.8×6+2.6=13.4(元)
13.4<14
∴够.
①能用图像表示这个函数吗?
②能用数值表表示这个函数吗?
能
能
巩固练习
4.一天,小明驾车从家去上班,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后小明加快速度继续匀速行驶赶到公司,工作结束后,小明驾车匀速返回.其中,x表示小明从家出发后所用时间,y表示小明离家的距离.下图中能反映y与x的函数关系的大致图像是 ( )
A
巩固练习
5.某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( ).
A.小强从家到公共汽车站步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
D
课堂小结
函数的表示
从图象获取信息
函数图象的画法
三种表示方法:图象法、列表法、表达式法
特定情况下可以互相转化
取值、描点、连线
同学们再见
20.3 函数的表示
第二十章 函数
学习目标
冀教版八下
1.了解函数关系的三种表示方法;
2. 了解函数三种表示方法的特点,能选择适当的方法表示实际问题中的函数关系;
3.体会数学结合的思想方法.
一起探究
函数的表示方法
例1.过测量得出气温t(°C)与高度h(km)之间的一组数据如下表:
探究:
①t是h的函数吗?
是
②这是用什么形式来表示函数?
表格
我们把这种方法叫做:数值表
问题一:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}h/km
0
1
2
3
4
5
...
t/°C
24
18
12
6
0
-6
...
一起探究
通过测量得出气温t(°C)与高度h(km)之间的一组数据如下表:
观察表格发现,h每增加1km,t降低6°C.
②你能用一个数学式子表示这个规律吗?
t=24+6h
问题二:
①你能发现t随h变化的规律吗?
我们把这种方法叫做:表达式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}h/km
0
1
2
3
4
5
...
t/°C
24
18
12
6
0
-6
...
一起探究
以横轴表示高度,纵轴表示气温,建立平面直角坐标系,以h,t分别作点的横坐标和纵坐标,在直角坐标系中描点,连线,画出图形.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}h/km
0
1
2
3
4
5
...
t/°C
24
18
12
6
0
-6
...
18
6
24
12
30
-12
-6
O
1
2
3
4
5
-1
h
t
我们把这种方法叫做:图像法
新课学习
一、函数的图像
一般地,我们把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系中描点,所有这些点组成的图形就叫做这个函数的图像。
18
6
24
12
30
-12
-6
O
1
2
3
4
5
-1
h
t
1.概念
新课学习
一、函数的图像
2.画法
在自变量的取值范围内取值,函数才有意义,
因此要考虑自变量的取值范围.
从表达式中,可看出x可以取任意实数.
如:画函数y=2x+1的图像.
分析:
为表现出x为任意实数,可以正数、0、负数都取进去.
新课学习
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
(2)描点.根据表中数值描点(x,y);
(3)连线.用平滑曲线连接这些点.
x
…
-3
-2
-1
0
1
2
3
…
y
…
-5
-3
-1
1
3
5
7
…
解:(1)取值.从x的取值范围中选取一些简洁的数值,
算出y的对应值,填写在表格里:
在图像的旁边写上其表达式
新课学习
x/支
0
1
2
3
4
y/元
1
3
5
7
9
变式:一支铅笔2元,一块橡皮1元,买x支铅笔和1块橡皮所需的费用为y元,则y与x的函数表达式为y=2x+1,请你画出这个函数的图像.
分析:
在这个实际问题中,x为正整数.
此时,函数图像是一些不连续的点.
注意:自变量的取值范围对函数图像的影响.
归纳总结
1.列表——表中给出一些自变量的值及
其 ;
2.描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,描出表格中数值对应的各点;
3.连线——按照 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
自左向右
画函数图象的一般步骤:
新课学习
二、函数的三种表示方法的特点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}h/km
0
1
2
3
4
5
...
t/°C
24
18
12
6
0
-6
...
优点:
1.数值表
缺点:
只能反映函数中的部分数据.
具体反映了函数随自变量的数值对应关系.
新课学习
t=24+6h
2.函数表达式
优点:
能反映函数的整体特征,可以确定任意一对自变量与函数的对应值.
缺点:
反映函数图像的特征不形象.
新课学习
18
6
24
12
30
-12
-6
O
1
2
3
4
5
-1
h
t
3.图像
优点:
缺点:
不能得到具体值.
直观地反映了函数随自变量的变化而变化的规律.
新课学习
三、从函数图形中获取信息
例2.王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:
分析:
x轴:
小明爬山的时间
y轴:
两人离开山脚的距离
新课学习
解:由图象可知:小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米.
山顶离山脚的距离是300米,小强先爬上山.
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
O
新课学习
观察图像,小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷,此时两人距山脚240米.
(3)小强需多少时间追上爷爷?此时两人距山脚多少米?
O
新课学习
小强爬山300米用了10分钟,速度为300 ÷10=30米/分.
O
(4)谁的速度大?大多少?
x=8时,y=240,即爷爷用8分钟的时间爬山(240-60)米=180米,速度为180÷8=22.5米/分.
30-22.5=7.5
∴小强的速度大,大7.5米/分.
巩固练习
1.下图是护士统计一位新冠疑似病人的体温变化图,这位病人在16时的体温约是 ( ).
A.37.8 ℃ B.38 ℃ C.38.7 ℃ D.39.1 ℃
C
①能用数值表表示这个函数吗?
②能用表达式表示这个函数吗?
能
不能
巩固练习
2.李明手中有一组记录他从出生到24岁期间的身高情况表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄x/岁
0
3
6
9
12
15
18
21
24
身高h/cm
48
100
130
140
150
158
165
170
170.4
下列说法错误的是( ).
A.李明的身高增长速度总体上先快后慢;
B.李明的身高在21岁以后基本不长了;
C.李明的身高从0岁到24岁平均每年增高7.1cm;
D.李明的身高从0岁到24岁平均每年增高5.1cm.
C
①能用图像表示这个函数吗?
②能用表达式表示这个函数吗?
能
不能
巩固练习
3.学校组织学生到距离学校6千米的科技馆取参观,小明因事没能乘上学校的包车,于是准备在学校门口改乘出租车取科技馆,出租车收费标准如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}路程
收费
3千米以内(包含3千米)
8元
超过3千米,每增加1千米
1.8元
(1)写出出租车行驶路程x≥3时,与费用y之间的关系式;
(2)小明身上仅有14元,乘坐出租车够吗?
巩固练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}路程
收费
3千米以内(包含3千米)
8元
超过3千米,每增加1千米
1.8元
解:(1)y=8+1.8(x-3)=1.8x+2.6
(2)当x=6时
y=1.8×6+2.6=13.4(元)
13.4<14
∴够.
①能用图像表示这个函数吗?
②能用数值表表示这个函数吗?
能
能
巩固练习
4.一天,小明驾车从家去上班,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后小明加快速度继续匀速行驶赶到公司,工作结束后,小明驾车匀速返回.其中,x表示小明从家出发后所用时间,y表示小明离家的距离.下图中能反映y与x的函数关系的大致图像是 ( )
A
巩固练习
5.某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( ).
A.小强从家到公共汽车站步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
D
课堂小结
函数的表示
从图象获取信息
函数图象的画法
三种表示方法:图象法、列表法、表达式法
特定情况下可以互相转化
取值、描点、连线
同学们再见
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
