2020-2021学年沪科版数学七年级下册10.1相交线-课件(共34张ppt)
文档属性
| 名称 | 2020-2021学年沪科版数学七年级下册10.1相交线-课件(共34张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-13 09:17:57 | ||
图片预览




文档简介
(共34张PPT)
10.1
相交线
第10章
相交线、平行线与平移
节日的夜晚,广场上两个激光发射器发射出在同一平面上的两条直线。如果将这两束光线看成两条直线,那么当发射器左右摆动时,这两条直线有什么样的位置关系?有哪些特殊的位置关系?
观察与思考
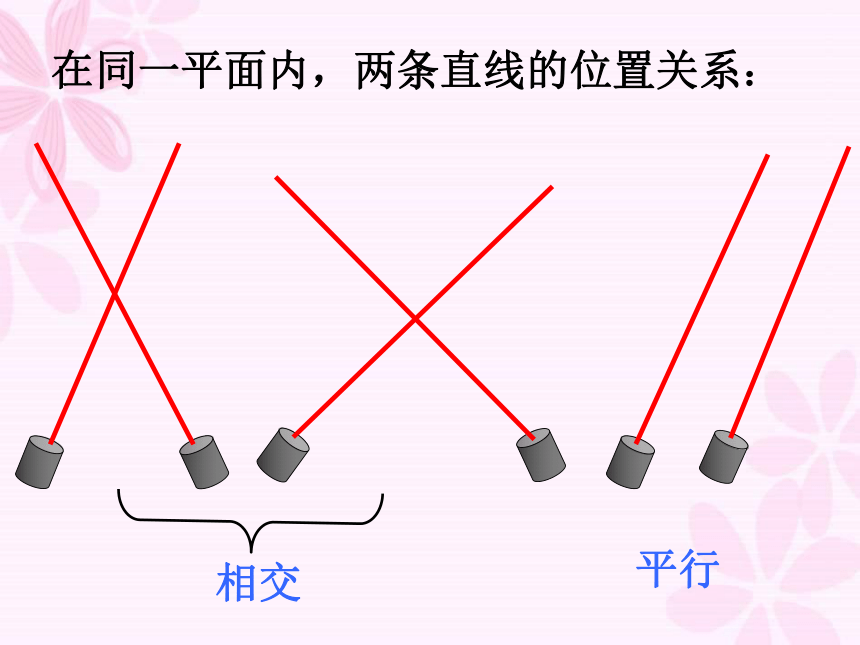
在同一平面内,两条直线的位置关系:
平行
相交
画板O
A
B
C
D
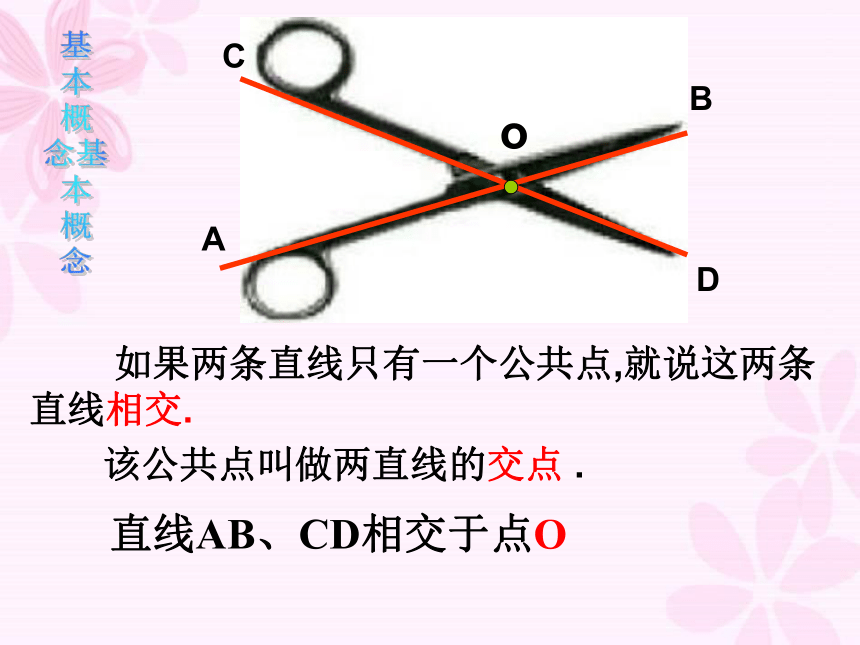
直线AB、CD相交于点O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点
.
o
基
本
概
念
探
究
思
考
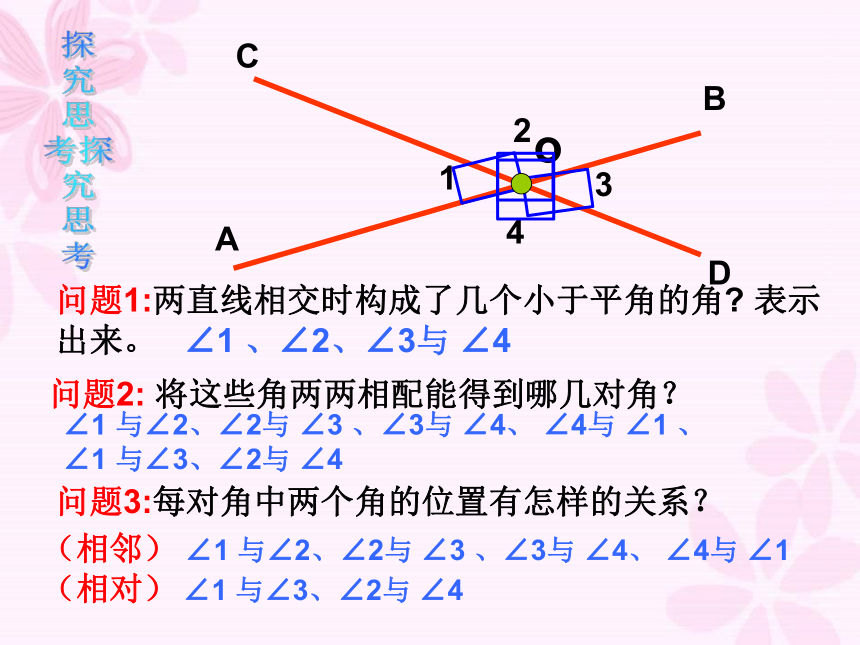
问题1:两直线相交时构成了几个小于平角的角?
表示出来。
∠1
、∠2、∠3与
∠4
问题2:
将这些角两两相配能得到哪几对角?
∠1
与∠2、∠2与
∠3
、∠3与
∠4、
∠4与
∠1
、
∠1
与∠3、∠2与
∠4
问题3:每对角中两个角的位置有怎样的关系?
(相邻)
∠1
与∠2、∠2与
∠3
、∠3与
∠4、
∠4与
∠1
(相对)
∠1
与∠3、∠2与
∠4
2
A
B
C
D
1
4
3
o
A
B
C
D
1
4
3
o
2
问题
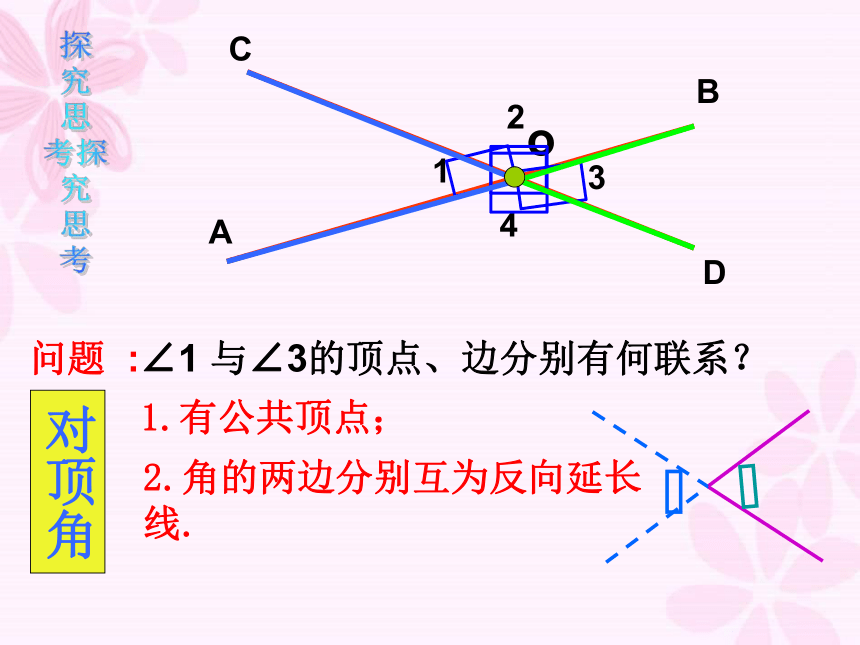
:∠1
与∠3的顶点、边分别有何联系?
探
究
思
考
1.有公共顶点;
2.角的两边分别互为反向延长线.
对顶角
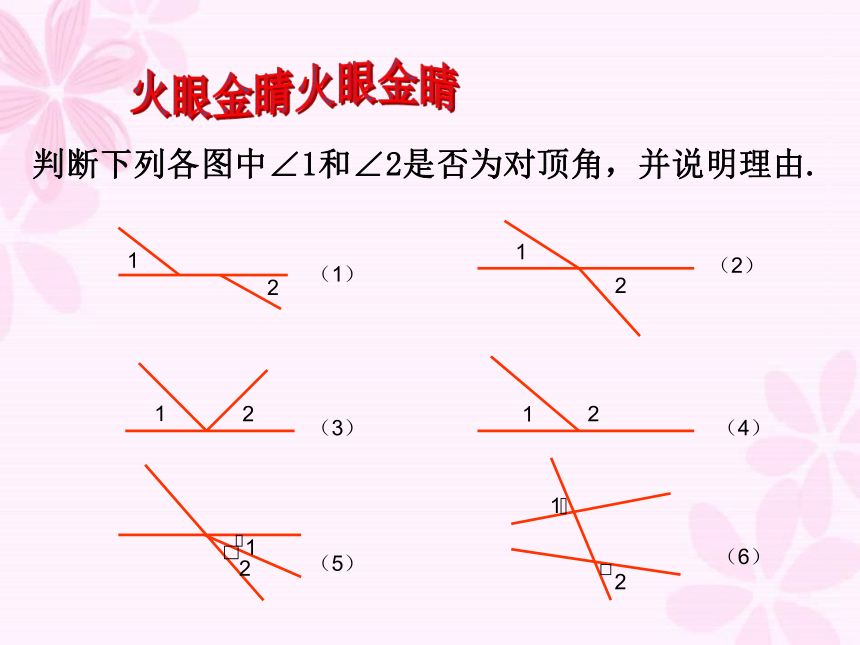
判断下列各图中∠1和∠2是否为对顶角,并说明理由.
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
(5)
(6)
1
2
1
2
火眼金睛
A
B
C
D
1
4
3
o
2
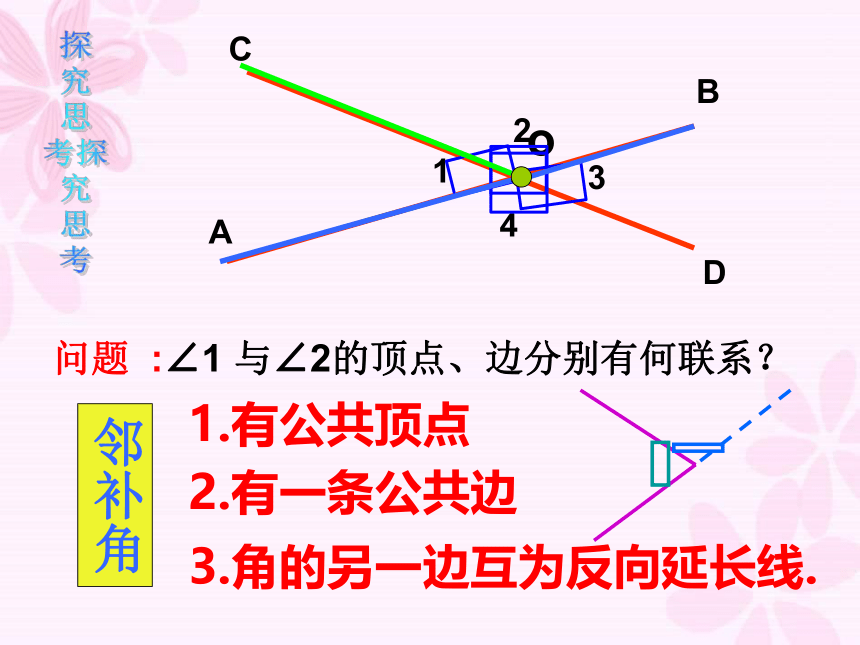
问题
:∠1
与∠2的顶点、边分别有何联系?
探
究
思
考
邻补角
2.有一条公共边
3.角的另一边互为反向延长线.
1.有公共顶点
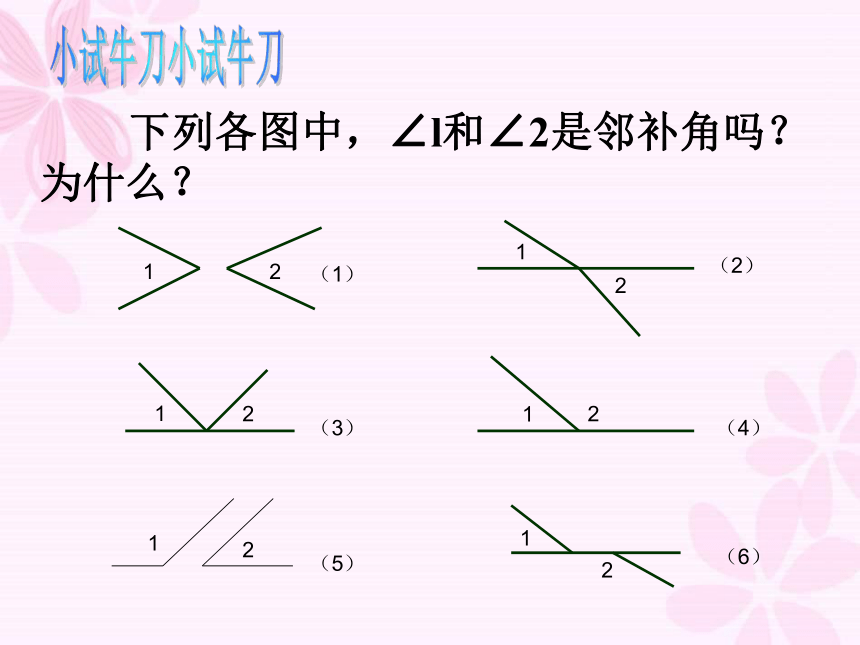
下列各图中,∠l和∠2是邻补角吗?为什么?
小试牛刀
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
(5)
(6)
1
2
1
2
2
1
2
1
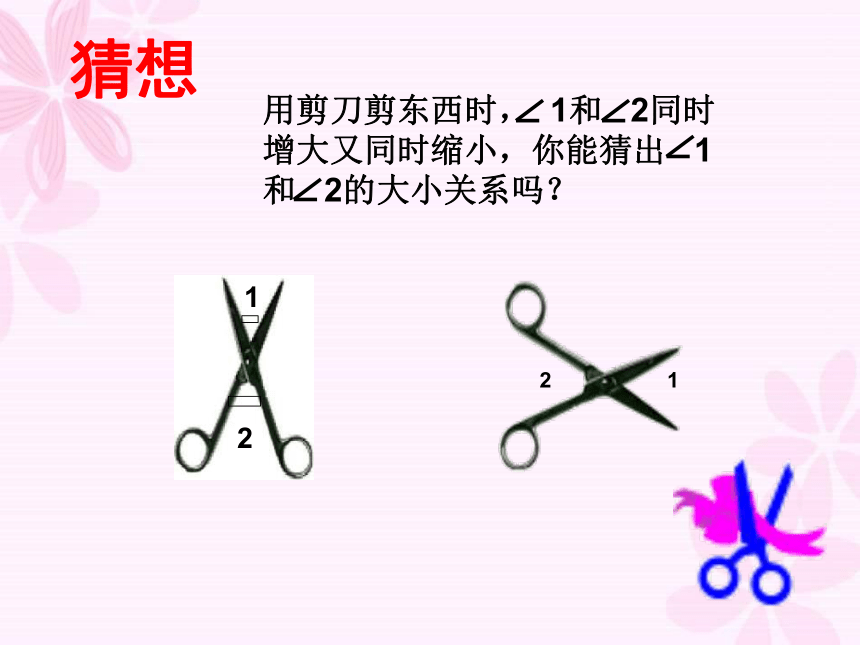
用剪刀剪东西时,
1和
2同时
增大又同时缩小,你能猜出
1
和
2的大小关系吗?
猜想
剪刀剪东西的过程中,∠1和∠3的大小上有什么关系?
动手量一量,你会有所发现!
所以∠1=∠3
同理∠2=∠4
∠2与∠3互补
因为∠1与∠2互补
(邻补角定义)
(同角的补角相等)
对顶角相等
探
究
思
考
A
B
C
D
1
4
3
o
2
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4
1、有公共顶点
特征
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
两直线相交
2、角的两边分别互为反向延长线
名称
性质
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
归纳总结
1
2
3
4
例1
:
如图,已知直线a、b相交.
⑴若∠1=40°,求∠2、
∠3、
∠4的度数.
⑵若∠1+
∠3=180
°,求各角的度数.
a
b
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
如果∠1与∠2是对顶角,且∠1=26°则∠2=
_
26°
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
两条直线相交得到四个角,其中一个角是30°,则其余的三个角的度数分别是______________________.
150
°,
30
°
,150
°
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
判断题
(1)相等的角是对顶角。
(
)
(2)有公共顶点且相等的两个角是对顶角。
(
)
(3)若这两个角不是对顶角,则这两个角不相等。
(
)
(4)两条直线相交所构成的四个角中有一个角是直角,那么其余的三个角也是直角。
(
)
×
√
×
×
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
l1
l2
l3
o
1
3
2
6
5
4
如图,三条直线
交于点O,求
1+
3+
5等于多少度?
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
B
A
C
三条直线两两相交,一共形成多少对对顶角?
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
恭喜中大奖
游戏
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
如图,已知直线AB、CD相交于点O,OA平分∠EOC,
∠
EOC=70°,求∠
BOD的度数。
E
A
C
D
B
O
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
直线AB、CD交于点O,OE分∠BOD为两部分,且∠BOE
﹕
∠
DOE
=2
﹕
5,已知∠AOC=70°。求∠DOE的度数。
A
O
E
B
C
D
两条直线相交
对顶角:相等
邻补角:互补
特殊情况
相交成直角
课堂小结
一般情况
?
思考:
两条直线相交于一点,有几对对顶角?
三条直线相交于一点,有几对对顶角?
四条直线相交于一点,有几对对顶角?
n
条直线相交于一点,有几对对顶角?
拓展提高
10.1
相交线
第10章
相交线、平行线与平移
节日的夜晚,广场上两个激光发射器发射出在同一平面上的两条直线。如果将这两束光线看成两条直线,那么当发射器左右摆动时,这两条直线有什么样的位置关系?有哪些特殊的位置关系?
观察与思考
在同一平面内,两条直线的位置关系:
平行
相交
画板O
A
B
C
D
直线AB、CD相交于点O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点
.
o
基
本
概
念
探
究
思
考
问题1:两直线相交时构成了几个小于平角的角?
表示出来。
∠1
、∠2、∠3与
∠4
问题2:
将这些角两两相配能得到哪几对角?
∠1
与∠2、∠2与
∠3
、∠3与
∠4、
∠4与
∠1
、
∠1
与∠3、∠2与
∠4
问题3:每对角中两个角的位置有怎样的关系?
(相邻)
∠1
与∠2、∠2与
∠3
、∠3与
∠4、
∠4与
∠1
(相对)
∠1
与∠3、∠2与
∠4
2
A
B
C
D
1
4
3
o
A
B
C
D
1
4
3
o
2
问题
:∠1
与∠3的顶点、边分别有何联系?
探
究
思
考
1.有公共顶点;
2.角的两边分别互为反向延长线.
对顶角
判断下列各图中∠1和∠2是否为对顶角,并说明理由.
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
(5)
(6)
1
2
1
2
火眼金睛
A
B
C
D
1
4
3
o
2
问题
:∠1
与∠2的顶点、边分别有何联系?
探
究
思
考
邻补角
2.有一条公共边
3.角的另一边互为反向延长线.
1.有公共顶点
下列各图中,∠l和∠2是邻补角吗?为什么?
小试牛刀
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
(5)
(6)
1
2
1
2
2
1
2
1
用剪刀剪东西时,
1和
2同时
增大又同时缩小,你能猜出
1
和
2的大小关系吗?
猜想
剪刀剪东西的过程中,∠1和∠3的大小上有什么关系?
动手量一量,你会有所发现!
所以∠1=∠3
同理∠2=∠4
∠2与∠3互补
因为∠1与∠2互补
(邻补角定义)
(同角的补角相等)
对顶角相等
探
究
思
考
A
B
C
D
1
4
3
o
2
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4
1、有公共顶点
特征
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
两直线相交
2、角的两边分别互为反向延长线
名称
性质
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
归纳总结
1
2
3
4
例1
:
如图,已知直线a、b相交.
⑴若∠1=40°,求∠2、
∠3、
∠4的度数.
⑵若∠1+
∠3=180
°,求各角的度数.
a
b
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
如果∠1与∠2是对顶角,且∠1=26°则∠2=
_
26°
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
两条直线相交得到四个角,其中一个角是30°,则其余的三个角的度数分别是______________________.
150
°,
30
°
,150
°
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
判断题
(1)相等的角是对顶角。
(
)
(2)有公共顶点且相等的两个角是对顶角。
(
)
(3)若这两个角不是对顶角,则这两个角不相等。
(
)
(4)两条直线相交所构成的四个角中有一个角是直角,那么其余的三个角也是直角。
(
)
×
√
×
×
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
l1
l2
l3
o
1
3
2
6
5
4
如图,三条直线
交于点O,求
1+
3+
5等于多少度?
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
B
A
C
三条直线两两相交,一共形成多少对对顶角?
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
恭喜中大奖
游戏
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
如图,已知直线AB、CD相交于点O,OA平分∠EOC,
∠
EOC=70°,求∠
BOD的度数。
E
A
C
D
B
O
1
8
7
6
5
4
3
2
一起砸金蛋
游戏
请你来解题
游戏
直线AB、CD交于点O,OE分∠BOD为两部分,且∠BOE
﹕
∠
DOE
=2
﹕
5,已知∠AOC=70°。求∠DOE的度数。
A
O
E
B
C
D
两条直线相交
对顶角:相等
邻补角:互补
特殊情况
相交成直角
课堂小结
一般情况
?
思考:
两条直线相交于一点,有几对对顶角?
三条直线相交于一点,有几对对顶角?
四条直线相交于一点,有几对对顶角?
n
条直线相交于一点,有几对对顶角?
拓展提高
