江苏省苏州市吴江区2020-2021学年高二下学期期中考试数学试题 Word版含解析
文档属性
| 名称 | 江苏省苏州市吴江区2020-2021学年高二下学期期中考试数学试题 Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 78.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 11:23:04 | ||
图片预览




文档简介
江苏省苏州市吴江区2020-2021学年高二下学期数学期中考试试卷(解析版)
一、单选题(共9题;共45分)
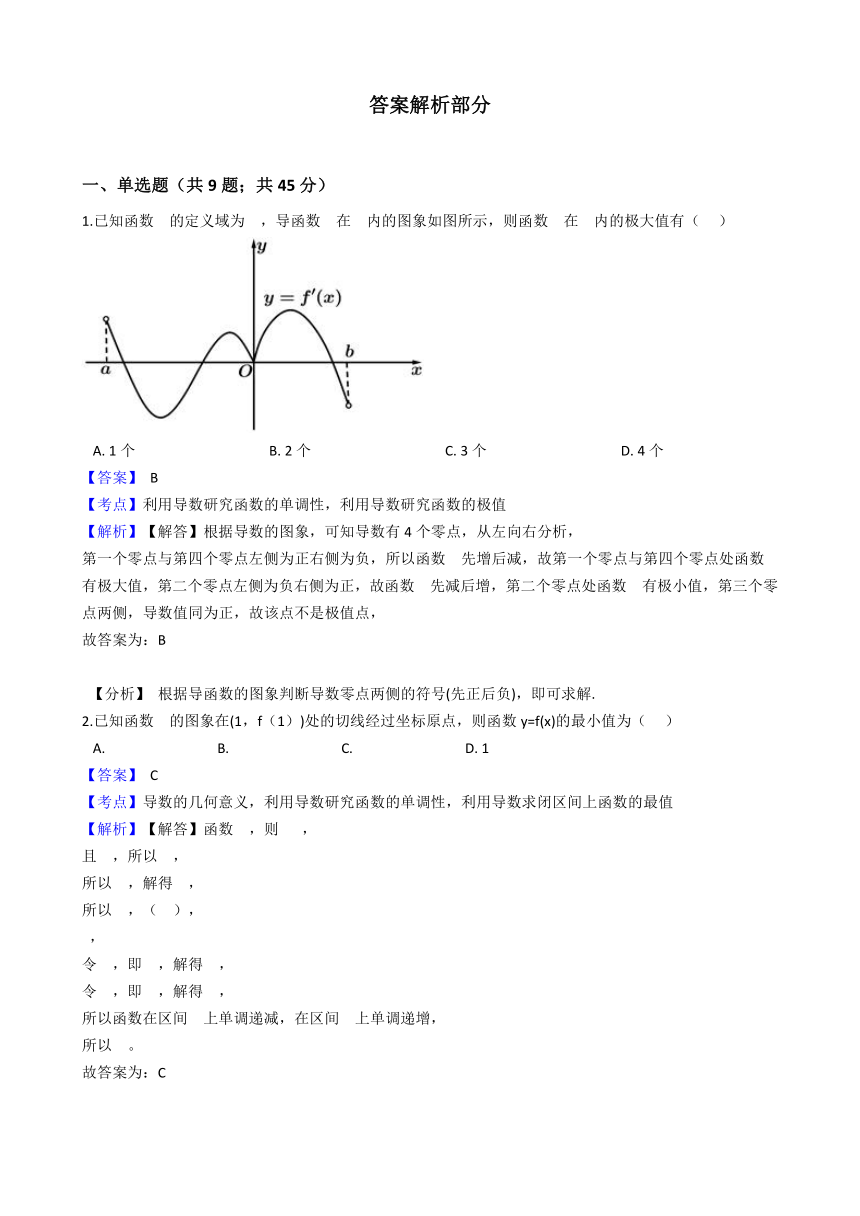
1.已知函数 的定义域为 ,导函数 在 内的图象如图所示,则函数 在 内的极大值有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.已知函数 的图象在(1,f(1))处的切线经过坐标原点,则函数y=f(x)的最小值为(??? )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?1
3.若函数 的极大值点与极大值分别为a , b , 则(??? )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
4.设函数 ,则 是(??? )
A.?奇函数,且在 上是增函数??????????????????????????B.?奇函数,且在 上是减函数
C.?偶函数,且在 上是增函数??????????????????????????D.?偶函数,且在 上是减函数
5.已知函数 的定义域为 ,其导函数是 .有 ,则关于x的不等式 的解集为(??? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
6.某校开展学农活动时进行劳动技能比赛,通过初选,选甲?乙?丙?丁?戊共5名同学进行决赛,决出第1名到第5名的名次.甲?乙?丙三人去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”;对丙说“甲比你好”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有(??? )
A.?24种????????????????????????????????????B.?16种????????????????????????????????????C.?18种????????????????????????????????????D.?20种
7.已知 ,则 (??? )
A.?-10????????????????????????????????????????B.?10????????????????????????????????????????C.?-45????????????????????????????????????????D.?45
8.埃及金字塔之谜是人类史上最大的谜,它的神奇远远超过了人类的想象.在埃及金字塔内有一组神秘的数字142857,因为 ,…,所以这组数字又叫“走马灯数”.该组数字还有如下发现: ,…,若从这组神秘数字中任选3个数字构成一个三位数x , 剩下的三个数字构成另一个三位数y , ,将所有可能的三位数x按从小到大依次排序,则第12个三位数x为(??? )
A.?214??????????????????????????????????????B.?215??????????????????????????????????????C.?248??????????????????????????????????????D.?284
9.我国古代著名的数学著作中,《周碑算经》?《九章算术》?《孙子算经》?《五曹算经》?《夏侯阳算经》?《孙丘建算经》?《海岛算经》?《五经算术》?《级术》和《纠古算经》,称为“算经十书”,某老师将其中的《周碑算经》?《九章算术》?《孙子算经》?《五经算术》?《级术》和《纠古算经》6本书分给4名数学爱好者,其中每人至少一本,则不同的分配方法的种数为(??? )
A.???????????B.???????????C.???????????D.?
二、多选题(共3题;共15分)
10.函数 的定义域为R , 它的导函数 的部分图象如图所示,则下面结论正确的是(??? )
A.?在 上函数 为增函数???????????????????????????B.?在 上函数 为增函数
C.?在 上函数 有极大值????????????????????????????D.? 是函数 在区间 上的极小值点
11.定义在R上的函数 ,其导函数 满足 ,则下列不等关系正确的是(??? )
A.??????????????B.??????????????C.??????????????D.?
12.已知 的二项展开式中系数之和为729,则下列结论正确的是(??? )
A.?二项展开式中各项二项式系数之和为 ??????????????B.?二项展开式中二项式系数最大的项为
C.?二项展开式中无常数项???????????????????????????????????????D.?二项展开式中系数最大的项为
三、填空题(共4题;共20分)
13.已知函数 与 的图像上存在关于原点对称的对称点,则实数a的取值范围是________.
14.在 的展开式中,若 ,则 ________.
15.酒杯的形状为倒立的圆锥(如图),杯深9cm,上口宽6 cm,水以 的流量倒入杯中,当水深为3cm时,水升高的瞬时变化率为________.
16.若函数 的导函数 存在导数,记 的导数为 .如果对 x (a,b),都有 ,则 有如下性质: ,其中n , , ,…, (a,b).若 ,则 =________;在锐角△ABC中,根据上述性质推断:sinA+sinB+sinC的最大值为________.
四、解答题(共6题;共70分)
17.在下面两个条件中任选一个条件,补充在后面问题中的横线上,并完成解答.条件①:“展开式中所有项的系数之和与二项式系数之和的比为64”;条件②:“展开式中前三项的二项式系数之和为22”.
问题:已知二项式 ,若___________(填写条件前的序号),
(1)求展开式中系数最大的项;
(2)求 中含 项的系数.
18.用0,1,2,3,4,5这六个数字:(最后运算结果请以数字作答)
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的四位数?
(3)能组成多少个无重复数字且比1230大的四位数?
19.已知 展开式的二项式系数和为512,且
(1)求 的值;
(2)求 被6整除的余数.
20.已知 .
(1)当 时,求 在 上的最大值;
(2)当 时,讨论 的单调性.
21.已知函数 .
(1)求 过 的切线方程;
(2)若 在 上的最大值为 ,求证: .
22.已知函数 (其中e为自然对数的底数).
(1)求函数 的极值;
(2)当 时,若 恒成立,求实数b的取值范围.
答案解析部分
一、单选题(共9题;共45分)
1.已知函数 的定义域为 ,导函数 在 内的图象如图所示,则函数 在 内的极大值有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
【答案】 B
【考点】利用导数研究函数的单调性,利用导数研究函数的极值
【解析】【解答】根据导数的图象,可知导数有4个零点,从左向右分析,
第一个零点与第四个零点左侧为正右侧为负,所以函数 先增后减,故第一个零点与第四个零点处函数 有极大值,第二个零点左侧为负右侧为正,故函数 先减后增,第二个零点处函数 有极小值,第三个零点两侧,导数值同为正,故该点不是极值点,
故答案为:B
【分析】 根据导函数的图象判断导数零点两侧的符号(先正后负),即可求解.
2.已知函数 的图象在(1,f(1))处的切线经过坐标原点,则函数y=f(x)的最小值为(??? )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?1
【答案】 C
【考点】导数的几何意义,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
【解析】【解答】函数 ,则 ,
且 ,所以 ,
所以 ,解得 ,
所以 ,( ),
,
令 ,即 ,解得 ,
令 ,即 ,解得 ,
所以函数在区间 上单调递减,在区间 上单调递增,
所以 。
故答案为:C
【分析】利用求导的方法切成函数在切点处的切线的斜率,再利用切点的横坐标求出切点的纵坐标,进而求出切点的坐标,再利用点斜式求出函数在切点处的切线方程,再利用切线经过坐标原点,结合代入法,进而求出a的值,从而求出函数的解析式,再利用求导的方法判断函数的单调性,再利用函数的单调性求出函数的最小值。
3.若函数 的极大值点与极大值分别为a , b , 则(??? )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
【答案】 C
【考点】利用导数研究函数的单调性,利用导数研究函数的极值
【解析】【解答】∵ ,
∴ 或 ,
, 或 ,
∴ 在 单调递增,在 单调递减,
∴ 为极大值点,且 ,
∴ , ,
∴ ,
故答案为:C.
【分析】 先对函数求导,然后结合导数分析函数的单调性,进而可求函数的极大值与极大值点,从而可求.
4.设函数 ,则 是(??? )
A.?奇函数,且在 上是增函数??????????????????????????B.?奇函数,且在 上是减函数
C.?偶函数,且在 上是增函数??????????????????????????D.?偶函数,且在 上是减函数
【答案】 A
【考点】复合函数的单调性,函数奇偶性的判断,奇偶性与单调性的综合
【解析】【解答】 ? 的定义域为
而 ,所以 为奇函数;
在 上, ,
因为 在 上为增函数 在 上为减函数,
所以 在 上是增函数
故答案为:A.
【分析】 根据题意先检验f(-x)与f(x)的关系,然后结合复合函数单调性及奇偶性的定义进行检验即可判断.
5.已知函数 的定义域为 ,其导函数是 .有 ,则关于x的不等式 的解集为(??? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
【答案】 B
【考点】函数单调性的性质,利用导数研究函数的单调性
【解析】【解答】由题意,函数 满足 ,
令 ,则
函数 是定义域 内的单调递减函数,
由于 ,关于 的不等式 可化为 ,
即 ,所以 且 ,解得 ,
不等式 的解集为 .
故答案为:B
【分析】 根据题意令 , 求导,结合题意可得g(x)在上单调递减;而得到从而可得答案.
6.某校开展学农活动时进行劳动技能比赛,通过初选,选甲?乙?丙?丁?戊共5名同学进行决赛,决出第1名到第5名的名次.甲?乙?丙三人去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”;对丙说“甲比你好”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有(??? )
A.?24种????????????????????????????????????B.?16种????????????????????????????????????C.?18种????????????????????????????????????D.?20种
【答案】 C
【考点】排列、组合及简单计数问题
【解析】【解答】由题意可得,第1名不可能是甲?乙?丙,只能是丁或戊;第5名不可能是甲乙,只能是丙或丁或戊;因此可分如下三种情况:
若甲是第2名,先考虑乙,则有 种情况,再考虑丙,则有 种情况,最后排丁?戊,则有 种情况,即此时所包含的情况有: 种;
若甲是第3名,当乙是第4名时,丙只能是第5名,只需考虑丁?戊的排列,此时有 种情况;当乙是第2名时,丙可以有 种选择,最后排丁?戊,则有 种情况;此时包含的情况共有 种;
若甲是第4名,则丙是第5名,而乙有 种选择,最后排丁?戊,则有 种情况,;此时所包含的情况有 ;
综上,从这个回答中分析这5人的名次排列顺序可能出现的种类有 种.
故答案为:C.
【分析】 根据题意可得甲乙不是最后一名或第一名,根据排列组合以及分类计数原理计算出结果即可。
7.已知 ,则 (??? )
A.?-10????????????????????????????????????????B.?10????????????????????????????????????????C.?-45????????????????????????????????????????D.?45
【答案】 D
【考点】二项式系数的性质
【解析】【解答】
, .
故答案为:D
【分析】利用二项式的通项公式,结合已知条件代入数值计算出结果即可。
8.埃及金字塔之谜是人类史上最大的谜,它的神奇远远超过了人类的想象.在埃及金字塔内有一组神秘的数字142857,因为 ,…,所以这组数字又叫“走马灯数”.该组数字还有如下发现: ,…,若从这组神秘数字中任选3个数字构成一个三位数x , 剩下的三个数字构成另一个三位数y , ,将所有可能的三位数x按从小到大依次排序,则第12个三位数x为(??? )
A.?214??????????????????????????????????????B.?215??????????????????????????????????????C.?248??????????????????????????????????????D.?284
【答案】 C
【考点】排列、组合及简单计数问题
【解析】【解答】∵1,4,7,2,8,5,这六个数中,1+8=9,2+7=9,4+5=9,共3组
要使六个数字中任意取出3个数字构成一个三位数 ,剩下的三个数字构成另一个三位数 ,且 ,所以 从小到大排列为: ,故第12个三位数x为248.
故答案为:C
【分析】 根据题意,在数字142857中,两个数字之和为9的组合有3个,据此依次分析数字x、y的百位、十位、个位数字的情况,即可求出.
9.我国古代著名的数学著作中,《周碑算经》?《九章算术》?《孙子算经》?《五曹算经》?《夏侯阳算经》?《孙丘建算经》?《海岛算经》?《五经算术》?《级术》和《纠古算经》,称为“算经十书”,某老师将其中的《周碑算经》?《九章算术》?《孙子算经》?《五经算术》?《级术》和《纠古算经》6本书分给4名数学爱好者,其中每人至少一本,则不同的分配方法的种数为(??? )
A.???????????B.???????????C.???????????D.?
【答案】 B
【考点】列举法计算基本事件数及事件发生的概率,排列、组合及简单计数问题
【解析】【解答】根据题意,第一类,从6本书中取出3本视作一本书,连同剩余的3本分配给4个人,共有 种分法,
第二类,从6本书中取出2本书,再从剩余4本书中取出2本书,平均分堆后连同剩余2本,视作4本书分配给4个人,共有 ,
由分类加法计数原理可得,不同的分配方法的种数为 ,
故答案为:B
【分析】根据题意6本分给4名数学爱好者,每人至少一本,则把6本书为6本书为(3,1,11)和(2,2,1,1),再分配给4名数学爱好者, 再由概率的定义代入数值计算出结果即可。
二、多选题(共3题;共15分)
10.函数 的定义域为R , 它的导函数 的部分图象如图所示,则下面结论正确的是(??? )
A.?在 上函数 为增函数???????????????????????????B.?在 上函数 为增函数
C.?在 上函数 有极大值????????????????????????????D.? 是函数 在区间 上的极小值点
【答案】 A,C
【考点】函数的图象,利用导数研究函数的单调性,函数在某点取得极值的条件
【解析】【解答】由图象可知 在区间 和 上 , 递增;在区间 上 , 递减.
所以A选项正确,B选项错误.
在区间 上, 有极大值为 ,C选项正确.
在区间 上, 是 的极小值点,D选项错误.
故答案为:AC
【分析】由已知条件,结合图象即可得出导函数的性质,由此得出函数的单调性,利用函数的单调性即可求出函数的极值,对选项逐一判断即可得出答案。
11.定义在R上的函数 ,其导函数 满足 ,则下列不等关系正确的是(??? )
A.??????????????B.??????????????C.??????????????D.?
【答案】 A,B,D
【考点】函数单调性的性质,利用导数研究函数的单调性
【解析】【解答】令 ,则 ,
, 在 上恒成立,
在 上单调递增,
对A, ,A符合题意;
对B, ,B符合题意;
对C, ,C不符合题意;
对D, ,D符合题意;
故答案为:ABD.
【分析】根据题意构造函数 , 并对其求导结合导函数的性质即可得出函数的单调性,由函数的单调性对选项逐一判断即可得出答案。
12.已知 的二项展开式中系数之和为729,则下列结论正确的是(??? )
A.?二项展开式中各项二项式系数之和为 ??????????????B.?二项展开式中二项式系数最大的项为
C.?二项展开式中无常数项???????????????????????????????????????D.?二项展开式中系数最大的项为
【答案】 A,B
【考点】二项式定理,二项式系数的性质
【解析】【解答】令 ,则 二项展开式系数和为 ,解得: ;
展开式的通项公式为 ;
对于A,由 知其二项式系数和为 ,A符合题意;
对于B,当 时,二项式系数最大,则所求项为 ,B符合题意;
对于C,令 ,解得: ,则展开式第5项为常数项,C不符合题意;
对于D,分别令 ,可得展开式为 ,由此可确定系数最大的项为 ,D不符合题意.
故答案为:AB.
【分析】 由题意利用二项展开式的通项公式,再结合二项式系数的性质,对选项逐一判断即可得出答案。
三、填空题(共4题;共20分)
13.已知函数 与 的图像上存在关于原点对称的对称点,则实数a的取值范围是________.
【答案】
【考点】函数的值域,奇偶函数图象的对称性,利用导数研究函数的单调性
【解析】【解答】函数 与 的图像上存在关于原点对称的对称点,
∴方程 ,即 在 上有解,
∴方程 在 有解.
设 , ,且 为 的切线,
设切点为 ,
由 得 ,
则有 ,解得 .
由图象可得,要使直线 和 的图象有公共点,
则 ,解得 .
所以实数 的取值范围是 .
故答案为 .
【分析】 由对称性求函数解析式得:设y=f(x)的图象与y=g(x)的图象关于原点对称,由 , 得 , 利用导数研究函数的值域得:方程 在 有解,设对其求导结合导函数的性质即可得出函数的单调性,再数形结合法即可得出 , 从而求出a的取值范围。
14.在 的展开式中,若 ,则 ________.
【答案】 208
【考点】二项式系数的性质
【解析】【解答】 的展开式中含x的最高次项为 ,
的展开式中含x的最高次项为 ,
所以 展开式中含x的最高次项为 ,
所以 ,解得 ,
由已知得展开式中x的最高次为9,所以 , ;
的展开式中含 的项为 , 的展开式中含 的项为 ,
所以 ,
的展开式中含 的项为 , 的展开式中含 的项为 ,
所以 ,
所以 .
故答案为: 208.
【分析】 由题意结合二项式项的性质先求出n的值,由此可得m的值,再利用二项展开式的通项公式,求得的值即可.
15.酒杯的形状为倒立的圆锥(如图),杯深9cm,上口宽6 cm,水以 的流量倒入杯中,当水深为3cm时,水升高的瞬时变化率为________.
【答案】
【考点】变化的快慢与变化率,棱柱、棱锥、棱台的体积
【解析】【解答】由题意,设 时刻水面高为 ,水面圆半径为 , 则 可得
此时水的体积为
又由题设条件知,此时的水量为20t
故有 故有
当水深为3cm,对应的时间为 ,则
所以当水深为3 cm时,水升高的瞬时变化率为
故答案为:
【分析】根据题意作出如图的图象,建立起水面高h与时间t的函数关系,利用导数求出水面升高时的瞬时变化率即可.
16.若函数 的导函数 存在导数,记 的导数为 .如果对 x (a,b),都有 ,则 有如下性质: ,其中n , , ,…, (a,b).若 ,则 =________;在锐角△ABC中,根据上述性质推断:sinA+sinB+sinC的最大值为________.
【答案】 ;
【考点】正弦函数的图象,正弦函数的定义域和值域
【解析】【解答】解:设 , ,则 ,则 , ,
有如下性质: .
则 ,
的最大值为 ,
故答案为: , .
【分析】构造函数 , ,求导,则 ,由正弦函数的图象可知 成立,根据函数的性质 ,即可求得 的最大值.
四、解答题(共6题;共70分)
17.在下面两个条件中任选一个条件,补充在后面问题中的横线上,并完成解答.条件①:“展开式中所有项的系数之和与二项式系数之和的比为64”;条件②:“展开式中前三项的二项式系数之和为22”.
问题:已知二项式 ,若___________(填写条件前的序号),
(1)求展开式中系数最大的项;
(2)求 中含 项的系数.
【答案】 (1)若选条件①时,令 ,可得展开式所有项的系数和为 ,而二项式系数和为 ,
所以 ,解得 ,
若选条件②时,由前3项的二项式系数和为22可得 ,解得 .
设展开式中系数最大的项为第 项,则满足 ,
即 ,解得 ,又 ,
所以 ,
即展开式中系数最大的项为 ,
(2)在 中,含 项的系数为
.
【考点】组合及组合数公式,二项式系数的性质
【解析】【分析】 当选填条件①时,由题意列式求得n=6,当选填条件②时,由前3项的二项式系数和为22求得n=6.
(1)把n=6代入 , 可知第四项的二项式系数最大,由二项展开式的通项得答案;
(2)把n=6代入 , 由第一个因式的常数项乘以第二个因式含含×2项的系数,由第二个因式的常数项乘以第一个因式含含×2项的系数,第一个因式含有x项的系数乘以第二个因式含有x项的系数,最后求和得出答案.
18.用0,1,2,3,4,5这六个数字:(最后运算结果请以数字作答)
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的四位数?
(3)能组成多少个无重复数字且比1230大的四位数?
【答案】 (1)符合要求的四位偶数可分为三类:
第一类:0在个位时有 个;
第二类:2在个位时,首位从1,3,4,5中选定1个(有 种),十位和百位从余下的数字中选(有 种),于是有 个;
第三类:4在个位时,与第二类同理,也有 个.
由分类加法计数原理知,共有四位偶数: 个.
(2)符合要求的数可分为两类:个位数上的数字是0的四位数有 个;个位数上的数字是5的五位数有 个.故满足条件的五位数的个数共有 个.
(3)符合要求的比1230大的四位数可分为四类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共 个;
第二类:形如13□□,14□□,15□□,共有 个;
第三类:形如124□,125□,共有 个;
第四类:形如123□,共有 个
由分类加法计数原理知,无重复数字且比1230大的四位数共有: 个.
【考点】排列、组合及简单计数问题
【解析】【分析】 (1)根据题意,分情况讨论;当0在个位,2在个位,4在个位,再由分类计数原理可得;
(2)由题意看得出:5的倍数则个位数字为0或5的数,再根据分类计数原理可得;
(2)根据题意,分4种情况讨论,结合分类计数原理可得.
19.已知 展开式的二项式系数和为512,且
(1)求 的值;
(2)求 被6整除的余数.
【答案】 (1)因为 展开式的二项式系数和为 ,
所以 ,
故 .
令 ,可得 ,
令 ,可得 ,
即 ,
.
(2)
显然,展开式除了最后2项外,其余各项都能被6整除,
故展开式被6整出的余数,即 被6整除的余数为5.
【考点】二项式系数的性质,整除的概念和性质
【解析】【分析】 (1)由题意利用二项式系数的性质,求得n的值,再分别令x=1,x=2,计算出要求式子的值即可.
(2)根据题意把按照二项式定理展开,可得它除以6的余数.
20.已知 .
(1)当 时,求 在 上的最大值;
(2)当 时,讨论 的单调性.
【答案】 (1)解:当 时,
由 ,得 ,当 时解得 ,
所以 在 上单调递减,在 上单调递增,
所以最大值在端点处取得,
又
所以 在 上的最大值为 .
(2)当 时,
①当 时 ,得 ,得
在 上单调递增,在 上单调递减.
②当 时, ,
方程 的两根为 且
所以 ,得 ,得
即 在 上单调递增,在 上单调递减.
③当 时,
ⅰ.当 ,即 时, 在 上单调递增.
ⅱ. ,即 时
方程 的两根为 且
所以 ,得 或 ,所以 ,得
即 在 上单调递增,在 上单调递减
综上:
当 时, 在 上单调递增,在 上单调递减;
当 时, 在 上单调递增,在 上单调递减;
当 时, 在 上单调递增,在 上单调递减;
当 时, 在 上单调递增
【考点】函数单调性的性质,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
【解析】【分析】(1)由已知条件把a、b、c的值代入求出函数的解析式,再对其求导结合导函数的性质即可得出函数的单调性,利用函数的单调性即可求出最值。
(2)首先把b与c的值代入由此得出函数的解析式,再对其求导结合导函数的性质,对a分情况讨论即可得出函数的单调性。
21.已知函数 .
(1)求 过 的切线方程;
(2)若 在 上的最大值为 ,求证: .
【答案】 (1)解:设切点为 ,
∵ . , ,
∴切线方程为 ,
∵切线过点 , ,解得: ,
∴切线方程为 ;
(2)证明: , , .
.
, , .
函数 在 , 上单调递增,
又 , (1) ,
因此函数 在 , 上存在唯一零点 ,并且 , , (可得 .
当 当
时,函数 取得极大值即最大值
, .
而函数 在 上单调递减.
,
而 , ,
.
【考点】利用导数研究函数的单调性,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
【解析】【分析】(1)由已知条件首先对函数求导,再把点的坐标代入求出切线的斜率,结合点斜式即可求出直线的方程。
(2)根据题意对函数求导得出 , 构造函数由该函数的单调性即可求出零点的唯一性,再结合整理得出当时,函数g(x)的最值情况,再结合函数的单调性得出 , 由此得到。
22.已知函数 (其中e为自然对数的底数).
(1)求函数 的极值;
(2)当 时,若 恒成立,求实数b的取值范围.
【答案】 (1)由 得 , 当 时, 无极值;
当 时,令 ,得 ,
当 时 ,当 时 ,
函数 在 上单调递减;函数 在 单调递增.
∴ 函数 存在极小值.其极小值为 ,无极大值.
(2)由题意有 恒成立,即 恒成立,
设 ,
则 ,
设 ,下面证明 有唯一解.
易知 单调递增,且 ,所以若 有零点x,则 ,
令 ,可得 , (※)
注意到 ,
所以方程(※)等价于 ,
又由(1)可知,当 时, 在 上单调递增,
又当 时, ,
所以方程 等价于方程 ,
设函数 ,则 单调递增,
又 , ,所以存在 ,使得
,即方程 有唯一解 ,即 ,
因此方程 有唯一解 ,
所以 有唯一解 .
且当 时, , 单调递减;
当 时, , 单调递增;
所以 的最小值为 ,
所以 .
【考点】函数的最值及其几何意义,利用导数研究函数的单调性,利用导数研究函数的极值
【解析】【分析】(1)根据题意首先对其求导结合导函数的性质即可得出函数的单调性,再由函数的单调性得出函数的极值情况。
(2)由已知条件 恒成立,即 恒成立,构造函数对其求导结合导函数的性质即可得出函数的单调性,由函数的单调性即可求出函数的零点,结合题意
令 ,可得 , 由函数f(x)的单调性 所以方程 等价于方程 , 设函数结合该函数的单调性以及方程根的情况即可得出 有唯一解 再结合函数的单调性.即可求出函数g(x)的最小值。
一、单选题(共9题;共45分)
1.已知函数 的定义域为 ,导函数 在 内的图象如图所示,则函数 在 内的极大值有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.已知函数 的图象在(1,f(1))处的切线经过坐标原点,则函数y=f(x)的最小值为(??? )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?1
3.若函数 的极大值点与极大值分别为a , b , 则(??? )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
4.设函数 ,则 是(??? )
A.?奇函数,且在 上是增函数??????????????????????????B.?奇函数,且在 上是减函数
C.?偶函数,且在 上是增函数??????????????????????????D.?偶函数,且在 上是减函数
5.已知函数 的定义域为 ,其导函数是 .有 ,则关于x的不等式 的解集为(??? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
6.某校开展学农活动时进行劳动技能比赛,通过初选,选甲?乙?丙?丁?戊共5名同学进行决赛,决出第1名到第5名的名次.甲?乙?丙三人去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”;对丙说“甲比你好”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有(??? )
A.?24种????????????????????????????????????B.?16种????????????????????????????????????C.?18种????????????????????????????????????D.?20种
7.已知 ,则 (??? )
A.?-10????????????????????????????????????????B.?10????????????????????????????????????????C.?-45????????????????????????????????????????D.?45
8.埃及金字塔之谜是人类史上最大的谜,它的神奇远远超过了人类的想象.在埃及金字塔内有一组神秘的数字142857,因为 ,…,所以这组数字又叫“走马灯数”.该组数字还有如下发现: ,…,若从这组神秘数字中任选3个数字构成一个三位数x , 剩下的三个数字构成另一个三位数y , ,将所有可能的三位数x按从小到大依次排序,则第12个三位数x为(??? )
A.?214??????????????????????????????????????B.?215??????????????????????????????????????C.?248??????????????????????????????????????D.?284
9.我国古代著名的数学著作中,《周碑算经》?《九章算术》?《孙子算经》?《五曹算经》?《夏侯阳算经》?《孙丘建算经》?《海岛算经》?《五经算术》?《级术》和《纠古算经》,称为“算经十书”,某老师将其中的《周碑算经》?《九章算术》?《孙子算经》?《五经算术》?《级术》和《纠古算经》6本书分给4名数学爱好者,其中每人至少一本,则不同的分配方法的种数为(??? )
A.???????????B.???????????C.???????????D.?
二、多选题(共3题;共15分)
10.函数 的定义域为R , 它的导函数 的部分图象如图所示,则下面结论正确的是(??? )
A.?在 上函数 为增函数???????????????????????????B.?在 上函数 为增函数
C.?在 上函数 有极大值????????????????????????????D.? 是函数 在区间 上的极小值点
11.定义在R上的函数 ,其导函数 满足 ,则下列不等关系正确的是(??? )
A.??????????????B.??????????????C.??????????????D.?
12.已知 的二项展开式中系数之和为729,则下列结论正确的是(??? )
A.?二项展开式中各项二项式系数之和为 ??????????????B.?二项展开式中二项式系数最大的项为
C.?二项展开式中无常数项???????????????????????????????????????D.?二项展开式中系数最大的项为
三、填空题(共4题;共20分)
13.已知函数 与 的图像上存在关于原点对称的对称点,则实数a的取值范围是________.
14.在 的展开式中,若 ,则 ________.
15.酒杯的形状为倒立的圆锥(如图),杯深9cm,上口宽6 cm,水以 的流量倒入杯中,当水深为3cm时,水升高的瞬时变化率为________.
16.若函数 的导函数 存在导数,记 的导数为 .如果对 x (a,b),都有 ,则 有如下性质: ,其中n , , ,…, (a,b).若 ,则 =________;在锐角△ABC中,根据上述性质推断:sinA+sinB+sinC的最大值为________.
四、解答题(共6题;共70分)
17.在下面两个条件中任选一个条件,补充在后面问题中的横线上,并完成解答.条件①:“展开式中所有项的系数之和与二项式系数之和的比为64”;条件②:“展开式中前三项的二项式系数之和为22”.
问题:已知二项式 ,若___________(填写条件前的序号),
(1)求展开式中系数最大的项;
(2)求 中含 项的系数.
18.用0,1,2,3,4,5这六个数字:(最后运算结果请以数字作答)
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的四位数?
(3)能组成多少个无重复数字且比1230大的四位数?
19.已知 展开式的二项式系数和为512,且
(1)求 的值;
(2)求 被6整除的余数.
20.已知 .
(1)当 时,求 在 上的最大值;
(2)当 时,讨论 的单调性.
21.已知函数 .
(1)求 过 的切线方程;
(2)若 在 上的最大值为 ,求证: .
22.已知函数 (其中e为自然对数的底数).
(1)求函数 的极值;
(2)当 时,若 恒成立,求实数b的取值范围.
答案解析部分
一、单选题(共9题;共45分)
1.已知函数 的定义域为 ,导函数 在 内的图象如图所示,则函数 在 内的极大值有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
【答案】 B
【考点】利用导数研究函数的单调性,利用导数研究函数的极值
【解析】【解答】根据导数的图象,可知导数有4个零点,从左向右分析,
第一个零点与第四个零点左侧为正右侧为负,所以函数 先增后减,故第一个零点与第四个零点处函数 有极大值,第二个零点左侧为负右侧为正,故函数 先减后增,第二个零点处函数 有极小值,第三个零点两侧,导数值同为正,故该点不是极值点,
故答案为:B
【分析】 根据导函数的图象判断导数零点两侧的符号(先正后负),即可求解.
2.已知函数 的图象在(1,f(1))处的切线经过坐标原点,则函数y=f(x)的最小值为(??? )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?1
【答案】 C
【考点】导数的几何意义,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
【解析】【解答】函数 ,则 ,
且 ,所以 ,
所以 ,解得 ,
所以 ,( ),
,
令 ,即 ,解得 ,
令 ,即 ,解得 ,
所以函数在区间 上单调递减,在区间 上单调递增,
所以 。
故答案为:C
【分析】利用求导的方法切成函数在切点处的切线的斜率,再利用切点的横坐标求出切点的纵坐标,进而求出切点的坐标,再利用点斜式求出函数在切点处的切线方程,再利用切线经过坐标原点,结合代入法,进而求出a的值,从而求出函数的解析式,再利用求导的方法判断函数的单调性,再利用函数的单调性求出函数的最小值。
3.若函数 的极大值点与极大值分别为a , b , 则(??? )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
【答案】 C
【考点】利用导数研究函数的单调性,利用导数研究函数的极值
【解析】【解答】∵ ,
∴ 或 ,
, 或 ,
∴ 在 单调递增,在 单调递减,
∴ 为极大值点,且 ,
∴ , ,
∴ ,
故答案为:C.
【分析】 先对函数求导,然后结合导数分析函数的单调性,进而可求函数的极大值与极大值点,从而可求.
4.设函数 ,则 是(??? )
A.?奇函数,且在 上是增函数??????????????????????????B.?奇函数,且在 上是减函数
C.?偶函数,且在 上是增函数??????????????????????????D.?偶函数,且在 上是减函数
【答案】 A
【考点】复合函数的单调性,函数奇偶性的判断,奇偶性与单调性的综合
【解析】【解答】 ? 的定义域为
而 ,所以 为奇函数;
在 上, ,
因为 在 上为增函数 在 上为减函数,
所以 在 上是增函数
故答案为:A.
【分析】 根据题意先检验f(-x)与f(x)的关系,然后结合复合函数单调性及奇偶性的定义进行检验即可判断.
5.已知函数 的定义域为 ,其导函数是 .有 ,则关于x的不等式 的解集为(??? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
【答案】 B
【考点】函数单调性的性质,利用导数研究函数的单调性
【解析】【解答】由题意,函数 满足 ,
令 ,则
函数 是定义域 内的单调递减函数,
由于 ,关于 的不等式 可化为 ,
即 ,所以 且 ,解得 ,
不等式 的解集为 .
故答案为:B
【分析】 根据题意令 , 求导,结合题意可得g(x)在上单调递减;而得到从而可得答案.
6.某校开展学农活动时进行劳动技能比赛,通过初选,选甲?乙?丙?丁?戊共5名同学进行决赛,决出第1名到第5名的名次.甲?乙?丙三人去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”;对丙说“甲比你好”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有(??? )
A.?24种????????????????????????????????????B.?16种????????????????????????????????????C.?18种????????????????????????????????????D.?20种
【答案】 C
【考点】排列、组合及简单计数问题
【解析】【解答】由题意可得,第1名不可能是甲?乙?丙,只能是丁或戊;第5名不可能是甲乙,只能是丙或丁或戊;因此可分如下三种情况:
若甲是第2名,先考虑乙,则有 种情况,再考虑丙,则有 种情况,最后排丁?戊,则有 种情况,即此时所包含的情况有: 种;
若甲是第3名,当乙是第4名时,丙只能是第5名,只需考虑丁?戊的排列,此时有 种情况;当乙是第2名时,丙可以有 种选择,最后排丁?戊,则有 种情况;此时包含的情况共有 种;
若甲是第4名,则丙是第5名,而乙有 种选择,最后排丁?戊,则有 种情况,;此时所包含的情况有 ;
综上,从这个回答中分析这5人的名次排列顺序可能出现的种类有 种.
故答案为:C.
【分析】 根据题意可得甲乙不是最后一名或第一名,根据排列组合以及分类计数原理计算出结果即可。
7.已知 ,则 (??? )
A.?-10????????????????????????????????????????B.?10????????????????????????????????????????C.?-45????????????????????????????????????????D.?45
【答案】 D
【考点】二项式系数的性质
【解析】【解答】
, .
故答案为:D
【分析】利用二项式的通项公式,结合已知条件代入数值计算出结果即可。
8.埃及金字塔之谜是人类史上最大的谜,它的神奇远远超过了人类的想象.在埃及金字塔内有一组神秘的数字142857,因为 ,…,所以这组数字又叫“走马灯数”.该组数字还有如下发现: ,…,若从这组神秘数字中任选3个数字构成一个三位数x , 剩下的三个数字构成另一个三位数y , ,将所有可能的三位数x按从小到大依次排序,则第12个三位数x为(??? )
A.?214??????????????????????????????????????B.?215??????????????????????????????????????C.?248??????????????????????????????????????D.?284
【答案】 C
【考点】排列、组合及简单计数问题
【解析】【解答】∵1,4,7,2,8,5,这六个数中,1+8=9,2+7=9,4+5=9,共3组
要使六个数字中任意取出3个数字构成一个三位数 ,剩下的三个数字构成另一个三位数 ,且 ,所以 从小到大排列为: ,故第12个三位数x为248.
故答案为:C
【分析】 根据题意,在数字142857中,两个数字之和为9的组合有3个,据此依次分析数字x、y的百位、十位、个位数字的情况,即可求出.
9.我国古代著名的数学著作中,《周碑算经》?《九章算术》?《孙子算经》?《五曹算经》?《夏侯阳算经》?《孙丘建算经》?《海岛算经》?《五经算术》?《级术》和《纠古算经》,称为“算经十书”,某老师将其中的《周碑算经》?《九章算术》?《孙子算经》?《五经算术》?《级术》和《纠古算经》6本书分给4名数学爱好者,其中每人至少一本,则不同的分配方法的种数为(??? )
A.???????????B.???????????C.???????????D.?
【答案】 B
【考点】列举法计算基本事件数及事件发生的概率,排列、组合及简单计数问题
【解析】【解答】根据题意,第一类,从6本书中取出3本视作一本书,连同剩余的3本分配给4个人,共有 种分法,
第二类,从6本书中取出2本书,再从剩余4本书中取出2本书,平均分堆后连同剩余2本,视作4本书分配给4个人,共有 ,
由分类加法计数原理可得,不同的分配方法的种数为 ,
故答案为:B
【分析】根据题意6本分给4名数学爱好者,每人至少一本,则把6本书为6本书为(3,1,11)和(2,2,1,1),再分配给4名数学爱好者, 再由概率的定义代入数值计算出结果即可。
二、多选题(共3题;共15分)
10.函数 的定义域为R , 它的导函数 的部分图象如图所示,则下面结论正确的是(??? )
A.?在 上函数 为增函数???????????????????????????B.?在 上函数 为增函数
C.?在 上函数 有极大值????????????????????????????D.? 是函数 在区间 上的极小值点
【答案】 A,C
【考点】函数的图象,利用导数研究函数的单调性,函数在某点取得极值的条件
【解析】【解答】由图象可知 在区间 和 上 , 递增;在区间 上 , 递减.
所以A选项正确,B选项错误.
在区间 上, 有极大值为 ,C选项正确.
在区间 上, 是 的极小值点,D选项错误.
故答案为:AC
【分析】由已知条件,结合图象即可得出导函数的性质,由此得出函数的单调性,利用函数的单调性即可求出函数的极值,对选项逐一判断即可得出答案。
11.定义在R上的函数 ,其导函数 满足 ,则下列不等关系正确的是(??? )
A.??????????????B.??????????????C.??????????????D.?
【答案】 A,B,D
【考点】函数单调性的性质,利用导数研究函数的单调性
【解析】【解答】令 ,则 ,
, 在 上恒成立,
在 上单调递增,
对A, ,A符合题意;
对B, ,B符合题意;
对C, ,C不符合题意;
对D, ,D符合题意;
故答案为:ABD.
【分析】根据题意构造函数 , 并对其求导结合导函数的性质即可得出函数的单调性,由函数的单调性对选项逐一判断即可得出答案。
12.已知 的二项展开式中系数之和为729,则下列结论正确的是(??? )
A.?二项展开式中各项二项式系数之和为 ??????????????B.?二项展开式中二项式系数最大的项为
C.?二项展开式中无常数项???????????????????????????????????????D.?二项展开式中系数最大的项为
【答案】 A,B
【考点】二项式定理,二项式系数的性质
【解析】【解答】令 ,则 二项展开式系数和为 ,解得: ;
展开式的通项公式为 ;
对于A,由 知其二项式系数和为 ,A符合题意;
对于B,当 时,二项式系数最大,则所求项为 ,B符合题意;
对于C,令 ,解得: ,则展开式第5项为常数项,C不符合题意;
对于D,分别令 ,可得展开式为 ,由此可确定系数最大的项为 ,D不符合题意.
故答案为:AB.
【分析】 由题意利用二项展开式的通项公式,再结合二项式系数的性质,对选项逐一判断即可得出答案。
三、填空题(共4题;共20分)
13.已知函数 与 的图像上存在关于原点对称的对称点,则实数a的取值范围是________.
【答案】
【考点】函数的值域,奇偶函数图象的对称性,利用导数研究函数的单调性
【解析】【解答】函数 与 的图像上存在关于原点对称的对称点,
∴方程 ,即 在 上有解,
∴方程 在 有解.
设 , ,且 为 的切线,
设切点为 ,
由 得 ,
则有 ,解得 .
由图象可得,要使直线 和 的图象有公共点,
则 ,解得 .
所以实数 的取值范围是 .
故答案为 .
【分析】 由对称性求函数解析式得:设y=f(x)的图象与y=g(x)的图象关于原点对称,由 , 得 , 利用导数研究函数的值域得:方程 在 有解,设对其求导结合导函数的性质即可得出函数的单调性,再数形结合法即可得出 , 从而求出a的取值范围。
14.在 的展开式中,若 ,则 ________.
【答案】 208
【考点】二项式系数的性质
【解析】【解答】 的展开式中含x的最高次项为 ,
的展开式中含x的最高次项为 ,
所以 展开式中含x的最高次项为 ,
所以 ,解得 ,
由已知得展开式中x的最高次为9,所以 , ;
的展开式中含 的项为 , 的展开式中含 的项为 ,
所以 ,
的展开式中含 的项为 , 的展开式中含 的项为 ,
所以 ,
所以 .
故答案为: 208.
【分析】 由题意结合二项式项的性质先求出n的值,由此可得m的值,再利用二项展开式的通项公式,求得的值即可.
15.酒杯的形状为倒立的圆锥(如图),杯深9cm,上口宽6 cm,水以 的流量倒入杯中,当水深为3cm时,水升高的瞬时变化率为________.
【答案】
【考点】变化的快慢与变化率,棱柱、棱锥、棱台的体积
【解析】【解答】由题意,设 时刻水面高为 ,水面圆半径为 , 则 可得
此时水的体积为
又由题设条件知,此时的水量为20t
故有 故有
当水深为3cm,对应的时间为 ,则
所以当水深为3 cm时,水升高的瞬时变化率为
故答案为:
【分析】根据题意作出如图的图象,建立起水面高h与时间t的函数关系,利用导数求出水面升高时的瞬时变化率即可.
16.若函数 的导函数 存在导数,记 的导数为 .如果对 x (a,b),都有 ,则 有如下性质: ,其中n , , ,…, (a,b).若 ,则 =________;在锐角△ABC中,根据上述性质推断:sinA+sinB+sinC的最大值为________.
【答案】 ;
【考点】正弦函数的图象,正弦函数的定义域和值域
【解析】【解答】解:设 , ,则 ,则 , ,
有如下性质: .
则 ,
的最大值为 ,
故答案为: , .
【分析】构造函数 , ,求导,则 ,由正弦函数的图象可知 成立,根据函数的性质 ,即可求得 的最大值.
四、解答题(共6题;共70分)
17.在下面两个条件中任选一个条件,补充在后面问题中的横线上,并完成解答.条件①:“展开式中所有项的系数之和与二项式系数之和的比为64”;条件②:“展开式中前三项的二项式系数之和为22”.
问题:已知二项式 ,若___________(填写条件前的序号),
(1)求展开式中系数最大的项;
(2)求 中含 项的系数.
【答案】 (1)若选条件①时,令 ,可得展开式所有项的系数和为 ,而二项式系数和为 ,
所以 ,解得 ,
若选条件②时,由前3项的二项式系数和为22可得 ,解得 .
设展开式中系数最大的项为第 项,则满足 ,
即 ,解得 ,又 ,
所以 ,
即展开式中系数最大的项为 ,
(2)在 中,含 项的系数为
.
【考点】组合及组合数公式,二项式系数的性质
【解析】【分析】 当选填条件①时,由题意列式求得n=6,当选填条件②时,由前3项的二项式系数和为22求得n=6.
(1)把n=6代入 , 可知第四项的二项式系数最大,由二项展开式的通项得答案;
(2)把n=6代入 , 由第一个因式的常数项乘以第二个因式含含×2项的系数,由第二个因式的常数项乘以第一个因式含含×2项的系数,第一个因式含有x项的系数乘以第二个因式含有x项的系数,最后求和得出答案.
18.用0,1,2,3,4,5这六个数字:(最后运算结果请以数字作答)
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的四位数?
(3)能组成多少个无重复数字且比1230大的四位数?
【答案】 (1)符合要求的四位偶数可分为三类:
第一类:0在个位时有 个;
第二类:2在个位时,首位从1,3,4,5中选定1个(有 种),十位和百位从余下的数字中选(有 种),于是有 个;
第三类:4在个位时,与第二类同理,也有 个.
由分类加法计数原理知,共有四位偶数: 个.
(2)符合要求的数可分为两类:个位数上的数字是0的四位数有 个;个位数上的数字是5的五位数有 个.故满足条件的五位数的个数共有 个.
(3)符合要求的比1230大的四位数可分为四类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共 个;
第二类:形如13□□,14□□,15□□,共有 个;
第三类:形如124□,125□,共有 个;
第四类:形如123□,共有 个
由分类加法计数原理知,无重复数字且比1230大的四位数共有: 个.
【考点】排列、组合及简单计数问题
【解析】【分析】 (1)根据题意,分情况讨论;当0在个位,2在个位,4在个位,再由分类计数原理可得;
(2)由题意看得出:5的倍数则个位数字为0或5的数,再根据分类计数原理可得;
(2)根据题意,分4种情况讨论,结合分类计数原理可得.
19.已知 展开式的二项式系数和为512,且
(1)求 的值;
(2)求 被6整除的余数.
【答案】 (1)因为 展开式的二项式系数和为 ,
所以 ,
故 .
令 ,可得 ,
令 ,可得 ,
即 ,
.
(2)
显然,展开式除了最后2项外,其余各项都能被6整除,
故展开式被6整出的余数,即 被6整除的余数为5.
【考点】二项式系数的性质,整除的概念和性质
【解析】【分析】 (1)由题意利用二项式系数的性质,求得n的值,再分别令x=1,x=2,计算出要求式子的值即可.
(2)根据题意把按照二项式定理展开,可得它除以6的余数.
20.已知 .
(1)当 时,求 在 上的最大值;
(2)当 时,讨论 的单调性.
【答案】 (1)解:当 时,
由 ,得 ,当 时解得 ,
所以 在 上单调递减,在 上单调递增,
所以最大值在端点处取得,
又
所以 在 上的最大值为 .
(2)当 时,
①当 时 ,得 ,得
在 上单调递增,在 上单调递减.
②当 时, ,
方程 的两根为 且
所以 ,得 ,得
即 在 上单调递增,在 上单调递减.
③当 时,
ⅰ.当 ,即 时, 在 上单调递增.
ⅱ. ,即 时
方程 的两根为 且
所以 ,得 或 ,所以 ,得
即 在 上单调递增,在 上单调递减
综上:
当 时, 在 上单调递增,在 上单调递减;
当 时, 在 上单调递增,在 上单调递减;
当 时, 在 上单调递增,在 上单调递减;
当 时, 在 上单调递增
【考点】函数单调性的性质,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
【解析】【分析】(1)由已知条件把a、b、c的值代入求出函数的解析式,再对其求导结合导函数的性质即可得出函数的单调性,利用函数的单调性即可求出最值。
(2)首先把b与c的值代入由此得出函数的解析式,再对其求导结合导函数的性质,对a分情况讨论即可得出函数的单调性。
21.已知函数 .
(1)求 过 的切线方程;
(2)若 在 上的最大值为 ,求证: .
【答案】 (1)解:设切点为 ,
∵ . , ,
∴切线方程为 ,
∵切线过点 , ,解得: ,
∴切线方程为 ;
(2)证明: , , .
.
, , .
函数 在 , 上单调递增,
又 , (1) ,
因此函数 在 , 上存在唯一零点 ,并且 , , (可得 .
当 当
时,函数 取得极大值即最大值
, .
而函数 在 上单调递减.
,
而 , ,
.
【考点】利用导数研究函数的单调性,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
【解析】【分析】(1)由已知条件首先对函数求导,再把点的坐标代入求出切线的斜率,结合点斜式即可求出直线的方程。
(2)根据题意对函数求导得出 , 构造函数由该函数的单调性即可求出零点的唯一性,再结合整理得出当时,函数g(x)的最值情况,再结合函数的单调性得出 , 由此得到。
22.已知函数 (其中e为自然对数的底数).
(1)求函数 的极值;
(2)当 时,若 恒成立,求实数b的取值范围.
【答案】 (1)由 得 , 当 时, 无极值;
当 时,令 ,得 ,
当 时 ,当 时 ,
函数 在 上单调递减;函数 在 单调递增.
∴ 函数 存在极小值.其极小值为 ,无极大值.
(2)由题意有 恒成立,即 恒成立,
设 ,
则 ,
设 ,下面证明 有唯一解.
易知 单调递增,且 ,所以若 有零点x,则 ,
令 ,可得 , (※)
注意到 ,
所以方程(※)等价于 ,
又由(1)可知,当 时, 在 上单调递增,
又当 时, ,
所以方程 等价于方程 ,
设函数 ,则 单调递增,
又 , ,所以存在 ,使得
,即方程 有唯一解 ,即 ,
因此方程 有唯一解 ,
所以 有唯一解 .
且当 时, , 单调递减;
当 时, , 单调递增;
所以 的最小值为 ,
所以 .
【考点】函数的最值及其几何意义,利用导数研究函数的单调性,利用导数研究函数的极值
【解析】【分析】(1)根据题意首先对其求导结合导函数的性质即可得出函数的单调性,再由函数的单调性得出函数的极值情况。
(2)由已知条件 恒成立,即 恒成立,构造函数对其求导结合导函数的性质即可得出函数的单调性,由函数的单调性即可求出函数的零点,结合题意
令 ,可得 , 由函数f(x)的单调性 所以方程 等价于方程 , 设函数结合该函数的单调性以及方程根的情况即可得出 有唯一解 再结合函数的单调性.即可求出函数g(x)的最小值。
同课章节目录
