2020—2021学年北师大版数学九年级下册1.4解直角三角形课时练习(word版含答案)
文档属性
| 名称 | 2020—2021学年北师大版数学九年级下册1.4解直角三角形课时练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 118.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 10:08:17 | ||
图片预览

文档简介
北师大版数学九年级下册
1.4《解直角三角形》课时练习
一、选择题
1.如图,在△ABC中,∠C=90°,AB=15,sinB=0.6,则AC等于( )
A.3 B.9 C.4 D.12
2.在△ABC中,AB=5,BC=6,∠B为锐角且sinB=,则∠C的正弦值等于( )
A. B. C. D.
3.如图,在△ABC中,∠BAC=90°,AD⊥BC于D, DC=4,BC=9,则AC为( )
A.5 B.6 C.7 D.8
4.如图,在四边形ABCD中,AD//BC,AC⊥AB,AD=CD,cos∠DCA=0.8,BC=10,则AB值是(?? )
A.3 B.6 C.8 D.9
5.如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为( )
A.2 B.4 C.8 D.8
6.如图,在直角坐标平面内,点P与原点O的距离OP=3,线段OP与X轴正半轴的夹角为a,且cosα=, 则点P的坐标是(????).
A.(2,3) B.(2,) C.(, 2) D.(2,)
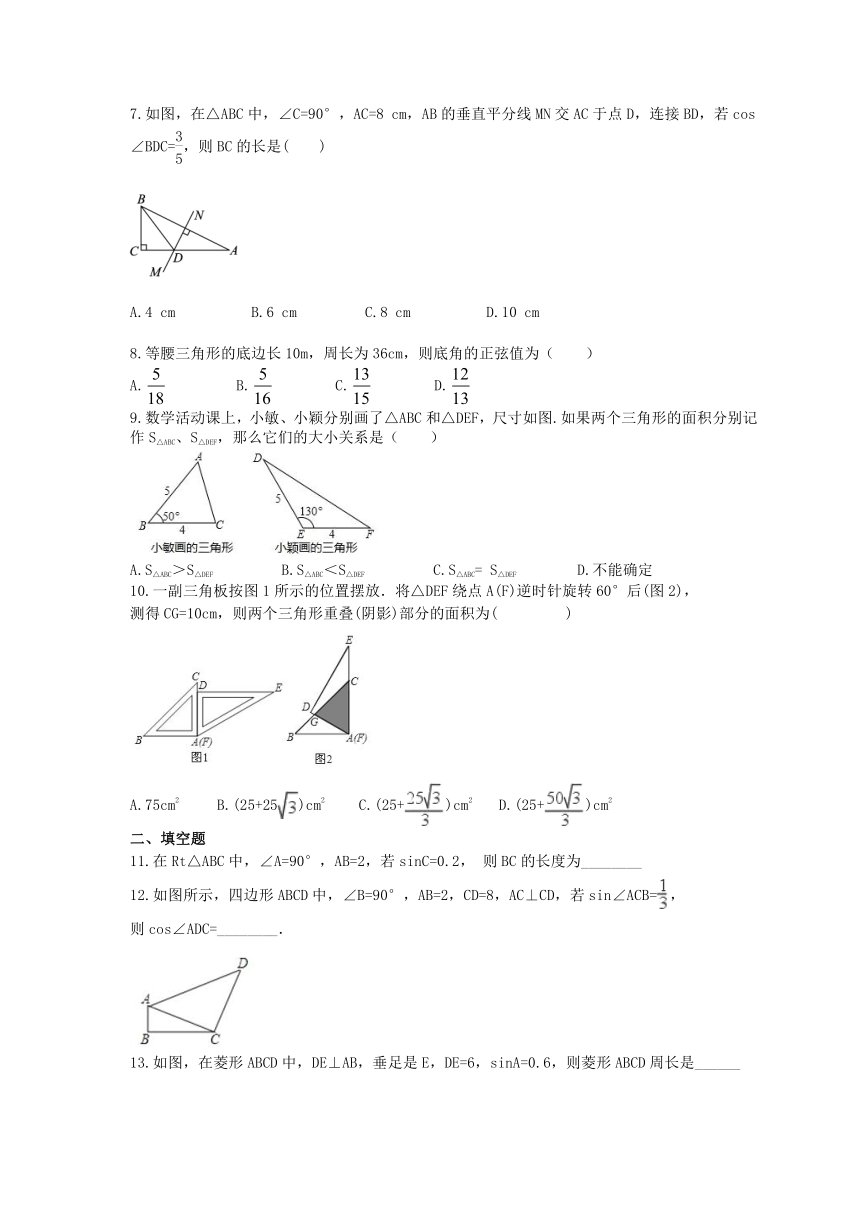
7.如图,在△ABC中,∠C=90°,AC=8 cm,AB的垂直平分线MN交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
A.4 cm B.6 cm C.8 cm D.10 cm
8.等腰三角形的底边长10m,周长为36cm,则底角的正弦值为( )
A. B. C. D.
9.数学活动课上,小敏、小颖分别画了△ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作S△ABC、S△DEF,那么它们的大小关系是( )
A.S△ABC>S△DEF B.S△ABC<S△DEF C.S△ABC= S△DEF D.不能确定
10.一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),
测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( ? ?? )
A.75cm2 B.(25+25)cm2 C.(25+)cm2 D.(25+)cm2
二、填空题
11.在Rt△ABC中,∠A=90°,AB=2,若sinC=0.2, 则BC的长度为________?
12.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,
则cos∠ADC=________.
13.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA=0.6,则菱形ABCD周长是______
14.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=0.2,
则AD的长为______
三、解答题
15.如图,在△ABC中,AC=2,∠A=45°,tanB=0.5,求BC的长.
16.如图,矩形ABCD的对角线AC.BD相交于点O, 过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值 .
?
参考答案
1.B
2.C
3.B.
4.B.
5.B.
6.D.
7.A.
8.D
9.C
10.C.
11.答案为:10
12.答案为:0.8
13.答案为: 40
14.答案为:2
15.解:如图,过点C作CD⊥AB于D,
∵AC=2,∠A=45°,
∴CD=AC?sin∠A=2?sin45°=2×=
∵tanB= ,∴BD=CD
tanB =
∴BC=
16.解:连接EC,
∵四边形ABCD为矩形,
∴OA=OC , ∠ABC=90°,
利用勾股定理得:AC=10,即OA=5,
∵OE⊥AC,
∴AE=CE,
在Rt△EDC中,设EC=AE=x, 则有ED=AD-AE=8-x, DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x= ,
∴AE= ,
在Rt△AOE中,sin∠OEA= .
1.4《解直角三角形》课时练习
一、选择题
1.如图,在△ABC中,∠C=90°,AB=15,sinB=0.6,则AC等于( )
A.3 B.9 C.4 D.12
2.在△ABC中,AB=5,BC=6,∠B为锐角且sinB=,则∠C的正弦值等于( )
A. B. C. D.
3.如图,在△ABC中,∠BAC=90°,AD⊥BC于D, DC=4,BC=9,则AC为( )
A.5 B.6 C.7 D.8
4.如图,在四边形ABCD中,AD//BC,AC⊥AB,AD=CD,cos∠DCA=0.8,BC=10,则AB值是(?? )
A.3 B.6 C.8 D.9
5.如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为( )
A.2 B.4 C.8 D.8
6.如图,在直角坐标平面内,点P与原点O的距离OP=3,线段OP与X轴正半轴的夹角为a,且cosα=, 则点P的坐标是(????).
A.(2,3) B.(2,) C.(, 2) D.(2,)
7.如图,在△ABC中,∠C=90°,AC=8 cm,AB的垂直平分线MN交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
A.4 cm B.6 cm C.8 cm D.10 cm
8.等腰三角形的底边长10m,周长为36cm,则底角的正弦值为( )
A. B. C. D.
9.数学活动课上,小敏、小颖分别画了△ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作S△ABC、S△DEF,那么它们的大小关系是( )
A.S△ABC>S△DEF B.S△ABC<S△DEF C.S△ABC= S△DEF D.不能确定
10.一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),
测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( ? ?? )
A.75cm2 B.(25+25)cm2 C.(25+)cm2 D.(25+)cm2
二、填空题
11.在Rt△ABC中,∠A=90°,AB=2,若sinC=0.2, 则BC的长度为________?
12.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,
则cos∠ADC=________.
13.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA=0.6,则菱形ABCD周长是______
14.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=0.2,
则AD的长为______
三、解答题
15.如图,在△ABC中,AC=2,∠A=45°,tanB=0.5,求BC的长.
16.如图,矩形ABCD的对角线AC.BD相交于点O, 过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值 .
?
参考答案
1.B
2.C
3.B.
4.B.
5.B.
6.D.
7.A.
8.D
9.C
10.C.
11.答案为:10
12.答案为:0.8
13.答案为: 40
14.答案为:2
15.解:如图,过点C作CD⊥AB于D,
∵AC=2,∠A=45°,
∴CD=AC?sin∠A=2?sin45°=2×=
∵tanB= ,∴BD=CD
tanB =
∴BC=
16.解:连接EC,
∵四边形ABCD为矩形,
∴OA=OC , ∠ABC=90°,
利用勾股定理得:AC=10,即OA=5,
∵OE⊥AC,
∴AE=CE,
在Rt△EDC中,设EC=AE=x, 则有ED=AD-AE=8-x, DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x= ,
∴AE= ,
在Rt△AOE中,sin∠OEA= .
