五年级下册数学课件-2.1 正数和负数 沪教版(12页PPT)
文档属性
| 名称 | 五年级下册数学课件-2.1 正数和负数 沪教版(12页PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 15:04:21 | ||
图片预览




文档简介
(共12张PPT)
正数、负数的加减法
人们在生活中经常会遇到各种相反意义的量。比如,在记账时有余有亏;在计算粮仓存米时,有时要记进粮食,有时要记出粮食。为了方便,人们就考虑了相反意义的数来表示。于是人们引入了正负数这个概念,把余钱进粮食记为正,把亏钱、出粮食记为负。可见正负数是生产实践中产生的。
据史料记载,早在两千多年前,中国就有了正负数的概念,掌握了正负数的运算法则。
中国三国时期的学者刘徽在建立负数的概念上有重大贡献。刘徽首先给出了正负数的定义,他说:“今两算得失相反,要令正负以名之。”意思是说,在计算过程中遇到具有相反意义的量,要用正数和负数来区分它。
中国在《九章算术》《方程》章中就引入了负数(negative
number)的概念和正负数加减法的运算法则。在某些问题中,以卖出的数目为正(因是收入),买入的数目为负(因是付款);余钱为正,不足钱为负。在关于粮谷计算中,则以加进去的为正,减掉的为负。“正”、“负”这一对术语从这时起一直沿用到现在。正负数的乘除法则出现得比较晚,在1299
年朱世杰编写的《算学启蒙》中,《明正负术》一项讲了正负数加减法法则,一共八条,比《九章算术》更加明确。在“明乘除段”中有“同名相乘为正,异名相乘为负”之句,也就是(±a)×(±b)=+ab,(±a)×(
b)=-ab,这样的正负数乘法法则,是中国最早的记载。
印度人最早在中国之后提出负数,628年左右的婆罗摩笈多(约598-665)。他提出了负数的运算法则,并用小点或小圈记在数字上表示负数。在欧洲初步认识提出负数概念,最早要算意大利数学家斐波那契(1170-1250)。他在解决一个盈利问题时说︰我将证明这个问题不可能有解,除非承认这个人可以负债。15世纪的舒开(1445?-1510?)和16世纪的史提非(1553)虽然他们都发现了负数,但又都把负数说成是荒谬的数,卡当(1545)给出了方程的负根,但他把它说成是“假数”。韦达知道负数的存在,但他完全不要负数。笛卡儿部分地接受了负数,他把方程的负根叫假根,因它比“无/零”更小。
哈雷奥特(1560-1621)偶然地把负数单独地写在方程的一边,并用“-”表示它们,但他并不接受负数。邦别利(1526-1572)给出了负数的明确定义。史提文在方程里用了正、负系数,并接受了负根。基拉德(1595-1629)把负数与正数等量齐观、并用减号“-”表示负数。总之在16、17世纪,欧洲人虽然接触了负数,但对负数的接受的进展是缓慢的。
画一画、说一说?
你能根据题意画出示意图吗?
(1)、某人向东走5米,再向东走3米,两次一共走了多少米?
(2)、某人向西走5米,再向西走3米,两次一共向东走了多少米?
根据所列算式你还可以编哪些情境?
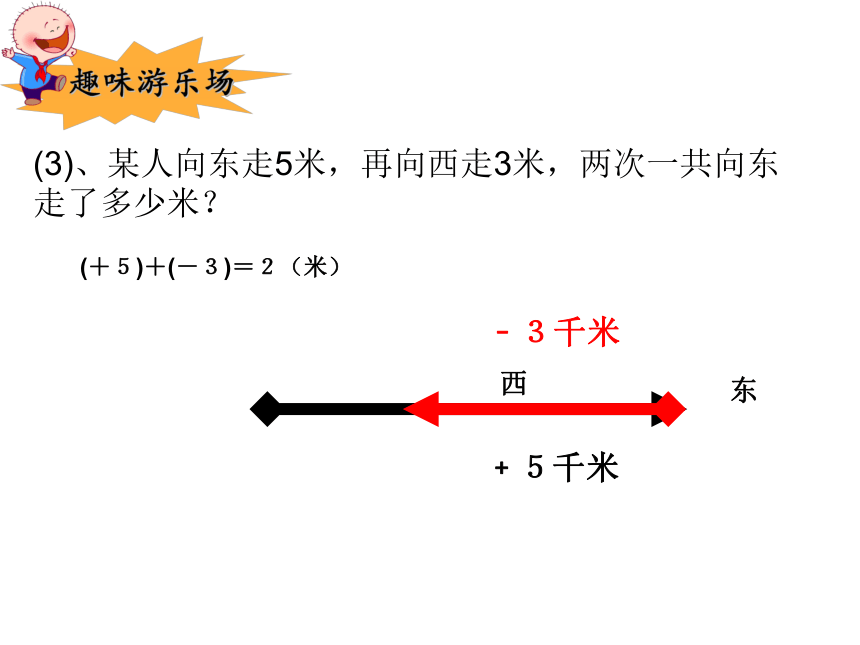
(3)、某人向东走5米,再向西走3米,两次一共向东走了多少米?
(+5)+(-3)=2(米)
东
西
﹢5千米
﹣3千米
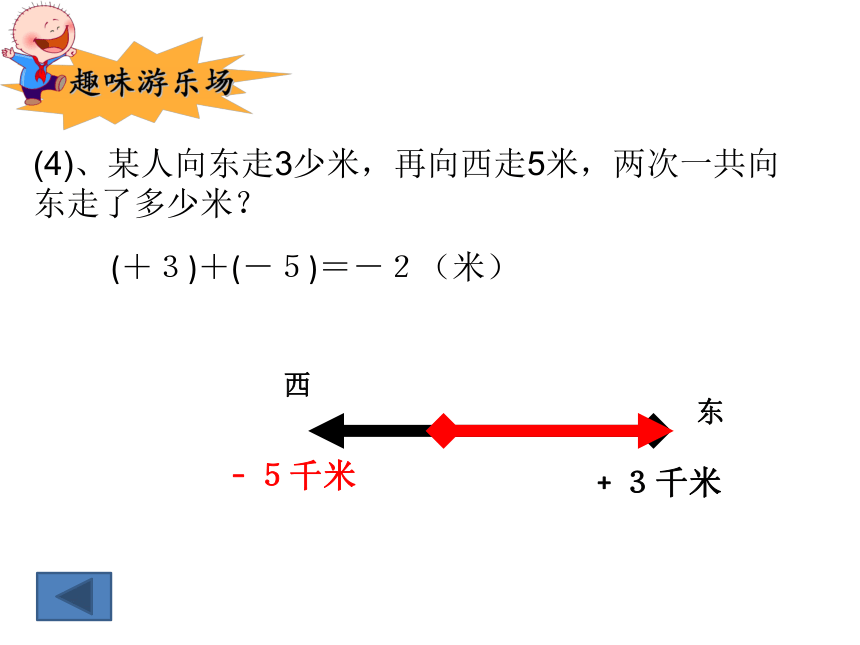
(4)、某人向东走3少米,再向西走5米,两次一共向东走了多少米?
(+3)+(-5)=-2(米)
东
西
﹢3千米
﹣5千米
欢乐探究谷
你能根据算式画出示意图吗?根据所列算式你还可以编哪些情境?
(1)2×3
其中2看作向东运动2米;×3看作沿此
方向运动3次
结果是向东运动了6米,所以有2×3=6
.
(2)(-2)×3
其中-2看作向西运动2米;×3看作沿此
方向运动3次
,如图所示.
结果是向西运动了6米,所以有(-2)×3=-6.
欢乐探究谷
(3)2×(-3)
结果是向西运动了6米,所以有2×(-3)=-6.
其中2看作向东运动2米;×(-3)看
作沿相反方向运动3次
.
欢乐探究谷
(4)(-2)×(-3)
其中-2看作向西运动2米,×(-3)
看作沿与此方向相反的方向运动了3次,
即:向东运动了3次,共向东运动了6米,
所以有(-2)×(-3)=6.
欢乐探究谷
从确定下列积的符号,你能从中发现什么?
你能找出生活中正、负数加减法和乘除法的运用吗?
正数、负数的加减法
人们在生活中经常会遇到各种相反意义的量。比如,在记账时有余有亏;在计算粮仓存米时,有时要记进粮食,有时要记出粮食。为了方便,人们就考虑了相反意义的数来表示。于是人们引入了正负数这个概念,把余钱进粮食记为正,把亏钱、出粮食记为负。可见正负数是生产实践中产生的。
据史料记载,早在两千多年前,中国就有了正负数的概念,掌握了正负数的运算法则。
中国三国时期的学者刘徽在建立负数的概念上有重大贡献。刘徽首先给出了正负数的定义,他说:“今两算得失相反,要令正负以名之。”意思是说,在计算过程中遇到具有相反意义的量,要用正数和负数来区分它。
中国在《九章算术》《方程》章中就引入了负数(negative
number)的概念和正负数加减法的运算法则。在某些问题中,以卖出的数目为正(因是收入),买入的数目为负(因是付款);余钱为正,不足钱为负。在关于粮谷计算中,则以加进去的为正,减掉的为负。“正”、“负”这一对术语从这时起一直沿用到现在。正负数的乘除法则出现得比较晚,在1299
年朱世杰编写的《算学启蒙》中,《明正负术》一项讲了正负数加减法法则,一共八条,比《九章算术》更加明确。在“明乘除段”中有“同名相乘为正,异名相乘为负”之句,也就是(±a)×(±b)=+ab,(±a)×(
b)=-ab,这样的正负数乘法法则,是中国最早的记载。
印度人最早在中国之后提出负数,628年左右的婆罗摩笈多(约598-665)。他提出了负数的运算法则,并用小点或小圈记在数字上表示负数。在欧洲初步认识提出负数概念,最早要算意大利数学家斐波那契(1170-1250)。他在解决一个盈利问题时说︰我将证明这个问题不可能有解,除非承认这个人可以负债。15世纪的舒开(1445?-1510?)和16世纪的史提非(1553)虽然他们都发现了负数,但又都把负数说成是荒谬的数,卡当(1545)给出了方程的负根,但他把它说成是“假数”。韦达知道负数的存在,但他完全不要负数。笛卡儿部分地接受了负数,他把方程的负根叫假根,因它比“无/零”更小。
哈雷奥特(1560-1621)偶然地把负数单独地写在方程的一边,并用“-”表示它们,但他并不接受负数。邦别利(1526-1572)给出了负数的明确定义。史提文在方程里用了正、负系数,并接受了负根。基拉德(1595-1629)把负数与正数等量齐观、并用减号“-”表示负数。总之在16、17世纪,欧洲人虽然接触了负数,但对负数的接受的进展是缓慢的。
画一画、说一说?
你能根据题意画出示意图吗?
(1)、某人向东走5米,再向东走3米,两次一共走了多少米?
(2)、某人向西走5米,再向西走3米,两次一共向东走了多少米?
根据所列算式你还可以编哪些情境?
(3)、某人向东走5米,再向西走3米,两次一共向东走了多少米?
(+5)+(-3)=2(米)
东
西
﹢5千米
﹣3千米
(4)、某人向东走3少米,再向西走5米,两次一共向东走了多少米?
(+3)+(-5)=-2(米)
东
西
﹢3千米
﹣5千米
欢乐探究谷
你能根据算式画出示意图吗?根据所列算式你还可以编哪些情境?
(1)2×3
其中2看作向东运动2米;×3看作沿此
方向运动3次
结果是向东运动了6米,所以有2×3=6
.
(2)(-2)×3
其中-2看作向西运动2米;×3看作沿此
方向运动3次
,如图所示.
结果是向西运动了6米,所以有(-2)×3=-6.
欢乐探究谷
(3)2×(-3)
结果是向西运动了6米,所以有2×(-3)=-6.
其中2看作向东运动2米;×(-3)看
作沿相反方向运动3次
.
欢乐探究谷
(4)(-2)×(-3)
其中-2看作向西运动2米,×(-3)
看作沿与此方向相反的方向运动了3次,
即:向东运动了3次,共向东运动了6米,
所以有(-2)×(-3)=6.
欢乐探究谷
从确定下列积的符号,你能从中发现什么?
你能找出生活中正、负数加减法和乘除法的运用吗?
