湖南省名校联考联合体2020-2021学年高一下学期6月大联考数学试题 Word版含解析
文档属性
| 名称 | 湖南省名校联考联合体2020-2021学年高一下学期6月大联考数学试题 Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 09:48:45 | ||
图片预览




文档简介
湖南省名校联考联合体2021年春季高一大联考
数 学
时量:120分钟 满分:150分
得分:________
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合false,false,则“false”是“false”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
2.函数false的零点所在的一个区间是( )
A.(1,2) B.(2,3) C.(3,4) D.(4,5)
3.已知false,则false( )
A.false B.false C.false D.false
4.已知平面直角坐标系xOy中,原点为O,点false,false,C(3,0),则向量false在向量false方向上的投影向量为( )
A.false B.false C.false D.false
5.已知false,false,false,则( )
A.false B.false C.false D.false
6.已知直三棱柱false的6个顶点都在球O的球面上,若false,false,false,false,则球O的表面积为( )
A.false B.false C.false D.false
7.我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若false,false,false,则false( )
A.false B.false
C.false D.false
8.已知函数false,且false,则( )
A.false B.false
C.false D.false
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.若复数false满足false(i为虚数单位),则下列结论正确的有( )
A.z的虚部为false B.false
C.z的共轭复数为false D.z是第三象限的点
10.设平面向量false,false,false均为非零向量,则下列命题中正确的是( )
A.若false,则false
B.若false,则false与false共线
C.若false,则false
D.已知false,false且false与false的夹角为锐角,则实数false的取值范围是false
11.在false中,角A、B、C的对边分别为a、b、c,则下列结论中正确的是( )
A.在false中,若false,则false
B.若false,则false是等腰三角形
C.若false,则false是直角三角形
D.若false,则false是锐角三角形
12.意大利画家列奥纳多·达·芬奇(1452.4—1519.5)的画作《抱银貂的女人》中,女士脖颈上悬挂的黑色珍珠项链与主人相互映衬呈现出不一样的美与光泽,达·芬奇提出固定项链的两端,使其在重力的作用下自然下垂,项链所形成的曲线是什么?这就是著名的“悬链线问题”,后人给出了悬链线的函数解析式:false,其中a为悬链线系数,false称为双曲余弦函数,其表达式为false,相应地,双曲正弦函数的函数表达式为false.则下列关于双曲正、余弦函数结论中正确的是( )
A.false
B.false
C.false
D.false为偶函数,且存在最小值
三、填空题:本题共4小题,每小题5分,共20分.
13.若函数false为偶函数,则false的一个值为________.(写出一个即可)
14.已知向量false,false,若false,则false________.
15.1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式false,这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥” .根据此公式,则false________;false________.(第一空2分,第二空3分)
16.在false中,false为钝角,false,false且false,函数false的最小值为false,则false的最小值为________.
四、解答题:本题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
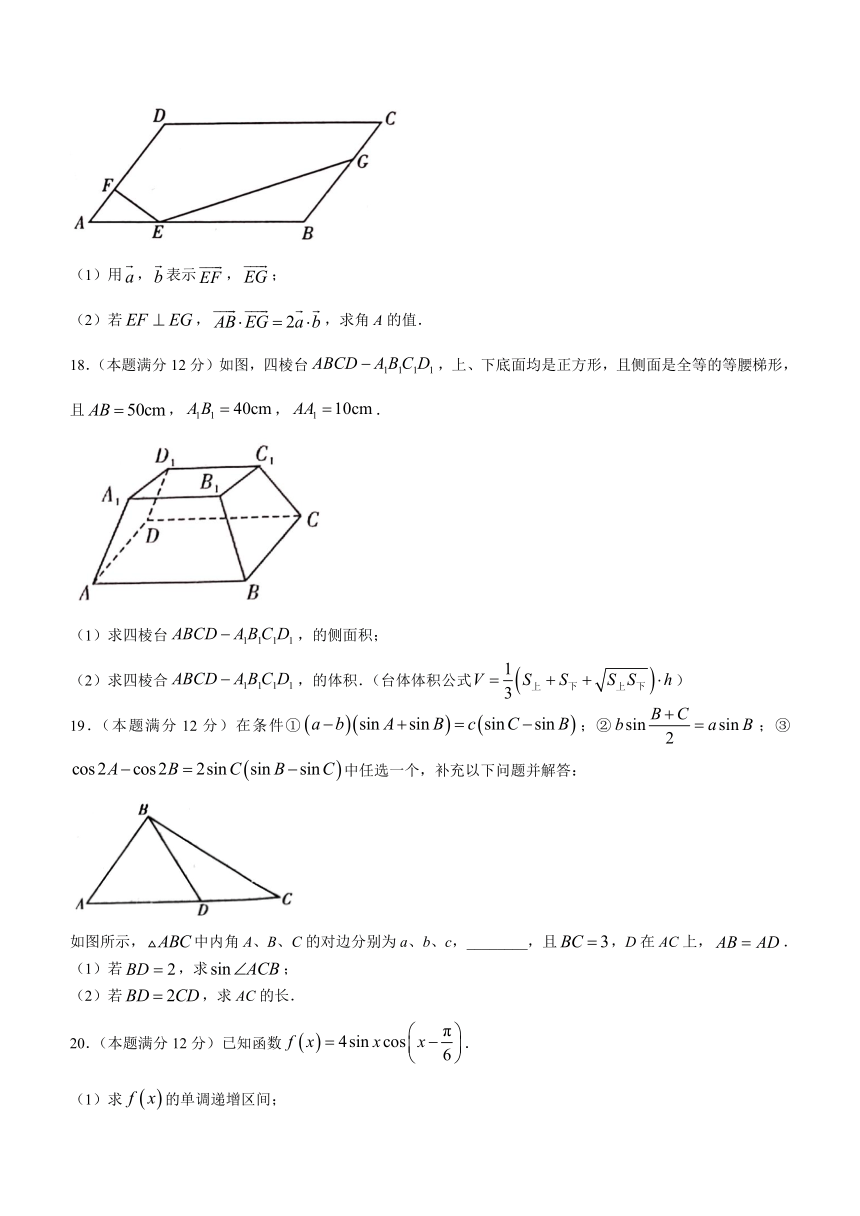
17.(本题满分10分)如图,在平行四边形ABCD中,点E、F、G分别在边AB、AD、BC上,且满足false,false,false,设false,false.
(1)用false,false表示false,false;
(2)若false,false,求角A的值.
18.(本题满分12分)如图,四棱台false,上、下底面均是正方形,且侧面是全等的等腰梯形,且false,false,false.
(1)求四棱台false,的侧面积;
(2)求四棱合false,的体积.(台体体积公式false)
19.(本题满分12分)在条件①false;②false;③false中任选一个,补充以下问题并解答:
如图所示,false中内角A、B、C的对边分别为a、b、c,________,且false,D在AC上,false.
(1)若false,求false;
(2)若false,求AC的长.
20.(本题满分12分)已知函数false.
(1)求false的单调递增区间;
(2)在false中,角A、B、C的对边分别为a、b、c.若false,false,求false面积的最大值.
21.(本题满分12分)今年,我国某一企业为了进一步增加市场竞争力,计划在2021年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万元,每生产x(千部)手机,需另投入成本false万元,且false由市场调研知,海部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(1)求出2021年的利润false(万元)关于年产量x(千部)的函数关系式(利润false销售额false成本);
(2)2021年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
22.(本题满分12分)已如函数false,false.
(1)若函数false是奇函数,求实数a的值;
(2)在(1)的条件下,判断函数false与函数false的图象公共点个数,并说明理由;
(3)当false时,函数false的图象始终在函数false的图象上方,求实数false的取值范围.
名校联考联合体2021年春季高一大联考
数学参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
题号
1
2
3
4
5
6
7
8
答案
C
B
B
A
A
C
B
A
1.C 【解析】false,false,则false,即“false”是“false”的必要不充分条件.
2.B 【解析】函数false在false上单调递增且连续,且falsefalse,false;故函数false的零点所在的一个区间是(2,3).
3.B 【解析】由false,得false,则false.
4.A 【解析】false,false,向量false在向量false方向上的投影向量为false.
5.A 【解析】∵false,false,falsefalse,∴false.
6.C 【解析】由题意,三棱柱false为直三棱柱false,底面ABC为直角三角形,把直三棱柱false补成回棱柱,则四棱柱的体对角线是其外接球的直径,所以外接球半径为false,则三棱柱false外接球的表面积是false.
7.B 【解析】法一:过F作false于G,不坊设false,false,则false,false,所以false,false,false,所以false,false,所以falsefalse.
法二:false,即false,解得false,即false.
法三:建立直角坐标系用坐标解决.
8.A 【解析】令false,则false,false是奇函数,且易知false在R上递增,则false在R上递增,又false,故false,故false,false.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
题号
9
10
11
12
答案
BC
BC
AC
ACD
9.BC 【解析】∵false,∴false,虚部为false,false,共轭复数为false,z是第四象限的点.
10.BC 【解析】当false,false在false方向上的投影相同时,显然false不一定成立,A错误;若false,则向量夹角false或false,false与false同向或反向,共线,B正确;若false,两边平方得,false,即false,C正确;若false与false的夹角为锐角,则false,且false,所以D不正确.
11.AC 【解析】在false中,若false,根据大边对大角,所以false,利用正弦定理,所以false,则false,故选项A正确;对于选项B,∵false,∴false或false,,即false或false,false为等腰或直角三角形,即选项B错误;对于选项C,由余弦定理知,falsefalse,化简整理得false,∴false为直角三角形,即选项C正确,(也可以化边为角);对于选项D,false只能说明C为锐角,而角A和B不确定,即选项D错误.
12.ACD 【解析】对于A.false,故A正确;对于B.falsefalse,故B错误;对于C,false,故C正确;对于D.false,故函数为偶函数,由于false,故false(当且仅当false时,等号成立),故D正确.
三、填空题:本题共4小题,每小题5分,共20分.
13.false(答案不唯一) 【解析】∵函数false为偶函数,∴false,false,故可取false.
14.false 【解析】因为向量false,false,且false,所以false,即false,所以false.
5.0;false 【解析】false,false,因此,false.
16.false 【解析】法一:由向量减法模的几何意义和函数false的最小值为false知false,且O点在直线AB上,当false时,false最小,为false.
法二:在false中,false为钝角,false,函数false的最小值为false.
∴函数false,
化为false恒成立.
当且仅当false时等号成立,代入得到false,∴false.
∴falsefalse,
当且仅当false时,false取得最小值false,
∴false的最小值为false.
四、解答题:本题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.【解析】(1)false,
false.4分
(2)若false,则false,
即false,∴false,6分
又false,
∴false,8分
∴false,即false,
∴false.10分
18.【解析】(1)∵侧面是全等的等腰梯形,false,false,false,
∴斜高为false,3分
则四棱台false的侧面积为false;6分
(2)∵侧面是全等的等腰梯形,false,false,false,
∴四棱台的高为false,9分
四棱台的体积为false.12分
19.【解析】选①false,
由正弦定理得,false,
整理得,false,由余弦定理得:false,
由A为三角形内角得,false;3分
选②false,
由false得,false
因为false,所以false,即false,由于false,
所以false,即false,故false;
选③false,
所以false,整理得,false,
由正弦定理得,false,由余弦定理得,false,
由A为三角形内角得,false;
(1)因为false,false,且false,
所以false为等边三角形,
所以false,false,false,
false中,由正弦定理得,false,
即false,
所以false,6分
(2)设false,则false,false,
false中,由余弦定理得,false,
故false,false.12分
20.【解析】(1)函数false
false,
令false,求得false,false,
可得函数的单调递增区间为false,false.6分
(2)在false中,若false,∴false,∴false.
∴false面积为false.
∵false,根据余弦定理可得false,
∴false,
∴false面积为false,
故false面积的最大值为false.
21.【解析】(1)当false时,false,2分
当false时,false,4分
∴false5分
(2)若false,false,
当false时,false万元,7分
若false,false,9分
当且仅当false时,即false时,false万元,11分
∴2021年产量为100(千部)时,企业所获利润最大,最大利润是9000万元.12分
22.【解析】(1)函数false为奇函数,
所以对于定义域内任意x,都有false,即false,
∴false,
显然false,由于奇函数定义域关于原点对称,所以必有false.
上面等式左右两边同时乘以false得false,
化简得false,上式对定义域内任意x恒成立,
所以必有false,解得false;3分
(2)由(1)如false,所以false,即false,
由false,得false或false,
所以函数false定义域false,
由题意,要求方程false解的个数,
即求方程false在定义域D上的解的个数.
令false,显然false在区间false和false均单调递增,
又false,false.
且false,false,
所以函数false在区间false和false上各有一个零点,
即方程false在定义域D上有2个解,
所以函数false与函数false的图象有2个公共点;7分
(3)要使false时,函数false的图象始终在函数false的图象的上方,
必须使false在false上恒成立,
令false,则false,上式整理得false在false恒成立.
因为false在false恒成立,即false.
又false,所以得false在false恒成立,
令false,则false,且false,
所以false,
由基本不等式可知false(当且仅当false时,等号成立)
即false,
所以false,
所以a的取值范围是false.12分
数 学
时量:120分钟 满分:150分
得分:________
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合false,false,则“false”是“false”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
2.函数false的零点所在的一个区间是( )
A.(1,2) B.(2,3) C.(3,4) D.(4,5)
3.已知false,则false( )
A.false B.false C.false D.false
4.已知平面直角坐标系xOy中,原点为O,点false,false,C(3,0),则向量false在向量false方向上的投影向量为( )
A.false B.false C.false D.false
5.已知false,false,false,则( )
A.false B.false C.false D.false
6.已知直三棱柱false的6个顶点都在球O的球面上,若false,false,false,false,则球O的表面积为( )
A.false B.false C.false D.false
7.我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若false,false,false,则false( )
A.false B.false
C.false D.false
8.已知函数false,且false,则( )
A.false B.false
C.false D.false
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.若复数false满足false(i为虚数单位),则下列结论正确的有( )
A.z的虚部为false B.false
C.z的共轭复数为false D.z是第三象限的点
10.设平面向量false,false,false均为非零向量,则下列命题中正确的是( )
A.若false,则false
B.若false,则false与false共线
C.若false,则false
D.已知false,false且false与false的夹角为锐角,则实数false的取值范围是false
11.在false中,角A、B、C的对边分别为a、b、c,则下列结论中正确的是( )
A.在false中,若false,则false
B.若false,则false是等腰三角形
C.若false,则false是直角三角形
D.若false,则false是锐角三角形
12.意大利画家列奥纳多·达·芬奇(1452.4—1519.5)的画作《抱银貂的女人》中,女士脖颈上悬挂的黑色珍珠项链与主人相互映衬呈现出不一样的美与光泽,达·芬奇提出固定项链的两端,使其在重力的作用下自然下垂,项链所形成的曲线是什么?这就是著名的“悬链线问题”,后人给出了悬链线的函数解析式:false,其中a为悬链线系数,false称为双曲余弦函数,其表达式为false,相应地,双曲正弦函数的函数表达式为false.则下列关于双曲正、余弦函数结论中正确的是( )
A.false
B.false
C.false
D.false为偶函数,且存在最小值
三、填空题:本题共4小题,每小题5分,共20分.
13.若函数false为偶函数,则false的一个值为________.(写出一个即可)
14.已知向量false,false,若false,则false________.
15.1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式false,这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥” .根据此公式,则false________;false________.(第一空2分,第二空3分)
16.在false中,false为钝角,false,false且false,函数false的最小值为false,则false的最小值为________.
四、解答题:本题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本题满分10分)如图,在平行四边形ABCD中,点E、F、G分别在边AB、AD、BC上,且满足false,false,false,设false,false.
(1)用false,false表示false,false;
(2)若false,false,求角A的值.
18.(本题满分12分)如图,四棱台false,上、下底面均是正方形,且侧面是全等的等腰梯形,且false,false,false.
(1)求四棱台false,的侧面积;
(2)求四棱合false,的体积.(台体体积公式false)
19.(本题满分12分)在条件①false;②false;③false中任选一个,补充以下问题并解答:
如图所示,false中内角A、B、C的对边分别为a、b、c,________,且false,D在AC上,false.
(1)若false,求false;
(2)若false,求AC的长.
20.(本题满分12分)已知函数false.
(1)求false的单调递增区间;
(2)在false中,角A、B、C的对边分别为a、b、c.若false,false,求false面积的最大值.
21.(本题满分12分)今年,我国某一企业为了进一步增加市场竞争力,计划在2021年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万元,每生产x(千部)手机,需另投入成本false万元,且false由市场调研知,海部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(1)求出2021年的利润false(万元)关于年产量x(千部)的函数关系式(利润false销售额false成本);
(2)2021年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
22.(本题满分12分)已如函数false,false.
(1)若函数false是奇函数,求实数a的值;
(2)在(1)的条件下,判断函数false与函数false的图象公共点个数,并说明理由;
(3)当false时,函数false的图象始终在函数false的图象上方,求实数false的取值范围.
名校联考联合体2021年春季高一大联考
数学参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
题号
1
2
3
4
5
6
7
8
答案
C
B
B
A
A
C
B
A
1.C 【解析】false,false,则false,即“false”是“false”的必要不充分条件.
2.B 【解析】函数false在false上单调递增且连续,且falsefalse,false;故函数false的零点所在的一个区间是(2,3).
3.B 【解析】由false,得false,则false.
4.A 【解析】false,false,向量false在向量false方向上的投影向量为false.
5.A 【解析】∵false,false,falsefalse,∴false.
6.C 【解析】由题意,三棱柱false为直三棱柱false,底面ABC为直角三角形,把直三棱柱false补成回棱柱,则四棱柱的体对角线是其外接球的直径,所以外接球半径为false,则三棱柱false外接球的表面积是false.
7.B 【解析】法一:过F作false于G,不坊设false,false,则false,false,所以false,false,false,所以false,false,所以falsefalse.
法二:false,即false,解得false,即false.
法三:建立直角坐标系用坐标解决.
8.A 【解析】令false,则false,false是奇函数,且易知false在R上递增,则false在R上递增,又false,故false,故false,false.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
题号
9
10
11
12
答案
BC
BC
AC
ACD
9.BC 【解析】∵false,∴false,虚部为false,false,共轭复数为false,z是第四象限的点.
10.BC 【解析】当false,false在false方向上的投影相同时,显然false不一定成立,A错误;若false,则向量夹角false或false,false与false同向或反向,共线,B正确;若false,两边平方得,false,即false,C正确;若false与false的夹角为锐角,则false,且false,所以D不正确.
11.AC 【解析】在false中,若false,根据大边对大角,所以false,利用正弦定理,所以false,则false,故选项A正确;对于选项B,∵false,∴false或false,,即false或false,false为等腰或直角三角形,即选项B错误;对于选项C,由余弦定理知,falsefalse,化简整理得false,∴false为直角三角形,即选项C正确,(也可以化边为角);对于选项D,false只能说明C为锐角,而角A和B不确定,即选项D错误.
12.ACD 【解析】对于A.false,故A正确;对于B.falsefalse,故B错误;对于C,false,故C正确;对于D.false,故函数为偶函数,由于false,故false(当且仅当false时,等号成立),故D正确.
三、填空题:本题共4小题,每小题5分,共20分.
13.false(答案不唯一) 【解析】∵函数false为偶函数,∴false,false,故可取false.
14.false 【解析】因为向量false,false,且false,所以false,即false,所以false.
5.0;false 【解析】false,false,因此,false.
16.false 【解析】法一:由向量减法模的几何意义和函数false的最小值为false知false,且O点在直线AB上,当false时,false最小,为false.
法二:在false中,false为钝角,false,函数false的最小值为false.
∴函数false,
化为false恒成立.
当且仅当false时等号成立,代入得到false,∴false.
∴falsefalse,
当且仅当false时,false取得最小值false,
∴false的最小值为false.
四、解答题:本题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.【解析】(1)false,
false.4分
(2)若false,则false,
即false,∴false,6分
又false,
∴false,8分
∴false,即false,
∴false.10分
18.【解析】(1)∵侧面是全等的等腰梯形,false,false,false,
∴斜高为false,3分
则四棱台false的侧面积为false;6分
(2)∵侧面是全等的等腰梯形,false,false,false,
∴四棱台的高为false,9分
四棱台的体积为false.12分
19.【解析】选①false,
由正弦定理得,false,
整理得,false,由余弦定理得:false,
由A为三角形内角得,false;3分
选②false,
由false得,false
因为false,所以false,即false,由于false,
所以false,即false,故false;
选③false,
所以false,整理得,false,
由正弦定理得,false,由余弦定理得,false,
由A为三角形内角得,false;
(1)因为false,false,且false,
所以false为等边三角形,
所以false,false,false,
false中,由正弦定理得,false,
即false,
所以false,6分
(2)设false,则false,false,
false中,由余弦定理得,false,
故false,false.12分
20.【解析】(1)函数false
false,
令false,求得false,false,
可得函数的单调递增区间为false,false.6分
(2)在false中,若false,∴false,∴false.
∴false面积为false.
∵false,根据余弦定理可得false,
∴false,
∴false面积为false,
故false面积的最大值为false.
21.【解析】(1)当false时,false,2分
当false时,false,4分
∴false5分
(2)若false,false,
当false时,false万元,7分
若false,false,9分
当且仅当false时,即false时,false万元,11分
∴2021年产量为100(千部)时,企业所获利润最大,最大利润是9000万元.12分
22.【解析】(1)函数false为奇函数,
所以对于定义域内任意x,都有false,即false,
∴false,
显然false,由于奇函数定义域关于原点对称,所以必有false.
上面等式左右两边同时乘以false得false,
化简得false,上式对定义域内任意x恒成立,
所以必有false,解得false;3分
(2)由(1)如false,所以false,即false,
由false,得false或false,
所以函数false定义域false,
由题意,要求方程false解的个数,
即求方程false在定义域D上的解的个数.
令false,显然false在区间false和false均单调递增,
又false,false.
且false,false,
所以函数false在区间false和false上各有一个零点,
即方程false在定义域D上有2个解,
所以函数false与函数false的图象有2个公共点;7分
(3)要使false时,函数false的图象始终在函数false的图象的上方,
必须使false在false上恒成立,
令false,则false,上式整理得false在false恒成立.
因为false在false恒成立,即false.
又false,所以得false在false恒成立,
令false,则false,且false,
所以false,
由基本不等式可知false(当且仅当false时,等号成立)
即false,
所以false,
所以a的取值范围是false.12分
同课章节目录
