2021年浙江省中考数学三轮复习冲刺压轴题最后猜想:二次函数(Word版含答案)
文档属性
| 名称 | 2021年浙江省中考数学三轮复习冲刺压轴题最后猜想:二次函数(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 367.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 13:49:18 | ||
图片预览



文档简介
2021年浙江省中考数学三轮冲刺压轴题最后猜想:二次函数
一、选择题
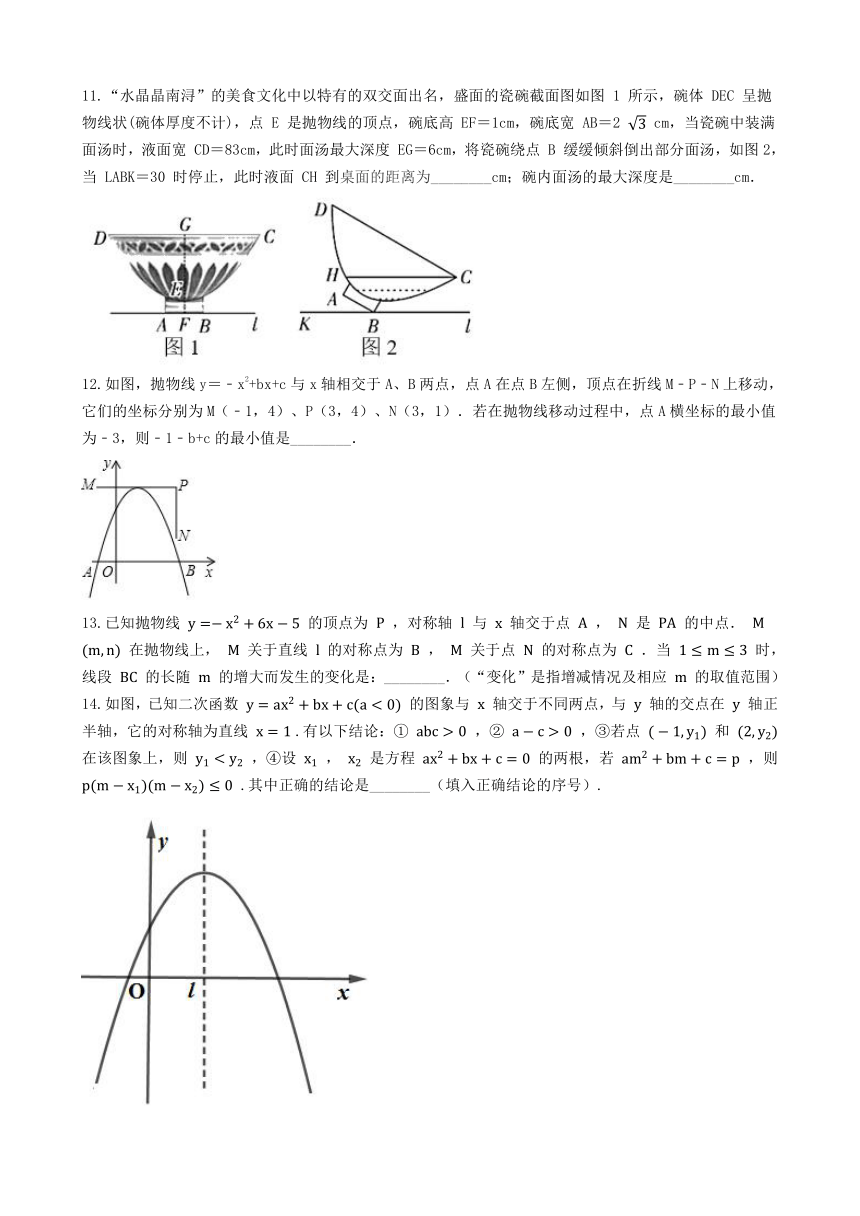
1.二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①abc>0;②4a+2b+c>0;③5a﹣b+c=0;④若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2
,
且x1<x2
,
则﹣5<x1<x2<1;⑤若方程|ax2+bx+c|=2有四个根,则这四个根的和为﹣4.其中正确的结论有(??
)
A.?2个??????????????????????B.?3个??????????????????C.?4个????????????????????????D.?5个
2.如图,二次函数
的图象如图所示,下列结论:①
;②
;③一元二次方程
有两个不相等的实数根;④当
或
时,
.上述结论中正确的个数是(???
)
A.?1个????????????????????B.?2个????????????????C.?3个????????????????????????????D.?4个
3.抛物线
(a
,
b
,
c为常数,且
)经过点
和
,且
,当
时,y随着x的增大而减小,有下列结论:①
;②若点
,点
都在抛物线上,则
;③
.其中,正确结论的个数为(???
)
A.?0??????????????????B.?1?????????????????????????C.?2??????????????????????????D.?3
4.已知当
时,二次函数
的值恒大于1,则k的取值范围是(??
)
A.?k≥
??????????B.?-
≤k≤-
????????C.?-
<k<0?????????D.?-
≤k<0
5.如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是(??
)
A.?不变??????B.?一直变大?????????C.?先减小后增大????????????D.?先增大后减小
6.二次函数
,当
且
时,y的最小值为
,最大值为
,则
的值为(????
)
A.????????????????????B.???????????????????C.????????????????????D.?
7.已知抛物线y=ax2+bx+c(a<0)的对称轴为x=-1,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有(??
)
A.?2个?????????????B.?3个???????????????C.?4个????????????????D.?5个
8.已知二次函数y=a(x-2)2+c,当x=
x1时,函数值为y1;当x=
x2时,函数值为y2.若|x1-2|>|x2-2|,下列表达式中正确的是(????
)
A.?y1+y2>0??????B.?y1-y2>0?????????C.?a(y1-y2)>0???????D.?a(y1+y2)>0
二、填空题
9.在平面直角坐标系xOy中,抛物线y=-x2+6x-8与x轴交于点A
,
B(点A在点B的左侧),与y轴交于点C
.
垂直于y轴的直线l与抛物线交于点P(x1
,
y1),Q(x2
,
y2),与直线BC交于点N(x3
,
y3),若x1,
记s=x1+x2+x3
,
则s的取值范围为________.
10.如图,一段抛物线:
,记为
,它与x轴交于两点O,
;将
绕
旋转
得到
,交x轴于
;将
绕
旋转
得到
,交x轴于
,过抛物线
,
顶点的直线与
、
、
围成的如图中的阴影部分,那么该阴影部分的面积为________.
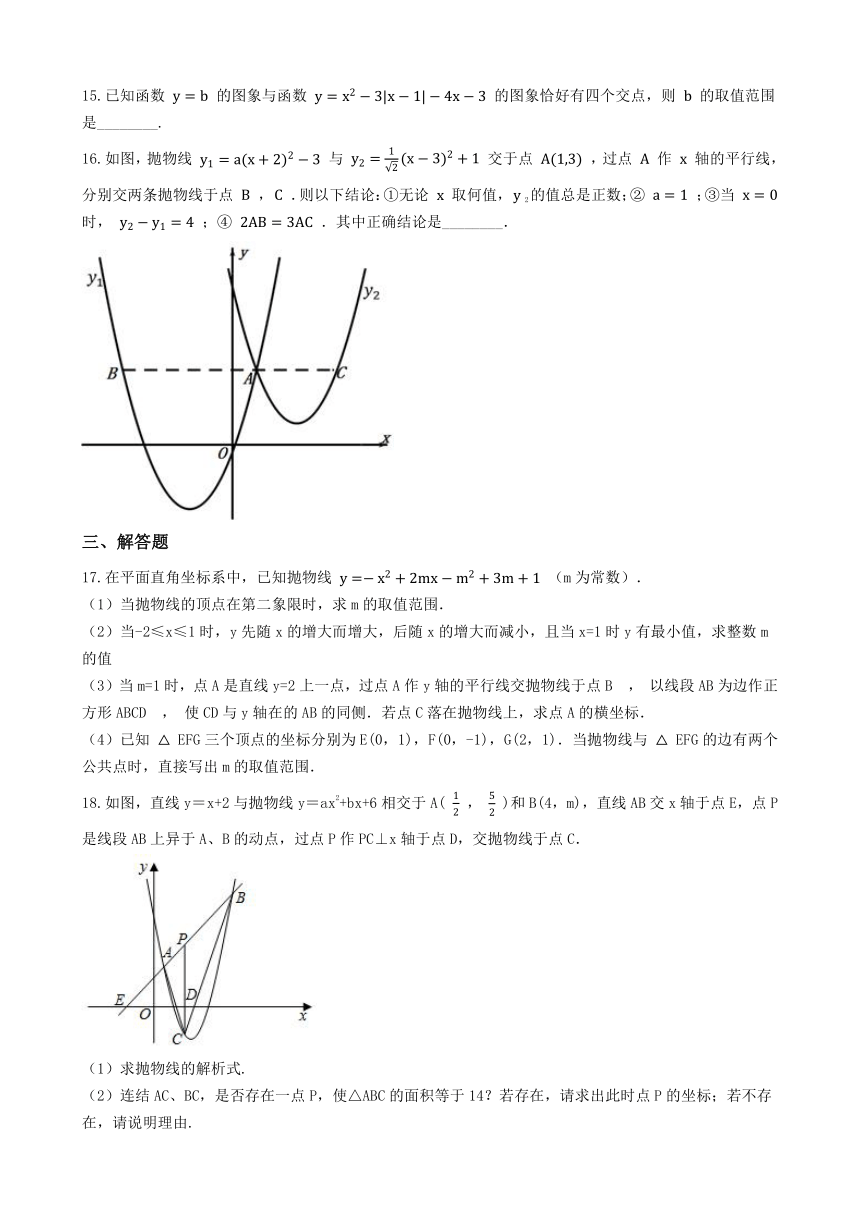
11.“水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图
1
所示,碗体
DEC
呈抛物线状(碗体厚度不计),点
E
是抛物线的顶点,碗底高
EF=1cm,碗底宽
AB=2
cm,当瓷碗中装满面汤时,液面宽
CD=83cm,此时面汤最大深度
EG=6cm,将瓷碗绕点
B
缓缓倾斜倒出部分面汤,如图2,当
LABK=30
时停止,此时液面
CH
到桌面的距离为________cm;碗内面汤的最大深度是________cm.
12.如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则﹣1﹣b+c的最小值是________.
13.已知抛物线
的顶点为
,对称轴
与
轴交于点
,
是
的中点.
在抛物线上,
关于直线
的对称点为
,
关于点
的对称点为
.当
时,线段
的长随
的增大而发生的变化是:________.(“变化”是指增减情况及相应
的取值范围)
14.如图,已知二次函数
的图象与
轴交于不同两点,与
轴的交点在
轴正半轴,它的对称轴为直线
.有以下结论:①
,②
,③若点
和
在该图象上,则
,④设
,
是方程
的两根,若
,则
.其中正确的结论是________(填入正确结论的序号).
15.已知函数
的图象与函数
的图象恰好有四个交点,则
的取值范围是________.
16.如图,抛物线
与
交于点
,过点
作
轴的平行线,分别交两条抛物线于点
,
.则以下结论:①无论
取何值,
2的值总是正数;②
;③当
时,
;④
.其中正确结论是________.
三、解答题
17.在平面直角坐标系中,已知抛物线
(m为常数).
(1)当抛物线的顶点在第二象限时,求m的取值范围.
(2)当-2≤x≤1时,y先随x的增大而增大,后随x的增大而减小,且当x=1时y有最小值,求整数m的值
(3)当m=1时,点A是直线y=2上一点,过点A作y轴的平行线交抛物线于点B
,
以线段AB为边作正方形ABCD
,
使CD与y轴在的AB的同侧.若点C落在抛物线上,求点A的横坐标.
(4)已知
EFG三个顶点的坐标分别为E(0,1),F(0,-1),G(2,1).当抛物线与
EFG的边有两个公共点时,直接写出m的取值范围.
18.如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(
,
)和B(4,m),直线AB交x轴于点E,点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
?
(1)求抛物线的解析式.
(2)连结AC、BC,是否存在一点P,使△ABC的面积等于14?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)若△PAC与△PDE相似,求点P的坐标.
19.如图,抛物线y=
x2+bx+c与x轴交于点A和点B
,
与y轴交于点C(0,﹣4),顶点为D
,
其对称轴直线x=1交x轴于点P
.
(1)求抛物线的解析式;
(2)如图1,线段MN的两端点M
,
N都在抛物线上(点M在对称轴左侧,点N在对称轴右侧),且MN=4,求四边形PMDN面积的最大值和此时点N的坐标;
(3)如图2,点Q是直线l:y=kx+1上一点,当以Q
,
A
,
C
,
B为顶点的四边形是平行四边形时,确定点Q的坐标和k的值.
20.如图,抛物线
与x轴交于A、B点(点B在点A的右侧),与y轴交于点C.连结BC,以BC为一边,点O为对称中心作菱形BCED,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A、B、C的坐标;
(2)当点P在线段OB上运动时,直线l分别交BD、BC于点M、N.试探究m为何值时,四边形CDMQ是平行四边形;
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
21.如图,抛物线
与
轴交于点
A,与x轴正半轴交于点
,点
C在线段
上,连接
,过点B作
交
y轴于点
E,点
在线段
上,且点M在点
之间,
.点
分别是线段
上的动点,当点
P从点A匀速运动到点
C时,点Q恰好从点M匀速运动到点N,设
,已知
.
(1)求抛物线的对称轴;
(2)求线段
和
的长;
(3)连接
,当直线
经过
的一个顶点时,请直接写出直线
与抛物线对称轴交点的纵坐标.
22.在平面直角坐标系中,点A在第一象限,
轴于点B
,
经过点B的函数图象的一部分(自变量大于0)记为
,将
沿y轴对折,再向下平移两个单位长度得到的图象记为
,图象
合起来得到的图象记为G
.
(1)若
,则OB的长度为:________;
(2)若
,其中m是常数,
①则图象
的函数关系式为:??▲??
;
②点
关于y轴对称且
,当
与线段
恰好有一个公共点时,求m的取值范围;
③设G在
上最高点的纵坐标为
,当
时,直接写出m的取值范围.
23.综合与实践
如图1,抛物线y=﹣
x2﹣
x+6与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C
.
(1)求直线AC的表达式;
(2)点E在抛物线的对称轴上,在平面内是否存在点F
,
使得以点A
,
C
,
E
,
F为顶点的四边形是矩形?若存在,请直接写出点E的坐标;若不存在,请说明理由;
(3)如图2,设点P从点O出发以1个单位长度/秒的速度向终点A运动,同时点Q从点A出发以
个单位长度/秒的速度向终点C运动,运动时间为t秒,当∠OPQ的平分线恰好经过OC的中点时,求t的值.
24.综合与探究.
如图,在平面直角坐标系中,抛物线y=﹣x2﹣3x+4与x轴分别交于点A和点B(点A在点B的左侧),交y轴于点C
.
点P是线段OA上的一个动点,沿OA以每秒1个单位长度的速度由点O向点A运动,过点P作DP⊥x轴,交抛物线于点D
,
交直线AC于点E
,
连接BE
.
(1)求直线AC的表达式;
(2)在点P运动过程中,运动时间为何值时,EC=ED?
(3)在点P运动过程中,△EBP的周长是否存在最小值?若存在,求出此时点P的坐标;若不存在,请说明理由.
25.如图,已知点
在抛物线
上.
(1)求抛物线的解析式;
(2)E在抛物线对称轴上,在平面内是否存在点F,使得以点B,C,E,F为顶点的四边形是矩形?若存在,请写出点F的坐标,若不存在,请说明理由;
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使
?若存在,求出Q点坐标;若不存在,说明理由.
26.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点
C.
(1)直接写出抛物线的解析式为:________;
(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G,H,设点D的横坐标为m.
①求DF+HF的最大值;
②连接EG,若∠GEH=45°,求m的值.
27.在平面直角坐标系
中,抛物线
经过点
,顶点为点B,对称轴为直线
,且对称轴与x轴交于点C.直线
,经过点A,与线段
交于点E.
(1)求抛物线
的表达式;
(2)联结
、
.当
的面积为3时,求直线
的表达式;
(3)在(2)的条件下,设点D为y轴上的一点,联结
、
,当
时,求
的余切值.
28.如图,在平面直角坐标系中,直线
交x轴,y轴于A,C两点,二次函数
的图象经过A,C两点,与x轴另一个交点是B.动点P从A点出发,沿
以每秒2个单位长度的速度,向终点B运动,过点P作
于点D.(点P不与点A,B重合)作
,边
交射线
于点Q.设P点运动时间为t.
(1)求二次函数关系式;
(2)设
与
重叠面积为S,求S与t之间函数关系;
(3)拋物线上是否存在点M,使
,若存在,直接写出点M坐标;若不存在,说明理由.
答案
一、选择题
1.
A
2.
C
3.
C
4.
A
5.
C
6.
D
7.
B
8.
C
二、填空题
9.
1010.
108
11.
;
12.
-15
13
当
时,
的长随
的增大而减小;当
时,
的长随
的增大而增大.
14.
③④
15.
16.
①④
三、解答题
17.
(1)解:
,
顶点坐标为(
,
).?
∵抛物线的顶点在第二象限
∴可得
,解得
.
(2)解:∵当-2≤x≤1时,y先随x的增大而增大,后随x的增大而减小,且抛物线对称轴x=m,
∴-2<m<1
当
时,
当
时,
∵当
时,y有最小值,
∴-m2+5m≤-m2-m-3,
解得
∴
.
∵m为整数,∴m=-1
(3)解:当m=1时,
,
设点A的坐标为(a,2),则点B的坐标为(a,
),
∴
或
.
∵
或
,
∴
或
.
解得
,
或
,
(不合题意,舍去).????????????
综上,点A的横坐标为
或
或
(4)
或
18.
(1)解:∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A(
,
),B(4,6)在抛物线y=ax2+bx+6上,
∴
,解得
,
∴抛物线的解析式为y=2x2﹣8x+6;
(2)解:设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),
∵点P是线段AB上异于A、B的动点,
∴
,
∴PC=(n+2)﹣(2n2﹣8n+6)=﹣2n2+9n﹣4,
假设△ABC的面积等于14,
则
PC?(xB﹣xA)=14,
∴
,
即:2n2﹣9n+12=0,
∵△=(-9)2﹣4×2×12<0,
∴一元二次方程无实数解,
∴假设不成立,
即:不存在一点P,使△ABC的面积等于14;
(3)解:∵PC⊥x轴,
∴∠PDE=90°,
∵△PAC与△PDE相似,
∴△PAC也是直角三角形,
①当P为直角顶点,则∠APC=90°
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
②若点A为直角顶点,则∠PAC=90°.
如图1,过点A(
,
)作AN⊥x轴于点N,则ON=
,AN=
.
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=
,
∴OM=ON+MN=
+
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则:
,解得
,
∴直线AM的解析式为:y=﹣x+3?
①
又抛物线的解析式为:y=2x2﹣8x+6
②
联立①②式,
解得:
或
(与点A重合,舍去),
∴C(3,0),即点C、M点重合.
当x=3时,y=x+2=5,
∴P1(3,5);
③若点C为直角顶点,则∠ACP=90°.
∵y=2x2﹣8x+6=2(x﹣2)2﹣2,
∴抛物线的对称轴为直线x=2.
如图2,作点A(
,
)关于对称轴x=2的对称点C,
则点C在抛物线上,且C(
,
).
当x=
时,y=x+2=
.
∴P2(
,
).
∵点P1(3,5)、P2(
,
)均在线段AB上,
∴综上所述,若△PAC与△PDE相似,点P的坐标为(3,5)或(
,
).
19.
(1)解:由题意得:
,解得
,
故抛物线的表达式为y=
x2﹣x﹣4;
(2)解:由抛物线解析式得点D坐标为(1,﹣
),
设四边形PMDN面积为S,
则S=S△PDM+S△PDN=
PD(xN﹣xM)=
(xN﹣xM),
故当MN与轴平行时,此时MN=4,S的面积最大,
则S=9,
此时点M、N关于抛物线对称轴对称,则点N的横坐标为3,
当x=3时,y=
x2﹣x﹣4=﹣2.5,
故点N的坐标为(3,﹣2.5);
(3)解:把y=0代入y=
x2﹣x﹣4得
x2﹣x﹣4=0,
解得:
,
∴点A(-2,0),点B(4,0)
设点Q的坐标为(m,km+1),
当AC为边时,如图1,
点A向右平移2个单位向下平移4个单位得到点C,同样点B向右平移2个单位向下平移4个单位得到点Q,
即
解得
,
故点Q的坐标和k分别为(6,﹣4)、﹣
;
如图2,
点A向右平移2个单位向下平移4个单位得到点C,同样点Q向右平移2个单位向下平移4个单位得到点B,
即
,解得
,
故点Q的坐标和k分别为(2,4)、1.5;
当AC是对角线时,
由中点公式得
解得
,
故点Q的坐标和k分别为(﹣6,﹣4)、﹣
;
综上,点Q的坐标和k分别为(6,﹣4)、﹣
或(2,4)、1.5或(﹣6,﹣4)、﹣
.
20.
(1)解:当y=0时,
,解得
∵点B在点A的右侧∴A(-2,0),B(8,0)
当x=0时,y=﹣4∴C(0,﹣4)
(2)解:由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则
解得
∴直线BD的解析式为
∵l⊥x轴,
当MQ=DC时,四边形CDMQ是平行四边形
化简得:m2-4m=0,解得m1=0(不合题意舍去),m2=4.
∴当m2=4时,四边形CDMQ是平行四边形.
(3)解:若△BDQ为直角三角形,可能有三种情形,如图所示:
由勾股定理得:AD=
∴△ABD为直角三角形
即点A为所求的点Q.
∴Q1(﹣2,0)
③以点B为直角顶点.
如图,设Q2点坐标为(x,y),过点Q2作Q2K⊥x轴于点K,则Q2K=﹣y
OK=x,BK=8﹣x.
易证△Q2KB∽△BOD,
即
整理得:y=2x﹣16
∵点Q在抛物线上,
解得x=6或x=8
当x=8时,点Q2与点B重合,故舍去;
当x=6时,y=﹣4.
∴Q2(6,﹣4)
综上所述,符合题意的点Q的坐标为(﹣2,0)或(6,﹣4).
21.
(1)解:将
,
代入
可得
,
抛物线的解析式为:
,
抛物线的对称轴为
.
(2)解:P在C点时,
,
,
令
,代入
,即
.
的坐标为
,
在
中,
,
,
由勾股定理可知
,
,
,
,
.
(3)
或
22.
(1)1
(2)解:①
;
②由①得:
的对称轴为
,A点在第一象限,
轴于点B,
∴
,
由点
关于y轴对称且
,知:点
的横坐标分别为4、-4,
∵
与线段
只有一个公共点,且
开口向下,则此点为
的顶点,
∵
的顶点坐标为(
,
),
∴
,
解得:
(负值舍去);
当
过点
时,有
,
解得:
,
而G2与线段
只有一个公共点时,
,
综上,
与线段
只有一个公共点时,
或
;
③
23.
(1)解:令
,得:
,
解得:
,
,
,
,
令
,得:
,
,
∴直线AC的表达式:
,
(2)解:对称轴:
,
设
,
,
,
由两点间距离公式得:
,
,
,
∵A、C、E、F为矩形,
∴A、C、E三点形成
,
①当
时,
∴
,
∴
,
解得:
,
,
②当
,
∴
,
∴
,
解得:
,
,
③当
,
∴
,
∴
,
解得:
,
,
,
,
综上所述:
、
、
、
,
(3)解:记OC中点D,作
于点H
,过点C作AO平行线交PQ于点G,连接DG,如图所示:
∵DP为角平分线
∴
,
∴
,
,
?
∴
,
∴
,
∴
,
?
?
∴
,
?
∴
,
?
∴
,
∴
,
∴
,
?
?
?直线AC的表达式:
,
?
,
设
的解析式为:
?
?
PQ的解析式为:
,
将点
代入PQ得,
,
解得:
,
,
经检验:
,
都是原方程的根,但
不合题意,舍去,
故
24.
(1)解:∵
抛物线y=﹣x2﹣3x+4与x轴分别交于A,B,交y轴于点C,
∴
当x=0时,y=4.
∴
C(0,4).
当y=0时,﹣x2﹣3x+4=0,
∴
x1=﹣4,x2=1,
∴
A(﹣4,0),B(1,0).
设直线AC的解析式为y=kx+b,
∴
解得:
∴
直线AC的表达式为y=x+4.
(2)解:设点P的运动时间为t秒,
∵点P以每秒1个单位长度的速度由点O向点A运动,
∴
OP=t.
∴
P(﹣t,0).
∵
A(﹣4,0),C(0,4),
∴
OA=OC=4.
∴
Rt△AOC为等腰直角三角形.
∴
∠CAO=∠ACO=45°,AC=
OA=4
.
∵
DP⊥x轴,
在Rt△APE中,∠CAP=45°,
∴
AP=PE=4﹣t,AE=
AP=
(4﹣t).
∴
EC=AC﹣AE=
t.
∵
E,P的横坐标相同,
∴
E(﹣t,﹣t+4),D(﹣t,﹣t2+3t+4).
∴
DE=(﹣t2+3t+4)﹣(﹣t+4)=﹣t2+4t.
∵
EC=DE,
∴﹣t2+4t=
t.
解得:t=0或t=4﹣
.
∴
当运动时间为0或(4﹣
)秒时,EC=ED.
(3)解:存在.P的坐标为(﹣
,0).
在Rt△AEP中,∠OAC=45°,
∴
AP=EP.
∴
△AEB的周长为EP+BP+BE=AP+BP+BE=AB+BE.
∵
AB=5,
∴
当BE最小时,△AEB的周长最小.
当BE⊥AC时,BE最小.
在Rt△AEB中,
∵∠AEB=90°,∠BAC=45°,AB=5,BE⊥AC,
∴
PB=
AB=
.
∴
OP=PB﹣OB=
.
∴
P(﹣
,0).
25.
(1)解:将点A、B、C的坐标代入抛物线表达式得
,解得
,
故抛物线的表达式为:
(2)解:由(1)
得,
抛物线的对称轴为:
;
设点E(1,y)、点F(s,t),
,
当BC为边时,点C向右平移3
个单位向下平移1个单位得到点B,
同样E(F)向右平移3
个单位向下平移1个单位得到点F(E),且BE=CF(CE=BF),
∴
或
,
解得:
,或
故点F的坐标为:(
,
)或(
,
);
当BC为对角线时,由中点公式和BC=EF得:
,
解得:
(舍去),或
,
故点F的坐标为(2,
)或(2,2);
综上所述,点F的坐标为(
,
)或(
,
)或(2,
)或(2,2)
(3)解:存在;
由点A、C的坐标知,∠CAB=45°=∠BQC,
∴点Q在△ABC的外接圆上,即A、Q、B、C四点共圆,
∵AB垂直于抛物线的对称轴,
∴该圆的圆心E在抛物线的对称轴上,
设点E的坐标为(1,m),
由CE=BC得:12+(m
1)2=(1
3)2+m2
,
解得m=
1,
故圆的半径为
,
则点Q的坐标为(1,
)
26.
(1)
(2)解:①当x=0时,
=3.
∴C(0,3),
又∵B(3,0),
所以直线BC的解析式为y=-x+3,
∵OB=OC=3,
∴∠OB
C=∠OC
B=45°
过点F作FK⊥y轴于点K,如下图
又∵FH⊥BC,
∴∠
KFH=∠K
HF=45°,
∴.FH=
KF=
OE
∴DF+HF=DE-EF+
OE
=
(-m2+2m+3)
-
(-m+3)
+
m
=-m2+
(3+
)
m,
由题意得,0又-1<0
∴当m=
时,DF+HF取得最大值,
DF+HF的最大值为:
;
②过点G作GM⊥y轴于点M,记直线FH与x轴交于点N,
∵FK⊥y轴,DE⊥x轴,∠
KFH=45°,
∴∠EFH=∠ENF=45°,
∴EF=EN,
∵
∠KHF=
∠ONH=45°,
∴OH=ON,
∵
的对称轴为直线x=1,
∴
MG=1,
∴HG=
MG=
,
∵
∠GEH=45°,
∴∠GEH=∠EFH,
∵
∠EHF=∠GHE,
∴△EHG~△FHE,
∴
∴
?
在Rt△OEH中,
OH=ON=|OE-EN|
=|OE-EF|=|m-
(-m+3)
|=|2m-3|
又OE=m,
∴HE2=OE2+OH2,即
2m=m2+
(2m-3)
2,
解得:m=1或
27.
(1)解:∵抛物线
经过点
,对称轴为直线
,
∴
,
∴
∴抛物线表达式为
;
(2)解:把
代入
得y=4,
∴抛物线顶点B坐标为
,
由
的面积为3得
,
∴BE=2,
∵点E在线段BC上,
∴点E坐标为
,
把点
和点
代入
得
,
∴
,
∴直线表达式为
;
(3)解:如图,①若
,如图
,
则四边形
为平行四边形:
则点
坐标为
,
连接
,
∴
;
②若
与
不平行,如图
,
则四边形
为等腰梯形:
作BF⊥y轴于F,则
,
∴点
坐标为
,
连接
,
∴
,
综上所述,此时
的余切值为
或
.
28.
(1)解:∵直线
与x轴,y轴交于点A,C
∴
,
∵二次函数
经过A,C两点
∴
解得
∴二次函数关系式为:
(2)解:在
中,
∴
∵
∴
∴
当点Q和点C重合时,
,
当
时
在
中,
,
∴
,
当
时,
在
中,
,
?∴CE=CQ
tan∠CQE,
∴
2
(t-1)
∴
∴
(3)解:
,
∵∠OAC=30°,即∠BAC=30°,
若M在第二象限,设M
,作MN⊥x轴于点N,如图,
∴MN=-
,ON=-x,
∴BN=ON+OB=1-x,
在Rt△MNB中,tan∠ABM=
,
即:
解得:x=-2或x=1(舍去)
当x=-2时,-
=-
,
∴M点的坐标为(-2,
);
若M在第三象限,设M
,作M’N’⊥x轴于点N’,
此时,M?N?=-(-
)=
,
ON?=-x,BN?=1-x,
∴tan∠ABM?=
,即
,
解得:
(舍去),
当x=-4时,
-
=-
=-
;
此时,M?(-4,
)
故M(-2,
)或(-4,
).
一、选择题
1.二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①abc>0;②4a+2b+c>0;③5a﹣b+c=0;④若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2
,
且x1<x2
,
则﹣5<x1<x2<1;⑤若方程|ax2+bx+c|=2有四个根,则这四个根的和为﹣4.其中正确的结论有(??
)
A.?2个??????????????????????B.?3个??????????????????C.?4个????????????????????????D.?5个
2.如图,二次函数
的图象如图所示,下列结论:①
;②
;③一元二次方程
有两个不相等的实数根;④当
或
时,
.上述结论中正确的个数是(???
)
A.?1个????????????????????B.?2个????????????????C.?3个????????????????????????????D.?4个
3.抛物线
(a
,
b
,
c为常数,且
)经过点
和
,且
,当
时,y随着x的增大而减小,有下列结论:①
;②若点
,点
都在抛物线上,则
;③
.其中,正确结论的个数为(???
)
A.?0??????????????????B.?1?????????????????????????C.?2??????????????????????????D.?3
4.已知当
时,二次函数
的值恒大于1,则k的取值范围是(??
)
A.?k≥
??????????B.?-
≤k≤-
????????C.?-
<k<0?????????D.?-
≤k<0
5.如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是(??
)
A.?不变??????B.?一直变大?????????C.?先减小后增大????????????D.?先增大后减小
6.二次函数
,当
且
时,y的最小值为
,最大值为
,则
的值为(????
)
A.????????????????????B.???????????????????C.????????????????????D.?
7.已知抛物线y=ax2+bx+c(a<0)的对称轴为x=-1,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有(??
)
A.?2个?????????????B.?3个???????????????C.?4个????????????????D.?5个
8.已知二次函数y=a(x-2)2+c,当x=
x1时,函数值为y1;当x=
x2时,函数值为y2.若|x1-2|>|x2-2|,下列表达式中正确的是(????
)
A.?y1+y2>0??????B.?y1-y2>0?????????C.?a(y1-y2)>0???????D.?a(y1+y2)>0
二、填空题
9.在平面直角坐标系xOy中,抛物线y=-x2+6x-8与x轴交于点A
,
B(点A在点B的左侧),与y轴交于点C
.
垂直于y轴的直线l与抛物线交于点P(x1
,
y1),Q(x2
,
y2),与直线BC交于点N(x3
,
y3),若x1
记s=x1+x2+x3
,
则s的取值范围为________.
10.如图,一段抛物线:
,记为
,它与x轴交于两点O,
;将
绕
旋转
得到
,交x轴于
;将
绕
旋转
得到
,交x轴于
,过抛物线
,
顶点的直线与
、
、
围成的如图中的阴影部分,那么该阴影部分的面积为________.
11.“水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图
1
所示,碗体
DEC
呈抛物线状(碗体厚度不计),点
E
是抛物线的顶点,碗底高
EF=1cm,碗底宽
AB=2
cm,当瓷碗中装满面汤时,液面宽
CD=83cm,此时面汤最大深度
EG=6cm,将瓷碗绕点
B
缓缓倾斜倒出部分面汤,如图2,当
LABK=30
时停止,此时液面
CH
到桌面的距离为________cm;碗内面汤的最大深度是________cm.
12.如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则﹣1﹣b+c的最小值是________.
13.已知抛物线
的顶点为
,对称轴
与
轴交于点
,
是
的中点.
在抛物线上,
关于直线
的对称点为
,
关于点
的对称点为
.当
时,线段
的长随
的增大而发生的变化是:________.(“变化”是指增减情况及相应
的取值范围)
14.如图,已知二次函数
的图象与
轴交于不同两点,与
轴的交点在
轴正半轴,它的对称轴为直线
.有以下结论:①
,②
,③若点
和
在该图象上,则
,④设
,
是方程
的两根,若
,则
.其中正确的结论是________(填入正确结论的序号).
15.已知函数
的图象与函数
的图象恰好有四个交点,则
的取值范围是________.
16.如图,抛物线
与
交于点
,过点
作
轴的平行线,分别交两条抛物线于点
,
.则以下结论:①无论
取何值,
2的值总是正数;②
;③当
时,
;④
.其中正确结论是________.
三、解答题
17.在平面直角坐标系中,已知抛物线
(m为常数).
(1)当抛物线的顶点在第二象限时,求m的取值范围.
(2)当-2≤x≤1时,y先随x的增大而增大,后随x的增大而减小,且当x=1时y有最小值,求整数m的值
(3)当m=1时,点A是直线y=2上一点,过点A作y轴的平行线交抛物线于点B
,
以线段AB为边作正方形ABCD
,
使CD与y轴在的AB的同侧.若点C落在抛物线上,求点A的横坐标.
(4)已知
EFG三个顶点的坐标分别为E(0,1),F(0,-1),G(2,1).当抛物线与
EFG的边有两个公共点时,直接写出m的取值范围.
18.如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(
,
)和B(4,m),直线AB交x轴于点E,点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
?
(1)求抛物线的解析式.
(2)连结AC、BC,是否存在一点P,使△ABC的面积等于14?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)若△PAC与△PDE相似,求点P的坐标.
19.如图,抛物线y=
x2+bx+c与x轴交于点A和点B
,
与y轴交于点C(0,﹣4),顶点为D
,
其对称轴直线x=1交x轴于点P
.
(1)求抛物线的解析式;
(2)如图1,线段MN的两端点M
,
N都在抛物线上(点M在对称轴左侧,点N在对称轴右侧),且MN=4,求四边形PMDN面积的最大值和此时点N的坐标;
(3)如图2,点Q是直线l:y=kx+1上一点,当以Q
,
A
,
C
,
B为顶点的四边形是平行四边形时,确定点Q的坐标和k的值.
20.如图,抛物线
与x轴交于A、B点(点B在点A的右侧),与y轴交于点C.连结BC,以BC为一边,点O为对称中心作菱形BCED,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A、B、C的坐标;
(2)当点P在线段OB上运动时,直线l分别交BD、BC于点M、N.试探究m为何值时,四边形CDMQ是平行四边形;
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
21.如图,抛物线
与
轴交于点
A,与x轴正半轴交于点
,点
C在线段
上,连接
,过点B作
交
y轴于点
E,点
在线段
上,且点M在点
之间,
.点
分别是线段
上的动点,当点
P从点A匀速运动到点
C时,点Q恰好从点M匀速运动到点N,设
,已知
.
(1)求抛物线的对称轴;
(2)求线段
和
的长;
(3)连接
,当直线
经过
的一个顶点时,请直接写出直线
与抛物线对称轴交点的纵坐标.
22.在平面直角坐标系中,点A在第一象限,
轴于点B
,
经过点B的函数图象的一部分(自变量大于0)记为
,将
沿y轴对折,再向下平移两个单位长度得到的图象记为
,图象
合起来得到的图象记为G
.
(1)若
,则OB的长度为:________;
(2)若
,其中m是常数,
①则图象
的函数关系式为:??▲??
;
②点
关于y轴对称且
,当
与线段
恰好有一个公共点时,求m的取值范围;
③设G在
上最高点的纵坐标为
,当
时,直接写出m的取值范围.
23.综合与实践
如图1,抛物线y=﹣
x2﹣
x+6与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C
.
(1)求直线AC的表达式;
(2)点E在抛物线的对称轴上,在平面内是否存在点F
,
使得以点A
,
C
,
E
,
F为顶点的四边形是矩形?若存在,请直接写出点E的坐标;若不存在,请说明理由;
(3)如图2,设点P从点O出发以1个单位长度/秒的速度向终点A运动,同时点Q从点A出发以
个单位长度/秒的速度向终点C运动,运动时间为t秒,当∠OPQ的平分线恰好经过OC的中点时,求t的值.
24.综合与探究.
如图,在平面直角坐标系中,抛物线y=﹣x2﹣3x+4与x轴分别交于点A和点B(点A在点B的左侧),交y轴于点C
.
点P是线段OA上的一个动点,沿OA以每秒1个单位长度的速度由点O向点A运动,过点P作DP⊥x轴,交抛物线于点D
,
交直线AC于点E
,
连接BE
.
(1)求直线AC的表达式;
(2)在点P运动过程中,运动时间为何值时,EC=ED?
(3)在点P运动过程中,△EBP的周长是否存在最小值?若存在,求出此时点P的坐标;若不存在,请说明理由.
25.如图,已知点
在抛物线
上.
(1)求抛物线的解析式;
(2)E在抛物线对称轴上,在平面内是否存在点F,使得以点B,C,E,F为顶点的四边形是矩形?若存在,请写出点F的坐标,若不存在,请说明理由;
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使
?若存在,求出Q点坐标;若不存在,说明理由.
26.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点
C.
(1)直接写出抛物线的解析式为:________;
(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G,H,设点D的横坐标为m.
①求DF+HF的最大值;
②连接EG,若∠GEH=45°,求m的值.
27.在平面直角坐标系
中,抛物线
经过点
,顶点为点B,对称轴为直线
,且对称轴与x轴交于点C.直线
,经过点A,与线段
交于点E.
(1)求抛物线
的表达式;
(2)联结
、
.当
的面积为3时,求直线
的表达式;
(3)在(2)的条件下,设点D为y轴上的一点,联结
、
,当
时,求
的余切值.
28.如图,在平面直角坐标系中,直线
交x轴,y轴于A,C两点,二次函数
的图象经过A,C两点,与x轴另一个交点是B.动点P从A点出发,沿
以每秒2个单位长度的速度,向终点B运动,过点P作
于点D.(点P不与点A,B重合)作
,边
交射线
于点Q.设P点运动时间为t.
(1)求二次函数关系式;
(2)设
与
重叠面积为S,求S与t之间函数关系;
(3)拋物线上是否存在点M,使
,若存在,直接写出点M坐标;若不存在,说明理由.
答案
一、选择题
1.
A
2.
C
3.
C
4.
A
5.
C
6.
D
7.
B
8.
C
二、填空题
9.
10
108
11.
;
12.
-15
13
当
时,
的长随
的增大而减小;当
时,
的长随
的增大而增大.
14.
③④
15.
16.
①④
三、解答题
17.
(1)解:
,
顶点坐标为(
,
).?
∵抛物线的顶点在第二象限
∴可得
,解得
.
(2)解:∵当-2≤x≤1时,y先随x的增大而增大,后随x的增大而减小,且抛物线对称轴x=m,
∴-2<m<1
当
时,
当
时,
∵当
时,y有最小值,
∴-m2+5m≤-m2-m-3,
解得
∴
.
∵m为整数,∴m=-1
(3)解:当m=1时,
,
设点A的坐标为(a,2),则点B的坐标为(a,
),
∴
或
.
∵
或
,
∴
或
.
解得
,
或
,
(不合题意,舍去).????????????
综上,点A的横坐标为
或
或
(4)
或
18.
(1)解:∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A(
,
),B(4,6)在抛物线y=ax2+bx+6上,
∴
,解得
,
∴抛物线的解析式为y=2x2﹣8x+6;
(2)解:设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),
∵点P是线段AB上异于A、B的动点,
∴
,
∴PC=(n+2)﹣(2n2﹣8n+6)=﹣2n2+9n﹣4,
假设△ABC的面积等于14,
则
PC?(xB﹣xA)=14,
∴
,
即:2n2﹣9n+12=0,
∵△=(-9)2﹣4×2×12<0,
∴一元二次方程无实数解,
∴假设不成立,
即:不存在一点P,使△ABC的面积等于14;
(3)解:∵PC⊥x轴,
∴∠PDE=90°,
∵△PAC与△PDE相似,
∴△PAC也是直角三角形,
①当P为直角顶点,则∠APC=90°
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
②若点A为直角顶点,则∠PAC=90°.
如图1,过点A(
,
)作AN⊥x轴于点N,则ON=
,AN=
.
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=
,
∴OM=ON+MN=
+
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则:
,解得
,
∴直线AM的解析式为:y=﹣x+3?
①
又抛物线的解析式为:y=2x2﹣8x+6
②
联立①②式,
解得:
或
(与点A重合,舍去),
∴C(3,0),即点C、M点重合.
当x=3时,y=x+2=5,
∴P1(3,5);
③若点C为直角顶点,则∠ACP=90°.
∵y=2x2﹣8x+6=2(x﹣2)2﹣2,
∴抛物线的对称轴为直线x=2.
如图2,作点A(
,
)关于对称轴x=2的对称点C,
则点C在抛物线上,且C(
,
).
当x=
时,y=x+2=
.
∴P2(
,
).
∵点P1(3,5)、P2(
,
)均在线段AB上,
∴综上所述,若△PAC与△PDE相似,点P的坐标为(3,5)或(
,
).
19.
(1)解:由题意得:
,解得
,
故抛物线的表达式为y=
x2﹣x﹣4;
(2)解:由抛物线解析式得点D坐标为(1,﹣
),
设四边形PMDN面积为S,
则S=S△PDM+S△PDN=
PD(xN﹣xM)=
(xN﹣xM),
故当MN与轴平行时,此时MN=4,S的面积最大,
则S=9,
此时点M、N关于抛物线对称轴对称,则点N的横坐标为3,
当x=3时,y=
x2﹣x﹣4=﹣2.5,
故点N的坐标为(3,﹣2.5);
(3)解:把y=0代入y=
x2﹣x﹣4得
x2﹣x﹣4=0,
解得:
,
∴点A(-2,0),点B(4,0)
设点Q的坐标为(m,km+1),
当AC为边时,如图1,
点A向右平移2个单位向下平移4个单位得到点C,同样点B向右平移2个单位向下平移4个单位得到点Q,
即
解得
,
故点Q的坐标和k分别为(6,﹣4)、﹣
;
如图2,
点A向右平移2个单位向下平移4个单位得到点C,同样点Q向右平移2个单位向下平移4个单位得到点B,
即
,解得
,
故点Q的坐标和k分别为(2,4)、1.5;
当AC是对角线时,
由中点公式得
解得
,
故点Q的坐标和k分别为(﹣6,﹣4)、﹣
;
综上,点Q的坐标和k分别为(6,﹣4)、﹣
或(2,4)、1.5或(﹣6,﹣4)、﹣
.
20.
(1)解:当y=0时,
,解得
∵点B在点A的右侧∴A(-2,0),B(8,0)
当x=0时,y=﹣4∴C(0,﹣4)
(2)解:由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则
解得
∴直线BD的解析式为
∵l⊥x轴,
当MQ=DC时,四边形CDMQ是平行四边形
化简得:m2-4m=0,解得m1=0(不合题意舍去),m2=4.
∴当m2=4时,四边形CDMQ是平行四边形.
(3)解:若△BDQ为直角三角形,可能有三种情形,如图所示:
由勾股定理得:AD=
∴△ABD为直角三角形
即点A为所求的点Q.
∴Q1(﹣2,0)
③以点B为直角顶点.
如图,设Q2点坐标为(x,y),过点Q2作Q2K⊥x轴于点K,则Q2K=﹣y
OK=x,BK=8﹣x.
易证△Q2KB∽△BOD,
即
整理得:y=2x﹣16
∵点Q在抛物线上,
解得x=6或x=8
当x=8时,点Q2与点B重合,故舍去;
当x=6时,y=﹣4.
∴Q2(6,﹣4)
综上所述,符合题意的点Q的坐标为(﹣2,0)或(6,﹣4).
21.
(1)解:将
,
代入
可得
,
抛物线的解析式为:
,
抛物线的对称轴为
.
(2)解:P在C点时,
,
,
令
,代入
,即
.
的坐标为
,
在
中,
,
,
由勾股定理可知
,
,
,
,
.
(3)
或
22.
(1)1
(2)解:①
;
②由①得:
的对称轴为
,A点在第一象限,
轴于点B,
∴
,
由点
关于y轴对称且
,知:点
的横坐标分别为4、-4,
∵
与线段
只有一个公共点,且
开口向下,则此点为
的顶点,
∵
的顶点坐标为(
,
),
∴
,
解得:
(负值舍去);
当
过点
时,有
,
解得:
,
而G2与线段
只有一个公共点时,
,
综上,
与线段
只有一个公共点时,
或
;
③
23.
(1)解:令
,得:
,
解得:
,
,
,
,
令
,得:
,
,
∴直线AC的表达式:
,
(2)解:对称轴:
,
设
,
,
,
由两点间距离公式得:
,
,
,
∵A、C、E、F为矩形,
∴A、C、E三点形成
,
①当
时,
∴
,
∴
,
解得:
,
,
②当
,
∴
,
∴
,
解得:
,
,
③当
,
∴
,
∴
,
解得:
,
,
,
,
综上所述:
、
、
、
,
(3)解:记OC中点D,作
于点H
,过点C作AO平行线交PQ于点G,连接DG,如图所示:
∵DP为角平分线
∴
,
∴
,
,
?
∴
,
∴
,
∴
,
?
?
∴
,
?
∴
,
?
∴
,
∴
,
∴
,
?
?
?直线AC的表达式:
,
?
,
设
的解析式为:
?
?
PQ的解析式为:
,
将点
代入PQ得,
,
解得:
,
,
经检验:
,
都是原方程的根,但
不合题意,舍去,
故
24.
(1)解:∵
抛物线y=﹣x2﹣3x+4与x轴分别交于A,B,交y轴于点C,
∴
当x=0时,y=4.
∴
C(0,4).
当y=0时,﹣x2﹣3x+4=0,
∴
x1=﹣4,x2=1,
∴
A(﹣4,0),B(1,0).
设直线AC的解析式为y=kx+b,
∴
解得:
∴
直线AC的表达式为y=x+4.
(2)解:设点P的运动时间为t秒,
∵点P以每秒1个单位长度的速度由点O向点A运动,
∴
OP=t.
∴
P(﹣t,0).
∵
A(﹣4,0),C(0,4),
∴
OA=OC=4.
∴
Rt△AOC为等腰直角三角形.
∴
∠CAO=∠ACO=45°,AC=
OA=4
.
∵
DP⊥x轴,
在Rt△APE中,∠CAP=45°,
∴
AP=PE=4﹣t,AE=
AP=
(4﹣t).
∴
EC=AC﹣AE=
t.
∵
E,P的横坐标相同,
∴
E(﹣t,﹣t+4),D(﹣t,﹣t2+3t+4).
∴
DE=(﹣t2+3t+4)﹣(﹣t+4)=﹣t2+4t.
∵
EC=DE,
∴﹣t2+4t=
t.
解得:t=0或t=4﹣
.
∴
当运动时间为0或(4﹣
)秒时,EC=ED.
(3)解:存在.P的坐标为(﹣
,0).
在Rt△AEP中,∠OAC=45°,
∴
AP=EP.
∴
△AEB的周长为EP+BP+BE=AP+BP+BE=AB+BE.
∵
AB=5,
∴
当BE最小时,△AEB的周长最小.
当BE⊥AC时,BE最小.
在Rt△AEB中,
∵∠AEB=90°,∠BAC=45°,AB=5,BE⊥AC,
∴
PB=
AB=
.
∴
OP=PB﹣OB=
.
∴
P(﹣
,0).
25.
(1)解:将点A、B、C的坐标代入抛物线表达式得
,解得
,
故抛物线的表达式为:
(2)解:由(1)
得,
抛物线的对称轴为:
;
设点E(1,y)、点F(s,t),
,
当BC为边时,点C向右平移3
个单位向下平移1个单位得到点B,
同样E(F)向右平移3
个单位向下平移1个单位得到点F(E),且BE=CF(CE=BF),
∴
或
,
解得:
,或
故点F的坐标为:(
,
)或(
,
);
当BC为对角线时,由中点公式和BC=EF得:
,
解得:
(舍去),或
,
故点F的坐标为(2,
)或(2,2);
综上所述,点F的坐标为(
,
)或(
,
)或(2,
)或(2,2)
(3)解:存在;
由点A、C的坐标知,∠CAB=45°=∠BQC,
∴点Q在△ABC的外接圆上,即A、Q、B、C四点共圆,
∵AB垂直于抛物线的对称轴,
∴该圆的圆心E在抛物线的对称轴上,
设点E的坐标为(1,m),
由CE=BC得:12+(m
1)2=(1
3)2+m2
,
解得m=
1,
故圆的半径为
,
则点Q的坐标为(1,
)
26.
(1)
(2)解:①当x=0时,
=3.
∴C(0,3),
又∵B(3,0),
所以直线BC的解析式为y=-x+3,
∵OB=OC=3,
∴∠OB
C=∠OC
B=45°
过点F作FK⊥y轴于点K,如下图
又∵FH⊥BC,
∴∠
KFH=∠K
HF=45°,
∴.FH=
KF=
OE
∴DF+HF=DE-EF+
OE
=
(-m2+2m+3)
-
(-m+3)
+
m
=-m2+
(3+
)
m,
由题意得,0
∴当m=
时,DF+HF取得最大值,
DF+HF的最大值为:
;
②过点G作GM⊥y轴于点M,记直线FH与x轴交于点N,
∵FK⊥y轴,DE⊥x轴,∠
KFH=45°,
∴∠EFH=∠ENF=45°,
∴EF=EN,
∵
∠KHF=
∠ONH=45°,
∴OH=ON,
∵
的对称轴为直线x=1,
∴
MG=1,
∴HG=
MG=
,
∵
∠GEH=45°,
∴∠GEH=∠EFH,
∵
∠EHF=∠GHE,
∴△EHG~△FHE,
∴
∴
?
在Rt△OEH中,
OH=ON=|OE-EN|
=|OE-EF|=|m-
(-m+3)
|=|2m-3|
又OE=m,
∴HE2=OE2+OH2,即
2m=m2+
(2m-3)
2,
解得:m=1或
27.
(1)解:∵抛物线
经过点
,对称轴为直线
,
∴
,
∴
∴抛物线表达式为
;
(2)解:把
代入
得y=4,
∴抛物线顶点B坐标为
,
由
的面积为3得
,
∴BE=2,
∵点E在线段BC上,
∴点E坐标为
,
把点
和点
代入
得
,
∴
,
∴直线表达式为
;
(3)解:如图,①若
,如图
,
则四边形
为平行四边形:
则点
坐标为
,
连接
,
∴
;
②若
与
不平行,如图
,
则四边形
为等腰梯形:
作BF⊥y轴于F,则
,
∴点
坐标为
,
连接
,
∴
,
综上所述,此时
的余切值为
或
.
28.
(1)解:∵直线
与x轴,y轴交于点A,C
∴
,
∵二次函数
经过A,C两点
∴
解得
∴二次函数关系式为:
(2)解:在
中,
∴
∵
∴
∴
当点Q和点C重合时,
,
当
时
在
中,
,
∴
,
当
时,
在
中,
,
?∴CE=CQ
tan∠CQE,
∴
2
(t-1)
∴
∴
(3)解:
,
∵∠OAC=30°,即∠BAC=30°,
若M在第二象限,设M
,作MN⊥x轴于点N,如图,
∴MN=-
,ON=-x,
∴BN=ON+OB=1-x,
在Rt△MNB中,tan∠ABM=
,
即:
解得:x=-2或x=1(舍去)
当x=-2时,-
=-
,
∴M点的坐标为(-2,
);
若M在第三象限,设M
,作M’N’⊥x轴于点N’,
此时,M?N?=-(-
)=
,
ON?=-x,BN?=1-x,
∴tan∠ABM?=
,即
,
解得:
(舍去),
当x=-4时,
-
=-
=-
;
此时,M?(-4,
)
故M(-2,
)或(-4,
).
同课章节目录
