人教版A高一数学必修1 第一章第三节函数的基本性质1.3.1单调性与最大(小)值(共36张PPT)
文档属性
| 名称 | 人教版A高一数学必修1 第一章第三节函数的基本性质1.3.1单调性与最大(小)值(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 516.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 13:40:34 | ||
图片预览











文档简介
(共36张PPT)
1.3.1单调性与最大(小)值
[最新考纲]
1.理解函数的单调性、最大值、最小值及其几何意义.
2.会运用函数图象理解和研究函数的单调性.
知
识
梳
理
1.函数的单调性
(1)单调函数的定义
增函数
减函数
定义
一般地,设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量x1,x2
当x1<x2时,都有
,那么就说函数f(x)在区间D上是增函数
当x1<x2时,都有
,那么就说函数f(x)在区间D上是减函数
f(x1)<
f(x2)
f(x1)>
f(x2)
续表
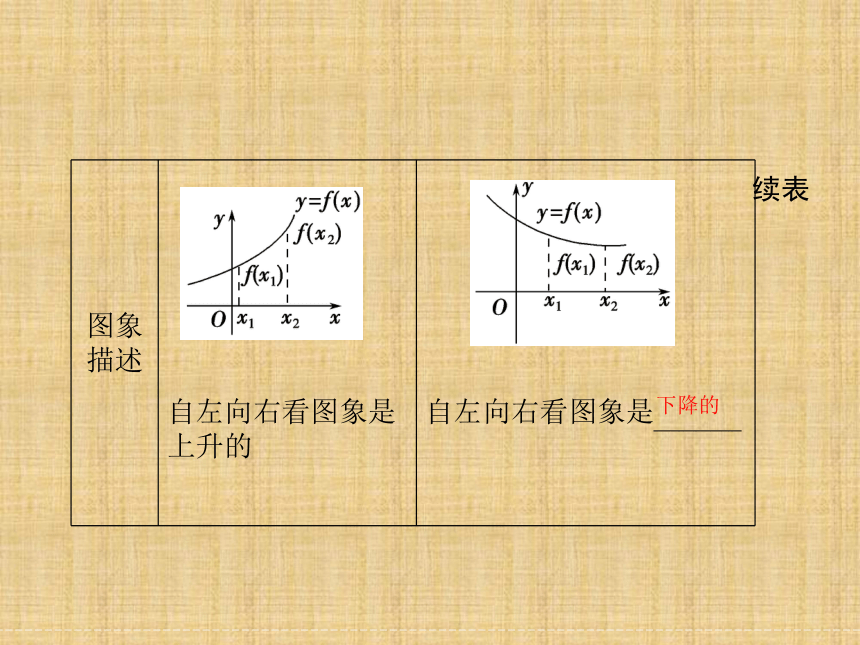
图象
描述
自左向右看图象是上升的
自左向右看图象是
下降的
(2)单调区间的定义
若函数y=f(x)在区间D上是
或
,则称函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做函数y=f(x)的单调区间.
增函数
减函数
2.函数的最值
前提
设函数y=f(x)的定义域为I,如果存在实数M满足
条件
(1)对于任意x∈I,都有
;
(2)存在x0∈I,使得f(x0)=M.
(3)对于任意x∈I,都有
;
(4)存在x0∈I,使得
.
结论
M为最大值
M为最小值
f(x)≤M
f(x)≥M
f(x0)=M
辨
析
感
悟
1.函数单调性定义的理解
(1)对于函数f(x),x∈D,若x1,x2∈D且(x1-x2)[f(x1)-f(x2)]>0,则函数f(x)在D上是增函数.
(√)
(2)函数f(x)=2x+1在(-∞,+∞)上是增函数.
(√)
[感悟·提升]
1.一个区别 “函数的单调区间”和“函数在某区间上单调”的区别:前者指函数具备单调性的“最大”的区间,后者是前者“最大”区间的子集,如(5).
2.两个防范 一是注意函数的定义域不连续的两个单调性相同的区间,要分别说明单调区间,不可说成“在其定义域上”单调,如(3);
二是若函数在两个不同的区间上单调性相同,则这两个区间要分开写,不能写成并集,如(6).
考点一 确定函数的单调性或单调区间
规律方法
(1)对于给出具体解析式的函数,证明或判断其在某区间上的单调性有两种方法:①可以利用定义(基本步骤为取值、作差或作商、变形、定号、下结论)求解;②可导函数则可以利用导数解之.
(2)复合函数y=f[g(x)]的单调性规律是“同则增,异则减”,即y=f(u)与u=g(x)若具有相同的单调性,则y=f[g(x)]为增函数,若具有不同的单调性,则y=f[g(x)]必为减函数.
考点二 利用单调性求参数
规律方法
利用单调性求参数的一般方法:一是求出函数的单调区间,然后使所给区间是这个单调区间的子区间,建立关于参数的不等式组即可求得参数范围;二是直接利用函数单调性的定义:作差、变形,由f(x1)-f(x2)的符号确定参数的范围,另外也可分离参数转化为不等式恒成立问题.
(2)f(x)在[a,+∞)上是减函数,对于g(x),只有当a>0时,它有两个减区间为(-∞,-1)和(-1,+∞),故只需区间[1,2]是f(x)和g(x)的减区间的子集即可,则a的取值范围是0答案 (1)C (2)D
考点三 利用函数的单调性求最值
规律方法
求函数最值的常用方法:
(1)单调性法:先确定函数的单调性,再由单调性求最值;
(2)图象法:先作出函数的图象,再观察其最高点、最低点,求出最值;
(3)基本不等式法:先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求出最值;
(4)导数法:先求导,然后求出在给定区间上的极值,最后结合端点值,求出最值;
(5)换元法:对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求最值.
答案 -1
1.求函数的单调区间:首先应注意函数的单调区间是其定义域的子集;其次掌握一次函数、二次函数等基本初等函数的单调区间.求函数单调区间的常用方法:根据定义、利用图象、单调函数的性质及利用导数的性质.
2.复合函数的单调性:对于复合函数y=f[g(x)],若t=g(x)在区间(a,b)上是单调函数,且y=f(t)在区间(g(a),g(b))或者(g(b),g(a))上是单调函数,若t=g(x)与y=f(t)的单调性相同(同时为增或减),则y=f[g(x)]为增函数;若t=g(x)与y=f(t)的单调性相反,则y=f[g(x)]为减函数.简称:同增异减.
3.函数的值域常常化归为求函数的最值问题,要重视函数的单调性在确定函数最值过程中的应用.
易错辨析1——分段函数单调性的判定
[防范措施] 对于分段函数的单调性,有两种基本的判断方法:一保证各段上同增(减)时,要注意上、下段间端点值间的大小关系;二是画出这个分段函数的图象,结合函数图象、性质进行直观的判断.研究函数问题离不开函数图象,函数图象反映了函数的所有性质,在研究函数问题时要时时刻刻想到函数的图象,学会从函数图象上去分析问题、寻找解决问题的方法.
答案 C
1.3.1单调性与最大(小)值
[最新考纲]
1.理解函数的单调性、最大值、最小值及其几何意义.
2.会运用函数图象理解和研究函数的单调性.
知
识
梳
理
1.函数的单调性
(1)单调函数的定义
增函数
减函数
定义
一般地,设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量x1,x2
当x1<x2时,都有
,那么就说函数f(x)在区间D上是增函数
当x1<x2时,都有
,那么就说函数f(x)在区间D上是减函数
f(x1)<
f(x2)
f(x1)>
f(x2)
续表
图象
描述
自左向右看图象是上升的
自左向右看图象是
下降的
(2)单调区间的定义
若函数y=f(x)在区间D上是
或
,则称函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做函数y=f(x)的单调区间.
增函数
减函数
2.函数的最值
前提
设函数y=f(x)的定义域为I,如果存在实数M满足
条件
(1)对于任意x∈I,都有
;
(2)存在x0∈I,使得f(x0)=M.
(3)对于任意x∈I,都有
;
(4)存在x0∈I,使得
.
结论
M为最大值
M为最小值
f(x)≤M
f(x)≥M
f(x0)=M
辨
析
感
悟
1.函数单调性定义的理解
(1)对于函数f(x),x∈D,若x1,x2∈D且(x1-x2)[f(x1)-f(x2)]>0,则函数f(x)在D上是增函数.
(√)
(2)函数f(x)=2x+1在(-∞,+∞)上是增函数.
(√)
[感悟·提升]
1.一个区别 “函数的单调区间”和“函数在某区间上单调”的区别:前者指函数具备单调性的“最大”的区间,后者是前者“最大”区间的子集,如(5).
2.两个防范 一是注意函数的定义域不连续的两个单调性相同的区间,要分别说明单调区间,不可说成“在其定义域上”单调,如(3);
二是若函数在两个不同的区间上单调性相同,则这两个区间要分开写,不能写成并集,如(6).
考点一 确定函数的单调性或单调区间
规律方法
(1)对于给出具体解析式的函数,证明或判断其在某区间上的单调性有两种方法:①可以利用定义(基本步骤为取值、作差或作商、变形、定号、下结论)求解;②可导函数则可以利用导数解之.
(2)复合函数y=f[g(x)]的单调性规律是“同则增,异则减”,即y=f(u)与u=g(x)若具有相同的单调性,则y=f[g(x)]为增函数,若具有不同的单调性,则y=f[g(x)]必为减函数.
考点二 利用单调性求参数
规律方法
利用单调性求参数的一般方法:一是求出函数的单调区间,然后使所给区间是这个单调区间的子区间,建立关于参数的不等式组即可求得参数范围;二是直接利用函数单调性的定义:作差、变形,由f(x1)-f(x2)的符号确定参数的范围,另外也可分离参数转化为不等式恒成立问题.
(2)f(x)在[a,+∞)上是减函数,对于g(x),只有当a>0时,它有两个减区间为(-∞,-1)和(-1,+∞),故只需区间[1,2]是f(x)和g(x)的减区间的子集即可,则a的取值范围是0
考点三 利用函数的单调性求最值
规律方法
求函数最值的常用方法:
(1)单调性法:先确定函数的单调性,再由单调性求最值;
(2)图象法:先作出函数的图象,再观察其最高点、最低点,求出最值;
(3)基本不等式法:先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求出最值;
(4)导数法:先求导,然后求出在给定区间上的极值,最后结合端点值,求出最值;
(5)换元法:对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求最值.
答案 -1
1.求函数的单调区间:首先应注意函数的单调区间是其定义域的子集;其次掌握一次函数、二次函数等基本初等函数的单调区间.求函数单调区间的常用方法:根据定义、利用图象、单调函数的性质及利用导数的性质.
2.复合函数的单调性:对于复合函数y=f[g(x)],若t=g(x)在区间(a,b)上是单调函数,且y=f(t)在区间(g(a),g(b))或者(g(b),g(a))上是单调函数,若t=g(x)与y=f(t)的单调性相同(同时为增或减),则y=f[g(x)]为增函数;若t=g(x)与y=f(t)的单调性相反,则y=f[g(x)]为减函数.简称:同增异减.
3.函数的值域常常化归为求函数的最值问题,要重视函数的单调性在确定函数最值过程中的应用.
易错辨析1——分段函数单调性的判定
[防范措施] 对于分段函数的单调性,有两种基本的判断方法:一保证各段上同增(减)时,要注意上、下段间端点值间的大小关系;二是画出这个分段函数的图象,结合函数图象、性质进行直观的判断.研究函数问题离不开函数图象,函数图象反映了函数的所有性质,在研究函数问题时要时时刻刻想到函数的图象,学会从函数图象上去分析问题、寻找解决问题的方法.
答案 C
