2.1.1 椭圆及其标准方程 课件 人教B版高中数学选修1-1(共21张PPT)
文档属性
| 名称 | 2.1.1 椭圆及其标准方程 课件 人教B版高中数学选修1-1(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 14:17:02 | ||
图片预览





文档简介
(共21张PPT)
生活中的椭圆
拱桥的桥拱采用基于椭圆的优化设计,
无论从力学原理,还是从施工角度考虑
都是优越于传统的圆弧型和抛物线型的。
中国水利水电科学研究院研究表明:
F1
F2
二.讲授新课:
1
.椭圆定义:
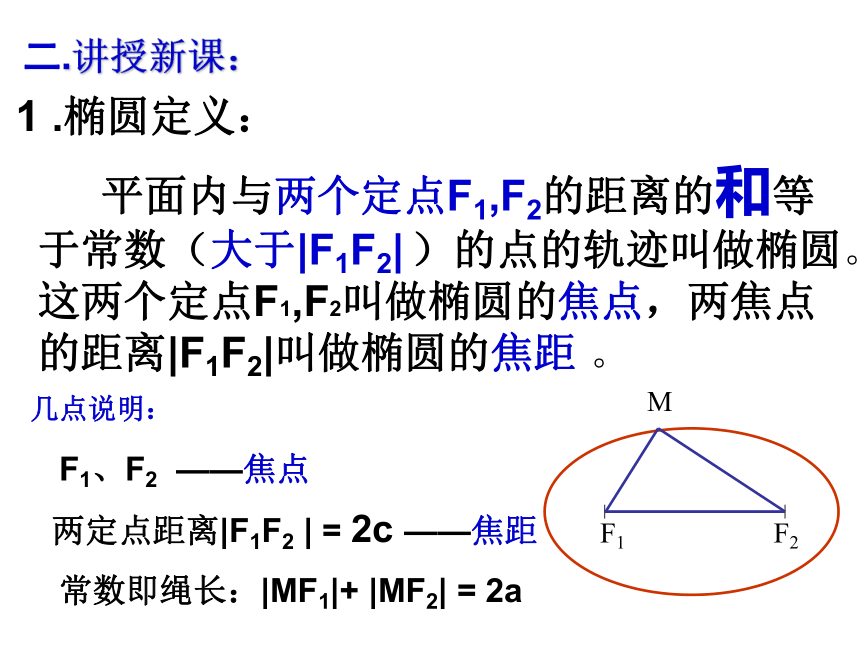
两定点距离|F1F2
|
=
2c
——焦距
常数即绳长:|MF1|+
|MF2|
=
2a
F1、F2
——焦点
平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|
)的点的轨迹叫做椭圆。这两个定点F1,F2叫做椭圆的焦点,两焦点的距离|F1F2|叫做椭圆的焦距
。
几点说明:
F1
F2
M
1.
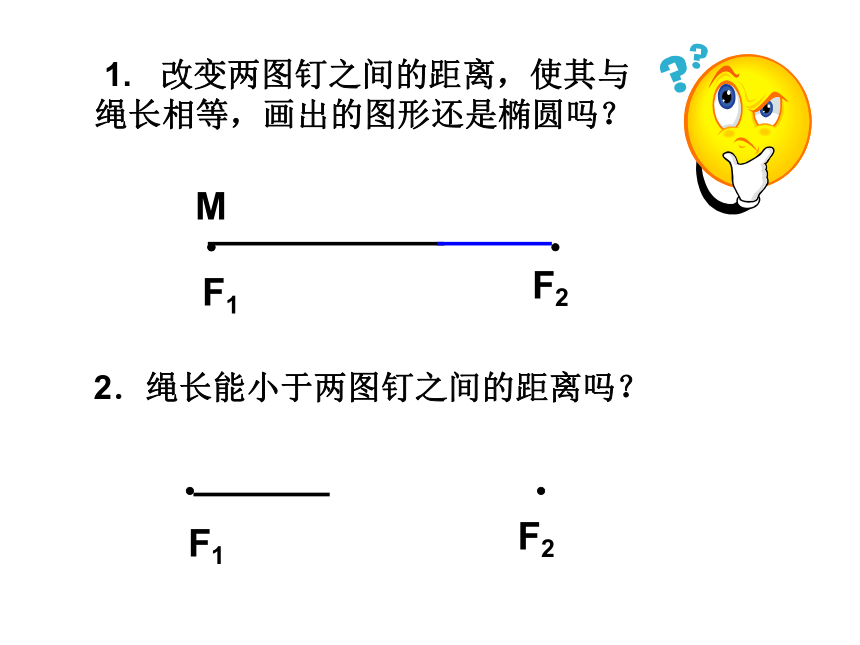
改变两图钉之间的距离,使其与绳长相等,画出的图形还是椭圆吗?
2.绳长能小于两图钉之间的距离吗?
F1
F2
M
F1
F2
练习1:动点P到两定点F1(-4,0),F2(4,0)的距离之和为8,则动点P的轨迹为
A.椭圆
B.线段F1F2
C.直线F1F2
D.不能确定
B
1.建系设点
2、椭圆的标准方程
已知椭圆的焦距为2c(c>0),M与F1、F2的距离的和为2a,其中a>c>0
2.列方程:
|MF1|+
|MF2|=2a
M
3.化简
移项
平方
整理
平方
整理
此即为焦点在x轴上的椭圆的标准方程
O
X
y
F1
F2
(0,-c)
(0
,
c)
椭圆的标准方程的再认识:
(1)椭圆标准方程的形式:左边是两个式子的平方和,右边是1
(2)标准方程中,常数a、b满足a2=b2+c2且a>b>0
(3)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪
一个轴上
练习2、填空:
(1)已知椭圆的方程为:
,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则三角形F2CD的周长为________
5
4
3
(3,0)、(-3,0)
6
20
F1
F2
C
D
(2)已知椭圆的方程为:
,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________;曲线上一点P到焦点F1的距离为3,则点P到另一个焦点F2的距离等于_________,则三角形F1PF2的周长为___________
2
3
3
(0,-
)、(0,
)
例1.
求适合下列条件的椭圆的标准方程.
(1)
a=3,b=1
焦点在x轴上
变式1:a=3,b=1
焦点在y
轴上
变式2:
a=3,b=1
三、例题讲解
(2)已知椭圆的两个焦点的坐标分别是(-3,0),(3,0),椭圆上一点到两焦点距离的和等于8,求椭圆的标准方程.
变式3:已知椭圆的两个焦点的坐标分别是
(0,3),(0,-3),椭圆上一点到两焦点距离的和等于8,求椭圆的标准方程.
例1:
求适合下列条件的椭圆的标准方程:
(3)
两个焦点的坐标分别是(0,3)、
(0,-3),并且椭圆经过点(0,5)
例1:
求适合下列条件的椭圆的标准方程:
例2:
三角形ABC两个顶点坐标是A(-4,0),B(4,0),周长是18,求顶点C的轨迹方程。
1、本节课你学习了哪些知识?
2、你掌握了什么?有哪些收获?
必做题:课后巩固作业
选做题:P38~练习B
1,2
图
形
方
程
焦
点
F(±c,0)
F(0,±c)
a,b,c之间的关系
a2=b2+c2
|MF1|+|MF2|=2a
(2a>2c>0)
定
义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
焦点位置的判断方法
椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上
生活中的椭圆
拱桥的桥拱采用基于椭圆的优化设计,
无论从力学原理,还是从施工角度考虑
都是优越于传统的圆弧型和抛物线型的。
中国水利水电科学研究院研究表明:
F1
F2
二.讲授新课:
1
.椭圆定义:
两定点距离|F1F2
|
=
2c
——焦距
常数即绳长:|MF1|+
|MF2|
=
2a
F1、F2
——焦点
平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|
)的点的轨迹叫做椭圆。这两个定点F1,F2叫做椭圆的焦点,两焦点的距离|F1F2|叫做椭圆的焦距
。
几点说明:
F1
F2
M
1.
改变两图钉之间的距离,使其与绳长相等,画出的图形还是椭圆吗?
2.绳长能小于两图钉之间的距离吗?
F1
F2
M
F1
F2
练习1:动点P到两定点F1(-4,0),F2(4,0)的距离之和为8,则动点P的轨迹为
A.椭圆
B.线段F1F2
C.直线F1F2
D.不能确定
B
1.建系设点
2、椭圆的标准方程
已知椭圆的焦距为2c(c>0),M与F1、F2的距离的和为2a,其中a>c>0
2.列方程:
|MF1|+
|MF2|=2a
M
3.化简
移项
平方
整理
平方
整理
此即为焦点在x轴上的椭圆的标准方程
O
X
y
F1
F2
(0,-c)
(0
,
c)
椭圆的标准方程的再认识:
(1)椭圆标准方程的形式:左边是两个式子的平方和,右边是1
(2)标准方程中,常数a、b满足a2=b2+c2且a>b>0
(3)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪
一个轴上
练习2、填空:
(1)已知椭圆的方程为:
,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则三角形F2CD的周长为________
5
4
3
(3,0)、(-3,0)
6
20
F1
F2
C
D
(2)已知椭圆的方程为:
,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________;曲线上一点P到焦点F1的距离为3,则点P到另一个焦点F2的距离等于_________,则三角形F1PF2的周长为___________
2
3
3
(0,-
)、(0,
)
例1.
求适合下列条件的椭圆的标准方程.
(1)
a=3,b=1
焦点在x轴上
变式1:a=3,b=1
焦点在y
轴上
变式2:
a=3,b=1
三、例题讲解
(2)已知椭圆的两个焦点的坐标分别是(-3,0),(3,0),椭圆上一点到两焦点距离的和等于8,求椭圆的标准方程.
变式3:已知椭圆的两个焦点的坐标分别是
(0,3),(0,-3),椭圆上一点到两焦点距离的和等于8,求椭圆的标准方程.
例1:
求适合下列条件的椭圆的标准方程:
(3)
两个焦点的坐标分别是(0,3)、
(0,-3),并且椭圆经过点(0,5)
例1:
求适合下列条件的椭圆的标准方程:
例2:
三角形ABC两个顶点坐标是A(-4,0),B(4,0),周长是18,求顶点C的轨迹方程。
1、本节课你学习了哪些知识?
2、你掌握了什么?有哪些收获?
必做题:课后巩固作业
选做题:P38~练习B
1,2
图
形
方
程
焦
点
F(±c,0)
F(0,±c)
a,b,c之间的关系
a2=b2+c2
|MF1|+|MF2|=2a
(2a>2c>0)
定
义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
焦点位置的判断方法
椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上
