2.2.2 双曲线的几何性质 人教B版高中数学选修1-1(共22张PPT)
文档属性
| 名称 | 2.2.2 双曲线的几何性质 人教B版高中数学选修1-1(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
定
义
标
准
方
程
焦
点
a.b.c的关系
F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭
圆
双曲线
F(0,±c)
F(0,±c)
一、复习回顾
o
Y
X
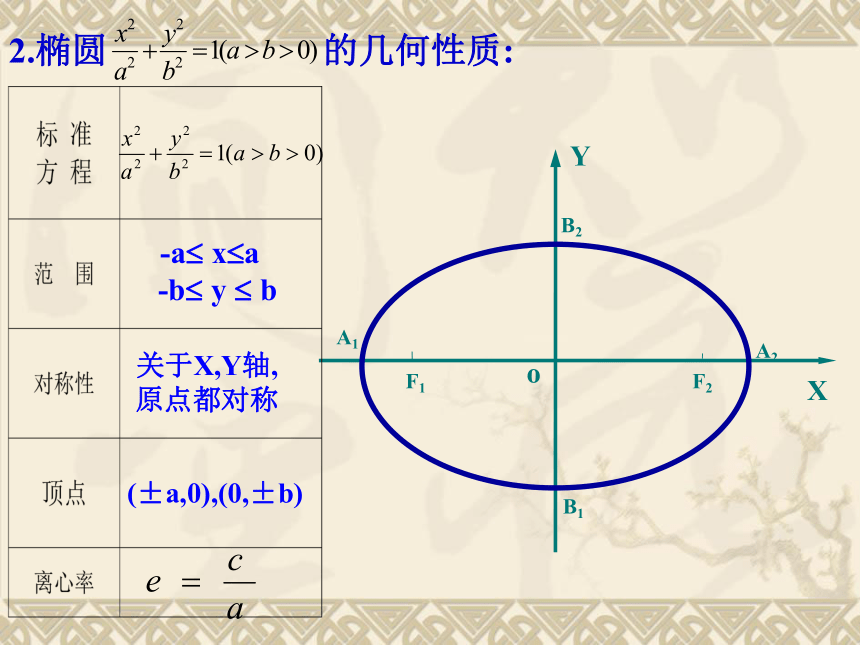
关于X,Y轴,
原点都对称
(±a,0),(0,±b)
-a?
x?a
-b?
y
?
b
F1
F2
A1
A2
B2
B1
2.椭圆
的几何性质:
(2)对称性
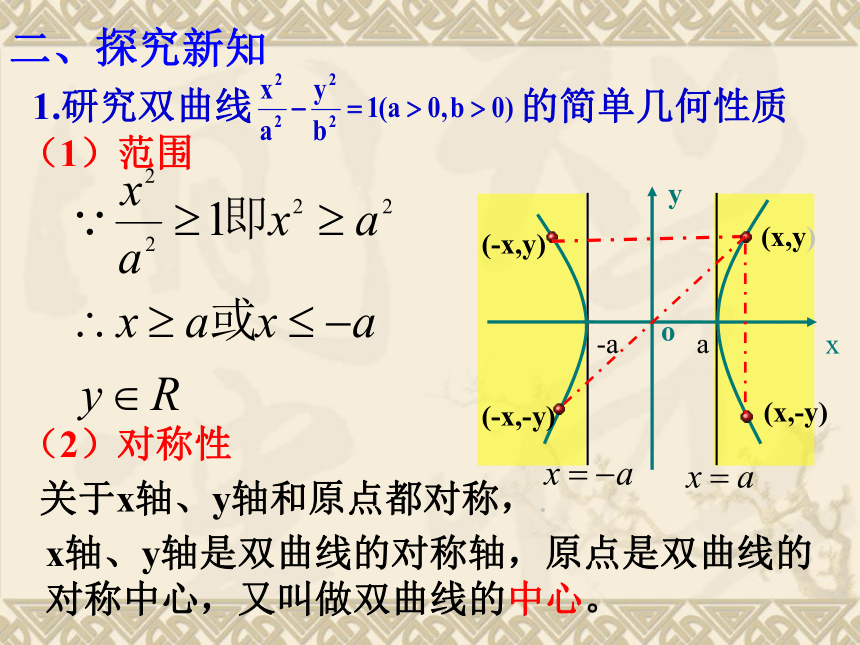
1.研究双曲线
的简单几何性质
(1)范围
关于x轴、y轴和原点都对称,.
x轴、y轴是双曲线的对称轴,原点是双曲线的对称中心,又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
二、探究新知
(3)顶点
①双曲线与对称轴的交点,叫做双曲线的顶点。
x
y
o
如图,线段
叫做双曲线的实轴,它的长为2a,a叫做双曲线的半实轴长;线段
叫做双曲线的虚轴,它的长为2b,b叫做双曲线的半虚轴长。
②
实轴与虚轴等长的双曲线
叫等轴双曲线。
③
(0,-b)
(0,b)
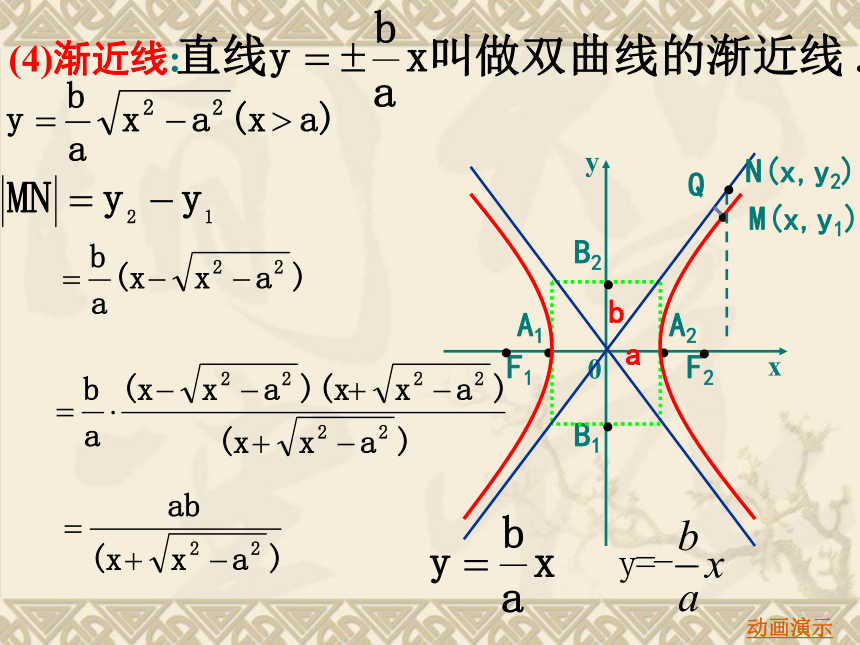
(4)渐近线:
动画演示
F1
F2
0
x
y
A1
A2
B2
B1
b
a
N(x,y2)
Q
M(x,y1)
注意:
(1)明确双曲线的渐近线是哪两条直线,是过双曲线实轴的两个端点与虚轴的两个端点分别作对称轴的平行线,它们围成一个矩形,其两条对角线所在直线即为双曲线的渐近线。画双曲线时,可先画出它的渐近线。
(2)理解“渐近”两字的含义。当双曲线的各支向外
延伸时,与这两条直线逐渐接近,但永不相交.
答:等轴双曲线的渐近线方程为:y=±x,
这两条直线互相垂直.
问题2.如何巧记忆双曲线的渐近线方程?
思考:
问题1.等轴双曲线的渐近线方程是什么?
这两条直线有什么位置关系?
练习:
求下列双曲线的渐近线方程
(5)离心率
离心率。
c>a>0
e
>1
e是反映双曲线张口大小的一个量,e越大张口越大!
①定义:
②e的范围:
③e的几何意义
:
动画演示
问题1.等轴双曲线的离心率e=
问题3.在双曲线中相关参数有哪些?
思考:
问题2.离心率是
的双曲线是什么双曲线?
(等轴双曲线)
关于x轴、y轴、原点对称
A1(-
a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
渐近线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
x
B1
y
O
.
F2
F1
B2
A1
A2
.
例1
:求双曲线
的半实轴长,半虚轴长,
焦点坐标,离心率和渐近线方程。
解:方程化为标准方程:
可得:半实轴长是4
半虚轴长是3
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
4
5
=
=
a
c
e
三、例题讲解
所以:a=4,b=3,c=
5
3
4
2
2
=
+
变式练习:
巩固练习
1.求符合下列条件的双曲线的标准方程:
2.等轴双曲线的一个焦点是F(-6,0),求它的标准方程和渐近线方程。
巩固练习
四、课堂小结
关于x轴、y轴、原点对称
A1(-
a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
渐近线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
x
B1
y
O
.
F2
F1
B2
A1
A2
.
四、课堂小结
五、课后作业
教材:54页A组2,3,4
定
义
标
准
方
程
焦
点
a.b.c的关系
F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭
圆
双曲线
F(0,±c)
F(0,±c)
一、复习回顾
o
Y
X
关于X,Y轴,
原点都对称
(±a,0),(0,±b)
-a?
x?a
-b?
y
?
b
F1
F2
A1
A2
B2
B1
2.椭圆
的几何性质:
(2)对称性
1.研究双曲线
的简单几何性质
(1)范围
关于x轴、y轴和原点都对称,.
x轴、y轴是双曲线的对称轴,原点是双曲线的对称中心,又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
二、探究新知
(3)顶点
①双曲线与对称轴的交点,叫做双曲线的顶点。
x
y
o
如图,线段
叫做双曲线的实轴,它的长为2a,a叫做双曲线的半实轴长;线段
叫做双曲线的虚轴,它的长为2b,b叫做双曲线的半虚轴长。
②
实轴与虚轴等长的双曲线
叫等轴双曲线。
③
(0,-b)
(0,b)
(4)渐近线:
动画演示
F1
F2
0
x
y
A1
A2
B2
B1
b
a
N(x,y2)
Q
M(x,y1)
注意:
(1)明确双曲线的渐近线是哪两条直线,是过双曲线实轴的两个端点与虚轴的两个端点分别作对称轴的平行线,它们围成一个矩形,其两条对角线所在直线即为双曲线的渐近线。画双曲线时,可先画出它的渐近线。
(2)理解“渐近”两字的含义。当双曲线的各支向外
延伸时,与这两条直线逐渐接近,但永不相交.
答:等轴双曲线的渐近线方程为:y=±x,
这两条直线互相垂直.
问题2.如何巧记忆双曲线的渐近线方程?
思考:
问题1.等轴双曲线的渐近线方程是什么?
这两条直线有什么位置关系?
练习:
求下列双曲线的渐近线方程
(5)离心率
离心率。
c>a>0
e
>1
e是反映双曲线张口大小的一个量,e越大张口越大!
①定义:
②e的范围:
③e的几何意义
:
动画演示
问题1.等轴双曲线的离心率e=
问题3.在双曲线中相关参数有哪些?
思考:
问题2.离心率是
的双曲线是什么双曲线?
(等轴双曲线)
关于x轴、y轴、原点对称
A1(-
a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
渐近线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
x
B1
y
O
.
F2
F1
B2
A1
A2
.
例1
:求双曲线
的半实轴长,半虚轴长,
焦点坐标,离心率和渐近线方程。
解:方程化为标准方程:
可得:半实轴长是4
半虚轴长是3
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
4
5
=
=
a
c
e
三、例题讲解
所以:a=4,b=3,c=
5
3
4
2
2
=
+
变式练习:
巩固练习
1.求符合下列条件的双曲线的标准方程:
2.等轴双曲线的一个焦点是F(-6,0),求它的标准方程和渐近线方程。
巩固练习
四、课堂小结
关于x轴、y轴、原点对称
A1(-
a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
渐近线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
x
B1
y
O
.
F2
F1
B2
A1
A2
.
四、课堂小结
五、课后作业
教材:54页A组2,3,4
