2.3.2 抛物线的几何性质 课件 人教B版高中数学选修1-1(共20张PPT)
文档属性
| 名称 | 2.3.2 抛物线的几何性质 课件 人教B版高中数学选修1-1(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 703.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 14:33:37 | ||
图片预览







文档简介
(共20张PPT)
抛物线的几何性质
学习目标
1.掌握抛物线的几何性质:范围、对称性、顶点、离心率、开口方向;
2.会利用抛物线的几何性质求抛物线的标准方程、焦点坐标及弦长问题;
.
F
M
.
1、抛物线的定义:
我们把平面内与一个定点
和一条定直线
的距离相等的点的轨迹叫做抛物线,点
叫做抛物线的焦点,直线
叫做抛物线的准线.
抛物线
的
焦点坐标是:
准线方程为:
图
形
方
程
焦
点
准
线
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2
=
2px
(p>0)
y2
=
-2px
(p>0)
x2
=
2py
(p>0)
x2
=
-2py
(p>0)
P(x,y)
一、抛物线的几何性质
抛物线在y轴的右侧,当x的值增大时,︱y︱也增大,这说明抛物线向右上方和右下方无限延伸。
1、范围
由抛物线y2
=2px(p>0)
而
所以抛物线的范围为
关于x轴
对称
由于点
也满
足
,故抛物线
(p>0)关于x轴对称.
y2
=
2px
y2
=
2px
2、对称性
P(x,y)
定义:抛物线和它的轴的交点称为抛物线
的顶点。
P(x,y)
由y2
=
2px
(p>0)当y=0时,x=0,
因此抛物线的顶点就是坐标原点(0,0)。
注:这与椭圆有四个顶点,双曲线有两个顶点不同。
3、顶点
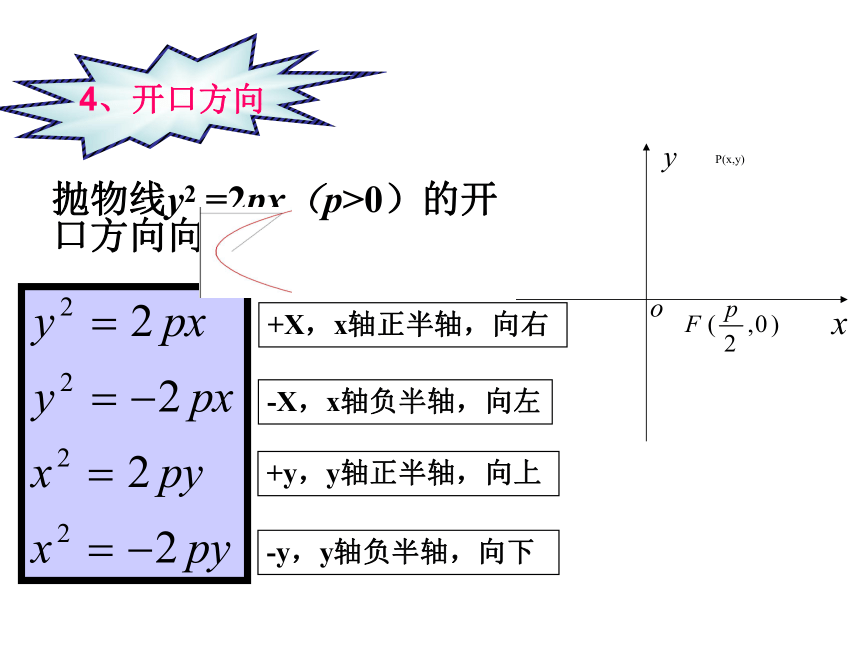
4、开口方向
P(x,y)
抛物线y2
=2px(p>0)的开口方向向右。
+X,x轴正半轴,向右
-X,x轴负半轴,向左
+y,y轴正半轴,向上
-y,y轴负半轴,向下
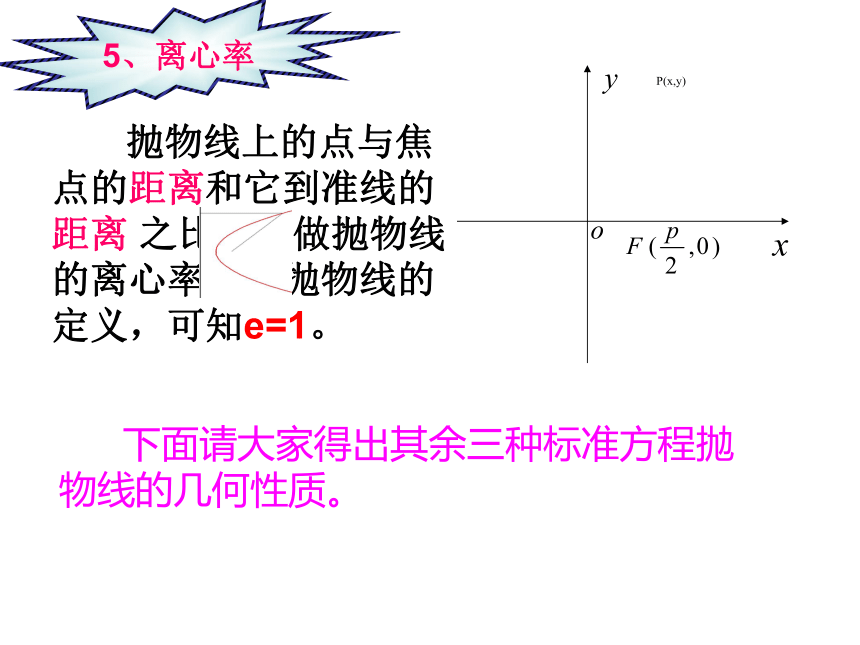
5、离心率
P(x,y)
抛物线上的点与焦点的距离和它到准线的距离
之比,叫做抛物线的离心率,由抛物线的定义,可知e=1。
下面请大家得出其余三种标准方程抛物线的几何性质。
(二)归纳:抛物线的几何性质
图
形
方程
焦点
准线
范围
顶点
对称轴
e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2
=
2px
(p>0)
y2
=
-2px
(p>0)
x2
=
2py
(p>0)
x2
=
-2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y
≤
0
x∈R
(0,0)
x轴
y轴
1
特点:
1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;
2.抛物线只有一条对称轴,没有
对称中心;
3.抛物线只有一个顶点、
一个焦点、一条准线;
4.抛物线的离心率是确定的,为1;
思考:抛物线标准方程中的p
对抛物线开口的影响.
P(x,y)
例1:已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程。
因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),
解:
所以设方程为:
又因为点M在抛物线上:
所以:
因此所求抛物线标准方程为:
(三)、例题讲解:
题型一
求抛物线的方程
变式训练1
顶点在坐标原点,对称轴是坐标轴,并且经过点M(2,
)的抛物线的方程有几条?并求出它们的标准方程。
顶点在坐标原点,对称轴是坐标轴,并且经过点M(2,
)的抛物线的方程有几条?并求出它们的标准方程。
顶点在坐标原点,对称轴是坐标轴,并且经过点M(2,
)的抛物线的方程有几条?并求出它们的标准方程。
顶点在坐标原点,对称轴是坐标轴,并且经过点M(2,
)的抛物线的方程有几条?并求出它们的标准方程。
变式训练2:
已知抛物线y2=4x截直线y=x+b所得弦长为4,求b的值.
当堂检测:
1、求适合下列条件的抛物线的方程:
(1)顶点在原点,焦点F为(0,5).
(2)顶点在原点,准线是x=4.
(3)
顶点在原点,关于x轴对称,并且
经过点M(5,-4).
(4)
焦点F为(0,-8),准线是y=8.
y2=-16x
x2=-32y
2、过抛物线
的焦点,作倾斜角为
的直线,则被抛物线截得的弦长为
;
已知抛物线y2=2x,过点Q(2,1)
作斜率为1直线交抛物线于A、B两点,
试求弦AB的中点M。
3、
依照上题的思路:xA+xB=4
所以xM=2
将xM=2代入
y=x-1得yM=1
所以M为(2,1)
(三):课堂小结
1:知识小结
2:方法小结
3:布置作业:
书面作业:课本第64页第1,2,3,4题;
08.12.1
抛物线的几何性质
学习目标
1.掌握抛物线的几何性质:范围、对称性、顶点、离心率、开口方向;
2.会利用抛物线的几何性质求抛物线的标准方程、焦点坐标及弦长问题;
.
F
M
.
1、抛物线的定义:
我们把平面内与一个定点
和一条定直线
的距离相等的点的轨迹叫做抛物线,点
叫做抛物线的焦点,直线
叫做抛物线的准线.
抛物线
的
焦点坐标是:
准线方程为:
图
形
方
程
焦
点
准
线
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2
=
2px
(p>0)
y2
=
-2px
(p>0)
x2
=
2py
(p>0)
x2
=
-2py
(p>0)
P(x,y)
一、抛物线的几何性质
抛物线在y轴的右侧,当x的值增大时,︱y︱也增大,这说明抛物线向右上方和右下方无限延伸。
1、范围
由抛物线y2
=2px(p>0)
而
所以抛物线的范围为
关于x轴
对称
由于点
也满
足
,故抛物线
(p>0)关于x轴对称.
y2
=
2px
y2
=
2px
2、对称性
P(x,y)
定义:抛物线和它的轴的交点称为抛物线
的顶点。
P(x,y)
由y2
=
2px
(p>0)当y=0时,x=0,
因此抛物线的顶点就是坐标原点(0,0)。
注:这与椭圆有四个顶点,双曲线有两个顶点不同。
3、顶点
4、开口方向
P(x,y)
抛物线y2
=2px(p>0)的开口方向向右。
+X,x轴正半轴,向右
-X,x轴负半轴,向左
+y,y轴正半轴,向上
-y,y轴负半轴,向下
5、离心率
P(x,y)
抛物线上的点与焦点的距离和它到准线的距离
之比,叫做抛物线的离心率,由抛物线的定义,可知e=1。
下面请大家得出其余三种标准方程抛物线的几何性质。
(二)归纳:抛物线的几何性质
图
形
方程
焦点
准线
范围
顶点
对称轴
e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2
=
2px
(p>0)
y2
=
-2px
(p>0)
x2
=
2py
(p>0)
x2
=
-2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y
≤
0
x∈R
(0,0)
x轴
y轴
1
特点:
1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;
2.抛物线只有一条对称轴,没有
对称中心;
3.抛物线只有一个顶点、
一个焦点、一条准线;
4.抛物线的离心率是确定的,为1;
思考:抛物线标准方程中的p
对抛物线开口的影响.
P(x,y)
例1:已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程。
因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),
解:
所以设方程为:
又因为点M在抛物线上:
所以:
因此所求抛物线标准方程为:
(三)、例题讲解:
题型一
求抛物线的方程
变式训练1
顶点在坐标原点,对称轴是坐标轴,并且经过点M(2,
)的抛物线的方程有几条?并求出它们的标准方程。
顶点在坐标原点,对称轴是坐标轴,并且经过点M(2,
)的抛物线的方程有几条?并求出它们的标准方程。
顶点在坐标原点,对称轴是坐标轴,并且经过点M(2,
)的抛物线的方程有几条?并求出它们的标准方程。
顶点在坐标原点,对称轴是坐标轴,并且经过点M(2,
)的抛物线的方程有几条?并求出它们的标准方程。
变式训练2:
已知抛物线y2=4x截直线y=x+b所得弦长为4,求b的值.
当堂检测:
1、求适合下列条件的抛物线的方程:
(1)顶点在原点,焦点F为(0,5).
(2)顶点在原点,准线是x=4.
(3)
顶点在原点,关于x轴对称,并且
经过点M(5,-4).
(4)
焦点F为(0,-8),准线是y=8.
y2=-16x
x2=-32y
2、过抛物线
的焦点,作倾斜角为
的直线,则被抛物线截得的弦长为
;
已知抛物线y2=2x,过点Q(2,1)
作斜率为1直线交抛物线于A、B两点,
试求弦AB的中点M。
3、
依照上题的思路:xA+xB=4
所以xM=2
将xM=2代入
y=x-1得yM=1
所以M为(2,1)
(三):课堂小结
1:知识小结
2:方法小结
3:布置作业:
书面作业:课本第64页第1,2,3,4题;
08.12.1
