2.3.1 抛物线 人教B版高中数学选修1-1 第二章圆锥曲线与方程(共39张PPT)
文档属性
| 名称 | 2.3.1 抛物线 人教B版高中数学选修1-1 第二章圆锥曲线与方程(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 14:35:20 | ||
图片预览









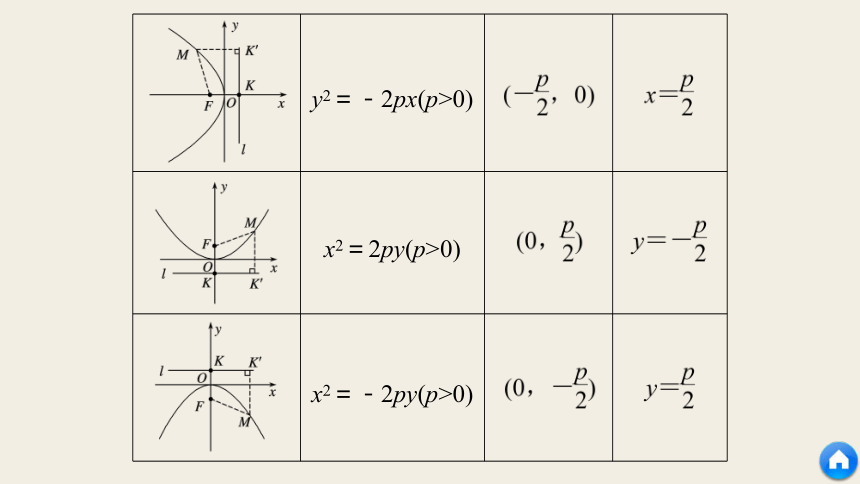


文档简介
(共39张PPT)
第二章 §2.4 抛物线
2.4.1 抛物线及其标准方程
学习目标
1.掌握抛物线的定义及焦点、准线的概念.
2.掌握抛物线的标准方程及其推导.
3.明确抛物线标准方程中p的几何意义,并能解决简单的求抛物线标准方程问题.
题型探究
问题导学
内容索引
当堂训练
问题导学
知识点一 抛物线的定义
思考1
平面内,到两定点距离相等的点的轨迹是什么?
连接两定点所得线段的垂直平分线.
答案
思考2
平面内,到两个确定平行直线l1,l2距离相等的点的轨迹是什么?
一条直线.
答案
思考3
到定点的距离与到定直线的距离相等的点的轨迹是什么?
抛物线.
答案
梳理
(1)平面内与一个定点F和一条定直线l(l不经过点F)距离
的点的轨迹叫做抛物线.点F叫做抛物线的
,直线l叫做抛物线的
.
(2)定义的实质可归纳为“一动三定”:一个动点,设为M;一个定点F(抛物线的焦点);一条定直线(抛物线的准线);一个定值(即点M到点F的距离与它到定直线l的距离之比等于1∶1).
准线
相等
焦点
知识点二 抛物线的标准方程
思考
抛物线的标准方程有何特点?
(1)以方程的解为坐标的点在抛物线上;
(2)对称轴为坐标轴;
(3)p为大于0的常数,其几何意义表示焦点到准线的距离;
(4)准线与对称轴垂直,垂足与焦点关于原点对称;
(5)焦点、准线到原点的距离都等于
.
答案
梳理
由于抛物线焦点位置不同,方程也就不同,故抛物线的标准方程有以下几种形式:y2=2px(p>0),y2=-2px(p>0),x2=2py(p>0),x2=-2py(p>0).
现将这四种抛物线对应的图形、标准方程、焦点坐标及准线方程列表如下:
图形
标准方程
焦点坐标
准线方程
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
题型探究
类型一 抛物线的定义及理解
设动点M(x,y),上式可看作动点M到原点的距离等于动点M到直线3x+4y-12=0的距离,所以动点M的轨迹是以原点为焦点,以直线3x+4y-12=0为准线的抛物线.
A.椭圆
B.双曲线
C.抛物线
D.以上都不对
答案
解析
设动点Q(x′,y′),则有x′=x+y,y′=xy,又有x2+y2=1,即(x+y)2-2xy=1,所以x′2-2y′=1,故Q(x+y,xy)的轨迹所在的曲线是抛物线.
(2)已知点P(x,y)在以原点为圆心的单位圆x2+y2=1上运动,则点Q(x+y,xy)的轨迹所在的曲线是_______.(在圆、抛物线、椭圆、双曲线中选择一个作答)
答案
解析
抛物线
抛物线的判断方法
(1)可以看动点是否符合抛物线的定义,即到定点的距离等于到定直线(直线不过定点)的距离.
(2)求出动点的轨迹方程,看方程是否符合抛物线的方程.
反思与感悟
跟踪训练1 平面上动点P到定点F(1,0)的距离比点P到y轴的距离大1,求动点P的轨迹方程.
解答
方法一 设点P的坐标为(x,y),
两边平方并化简得y2=2x+2|x|.
方法二 由题意,动点P到定点F(1,0)的距离比到y轴的距离大1,
由于点F(1,0)到y轴的距离为1,
故当x<0时,直线y=0上的点适合条件;
当x≥0时,原命题等价于点P到点F(1,0)与到直线x=-1的距离相等,
故点P的轨迹是以F为焦点,x=-1为准线的抛物线,方程为y2=4x.
类型二 抛物线标准方程及求解
命题角度1 抛物线的焦点坐标或准线方程的求解
答案
解析
根据抛物线方程求准线方程或焦点坐标时,应先把抛物线的方程化为标准方程,即等式左端是二次项且系数是1,等式右端是一次项,这样才能准确写出抛物线的准线方程.
反思与感悟
因为抛物线的焦点坐标为(1,0),
跟踪训练2 (1)若抛物线y2=2px的焦点坐标为(1,0),则p=___;准线方程为_______.
2
x=-1
答案
解析
焦点坐标为(10,0),准线方程为x=-10.
(2)求下列抛物线的焦点坐标和准线方程.
①y2=40x;
解答
②4x2=y;
解答
③3y2=5x;
解答
④6y2+11x=0.
解答
左顶点为(-3,0),
∴p=6,∴抛物线的方程为y2=-12x.
命题角度2 求解抛物线的标准方程
例3 根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
解答
设所求焦点在x轴上的抛物线的方程为y2=2px(p≠0),A(m,-3),
又(-3)2=2pm,∴p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
解答
抛物线标准方程的求法
(1)定义法:建立适当坐标系,利用抛物线的定义列出动点满足的条件,列出方程,进行化简,根据定义求出p,最后写出标准方程.
(2)待定系数法:由于标准方程有四种形式,因而在求方程时应首先确定焦点在哪一个半轴上,进而确定方程的形式,然后再利用已知条件确定p的值.
反思与感悟
设抛物线方程为y2=-2px(p>0),
抛物线的焦点坐标为(-2,0),准线方程为x=2.
跟踪训练3 已知抛物线的顶点在原点,对称轴为x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和m的值,并写出抛物线的焦点坐标和准线方程.
解答
类型三 抛物线在实际生活中的应用
例4 河上有一抛物线形拱桥,当水面距拱桥顶5
m时,水面宽为8
m,一小船宽4
m、高2
m,载货后船露出水面上的部分高0.75
m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
解答
反思与感悟
涉及拱桥、隧道的问题,通常需建立适当的平面直角坐标系,利用抛物线的标准方程进行求解.
跟踪训练4 喷灌的喷头装在直立管柱OA的顶点A处,喷出水流的最高点B高5
m,且与OA所在的直线相距4
m,水流落在以O为圆心,半径为9
m的圆上,则管柱OA的长是多少?
解答
如图所示,建立直角坐标系,设水流所形成的抛物线的方程为x2=-2py(p>0),
因为点C(5,-5)在抛物线上,所以25=-2p·(-5),因此2p=5,所以抛物线的方程为x2=-5y,点A(-4,y0)在抛物线上,
所以管柱OA的长为1.8
m.
当堂训练
答案
解析
A.y=-1
B.y=-2
C.x=-1
D.x=-2
√
2
3
4
5
1
2.已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-2)到焦点的距离为4,则m的值为
A.4
B.-2
C.4或-4
D.12或-2
由题可设抛物线的标准方程为x2=-2py(p>0),由定义知点P到准线的距
离为4,故
+2=4,∴p=4,∴x2=-8y.将点P的坐标代入x2=-8y,
得m=±4.
答案
解析
√
2
3
4
5
1
2
3
4
5
1
因为抛物线上的动点到焦点的距离为动点到准线的距离,所以抛物线上
的动点到焦点的最短距离为顶点到准线的距离,即
=1,p=2.
3.若抛物线y2=2px(p>0)上的动点Q到焦点的距离的最小值为1,则p=___.
2
答案
解析
4.若抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的一个焦点,则p=_____.
2
3
4
5
1
答案
解析
5.已知M为抛物线y2=4x上一动点,F为抛物线的焦点,定点N(2,3),则|MN|+|MF|的最小值为_____.
答案
解析
2
3
4
5
1
规律与方法
3.对于抛物线上的点,利用定义可以把其到焦点的距离转化为到准线的距离,也可以把其到准线的距离转化为到焦点的距离,因此可以解决有关距离的最值问题.
本课结束
第二章 §2.4 抛物线
2.4.1 抛物线及其标准方程
学习目标
1.掌握抛物线的定义及焦点、准线的概念.
2.掌握抛物线的标准方程及其推导.
3.明确抛物线标准方程中p的几何意义,并能解决简单的求抛物线标准方程问题.
题型探究
问题导学
内容索引
当堂训练
问题导学
知识点一 抛物线的定义
思考1
平面内,到两定点距离相等的点的轨迹是什么?
连接两定点所得线段的垂直平分线.
答案
思考2
平面内,到两个确定平行直线l1,l2距离相等的点的轨迹是什么?
一条直线.
答案
思考3
到定点的距离与到定直线的距离相等的点的轨迹是什么?
抛物线.
答案
梳理
(1)平面内与一个定点F和一条定直线l(l不经过点F)距离
的点的轨迹叫做抛物线.点F叫做抛物线的
,直线l叫做抛物线的
.
(2)定义的实质可归纳为“一动三定”:一个动点,设为M;一个定点F(抛物线的焦点);一条定直线(抛物线的准线);一个定值(即点M到点F的距离与它到定直线l的距离之比等于1∶1).
准线
相等
焦点
知识点二 抛物线的标准方程
思考
抛物线的标准方程有何特点?
(1)以方程的解为坐标的点在抛物线上;
(2)对称轴为坐标轴;
(3)p为大于0的常数,其几何意义表示焦点到准线的距离;
(4)准线与对称轴垂直,垂足与焦点关于原点对称;
(5)焦点、准线到原点的距离都等于
.
答案
梳理
由于抛物线焦点位置不同,方程也就不同,故抛物线的标准方程有以下几种形式:y2=2px(p>0),y2=-2px(p>0),x2=2py(p>0),x2=-2py(p>0).
现将这四种抛物线对应的图形、标准方程、焦点坐标及准线方程列表如下:
图形
标准方程
焦点坐标
准线方程
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
题型探究
类型一 抛物线的定义及理解
设动点M(x,y),上式可看作动点M到原点的距离等于动点M到直线3x+4y-12=0的距离,所以动点M的轨迹是以原点为焦点,以直线3x+4y-12=0为准线的抛物线.
A.椭圆
B.双曲线
C.抛物线
D.以上都不对
答案
解析
设动点Q(x′,y′),则有x′=x+y,y′=xy,又有x2+y2=1,即(x+y)2-2xy=1,所以x′2-2y′=1,故Q(x+y,xy)的轨迹所在的曲线是抛物线.
(2)已知点P(x,y)在以原点为圆心的单位圆x2+y2=1上运动,则点Q(x+y,xy)的轨迹所在的曲线是_______.(在圆、抛物线、椭圆、双曲线中选择一个作答)
答案
解析
抛物线
抛物线的判断方法
(1)可以看动点是否符合抛物线的定义,即到定点的距离等于到定直线(直线不过定点)的距离.
(2)求出动点的轨迹方程,看方程是否符合抛物线的方程.
反思与感悟
跟踪训练1 平面上动点P到定点F(1,0)的距离比点P到y轴的距离大1,求动点P的轨迹方程.
解答
方法一 设点P的坐标为(x,y),
两边平方并化简得y2=2x+2|x|.
方法二 由题意,动点P到定点F(1,0)的距离比到y轴的距离大1,
由于点F(1,0)到y轴的距离为1,
故当x<0时,直线y=0上的点适合条件;
当x≥0时,原命题等价于点P到点F(1,0)与到直线x=-1的距离相等,
故点P的轨迹是以F为焦点,x=-1为准线的抛物线,方程为y2=4x.
类型二 抛物线标准方程及求解
命题角度1 抛物线的焦点坐标或准线方程的求解
答案
解析
根据抛物线方程求准线方程或焦点坐标时,应先把抛物线的方程化为标准方程,即等式左端是二次项且系数是1,等式右端是一次项,这样才能准确写出抛物线的准线方程.
反思与感悟
因为抛物线的焦点坐标为(1,0),
跟踪训练2 (1)若抛物线y2=2px的焦点坐标为(1,0),则p=___;准线方程为_______.
2
x=-1
答案
解析
焦点坐标为(10,0),准线方程为x=-10.
(2)求下列抛物线的焦点坐标和准线方程.
①y2=40x;
解答
②4x2=y;
解答
③3y2=5x;
解答
④6y2+11x=0.
解答
左顶点为(-3,0),
∴p=6,∴抛物线的方程为y2=-12x.
命题角度2 求解抛物线的标准方程
例3 根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
解答
设所求焦点在x轴上的抛物线的方程为y2=2px(p≠0),A(m,-3),
又(-3)2=2pm,∴p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
解答
抛物线标准方程的求法
(1)定义法:建立适当坐标系,利用抛物线的定义列出动点满足的条件,列出方程,进行化简,根据定义求出p,最后写出标准方程.
(2)待定系数法:由于标准方程有四种形式,因而在求方程时应首先确定焦点在哪一个半轴上,进而确定方程的形式,然后再利用已知条件确定p的值.
反思与感悟
设抛物线方程为y2=-2px(p>0),
抛物线的焦点坐标为(-2,0),准线方程为x=2.
跟踪训练3 已知抛物线的顶点在原点,对称轴为x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和m的值,并写出抛物线的焦点坐标和准线方程.
解答
类型三 抛物线在实际生活中的应用
例4 河上有一抛物线形拱桥,当水面距拱桥顶5
m时,水面宽为8
m,一小船宽4
m、高2
m,载货后船露出水面上的部分高0.75
m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
解答
反思与感悟
涉及拱桥、隧道的问题,通常需建立适当的平面直角坐标系,利用抛物线的标准方程进行求解.
跟踪训练4 喷灌的喷头装在直立管柱OA的顶点A处,喷出水流的最高点B高5
m,且与OA所在的直线相距4
m,水流落在以O为圆心,半径为9
m的圆上,则管柱OA的长是多少?
解答
如图所示,建立直角坐标系,设水流所形成的抛物线的方程为x2=-2py(p>0),
因为点C(5,-5)在抛物线上,所以25=-2p·(-5),因此2p=5,所以抛物线的方程为x2=-5y,点A(-4,y0)在抛物线上,
所以管柱OA的长为1.8
m.
当堂训练
答案
解析
A.y=-1
B.y=-2
C.x=-1
D.x=-2
√
2
3
4
5
1
2.已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-2)到焦点的距离为4,则m的值为
A.4
B.-2
C.4或-4
D.12或-2
由题可设抛物线的标准方程为x2=-2py(p>0),由定义知点P到准线的距
离为4,故
+2=4,∴p=4,∴x2=-8y.将点P的坐标代入x2=-8y,
得m=±4.
答案
解析
√
2
3
4
5
1
2
3
4
5
1
因为抛物线上的动点到焦点的距离为动点到准线的距离,所以抛物线上
的动点到焦点的最短距离为顶点到准线的距离,即
=1,p=2.
3.若抛物线y2=2px(p>0)上的动点Q到焦点的距离的最小值为1,则p=___.
2
答案
解析
4.若抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的一个焦点,则p=_____.
2
3
4
5
1
答案
解析
5.已知M为抛物线y2=4x上一动点,F为抛物线的焦点,定点N(2,3),则|MN|+|MF|的最小值为_____.
答案
解析
2
3
4
5
1
规律与方法
3.对于抛物线上的点,利用定义可以把其到焦点的距离转化为到准线的距离,也可以把其到准线的距离转化为到焦点的距离,因此可以解决有关距离的最值问题.
本课结束
