3.1.3导数的几何意义 课件—人教B版高中数学选修1-1(共19张PPT)
文档属性
| 名称 | 3.1.3导数的几何意义 课件—人教B版高中数学选修1-1(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 14:37:57 | ||
图片预览





文档简介
(共19张PPT)
导数的几何意义
高二数学
选修1-1
一、复习回顾
1、割线的斜率
其几何意义表示曲线上两点连线(就是曲线的割线)的斜率。
瞬时变化率
二.思考
三.新课讲授
P
Pn
o
x
y
y=f(x)
割线
切线
T
2.切线的定义
结论:当割线PPn无限地趋近于某一极限位置PT,我们就把极限
位置上的直线PT,叫做曲线C在点P处的切线。
新授
思考
P
l
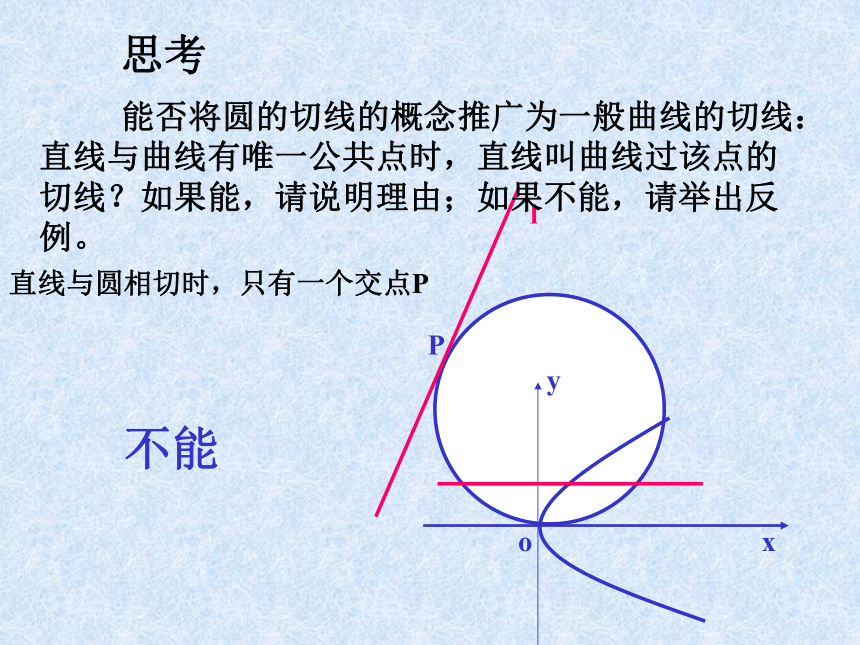
能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。
不能
x
y
o
直线与圆相切时,只有一个交点P
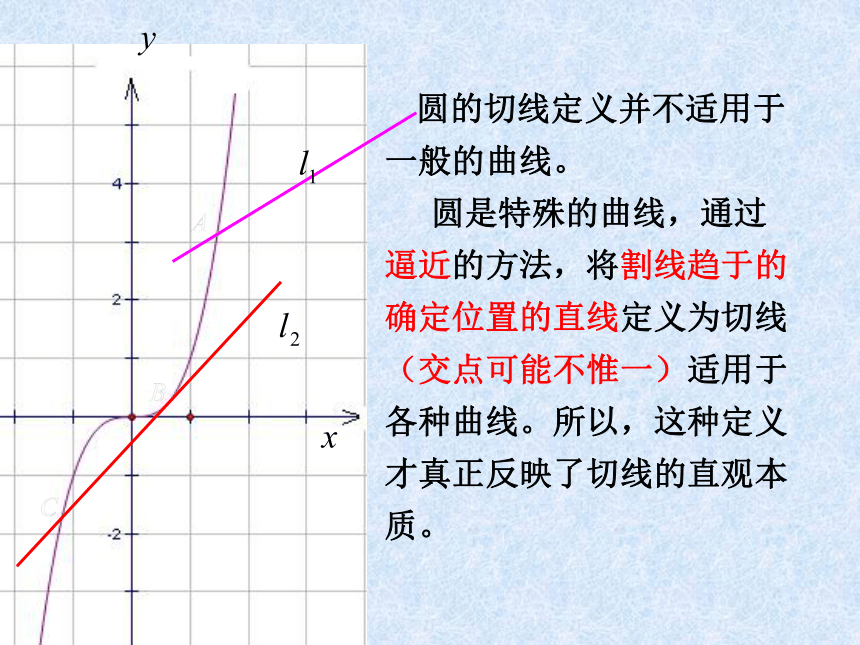
圆的切线定义并不适用于一般的曲线。
圆是特殊的曲线,通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
x
o
y
y=f(x)
P(x0,y0)
(x1,y1)
M
△x
△y
3.割线与切线的斜率有何关系呢?
关系:当△x→0时,割线PPn的斜率的极限,就是曲线在点P处的切线的斜率
4.导数的几何意义:
函数
在
处的导数的几何意义是曲线
在
处切线的斜率.
即
=
继续观察图像的运动过程,还有什么发现?
x
o
y
y=f(x)
P
Q1
Q2
Q3
Q4
T
四.典型例题
变式训练
如图,试描述函数y=f(x)在x=-3,-2,0,1附近的变化情况.
(1)函数f(x)在x=-3处切线斜率k>0,曲线是上升的.即函数f(x)在x=-3附近是单调递增
(2)函数f(x)在x=-2处切线的斜率k<0,曲线是下降的即函数f(x)在x=-2附近是单调递减
(3)函数f(x)在x=0处切线的斜率k接近于0,所以函数f(x)在x=0附近几乎没有变化,
(4)函数f(x)在x=1切线的斜率k>0,曲线是上升的.即函数f(x)在x=1附近是单调递增.
五.当堂检测
1.设f′(
)=0,则曲线y=f(x)在点(
,f(
))处的切线( )
A.不存在
B.与x轴平行或重合
C.与x轴垂直
D.与x轴斜交
2.如图,直线l是曲线y=f(x)在x=4处的切线,则f′(4)=
B
3.已知曲线y=f(x)在x=5处的切线方程是y=-x+8,则f(5)及f′(5)分别为
( )
A.3,3
B.3,-1
C.-1,3
D.-1,-1
4.曲线y=
-1在点(1,0)处的切线的斜率等于( )
A.-1
B.0
C.1
D.2
5.如果f(x)=
,那么f(x)在点x=
处的切线的倾斜角是________.
B
D
(1)函数
在
处的导数的几何意义是曲线
在
处切线的斜率.
即=
(3)数学思想:逼近的思想,以直代曲,数形结合
六.课堂小结
(4)总结:一图二义三思想。
本节课你收获了什么?
导数的几何意义
高二数学
选修1-1
一、复习回顾
1、割线的斜率
其几何意义表示曲线上两点连线(就是曲线的割线)的斜率。
瞬时变化率
二.思考
三.新课讲授
P
Pn
o
x
y
y=f(x)
割线
切线
T
2.切线的定义
结论:当割线PPn无限地趋近于某一极限位置PT,我们就把极限
位置上的直线PT,叫做曲线C在点P处的切线。
新授
思考
P
l
能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。
不能
x
y
o
直线与圆相切时,只有一个交点P
圆的切线定义并不适用于一般的曲线。
圆是特殊的曲线,通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
x
o
y
y=f(x)
P(x0,y0)
(x1,y1)
M
△x
△y
3.割线与切线的斜率有何关系呢?
关系:当△x→0时,割线PPn的斜率的极限,就是曲线在点P处的切线的斜率
4.导数的几何意义:
函数
在
处的导数的几何意义是曲线
在
处切线的斜率.
即
=
继续观察图像的运动过程,还有什么发现?
x
o
y
y=f(x)
P
Q1
Q2
Q3
Q4
T
四.典型例题
变式训练
如图,试描述函数y=f(x)在x=-3,-2,0,1附近的变化情况.
(1)函数f(x)在x=-3处切线斜率k>0,曲线是上升的.即函数f(x)在x=-3附近是单调递增
(2)函数f(x)在x=-2处切线的斜率k<0,曲线是下降的即函数f(x)在x=-2附近是单调递减
(3)函数f(x)在x=0处切线的斜率k接近于0,所以函数f(x)在x=0附近几乎没有变化,
(4)函数f(x)在x=1切线的斜率k>0,曲线是上升的.即函数f(x)在x=1附近是单调递增.
五.当堂检测
1.设f′(
)=0,则曲线y=f(x)在点(
,f(
))处的切线( )
A.不存在
B.与x轴平行或重合
C.与x轴垂直
D.与x轴斜交
2.如图,直线l是曲线y=f(x)在x=4处的切线,则f′(4)=
B
3.已知曲线y=f(x)在x=5处的切线方程是y=-x+8,则f(5)及f′(5)分别为
( )
A.3,3
B.3,-1
C.-1,3
D.-1,-1
4.曲线y=
-1在点(1,0)处的切线的斜率等于( )
A.-1
B.0
C.1
D.2
5.如果f(x)=
,那么f(x)在点x=
处的切线的倾斜角是________.
B
D
(1)函数
在
处的导数的几何意义是曲线
在
处切线的斜率.
即=
(3)数学思想:逼近的思想,以直代曲,数形结合
六.课堂小结
(4)总结:一图二义三思想。
本节课你收获了什么?
