2020-2021学年苏科版九年级数学下册6.4 探索三角形相似的条件 培优训练(Word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版九年级数学下册6.4 探索三角形相似的条件 培优训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 14:48:35 | ||
图片预览



文档简介
6.4探索三角形相似的条件(1)
一、选择题
1.(2019秋?梁溪区期末)如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.已知AB=1,BC=3,DE=1.2,则DF的长为( )
A.3.6 B.4.8 C.5 D.5.2
2.(2019秋?玄武区期末)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=1.5,BC=2,DE=1.8,则EF=( )
A.4.4 B.4 C.3.4 D.2.4
3.(2020春?锡山区期中)如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A. B. C. D.
4.(2020秋?惠山区校级月考)如图,l1∥l2∥l3,则下列等式错误的是( )
A. B. C. D.
5.(2020秋?朝阳区期中)如图,AB∥CD∥EF,AF与BE相交于点G.若AG=2,GD=1,DF=5,BC=4,则BE的长为( )
A. B. C.12 D.20
6.(2020秋?沈阳月考)如图,BE和CD是△ABC的中线,连接DE,则的值是( )
A. B. C. D.
7.(2020?雨花区校级一模)如图,直线a∥b∥c,则下列结论不正确的为( )
A. B. C. D.
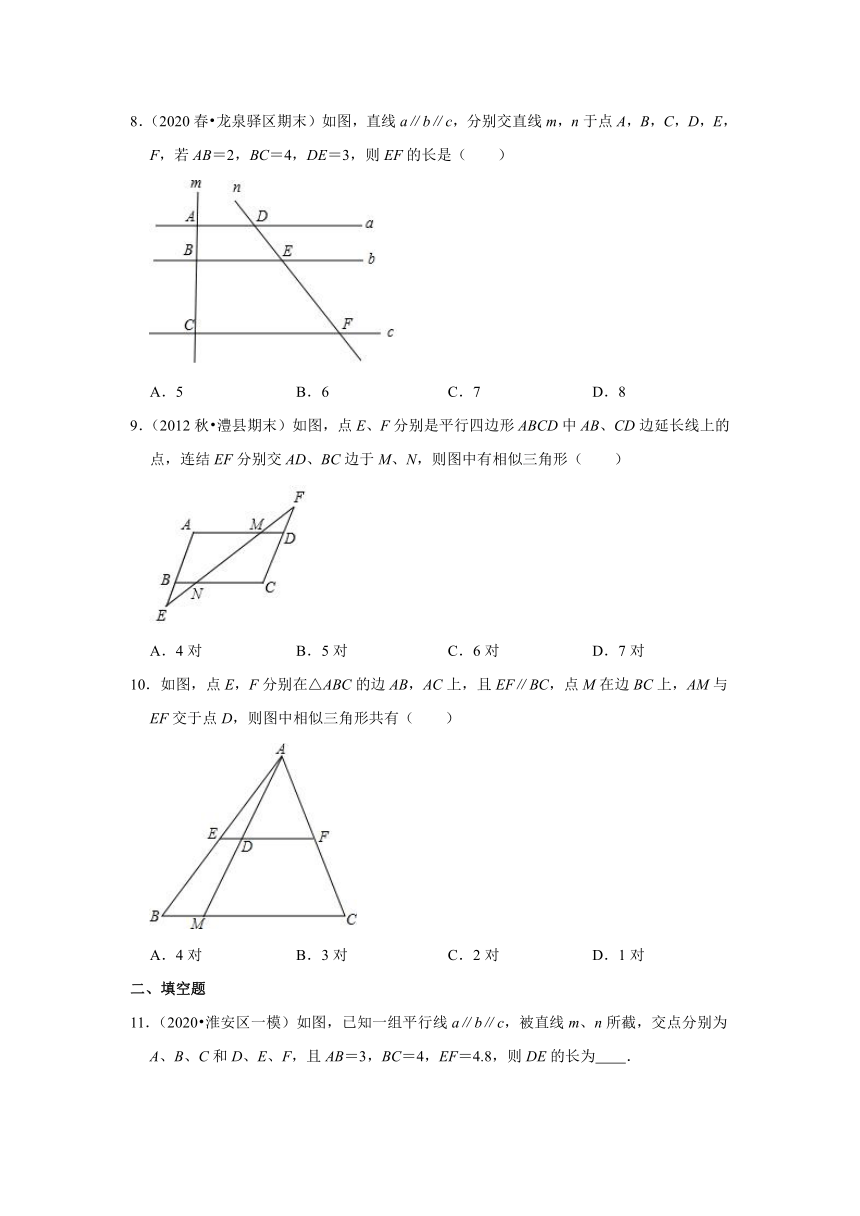
8.(2020春?龙泉驿区期末)如图,直线a∥b∥c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3,则EF的长是( )
A.5 B.6 C.7 D.8
9.(2012秋?澧县期末)如图,点E、F分别是平行四边形ABCD中AB、CD边延长线上的点,连结EF分别交AD、BC边于M、N,则图中有相似三角形( )
A.4对 B.5对 C.6对 D.7对
10.如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
A.4对 B.3对 C.2对 D.1对
二、填空题
11.(2020?淮安区一模)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为 .
12.(2020春?吴中区期末)如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF= .
13.(2020?秦淮区一模)如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
14.(2020?吉林二模)如图,AB∥CD∥EF.若AD:AF=3:5,BC=6,则CE的长为 .
15.(2020?仪征市模拟)如图,已知直线a∥b∥c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=5,BD=3,则BF= .
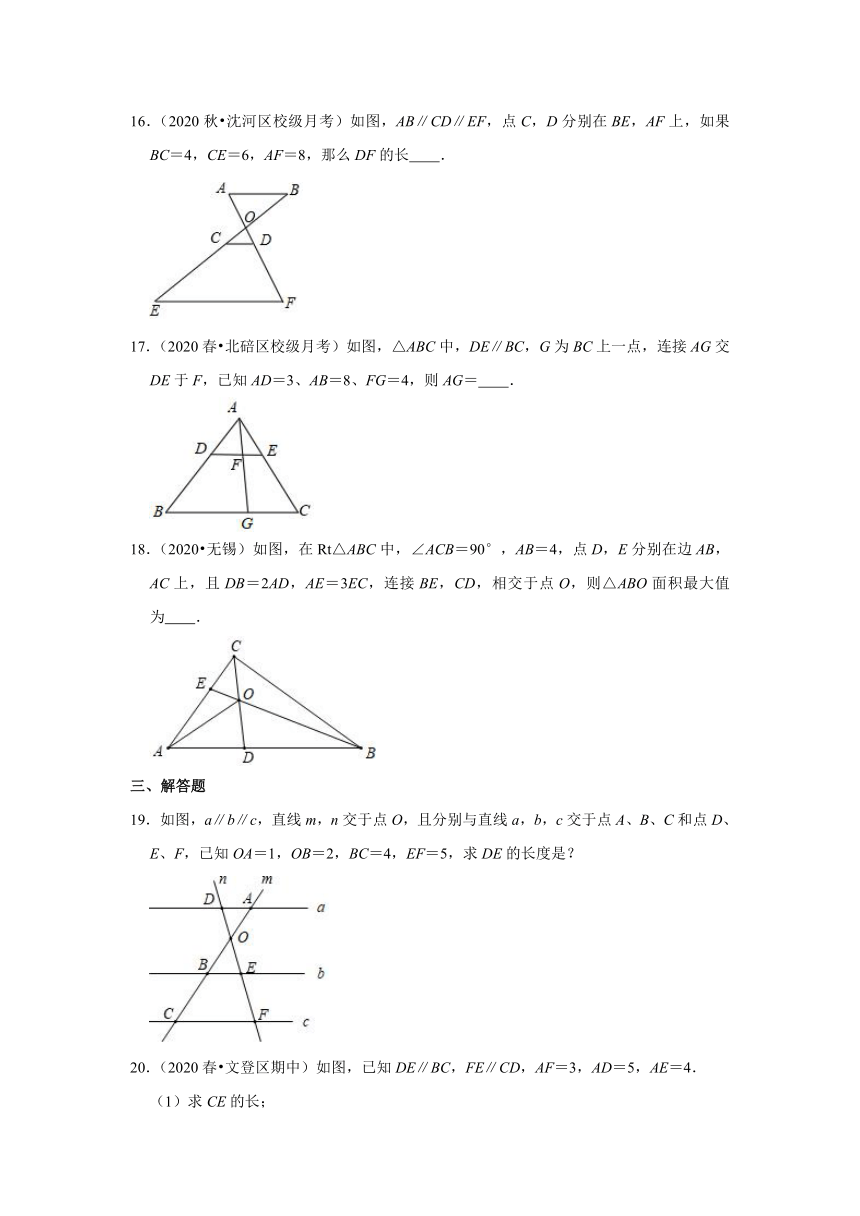
16.(2020秋?沈河区校级月考)如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长 .
17.(2020春?北碚区校级月考)如图,△ABC中,DE∥BC,G为BC上一点,连接AG交DE于F,已知AD=3、AB=8、FG=4,则AG= .
18.(2020?无锡)如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
三、解答题
19.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
20.(2020春?文登区期中)如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
21.如图,OC是∠AOB内的一条射线,点D、D′在OC上,过点D、D′分别作OA、OB的垂线,垂足分别为E、E′和F、F′.
(1)图中有几对相似三角形?是哪几对?
(2)与相等吗?为什么?
22.如图,在△ABC中,点D、E、F分别在BC、AB、AC上,EF∥BC,交AD于点G.
(1)图中有几对相似三角形?是哪几对?
(2)与相等吗?为什么?
23.(2020?浦东新区三模)如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
24.(2019秋?新昌县期末)在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
6.4探索三角形相似的条件(2)
一、选择题
1.(2019秋?宿豫区期末)如图,∠1=∠2,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件不可能是( )
A.∠B=∠D B.∠C=∠E C. D.
2.(2019秋?邳州市期末)如图,在△ABC中,点D、E分别在△ABC的边AB、AC上,不一定能使△ADE与△ABC相似的条件是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
3.(2019秋?常州期末)如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )
A.B.C.D.
4.(2019秋?盐都区期末)如图,△ABC中,点D在边AB上,添加下列条件,不能判定△ACD∽△ABC的是( )
A.∠ACD=∠B B.∠ADC=∠ACB C. D.AC2=AD?AB
5.(2019秋?建湖县期末)如图,在△ABC中,高BD,CE相交于点F,图中与△BEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
6.(2019秋?锡山区期末)如图,在△ABC中,D,E分别是AB,AC的中点,下列说法中不正确的是( )
A.S△ADE:S△ABC=1:2 B.
C.△ADE∽△ABC D.DEBC
7.(2019秋?德州期末)如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③;④AD?BC=DE?AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2 C.3个 D.4个
8.(2019秋?保山期末)如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP?AB;④AB?CP=AP?CB,能满足△APC与△ACB相似的条件是( )
A.①②④ B.①③④ C.②③④ D.①②③
9.(2019秋?灌云县期末)如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,2) B.(6,0) C.(6,3) D.(6,5)
10.(2020?沁阳市二模)平面直角坐标系中,直线yx+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )
A.2 B.3 C.4 D.5
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?海州区校级期末)如图,在△ABC中,P为AB上的一点,补充条件,能使△APC∽△ACB,这个条件可以是 .(写出一个即可)
12.(2019秋?玄武区期末)如图,在△ABC和△APQ中,∠PAB=∠QAC,若再增加一个条件就能使△APQ∽△ABC,则这个条件可以是 .
13.(2020?余干县模拟)如图,△ADE和△ABC中,∠1=∠2,请添加一个适当的条件 ,使△ADE∽△ABC(只填一个即可).
14.(2019秋?工业园区期末)如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA= cm.
15.(2019秋?玄武区期末)如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为点P,则DP= .
16.(2017秋?镇江期末)图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是 .(写出满足条件的所有的点)
17.(2018秋?安庆期中)如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是 .
18.(2020秋?宝应县月考)如图,在△ABC中,AB=6cm,AC=8cm,D是AB上一点且AD=2cm,点E在边AC上,当AE= cm时,使得△ADE与△ABC相似.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?宝应县月考)如图,在正方形ABCD中,点E在AD上,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)连结BF,若△ABE∽△EBF,试确定点E的位置并说明理由.
20.(2020?淮安模拟)如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
21.(2019秋?宿豫区期末)如图,AD、A′D′分别是△ABC和△A′B′C′的中线,且.判断△ABC和△A′B′C′是否相似,并说明理由.
22.(2019秋?临安区期末)如图,点B、D、E在一条直线上,BE交AC于点F,,且∠BAD=∠CAE.
(1)求证:△ABC∽△ADE;
(2)求证:△AEF∽△BCF.
23.(2018秋?霍邱县期末)如图,在△ABC中,AB=3,AC=4,BC=5,D是AB上的一点,AD=2,在线段AC上是否存在一点E,使A,D,E三点组成的三角形与△ABC相似?如果存在,请求出AE的长;如果不存在,请说明理由.
6.4探索三角形相似的条件(1)
一、选择题
1.(2019秋?梁溪区期末)如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.已知AB=1,BC=3,DE=1.2,则DF的长为( )
A.3.6 B.4.8 C.5 D.5.2
【分析】根据平行线分线段成比例定理列出比例式,代入计算得到答案.
【解析】∵AD∥BE∥CF,
∴,即,
解得,EF=3.6,
∴DF=EF+DE=3.6+1.2=4.8,
故选:B.
2.(2019秋?玄武区期末)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=1.5,BC=2,DE=1.8,则EF=( )
A.4.4 B.4 C.3.4 D.2.4
【分析】根据平行线分线段成比例定理列出比例式,代入计算即可.
【解析】∵a∥b∥c,
∴,即,
解得,EF=2.4,
故选:D.
3.(2020春?锡山区期中)如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A. B. C. D.
【分析】根据平行线分线段成比例定理对各个选项进行判断即可.
【解析】∵l1∥l2∥l3,
∴,A错误;
,B错误;
,C错误;
,D正确.
故选:D.
4.(2020秋?惠山区校级月考)如图,l1∥l2∥l3,则下列等式错误的是( )
A. B. C. D.
【分析】如图,观察图形,准确找出图形中的对应线段,正确列出比例式,即可解决问题.
【解析】∵l1∥l2∥l3,
∴,,,,
∴A、B、C都正确,D错误.
故选:D.
5.(2020秋?朝阳区期中)如图,AB∥CD∥EF,AF与BE相交于点G.若AG=2,GD=1,DF=5,BC=4,则BE的长为( )
A. B. C.12 D.20
【分析】利用平行线分线段成比例定理求解.
【解析】∵AB∥CD∥EF,
∴,
∵AD=AG+GD,AG=2,GD=1,DF=5,BC=4,
∴,
∴CE,
∴BE=BC+CE=4;
故选:B.
6.(2020秋?沈阳月考)如图,BE和CD是△ABC的中线,连接DE,则的值是( )
A. B. C. D.
【分析】根据三角形中位线定理和平行线分线段成比例解答即可.
【解析】∵BE和CD是△ABC的中线,
∴DE∥BC,DEBC,
∴,
故选:A.
7.(2020?雨花区校级一模)如图,直线a∥b∥c,则下列结论不正确的为( )
A. B. C. D.
【分析】根据平行线分线段成比例定理定理列出比例式,判断即可.
【解析】A、∵a∥b∥c,
∴,本选项结论正确,不符合题意;
B、∵a∥b∥c,
∴,本选项结论正确,不符合题意;
C、∵a∥b∥c,
∴,本选项结论正确,不符合题意;
D、连接AF,交BE于H,
∵b∥c,
∴△ABH∽△ACF,
∴,本选项结论不正确,符合题意;
故选:D.
8.(2020春?龙泉驿区期末)如图,直线a∥b∥c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3,则EF的长是( )
A.5 B.6 C.7 D.8
【分析】根据平行线分线段成比例定理得到,然后根据比例的性质求EF的长.
【解析】∵直线a∥b∥c,
∴,即,
∴EF=6.
故选:B.
9.(2012秋?澧县期末)如图,点E、F分别是平行四边形ABCD中AB、CD边延长线上的点,连结EF分别交AD、BC边于M、N,则图中有相似三角形( )
A.4对 B.5对 C.6对 D.7对
【分析】由四边形ABCD是平行四边形,可得AD∥BC,AB∥CD,又有相似三角形的判定,即可求得答案.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴图中相似三角形有:△FMD与△FNC,△EBN与△EAM,△EBN与△FCN,△FMD与△EMA,△FMD与△EBN.,△AEM与△NFC.
故选:C.
10.如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
A.4对 B.3对 C.2对 D.1对
【分析】根据相似三角形的判定定理即可得到结论.
【解析】∵EF∥BC,
∴DE∥BM,DF∥CM,
∴△AED∽△ABM,△ADF∽△AMC,△AEF∽△ABC,
∴图中相似三角形共有3对.
故选:B.
二、填空题
11.(2020?淮安区一模)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为 3.6 .
【分析】根据平行线分线段成比例定理列出比例式,代入数据进行计算即可得到答案.
【解析】∵a∥b∥c,
∴,
即,
∴DE=3.6,
故答案为:3.6.
12.(2020春?吴中区期末)如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF= 6 .
【分析】根据平行线分线段成比例定理得出比例式,再代入求出即可.
【解析】∵a∥b∥c,
∴,
∵AB=2,CB=4,DE=3,
∴,
解得:EF=6,
故答案为:6.
13.(2020?秦淮区一模)如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
【分析】过A作DF的平行线,交BE于G,交CF于H,依据BG∥CH,即可得到,进而得出BE的长.
【解析】如图所示,过A作DF的平行线,交BE于G,交CF于H,
则AD=GE=HF=2,CH=6﹣2=4,
∵BG∥CH,
∴,即,
∴BG,
∴BE=BG+GE2,
故答案为:.
14.(2020?吉林二模)如图,AB∥CD∥EF.若AD:AF=3:5,BC=6,则CE的长为 4 .
【分析】三条平行线截两条直线,所得的对应线段成比例.
【解析】∵AB∥CD∥EF,
∴,
∴BE10,
∴CE=BE﹣BC=10﹣6=4,
故答案为4.
15.(2020?仪征市模拟)如图,已知直线a∥b∥c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=5,BD=3,则BF= .
【分析】利用平行线分线段成比例定理得到,这样利用比例性质可求出DF,然后计算BD+DF即可.
【解析】∵a∥b∥c,
∴,即,
∴DF,
∴BF=BD+DF=3.
故答案为.
16.(2020秋?沈河区校级月考)如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长 .
【分析】根据平行线分线段成比例可求解.
【解析】∵AB∥CD∥EF,
∴,
∴,
∴DF,
故答案为:.
17.(2020春?北碚区校级月考)如图,△ABC中,DE∥BC,G为BC上一点,连接AG交DE于F,已知AD=3、AB=8、FG=4,则AG= .
【分析】平行于三角形一边的直线截其他两边,所得的对应线段成比例.依据平行线分线段成比例定理,即可得到AG的长.
【解析】∵DE∥BC,
∴,即,
∴AF,
∴AG=AF+FG4,
故答案为:.
18.(2020?无锡)如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
【分析】过点D作DF∥AE,根据平行线分线段成比例定理可得则,根据已知,可得DO=2OC,C在以AB为直径的圆上,设圆心为G,当CG⊥AB时,△ABC的面积最大为:4×2=4,即可求出此时△ABO的最大面积.
【解析】如图,过点D作DF∥AE,
则,
∵,
∴DF=2EC,
∴DO=2OC,
∴DODC,
∴S△ADOS△ADC,S△BDOS△BDC,
∴S△ABOS△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:4.
故答案为:.
三、解答题
19.(2020春?芝罘区期中)如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
【分析】由平行线分线段成比例定理得出比例式,即可得出结果.
【解析】∵b∥c,
∴,
∴OEEF,
∵a∥c,
∴,
∴DOOF(5),
∴DE=DO+OE.
20.(2020春?文登区期中)如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
【分析】根据平行线分线段成比例定理列出比例式,代入计算即可.
【解析】(1)∵FE∥CD,
∴,即,
解得,AC,
则CE=AC﹣AE4;
(2)∵DE∥BC,
∴,即,
解得,AB.
21.如图,OC是∠AOB内的一条射线,点D、D′在OC上,过点D、D′分别作OA、OB的垂线,垂足分别为E、E′和F、F′.
(1)图中有几对相似三角形?是哪几对?
(2)与相等吗?为什么?
【分析】(1)根据平行线的性质直接判断即可解决问题.
(2)运用相似三角形的性质列出两对比例式,经比较、分析即可解决问题.
【解析】(1)两对;
∵DE⊥OA,D′E′⊥OA,
∴DE∥D′E′,
∴△OD′E′∽△ODE;
同理可证∴△OD′F′∽△ODF.
(2)相等.
∵△OD′E′∽△ODE,
∴,
同理可证,
∴.
22.如图,在△ABC中,点D、E、F分别在BC、AB、AC上,EF∥BC,交AD于点G.
(1)图中有几对相似三角形?是哪几对?
(2)与相等吗?为什么?
【分析】(1)由EF∥BC,可得出△AEF∽△ABC,△AEG∽△ABD,△AGF∽△ADC,此问得解;
(2)由△AEG∽△ABD,利用相似三角形的性质可得出,同理可得出,进而可得出.
【解析】(1)∵EF∥BC,
∴△AEF∽△ABC,△AEG∽△ABD,△AGF∽△ADC,
∴图中有三对相似三角形,分别为:△AEF∽△ABC,△AEG∽△ABD,△AGF∽△ADC.
(2),理由如下:
∵△AEG∽△ABD,
∴.
∵△AGF∽△ADC,
∴,
∴.
23.(2020?浦东新区三模)如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
【分析】(1)根据平行线分线段成比例定理,列出比例式求解即可;
(2)根据平行线分线段成比例定理,列出比例式求解即可.
【解析】(1)∵AD平分∠BAC,∠BAC=60°,
∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=6,
∴CD=2,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,
∴BC=6,
∴BD=BC﹣CD=4,
∵DE∥CA,
∴,
∴DE=4;
(2)如图,
∵点M是线段AD的中点,
∴DM=AM,
∵DE∥CA,
∴,
∴DF=AG,
∵DE∥CA,
∴,
∴,
∵BD=4,BC=6,DF=AG,
∴.
24.(2019秋?新昌县期末)在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
【分析】(1)根据相似三角形的性质可得出结论;
(2)有一个没有进行分类讨论,过点D作∠ADE=∠ACB,则△ADE∽△ACB,可得出结论.
【解答】解(1),
∴.
(2)另一个错在没有进行分类讨论,如图,过点D作∠ADE=∠ACB,
则△ADE∽△ACB,
∴,
∴.
综合以上可得,DE或.
6.4探索三角形相似的条件(2)
一、选择题
1.(2019秋?宿豫区期末)如图,∠1=∠2,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件不可能是( )
A.∠B=∠D B.∠C=∠E C. D.
【分析】根据∠1=∠2可得∠DAE=∠BAC,再结合相似三角形的判定方法进行分析即可.
【解析】∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
∴∠DAE=∠BAC,
A、添加∠B=∠D可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
B、添加∠C=∠E可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
C、添加可利用两边对应成比例且夹角相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
D、添加不能证明△ABC∽△ADE,故此选项符合题意;
故选:D.
2.(2019秋?邳州市期末)如图,在△ABC中,点D、E分别在△ABC的边AB、AC上,不一定能使△ADE与△ABC相似的条件是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
【分析】由已知及三角形相似的判定方法,对每个选项分别分析、判断解答出即可.
【解析】由题意得,∠A=∠A,
A、当∠ADE=∠B时,△ADE∽△ABC;故本选项不符合题意;
B、当∠ADE=∠C时,△ADE∽△ABC;故本选项不符合题意;
C、当时,不能推断△ADE与△ABC相似;故选项符合题意;
D、当时,△ADE∽△ACB;故本选项不符合题意.
故选:C.
3.(2019秋?常州期末)如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )
A. B.
C. D.
【分析】根据AC:BC=2::1,∠ACB=135°,即可判断.
【解析】观察图象可知只有选项C含有135°角,且两边的比为:1,
故选:C.
4.(2019秋?盐都区期末)如图,△ABC中,点D在边AB上,添加下列条件,不能判定△ACD∽△ABC的是( )
A.∠ACD=∠B B.∠ADC=∠ACB C. D.AC2=AD?AB
【分析】根据三角形相似的判定方法一一判断即可.
【解析】A、根据条件可知,由两角对应相等两三角形相似.本选项不符合题意.
B、根据条件可知,由两角对应相等两三角形相似.本选项不符合题意.
C、由条件无法判断两三角形相似.本选项符合题意.
D、根据两边成比例夹角相等两三角形相似,本选项不符合题意,
故选:C.
5.(2019秋?建湖县期末)如图,在△ABC中,高BD,CE相交于点F,图中与△BEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【分析】由三角形的两条高线可得∠BDA=∠BDC=∠CEA=∠CEB=90°、根据∠FBE=∠ABD知△FBE∽△ABD、∠BFE=∠CFD知△BFE∽△CFD、∠FCD=∠ACE知△CFD∽△CAE,从而得△BFE∽△CAE,据此可得答案.
【解析】∵BD⊥AC、CE⊥AB,
∴∠BDA=∠BDC=∠CEA=∠CEB=90°,
∵∠FBE=∠ABD,
∴△FBE∽△ABD,
∵∠BFE=∠CFD,
∴△BFE∽△CFD,
∵∠FCD=∠ACE,
∴△CFD∽△CAE,
∴△BFE∽△CAE,
综上,图中与△BEF相似的三角形有△BAD、△CFD、△CAE这3个,
故选:C.
6.(2019秋?锡山区期末)如图,在△ABC中,D,E分别是AB,AC的中点,下列说法中不正确的是( )
A.S△ADE:S△ABC=1:2 B.
C.△ADE∽△ABC D.DEBC
【分析】由D,E分别是AB,AC的中点,可得出DE是△ABC的中位线,进而可得出DE∥BC,,由DE∥BC可得出△ADE∽△ABC,再利用相似三角形的性质可得出,此题得解.
【解析】∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,,
∴△ADE∽△ABC,DEBC,
∴()2=()2.
故选:A.
7.(2019秋?德州期末)如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③;④AD?BC=DE?AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2 C.3个 D.4个
【分析】根据相似三角形的判定定理对各条件进行逐一判断即可.
【解析】①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;
②DE∥BC,则△ADE∽△ABC,故②不符合题意,
③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;
④由AD?BC=DE?AC可得,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB;
故④不符合题意,
⑤∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故⑤符合题意;
故选:C.
8.(2019秋?保山期末)如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP?AB;④AB?CP=AP?CB,能满足△APC与△ACB相似的条件是( )
A.①②④ B.①③④ C.②③④ D.①②③
【分析】根据有两组角对应相等的两个三角形相似可对①②进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断.
【解析】当∠ACP=∠B,∵∠A=∠A,
所以△APC∽△ACB;
当∠APC=∠ACB,∵∠A=∠A,
所以△APC∽△ACB;
当AC2=AP?AB,
即AC:AB=AP:AC,∵∠A=∠A
所以△APC∽△ACB;
当AB?CP=AP?CB,即PC:BC=AP:AB,
而∠PAC=∠CAB,
所以不能判断△APC和△ACB相似.
故选:D.
9.(2019秋?灌云县期末)如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,2) B.(6,0) C.(6,3) D.(6,5)
【分析】利用A、B、C的坐标得到AB=6,BC=3,∠ABC=90°,然后利用两组对应边的比相等且夹角对应相等的两个三角形相似对各选项进行判断.
【解析】∵点A、B、C的坐标分别是(1,7),(1,1),(4,1),
∴AB=6,BC=3,∠ABC=90°,
当E点坐标为(4,2),而D(6,1),则CE=1,CD=2,∠ECD=90°,
∵3,∠ABC=∠ECD,
∴△ABC∽△DCE;
当E点坐标为(6,0),而D(6,1),则ED=1,CD=2,∠EDC=90°,
∵3,∠ABC=∠EDC,
∴△ABC∽△EDC;
当E点坐标为(6,3),而D(6,1),则ED=2,CD=2,∠EDC=90°,
∵,∠ABC=∠EDC,
∴△ABC与△ECD不相似;
当E点坐标为(6,5),而D(6,1),则ED=4,CD=2,∠EDC=90°,
∵,∠ABC=∠EDC,
∴△ABC∽△EDC.
故选:C.
10.(2020?沁阳市二模)平面直角坐标系中,直线yx+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )
A.2 B.3 C.4 D.5
【分析】根据相似三角形的相似条件,画出图形即可解决问题.
【解析】如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?海州区校级期末)如图,在△ABC中,P为AB上的一点,补充条件,能使△APC∽△ACB,这个条件可以是 ∠ACP=∠B(答案不唯一) .(写出一个即可)
【分析】△APC和△ACB有公共角∠A,则根据有两组角对应相等的两个三角形相似解答即可.
【解析】∵∠PAC=∠CAB,
∴当∠ACP=∠B时,△ACP∽△APC,
故答案为:∠ACP=∠B(答案不唯一)
12.(2019秋?玄武区期末)如图,在△ABC和△APQ中,∠PAB=∠QAC,若再增加一个条件就能使△APQ∽△ABC,则这个条件可以是 ∠P=∠B或∠Q=∠C或 .
【分析】由∠PAB=∠QAC,可得∠PAQ=∠BAC,要使△APQ∽△ABC,可根据相似三角形的判定,添加恰当条件.
【解析】∵∠PAB=∠QAC,
∴∠PAQ=∠BAC,
若∠P=∠B,则△APQ∽△ABC,
若∠Q=∠C,则△APQ∽△ABC,
若,则△APQ∽△ABC,
故答案为:∠P=∠B或∠Q=∠C或.
13.(2020?余干县模拟)如图,△ADE和△ABC中,∠1=∠2,请添加一个适当的条件 ∠D=∠B或∠E=∠C或 ,使△ADE∽△ABC(只填一个即可).
【分析】根据相似三角形的判定方法,已知一组角相等则再添加一组相等的角或夹该角的两边对应成比例即可推出两三角形相似.
【解析】∵∠1=∠2,
∴∠DAE=∠BAC,
∴要使△ADE∽△ABC,则添加的一个条件可以是∠D=∠B或∠E=∠C或.
故答案为:∠D=∠B或∠E=∠C或.
14.(2019秋?工业园区期末)如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA= 2或3 cm.
【分析】根据相似三角形的判定与性质,当若点A,P,D分别与点B,C,P对应,与若点A,P,D分别与点B,P,C对应,分别分析得出AP的长度即可.
【解析】设AP=xcm.则BP=AB﹣AP=(5﹣x)cm
以A,D,P为顶点的三角形与以B,C,P为顶点的三角形相似,
①当AD:PB=PA:BC时,
,
解得x=2或3.
②当AD:BC=PA:PB时,,解得x=3,
∴当A,D,P为顶点的三角形与以B,C,P为顶点的三角形相似,AP的值为2或3.
故答案为2或3.
15.(2019秋?玄武区期末)如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为点P,则DP= 1或或 .
【分析】分三种情况讨论,由相似三角形的性质可求解.
【解析】如图1,若DP∥AB,
∴△CDP∽△CBA,
∴,
∴
∴DP=1;
如图2,若DP∥AC,
∴△BDP∽△BCA,
∴,
∴
∴PD;
如图3,若∠CPD=∠B,且∠C=∠C,
∴△CDP∽△CAB,
∴,
∴,
∴PD,
故答案为:1或或.
16.(2017秋?镇江期末)图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是 Q或G .(写出满足条件的所有的点)
【分析】这个点是点Q或G,根据两边成比例夹角相等即可判断.
【解析】这个点是点Q.
∵∠ABC=∠QDE,,,
∴,
∴△ABC∽QDE,
同法可得:,△ABC∽△EDG,
故答案为Q或G.
17.(2018秋?安庆期中)如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是 秒或秒 .
【分析】如果以点A、D、E为顶点的三角形与△ABC相似,由于A与A对应,那么分两种情况:①D与B对应;②D与C对应.根据相似三角形的性质分别作答.
【解析】如果两点同时运动,设运动t秒时,以点A、D、E为顶点的三角形与△ABC相似,
则AD=t,CE=2t,AE=AC﹣CE=6﹣2t.
①当D与B对应时,有△ADE∽△ABC.
∴AD:AB=AE:AC,
∴t:3=(6﹣2t):6,
∴t;
②当D与C对应时,有△ADE∽△ACB.
∴AD:AC=AE:AB,
∴t:6=(6﹣2t):3,
∴t.
∴当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是秒或秒.
故答案为:秒或秒.
18.(2020秋?宝应县月考)如图,在△ABC中,AB=6cm,AC=8cm,D是AB上一点且AD=2cm,点E在边AC上,当AE= 或1.5 cm时,使得△ADE与△ABC相似.
【分析】分两种情形利用相似三角形的性质求解即可.
【解析】有两种情形:
如图,当DE∥BC时,△ADE∽△ABC,
∴,
∴,
∴AE(cm),
当∠ADE′=∠C时,∵∠A=∠A,
∴△ADE′∽△ACB,
∴,
∴,
∴AE′=1.5(cm),
故答案为或1.5.
三、解答题
19.(2020秋?宝应县月考)如图,在正方形ABCD中,点E在AD上,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)连结BF,若△ABE∽△EBF,试确定点E的位置并说明理由.
【分析】(1)利用“两角法”证得△ABE∽△DEF;
(2)根据相似三角形的对应边成比例解答.
【解答】(1)证明∵四边形ABCD是正方形,
∴∠A=∠D=90°.
∴∠AEB+∠ABE=90°.
∵EF⊥BE,
∴∠AEB+∠DEF=90°.
∴∠ABE=∠DEF.
在△ABE和△DEF中,∠ABE=∠DEF,∠A=∠D,
∴△ABE∽△DEF;
(2)∵△ABE∽△DEF,
∴.
∵△ABE∽△EBF,
∴.
∴.
∴DE=AE.
∴点E为AD的中点.
20.(2020?淮安模拟)如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
【分析】(1)先利用等腰三角形的性质得出∠B=∠C,再由∠BDE=∠CAD可证得△BDE∽△CAD;
(2)先由(1)中相似三角形的性质得∠BED=∠ADC,再利用等角的补角相等,证得∠AED=∠ADB,然后结合两个三角形有一个公共角可证得结论.
【解析】(1)证明:∵AB=AC,
∴∠B=∠C,
又∵∠BDE=∠CAD,
∴△BDE∽△CAD;
(2)证明:∵△BDE∽△CAD,
∴∠BED=∠CDA,
∴180°﹣∠BED=180°﹣∠CDA
即∠AED=∠ADB.
又∵∠BAD=∠DAE,
∴△ADE∽△ABD.
21.(2019秋?宿豫区期末)如图,AD、A′D′分别是△ABC和△A′B′C′的中线,且.判断△ABC和△A′B′C′是否相似,并说明理由.
【分析】根据相似三角形的判定解答即可.
【解析】△ABC∽△A'B'C',
理由:∵
∴△ABD∽△A'B'D',
∴∠B=∠B',
∵AD、A'D'分别是△ABC和△A'B'C'的中线
∴,,
∴,
在△ABC和△A'B'C'中
∵,且∠B=∠B'
∴△ABC∽△A'B'C'.
22.(2019秋?临安区期末)如图,点B、D、E在一条直线上,BE交AC于点F,,且∠BAD=∠CAE.
(1)求证:△ABC∽△ADE;
(2)求证:△AEF∽△BCF.
【分析】(1)根据相似三角形的判定定理证明;
(2)根据相似三角形的性质定理得到∠C=∠E,结合图形,证明即可.
【解答】(1)∵∠BAD=∠CAE
∴∠BAD+∠CAD=∠CAE+∠CAD
即∠BAC=∠DAE
在△ABC和△ADE中
,∠BAC=∠DAE,
∴△ABC∽△ADE;
(2)∵△ABC∽△ADE,
∴∠C=∠E、
在△AEF和△BFC中,∠C=∠E,∠AFE=∠BFC,
∴△AEF∽△BCF.
23.(2018秋?霍邱县期末)如图,在△ABC中,AB=3,AC=4,BC=5,D是AB上的一点,AD=2,在线段AC上是否存在一点E,使A,D,E三点组成的三角形与△ABC相似?如果存在,请求出AE的长;如果不存在,请说明理由.
【分析】由勾股定理的逆定理可得∠BAC=90°,由相似三角形的性质可求解.
【解析】存在,
∵AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∵A,D,E三点组成的三角形与△ABC相似,
∴△ABC∽△ADE或△ABC∽△AED,
∴或,
∴,
∴AE或,
一、选择题
1.(2019秋?梁溪区期末)如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.已知AB=1,BC=3,DE=1.2,则DF的长为( )
A.3.6 B.4.8 C.5 D.5.2
2.(2019秋?玄武区期末)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=1.5,BC=2,DE=1.8,则EF=( )
A.4.4 B.4 C.3.4 D.2.4
3.(2020春?锡山区期中)如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A. B. C. D.
4.(2020秋?惠山区校级月考)如图,l1∥l2∥l3,则下列等式错误的是( )
A. B. C. D.
5.(2020秋?朝阳区期中)如图,AB∥CD∥EF,AF与BE相交于点G.若AG=2,GD=1,DF=5,BC=4,则BE的长为( )
A. B. C.12 D.20
6.(2020秋?沈阳月考)如图,BE和CD是△ABC的中线,连接DE,则的值是( )
A. B. C. D.
7.(2020?雨花区校级一模)如图,直线a∥b∥c,则下列结论不正确的为( )
A. B. C. D.
8.(2020春?龙泉驿区期末)如图,直线a∥b∥c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3,则EF的长是( )
A.5 B.6 C.7 D.8
9.(2012秋?澧县期末)如图,点E、F分别是平行四边形ABCD中AB、CD边延长线上的点,连结EF分别交AD、BC边于M、N,则图中有相似三角形( )
A.4对 B.5对 C.6对 D.7对
10.如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
A.4对 B.3对 C.2对 D.1对
二、填空题
11.(2020?淮安区一模)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为 .
12.(2020春?吴中区期末)如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF= .
13.(2020?秦淮区一模)如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
14.(2020?吉林二模)如图,AB∥CD∥EF.若AD:AF=3:5,BC=6,则CE的长为 .
15.(2020?仪征市模拟)如图,已知直线a∥b∥c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=5,BD=3,则BF= .
16.(2020秋?沈河区校级月考)如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长 .
17.(2020春?北碚区校级月考)如图,△ABC中,DE∥BC,G为BC上一点,连接AG交DE于F,已知AD=3、AB=8、FG=4,则AG= .
18.(2020?无锡)如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
三、解答题
19.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
20.(2020春?文登区期中)如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
21.如图,OC是∠AOB内的一条射线,点D、D′在OC上,过点D、D′分别作OA、OB的垂线,垂足分别为E、E′和F、F′.
(1)图中有几对相似三角形?是哪几对?
(2)与相等吗?为什么?
22.如图,在△ABC中,点D、E、F分别在BC、AB、AC上,EF∥BC,交AD于点G.
(1)图中有几对相似三角形?是哪几对?
(2)与相等吗?为什么?
23.(2020?浦东新区三模)如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
24.(2019秋?新昌县期末)在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
6.4探索三角形相似的条件(2)
一、选择题
1.(2019秋?宿豫区期末)如图,∠1=∠2,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件不可能是( )
A.∠B=∠D B.∠C=∠E C. D.
2.(2019秋?邳州市期末)如图,在△ABC中,点D、E分别在△ABC的边AB、AC上,不一定能使△ADE与△ABC相似的条件是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
3.(2019秋?常州期末)如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )
A.B.C.D.
4.(2019秋?盐都区期末)如图,△ABC中,点D在边AB上,添加下列条件,不能判定△ACD∽△ABC的是( )
A.∠ACD=∠B B.∠ADC=∠ACB C. D.AC2=AD?AB
5.(2019秋?建湖县期末)如图,在△ABC中,高BD,CE相交于点F,图中与△BEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
6.(2019秋?锡山区期末)如图,在△ABC中,D,E分别是AB,AC的中点,下列说法中不正确的是( )
A.S△ADE:S△ABC=1:2 B.
C.△ADE∽△ABC D.DEBC
7.(2019秋?德州期末)如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③;④AD?BC=DE?AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2 C.3个 D.4个
8.(2019秋?保山期末)如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP?AB;④AB?CP=AP?CB,能满足△APC与△ACB相似的条件是( )
A.①②④ B.①③④ C.②③④ D.①②③
9.(2019秋?灌云县期末)如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,2) B.(6,0) C.(6,3) D.(6,5)
10.(2020?沁阳市二模)平面直角坐标系中,直线yx+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )
A.2 B.3 C.4 D.5
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?海州区校级期末)如图,在△ABC中,P为AB上的一点,补充条件,能使△APC∽△ACB,这个条件可以是 .(写出一个即可)
12.(2019秋?玄武区期末)如图,在△ABC和△APQ中,∠PAB=∠QAC,若再增加一个条件就能使△APQ∽△ABC,则这个条件可以是 .
13.(2020?余干县模拟)如图,△ADE和△ABC中,∠1=∠2,请添加一个适当的条件 ,使△ADE∽△ABC(只填一个即可).
14.(2019秋?工业园区期末)如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA= cm.
15.(2019秋?玄武区期末)如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为点P,则DP= .
16.(2017秋?镇江期末)图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是 .(写出满足条件的所有的点)
17.(2018秋?安庆期中)如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是 .
18.(2020秋?宝应县月考)如图,在△ABC中,AB=6cm,AC=8cm,D是AB上一点且AD=2cm,点E在边AC上,当AE= cm时,使得△ADE与△ABC相似.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?宝应县月考)如图,在正方形ABCD中,点E在AD上,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)连结BF,若△ABE∽△EBF,试确定点E的位置并说明理由.
20.(2020?淮安模拟)如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
21.(2019秋?宿豫区期末)如图,AD、A′D′分别是△ABC和△A′B′C′的中线,且.判断△ABC和△A′B′C′是否相似,并说明理由.
22.(2019秋?临安区期末)如图,点B、D、E在一条直线上,BE交AC于点F,,且∠BAD=∠CAE.
(1)求证:△ABC∽△ADE;
(2)求证:△AEF∽△BCF.
23.(2018秋?霍邱县期末)如图,在△ABC中,AB=3,AC=4,BC=5,D是AB上的一点,AD=2,在线段AC上是否存在一点E,使A,D,E三点组成的三角形与△ABC相似?如果存在,请求出AE的长;如果不存在,请说明理由.
6.4探索三角形相似的条件(1)
一、选择题
1.(2019秋?梁溪区期末)如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.已知AB=1,BC=3,DE=1.2,则DF的长为( )
A.3.6 B.4.8 C.5 D.5.2
【分析】根据平行线分线段成比例定理列出比例式,代入计算得到答案.
【解析】∵AD∥BE∥CF,
∴,即,
解得,EF=3.6,
∴DF=EF+DE=3.6+1.2=4.8,
故选:B.
2.(2019秋?玄武区期末)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=1.5,BC=2,DE=1.8,则EF=( )
A.4.4 B.4 C.3.4 D.2.4
【分析】根据平行线分线段成比例定理列出比例式,代入计算即可.
【解析】∵a∥b∥c,
∴,即,
解得,EF=2.4,
故选:D.
3.(2020春?锡山区期中)如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A. B. C. D.
【分析】根据平行线分线段成比例定理对各个选项进行判断即可.
【解析】∵l1∥l2∥l3,
∴,A错误;
,B错误;
,C错误;
,D正确.
故选:D.
4.(2020秋?惠山区校级月考)如图,l1∥l2∥l3,则下列等式错误的是( )
A. B. C. D.
【分析】如图,观察图形,准确找出图形中的对应线段,正确列出比例式,即可解决问题.
【解析】∵l1∥l2∥l3,
∴,,,,
∴A、B、C都正确,D错误.
故选:D.
5.(2020秋?朝阳区期中)如图,AB∥CD∥EF,AF与BE相交于点G.若AG=2,GD=1,DF=5,BC=4,则BE的长为( )
A. B. C.12 D.20
【分析】利用平行线分线段成比例定理求解.
【解析】∵AB∥CD∥EF,
∴,
∵AD=AG+GD,AG=2,GD=1,DF=5,BC=4,
∴,
∴CE,
∴BE=BC+CE=4;
故选:B.
6.(2020秋?沈阳月考)如图,BE和CD是△ABC的中线,连接DE,则的值是( )
A. B. C. D.
【分析】根据三角形中位线定理和平行线分线段成比例解答即可.
【解析】∵BE和CD是△ABC的中线,
∴DE∥BC,DEBC,
∴,
故选:A.
7.(2020?雨花区校级一模)如图,直线a∥b∥c,则下列结论不正确的为( )
A. B. C. D.
【分析】根据平行线分线段成比例定理定理列出比例式,判断即可.
【解析】A、∵a∥b∥c,
∴,本选项结论正确,不符合题意;
B、∵a∥b∥c,
∴,本选项结论正确,不符合题意;
C、∵a∥b∥c,
∴,本选项结论正确,不符合题意;
D、连接AF,交BE于H,
∵b∥c,
∴△ABH∽△ACF,
∴,本选项结论不正确,符合题意;
故选:D.
8.(2020春?龙泉驿区期末)如图,直线a∥b∥c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3,则EF的长是( )
A.5 B.6 C.7 D.8
【分析】根据平行线分线段成比例定理得到,然后根据比例的性质求EF的长.
【解析】∵直线a∥b∥c,
∴,即,
∴EF=6.
故选:B.
9.(2012秋?澧县期末)如图,点E、F分别是平行四边形ABCD中AB、CD边延长线上的点,连结EF分别交AD、BC边于M、N,则图中有相似三角形( )
A.4对 B.5对 C.6对 D.7对
【分析】由四边形ABCD是平行四边形,可得AD∥BC,AB∥CD,又有相似三角形的判定,即可求得答案.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴图中相似三角形有:△FMD与△FNC,△EBN与△EAM,△EBN与△FCN,△FMD与△EMA,△FMD与△EBN.,△AEM与△NFC.
故选:C.
10.如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
A.4对 B.3对 C.2对 D.1对
【分析】根据相似三角形的判定定理即可得到结论.
【解析】∵EF∥BC,
∴DE∥BM,DF∥CM,
∴△AED∽△ABM,△ADF∽△AMC,△AEF∽△ABC,
∴图中相似三角形共有3对.
故选:B.
二、填空题
11.(2020?淮安区一模)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为 3.6 .
【分析】根据平行线分线段成比例定理列出比例式,代入数据进行计算即可得到答案.
【解析】∵a∥b∥c,
∴,
即,
∴DE=3.6,
故答案为:3.6.
12.(2020春?吴中区期末)如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF= 6 .
【分析】根据平行线分线段成比例定理得出比例式,再代入求出即可.
【解析】∵a∥b∥c,
∴,
∵AB=2,CB=4,DE=3,
∴,
解得:EF=6,
故答案为:6.
13.(2020?秦淮区一模)如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
【分析】过A作DF的平行线,交BE于G,交CF于H,依据BG∥CH,即可得到,进而得出BE的长.
【解析】如图所示,过A作DF的平行线,交BE于G,交CF于H,
则AD=GE=HF=2,CH=6﹣2=4,
∵BG∥CH,
∴,即,
∴BG,
∴BE=BG+GE2,
故答案为:.
14.(2020?吉林二模)如图,AB∥CD∥EF.若AD:AF=3:5,BC=6,则CE的长为 4 .
【分析】三条平行线截两条直线,所得的对应线段成比例.
【解析】∵AB∥CD∥EF,
∴,
∴BE10,
∴CE=BE﹣BC=10﹣6=4,
故答案为4.
15.(2020?仪征市模拟)如图,已知直线a∥b∥c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=5,BD=3,则BF= .
【分析】利用平行线分线段成比例定理得到,这样利用比例性质可求出DF,然后计算BD+DF即可.
【解析】∵a∥b∥c,
∴,即,
∴DF,
∴BF=BD+DF=3.
故答案为.
16.(2020秋?沈河区校级月考)如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长 .
【分析】根据平行线分线段成比例可求解.
【解析】∵AB∥CD∥EF,
∴,
∴,
∴DF,
故答案为:.
17.(2020春?北碚区校级月考)如图,△ABC中,DE∥BC,G为BC上一点,连接AG交DE于F,已知AD=3、AB=8、FG=4,则AG= .
【分析】平行于三角形一边的直线截其他两边,所得的对应线段成比例.依据平行线分线段成比例定理,即可得到AG的长.
【解析】∵DE∥BC,
∴,即,
∴AF,
∴AG=AF+FG4,
故答案为:.
18.(2020?无锡)如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
【分析】过点D作DF∥AE,根据平行线分线段成比例定理可得则,根据已知,可得DO=2OC,C在以AB为直径的圆上,设圆心为G,当CG⊥AB时,△ABC的面积最大为:4×2=4,即可求出此时△ABO的最大面积.
【解析】如图,过点D作DF∥AE,
则,
∵,
∴DF=2EC,
∴DO=2OC,
∴DODC,
∴S△ADOS△ADC,S△BDOS△BDC,
∴S△ABOS△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:4.
故答案为:.
三、解答题
19.(2020春?芝罘区期中)如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
【分析】由平行线分线段成比例定理得出比例式,即可得出结果.
【解析】∵b∥c,
∴,
∴OEEF,
∵a∥c,
∴,
∴DOOF(5),
∴DE=DO+OE.
20.(2020春?文登区期中)如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
【分析】根据平行线分线段成比例定理列出比例式,代入计算即可.
【解析】(1)∵FE∥CD,
∴,即,
解得,AC,
则CE=AC﹣AE4;
(2)∵DE∥BC,
∴,即,
解得,AB.
21.如图,OC是∠AOB内的一条射线,点D、D′在OC上,过点D、D′分别作OA、OB的垂线,垂足分别为E、E′和F、F′.
(1)图中有几对相似三角形?是哪几对?
(2)与相等吗?为什么?
【分析】(1)根据平行线的性质直接判断即可解决问题.
(2)运用相似三角形的性质列出两对比例式,经比较、分析即可解决问题.
【解析】(1)两对;
∵DE⊥OA,D′E′⊥OA,
∴DE∥D′E′,
∴△OD′E′∽△ODE;
同理可证∴△OD′F′∽△ODF.
(2)相等.
∵△OD′E′∽△ODE,
∴,
同理可证,
∴.
22.如图,在△ABC中,点D、E、F分别在BC、AB、AC上,EF∥BC,交AD于点G.
(1)图中有几对相似三角形?是哪几对?
(2)与相等吗?为什么?
【分析】(1)由EF∥BC,可得出△AEF∽△ABC,△AEG∽△ABD,△AGF∽△ADC,此问得解;
(2)由△AEG∽△ABD,利用相似三角形的性质可得出,同理可得出,进而可得出.
【解析】(1)∵EF∥BC,
∴△AEF∽△ABC,△AEG∽△ABD,△AGF∽△ADC,
∴图中有三对相似三角形,分别为:△AEF∽△ABC,△AEG∽△ABD,△AGF∽△ADC.
(2),理由如下:
∵△AEG∽△ABD,
∴.
∵△AGF∽△ADC,
∴,
∴.
23.(2020?浦东新区三模)如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
【分析】(1)根据平行线分线段成比例定理,列出比例式求解即可;
(2)根据平行线分线段成比例定理,列出比例式求解即可.
【解析】(1)∵AD平分∠BAC,∠BAC=60°,
∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=6,
∴CD=2,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,
∴BC=6,
∴BD=BC﹣CD=4,
∵DE∥CA,
∴,
∴DE=4;
(2)如图,
∵点M是线段AD的中点,
∴DM=AM,
∵DE∥CA,
∴,
∴DF=AG,
∵DE∥CA,
∴,
∴,
∵BD=4,BC=6,DF=AG,
∴.
24.(2019秋?新昌县期末)在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
【分析】(1)根据相似三角形的性质可得出结论;
(2)有一个没有进行分类讨论,过点D作∠ADE=∠ACB,则△ADE∽△ACB,可得出结论.
【解答】解(1),
∴.
(2)另一个错在没有进行分类讨论,如图,过点D作∠ADE=∠ACB,
则△ADE∽△ACB,
∴,
∴.
综合以上可得,DE或.
6.4探索三角形相似的条件(2)
一、选择题
1.(2019秋?宿豫区期末)如图,∠1=∠2,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件不可能是( )
A.∠B=∠D B.∠C=∠E C. D.
【分析】根据∠1=∠2可得∠DAE=∠BAC,再结合相似三角形的判定方法进行分析即可.
【解析】∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
∴∠DAE=∠BAC,
A、添加∠B=∠D可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
B、添加∠C=∠E可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
C、添加可利用两边对应成比例且夹角相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
D、添加不能证明△ABC∽△ADE,故此选项符合题意;
故选:D.
2.(2019秋?邳州市期末)如图,在△ABC中,点D、E分别在△ABC的边AB、AC上,不一定能使△ADE与△ABC相似的条件是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
【分析】由已知及三角形相似的判定方法,对每个选项分别分析、判断解答出即可.
【解析】由题意得,∠A=∠A,
A、当∠ADE=∠B时,△ADE∽△ABC;故本选项不符合题意;
B、当∠ADE=∠C时,△ADE∽△ABC;故本选项不符合题意;
C、当时,不能推断△ADE与△ABC相似;故选项符合题意;
D、当时,△ADE∽△ACB;故本选项不符合题意.
故选:C.
3.(2019秋?常州期末)如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )
A. B.
C. D.
【分析】根据AC:BC=2::1,∠ACB=135°,即可判断.
【解析】观察图象可知只有选项C含有135°角,且两边的比为:1,
故选:C.
4.(2019秋?盐都区期末)如图,△ABC中,点D在边AB上,添加下列条件,不能判定△ACD∽△ABC的是( )
A.∠ACD=∠B B.∠ADC=∠ACB C. D.AC2=AD?AB
【分析】根据三角形相似的判定方法一一判断即可.
【解析】A、根据条件可知,由两角对应相等两三角形相似.本选项不符合题意.
B、根据条件可知,由两角对应相等两三角形相似.本选项不符合题意.
C、由条件无法判断两三角形相似.本选项符合题意.
D、根据两边成比例夹角相等两三角形相似,本选项不符合题意,
故选:C.
5.(2019秋?建湖县期末)如图,在△ABC中,高BD,CE相交于点F,图中与△BEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【分析】由三角形的两条高线可得∠BDA=∠BDC=∠CEA=∠CEB=90°、根据∠FBE=∠ABD知△FBE∽△ABD、∠BFE=∠CFD知△BFE∽△CFD、∠FCD=∠ACE知△CFD∽△CAE,从而得△BFE∽△CAE,据此可得答案.
【解析】∵BD⊥AC、CE⊥AB,
∴∠BDA=∠BDC=∠CEA=∠CEB=90°,
∵∠FBE=∠ABD,
∴△FBE∽△ABD,
∵∠BFE=∠CFD,
∴△BFE∽△CFD,
∵∠FCD=∠ACE,
∴△CFD∽△CAE,
∴△BFE∽△CAE,
综上,图中与△BEF相似的三角形有△BAD、△CFD、△CAE这3个,
故选:C.
6.(2019秋?锡山区期末)如图,在△ABC中,D,E分别是AB,AC的中点,下列说法中不正确的是( )
A.S△ADE:S△ABC=1:2 B.
C.△ADE∽△ABC D.DEBC
【分析】由D,E分别是AB,AC的中点,可得出DE是△ABC的中位线,进而可得出DE∥BC,,由DE∥BC可得出△ADE∽△ABC,再利用相似三角形的性质可得出,此题得解.
【解析】∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,,
∴△ADE∽△ABC,DEBC,
∴()2=()2.
故选:A.
7.(2019秋?德州期末)如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③;④AD?BC=DE?AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2 C.3个 D.4个
【分析】根据相似三角形的判定定理对各条件进行逐一判断即可.
【解析】①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;
②DE∥BC,则△ADE∽△ABC,故②不符合题意,
③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;
④由AD?BC=DE?AC可得,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB;
故④不符合题意,
⑤∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故⑤符合题意;
故选:C.
8.(2019秋?保山期末)如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP?AB;④AB?CP=AP?CB,能满足△APC与△ACB相似的条件是( )
A.①②④ B.①③④ C.②③④ D.①②③
【分析】根据有两组角对应相等的两个三角形相似可对①②进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断.
【解析】当∠ACP=∠B,∵∠A=∠A,
所以△APC∽△ACB;
当∠APC=∠ACB,∵∠A=∠A,
所以△APC∽△ACB;
当AC2=AP?AB,
即AC:AB=AP:AC,∵∠A=∠A
所以△APC∽△ACB;
当AB?CP=AP?CB,即PC:BC=AP:AB,
而∠PAC=∠CAB,
所以不能判断△APC和△ACB相似.
故选:D.
9.(2019秋?灌云县期末)如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,2) B.(6,0) C.(6,3) D.(6,5)
【分析】利用A、B、C的坐标得到AB=6,BC=3,∠ABC=90°,然后利用两组对应边的比相等且夹角对应相等的两个三角形相似对各选项进行判断.
【解析】∵点A、B、C的坐标分别是(1,7),(1,1),(4,1),
∴AB=6,BC=3,∠ABC=90°,
当E点坐标为(4,2),而D(6,1),则CE=1,CD=2,∠ECD=90°,
∵3,∠ABC=∠ECD,
∴△ABC∽△DCE;
当E点坐标为(6,0),而D(6,1),则ED=1,CD=2,∠EDC=90°,
∵3,∠ABC=∠EDC,
∴△ABC∽△EDC;
当E点坐标为(6,3),而D(6,1),则ED=2,CD=2,∠EDC=90°,
∵,∠ABC=∠EDC,
∴△ABC与△ECD不相似;
当E点坐标为(6,5),而D(6,1),则ED=4,CD=2,∠EDC=90°,
∵,∠ABC=∠EDC,
∴△ABC∽△EDC.
故选:C.
10.(2020?沁阳市二模)平面直角坐标系中,直线yx+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )
A.2 B.3 C.4 D.5
【分析】根据相似三角形的相似条件,画出图形即可解决问题.
【解析】如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?海州区校级期末)如图,在△ABC中,P为AB上的一点,补充条件,能使△APC∽△ACB,这个条件可以是 ∠ACP=∠B(答案不唯一) .(写出一个即可)
【分析】△APC和△ACB有公共角∠A,则根据有两组角对应相等的两个三角形相似解答即可.
【解析】∵∠PAC=∠CAB,
∴当∠ACP=∠B时,△ACP∽△APC,
故答案为:∠ACP=∠B(答案不唯一)
12.(2019秋?玄武区期末)如图,在△ABC和△APQ中,∠PAB=∠QAC,若再增加一个条件就能使△APQ∽△ABC,则这个条件可以是 ∠P=∠B或∠Q=∠C或 .
【分析】由∠PAB=∠QAC,可得∠PAQ=∠BAC,要使△APQ∽△ABC,可根据相似三角形的判定,添加恰当条件.
【解析】∵∠PAB=∠QAC,
∴∠PAQ=∠BAC,
若∠P=∠B,则△APQ∽△ABC,
若∠Q=∠C,则△APQ∽△ABC,
若,则△APQ∽△ABC,
故答案为:∠P=∠B或∠Q=∠C或.
13.(2020?余干县模拟)如图,△ADE和△ABC中,∠1=∠2,请添加一个适当的条件 ∠D=∠B或∠E=∠C或 ,使△ADE∽△ABC(只填一个即可).
【分析】根据相似三角形的判定方法,已知一组角相等则再添加一组相等的角或夹该角的两边对应成比例即可推出两三角形相似.
【解析】∵∠1=∠2,
∴∠DAE=∠BAC,
∴要使△ADE∽△ABC,则添加的一个条件可以是∠D=∠B或∠E=∠C或.
故答案为:∠D=∠B或∠E=∠C或.
14.(2019秋?工业园区期末)如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA= 2或3 cm.
【分析】根据相似三角形的判定与性质,当若点A,P,D分别与点B,C,P对应,与若点A,P,D分别与点B,P,C对应,分别分析得出AP的长度即可.
【解析】设AP=xcm.则BP=AB﹣AP=(5﹣x)cm
以A,D,P为顶点的三角形与以B,C,P为顶点的三角形相似,
①当AD:PB=PA:BC时,
,
解得x=2或3.
②当AD:BC=PA:PB时,,解得x=3,
∴当A,D,P为顶点的三角形与以B,C,P为顶点的三角形相似,AP的值为2或3.
故答案为2或3.
15.(2019秋?玄武区期末)如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为点P,则DP= 1或或 .
【分析】分三种情况讨论,由相似三角形的性质可求解.
【解析】如图1,若DP∥AB,
∴△CDP∽△CBA,
∴,
∴
∴DP=1;
如图2,若DP∥AC,
∴△BDP∽△BCA,
∴,
∴
∴PD;
如图3,若∠CPD=∠B,且∠C=∠C,
∴△CDP∽△CAB,
∴,
∴,
∴PD,
故答案为:1或或.
16.(2017秋?镇江期末)图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是 Q或G .(写出满足条件的所有的点)
【分析】这个点是点Q或G,根据两边成比例夹角相等即可判断.
【解析】这个点是点Q.
∵∠ABC=∠QDE,,,
∴,
∴△ABC∽QDE,
同法可得:,△ABC∽△EDG,
故答案为Q或G.
17.(2018秋?安庆期中)如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是 秒或秒 .
【分析】如果以点A、D、E为顶点的三角形与△ABC相似,由于A与A对应,那么分两种情况:①D与B对应;②D与C对应.根据相似三角形的性质分别作答.
【解析】如果两点同时运动,设运动t秒时,以点A、D、E为顶点的三角形与△ABC相似,
则AD=t,CE=2t,AE=AC﹣CE=6﹣2t.
①当D与B对应时,有△ADE∽△ABC.
∴AD:AB=AE:AC,
∴t:3=(6﹣2t):6,
∴t;
②当D与C对应时,有△ADE∽△ACB.
∴AD:AC=AE:AB,
∴t:6=(6﹣2t):3,
∴t.
∴当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是秒或秒.
故答案为:秒或秒.
18.(2020秋?宝应县月考)如图,在△ABC中,AB=6cm,AC=8cm,D是AB上一点且AD=2cm,点E在边AC上,当AE= 或1.5 cm时,使得△ADE与△ABC相似.
【分析】分两种情形利用相似三角形的性质求解即可.
【解析】有两种情形:
如图,当DE∥BC时,△ADE∽△ABC,
∴,
∴,
∴AE(cm),
当∠ADE′=∠C时,∵∠A=∠A,
∴△ADE′∽△ACB,
∴,
∴,
∴AE′=1.5(cm),
故答案为或1.5.
三、解答题
19.(2020秋?宝应县月考)如图,在正方形ABCD中,点E在AD上,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)连结BF,若△ABE∽△EBF,试确定点E的位置并说明理由.
【分析】(1)利用“两角法”证得△ABE∽△DEF;
(2)根据相似三角形的对应边成比例解答.
【解答】(1)证明∵四边形ABCD是正方形,
∴∠A=∠D=90°.
∴∠AEB+∠ABE=90°.
∵EF⊥BE,
∴∠AEB+∠DEF=90°.
∴∠ABE=∠DEF.
在△ABE和△DEF中,∠ABE=∠DEF,∠A=∠D,
∴△ABE∽△DEF;
(2)∵△ABE∽△DEF,
∴.
∵△ABE∽△EBF,
∴.
∴.
∴DE=AE.
∴点E为AD的中点.
20.(2020?淮安模拟)如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
【分析】(1)先利用等腰三角形的性质得出∠B=∠C,再由∠BDE=∠CAD可证得△BDE∽△CAD;
(2)先由(1)中相似三角形的性质得∠BED=∠ADC,再利用等角的补角相等,证得∠AED=∠ADB,然后结合两个三角形有一个公共角可证得结论.
【解析】(1)证明:∵AB=AC,
∴∠B=∠C,
又∵∠BDE=∠CAD,
∴△BDE∽△CAD;
(2)证明:∵△BDE∽△CAD,
∴∠BED=∠CDA,
∴180°﹣∠BED=180°﹣∠CDA
即∠AED=∠ADB.
又∵∠BAD=∠DAE,
∴△ADE∽△ABD.
21.(2019秋?宿豫区期末)如图,AD、A′D′分别是△ABC和△A′B′C′的中线,且.判断△ABC和△A′B′C′是否相似,并说明理由.
【分析】根据相似三角形的判定解答即可.
【解析】△ABC∽△A'B'C',
理由:∵
∴△ABD∽△A'B'D',
∴∠B=∠B',
∵AD、A'D'分别是△ABC和△A'B'C'的中线
∴,,
∴,
在△ABC和△A'B'C'中
∵,且∠B=∠B'
∴△ABC∽△A'B'C'.
22.(2019秋?临安区期末)如图,点B、D、E在一条直线上,BE交AC于点F,,且∠BAD=∠CAE.
(1)求证:△ABC∽△ADE;
(2)求证:△AEF∽△BCF.
【分析】(1)根据相似三角形的判定定理证明;
(2)根据相似三角形的性质定理得到∠C=∠E,结合图形,证明即可.
【解答】(1)∵∠BAD=∠CAE
∴∠BAD+∠CAD=∠CAE+∠CAD
即∠BAC=∠DAE
在△ABC和△ADE中
,∠BAC=∠DAE,
∴△ABC∽△ADE;
(2)∵△ABC∽△ADE,
∴∠C=∠E、
在△AEF和△BFC中,∠C=∠E,∠AFE=∠BFC,
∴△AEF∽△BCF.
23.(2018秋?霍邱县期末)如图,在△ABC中,AB=3,AC=4,BC=5,D是AB上的一点,AD=2,在线段AC上是否存在一点E,使A,D,E三点组成的三角形与△ABC相似?如果存在,请求出AE的长;如果不存在,请说明理由.
【分析】由勾股定理的逆定理可得∠BAC=90°,由相似三角形的性质可求解.
【解析】存在,
∵AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∵A,D,E三点组成的三角形与△ABC相似,
∴△ABC∽△ADE或△ABC∽△AED,
∴或,
∴,
∴AE或,
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
