2020-2021学年苏科版九年级数学下册6.5 相似三角形的性质 培优训练(Word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版九年级数学下册6.5 相似三角形的性质 培优训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 804.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 14:50:16 | ||
图片预览




文档简介
6.5 相似三角形的性质 培优训练
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?南京一模)已知△ABC∽△DEF,△ABC与△DEF面积之比为1:4.若BC=1,则EF的长是( )
A. B.2 C.4 D.16
2.(2019秋?海陵区期末)若两个相似三角形的相似比是1:2,则它们的面积比等于( )
A.1: B.1:2 C.1:3 D.1:4
3.(2019秋?新沂市期末)已知△ABC和△A1B1C1相似,相似比为1:2,则△ABC与△A1B1C1的周长的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
4.(2020?南岸区校级模拟)若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为( )
A.3:4 B.4:3 C.:2 D.2:
5.(2019秋?江阴市期中)在Rt△ABC中,如果将△ABC各边长度都扩大3倍,则锐角A的余弦值( )
A.不变化 B.扩大为原来的3倍
C.缩小为原来的 D.扩大为原来的9倍
6.(2020春?高新区期末)如图,E是矩形ABCD中AD边的中点,BE交AC于点F,△AEF的面积为2,则四边形CDEF的面积为( )
A.6 B.8 C.10 D.12
7.(2020秋?宜兴市校级月考)在如图的正方形网格图中,A、B、C、D都是格点,AB、CD相交于点E,则CE:ED的比值为( )
A. B. C. D.
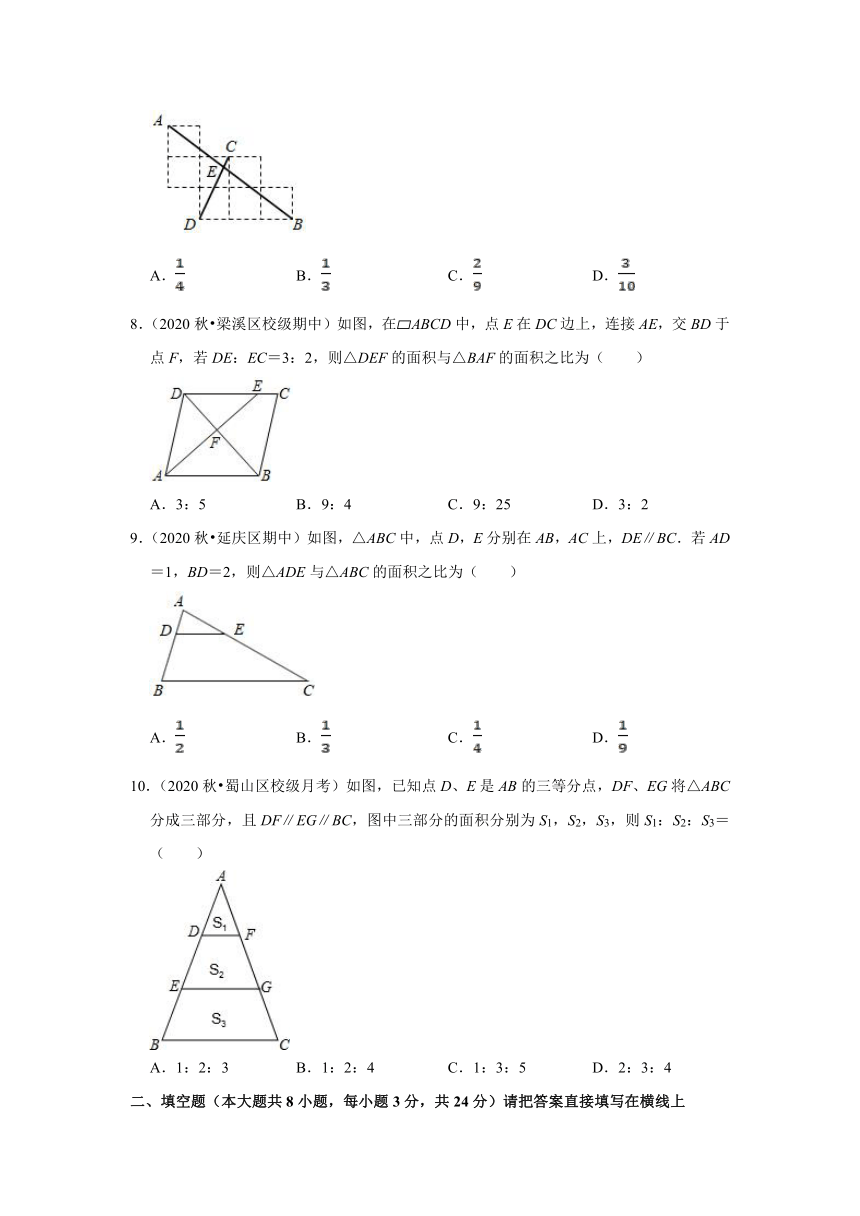
8.(2020秋?梁溪区校级期中)如图,在?ABCD中,点E在DC边上,连接AE,交BD于点F,若DE:EC=3:2,则△DEF的面积与△BAF的面积之比为( )
A.3:5 B.9:4 C.9:25 D.3:2
9.(2020秋?延庆区期中)如图,△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=1,BD=2,则△ADE与△ABC的面积之比为( )
A. B. C. D.
10.(2020秋?蜀山区校级月考)如图,已知点D、E是AB的三等分点,DF、EG将△ABC分成三部分,且DF∥EG∥BC,图中三部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
A.1:2:3 B.1:2:4 C.1:3:5 D.2:3:4
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?淮安模拟)顺次连接三角形三边的中点,所得的三角形与原三角形的相似比是 .
12.(2020?灌云县模拟)若△ABC~△DEF,相似比为3:2,则对应高的比为 .
13.(2019秋?铜山区期末)两个相似三角形的面积比为9:16,其中较大的三角形的周长为64cm,则较小的三角形的周长为 cm.
14.(2020秋?江阴市校级月考)两个相似三角形周长之比为2:3,面积之差为10cm2,则它们的面积之和为 cm2.
15.(2020?鼓楼区校级模拟)如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=1,BD=2,则AC的长 .
16.(2020春?海淀区校级月考)如图,在矩形ABCD中,E是边AB中点,连接DE交AC于点F,若AB=12,AD=9,则CF的长为 .
17.(2019秋?雨花台区期末)如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为 .
18.(2019?丹阳市模拟)如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,∠MON=∠B,若△OMN与△OBC相似,则CM= .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2018秋?兴化市月考)如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
20.(2020春?大丰区期中)如图,已知△ABC中,AT为∠BAC的平分线,
(1)若AB=3,AC=4,BC=5,求△ABT与△ACT的面积之比.
(2)求证:.
21.(2020?鼓楼区校级模拟)如图,O是?ABCD对角线BD上的一点,且∠AOC=2∠ABC,OC=OD,连接OA.
(1)求证:?ABCD是菱形;
(2)求证:CD2=OD?BD.
22.(2018秋?临泽县校级期中)如图所示,在矩形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动时间(0≤t≤6).那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
23.(2019秋?赣榆区期末)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
24.(2020?淮安模拟)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少时,以点C,P,Q为顶点的三角形与△ABC相似?
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?南京一模)已知△ABC∽△DEF,△ABC与△DEF面积之比为1:4.若BC=1,则EF的长是( )
A. B.2 C.4 D.16
【分析】根据相似三角形面积的比等于相似比的平方计算,得到答案.
【解析】∵△ABC∽△DEF,△ABC与△DEF面积之比为1:4,
∴△ABC与△DEF相似比为1:2,即,
∵BC=1,
∴EF=2,
故选:B.
2.(2019秋?海陵区期末)若两个相似三角形的相似比是1:2,则它们的面积比等于( )
A.1: B.1:2 C.1:3 D.1:4
【分析】根据相似三角形的面积比等于相似比的平方计算,得到答案.
【解析】∵两个相似三角形的相似比是1:2,
∴这两个三角形们的面积比为1:4,
故选:D.
3.(2019秋?新沂市期末)已知△ABC和△A1B1C1相似,相似比为1:2,则△ABC与△A1B1C1的周长的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
【分析】根据相似三角形的周长比等于相似比解决问题即可.
【解析】∵△ABC∽△A1B1C1,且相似比为1:2,
∴△ABC与△A1B1C1的周长比为1:2,
故选:A.
4.(2020?南岸区校级模拟)若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为( )
A.3:4 B.4:3 C.:2 D.2:
【分析】由△ABC∽△DEF,S△ABC:S△DEF=3:4,根据相似三角形的面积比等于相似比的平方,即可求得答案.
【解析】∵△ABC∽△DEF,S△ABC:S△DEF=3:4,
∴△ABC与△DEF的相似比为::2,
∴△ABC与△DEF的周长比为::2.
故选:C.
5.(2019秋?江阴市期中)在Rt△ABC中,如果将△ABC各边长度都扩大3倍,则锐角A的余弦值( )
A.不变化 B.扩大为原来的3倍
C.缩小为原来的 D.扩大为原来的9倍
【分析】根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,可得答案.
【解析】Rt△ABC中,cosA,
Rt△ABC中,各边的长度都扩大3倍,那么锐角A的余弦,
cosA.
故选:A.
6.(2020春?高新区期末)如图,E是矩形ABCD中AD边的中点,BE交AC于点F,△AEF的面积为2,则四边形CDEF的面积为( )
A.6 B.8 C.10 D.12
【分析】用矩形的性质得到AD∥BC,BC=AD,再证明△AEF∽△CBF得到,由相似三角形的性质得到S△CBF=4S△AEF=8,利用三角形的面积公式得到S△ABFS△CBF=4,S△ABC=S△ADC=S△CBF+S△ABF=12,然后利用△ADC的面积减去△AEF的面积得到四边CDEF的面积.
【解析】∵四边形ABCD为矩形,
∴AD∥BC,BC=AD,AB=CD,∠ABC=∠D=90°,
∴S△ABC=S△ADC,
∵E是矩形ABCD中AD边的中点,
∴BC=AD=2AE,
∵AE∥BC,
∴△AEF∽△CBF,
∴,
∴()2,
∴S△CBF=4S△AEF=8,
∴S△ABFS△CBF=4,
∴S△ABC=S△ADC=S△CBF+S△ABF=12,
∴四边CDEF的面积为:S△ADC﹣S△AEF=12﹣2=10,
故选:C.
7.(2020秋?宜兴市校级月考)在如图的正方形网格图中,A、B、C、D都是格点,AB、CD相交于点E,则CE:ED的比值为( )
A. B. C. D.
【分析】设小正方形的边长为1,由平行线分线段成比例可求CN,DG的长,通过证明△CEN∽△DEG,可得,可求解.
【解析】如图,过点A作AF⊥BD,交BD的延长线于F,过点C作CH⊥BD于H,设AB与CH的交点为N,与DM交于点G,小正方形的边长为1,
∵AF∥CH,
∴△BNH∽△BAF,
∴,
∴NHAF,
∴CN=CH﹣NH,
∵DM∥AF,
∴,
∴DG,
∵CH∥DM,
∴△CEN∽△DEG,
∴,
故选:C.
8.(2020秋?梁溪区校级期中)如图,在?ABCD中,点E在DC边上,连接AE,交BD于点F,若DE:EC=3:2,则△DEF的面积与△BAF的面积之比为( )
A.3:5 B.9:4 C.9:25 D.3:2
【分析】利用平行四边形的性质得到DC∥AB,DC=AB,则可判断△DEF∽△BAF,然后根据相似三角形的性质求解.
【解析】∵DE:EC=3:2,
∴DE:DC=3:5,
∵四边形ABCD为平行四边形,
∴DC∥AB,DC=AB,
∴DE:AB=3:5,
∵DE∥AB,
∴△DEF∽△BAF,
∴()2=()2.
故选:C.
9.(2020秋?延庆区期中)如图,△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=1,BD=2,则△ADE与△ABC的面积之比为( )
A. B. C. D.
【分析】先证明△ADE∽△ABC,然后根据相似三角形的性质求解.
【解析】∵DE∥BC,
∴△ADE∽△ABC,
∴()2=()2.
故选:D.
10.(2020秋?蜀山区校级月考)如图,已知点D、E是AB的三等分点,DF、EG将△ABC分成三部分,且DF∥EG∥BC,图中三部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
A.1:2:3 B.1:2:4 C.1:3:5 D.2:3:4
【分析】根据相似三角形的判定与性质即可求解.
【解析】∵点D、E是AB的三等分点,
∴,,
∵DF∥EG∥BC,
∴△ADF∽△AEG,△ADF∽△ABC,
∴,,
∴S1:S2:S3=1:3:5,
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?淮安模拟)顺次连接三角形三边的中点,所得的三角形与原三角形的相似比是 1:2 .
【分析】利用三角形的中位线定理得到三角形的相似比即可.
【解析】因为,顺次连接三角形三边的中点,所得的三角形的三边的长等于原三角形对应边的一半,
所以,顺次连接三角形三边的中点,所得的三角形与原三角形对应边的比是 1:2,
所以,所得的三角形与原三角形的相似比为1:2,
故答案为:1:2.
12.(2020?灌云县模拟)若△ABC~△DEF,相似比为3:2,则对应高的比为 3:2 .
【分析】直接利用相似三角形对应高的比等于相似比进而得出答案.
【解析】∵△ABC∽△DEF,相似比为3:2,
∴对应高的比为:3:2.
故答案为:3:2
13.(2019秋?铜山区期末)两个相似三角形的面积比为9:16,其中较大的三角形的周长为64cm,则较小的三角形的周长为 48 cm.
【分析】根据相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方计算即可.
【解析】两个相似多边形的面积比是9:16,
面积比是周长比的平方,
则大多边形与小多边形的相似比是4:3.
相似多边形周长的比等于相似比,
因而设小多边形的周长为xcm,
则有64:x=4:3,
解得x=48,
故答案为:48.
14.(2020秋?江阴市校级月考)两个相似三角形周长之比为2:3,面积之差为10cm2,则它们的面积之和为 26 cm2.
【分析】由两个相似三角形的周长比为2:3,根据相似三角形(多边形)的周长的比等于相似比;相似三角形的面积比等于相似比的平方,即可求得它们的面积比,又由它们的面积之差为10cm2,即可求得答案.
【解析】∵两个相似三角形的周长比为2:3,
∴这两个相似三角形的相似比为2:3,
∴它们的面积比为:4:9,
设此两个三角形的面积分别为4xcm2,9xcm2,
∵它们的面积之差为10cm2,
∴9x﹣4x=10,
解得:x=2,
∴它们的面积之和是:9x+4x=13x=26(cm2).
故答案为:26.
15.(2020?鼓楼区校级模拟)如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=1,BD=2,则AC的长 .
【分析】根据线段垂直平分线的性质得到CD=BD=2,证明△ACD∽△ABC,根据相似三角形的性质计算,得到答案.
【解析】∵BC的垂直平分线MN交AB于点D,
∴CD=BD=2,
∴∠B=∠DCB,AB=AD+BD=3,
∵CD平分∠ACB,
∴∠ACD=∠DCB=∠B,
∵∠A=∠A,
∴△ACD∽△ABC,
∴,
∴AC2=AD×AB=1×3=3,
∴AC,
故答案为:.
16.(2020春?海淀区校级月考)如图,在矩形ABCD中,E是边AB中点,连接DE交AC于点F,若AB=12,AD=9,则CF的长为 10 .
【分析】由勾股定理可求AC的长,通过证明△AEF∽△CDF,可得,可得CF=2AF,即可求解.
【解析】∵四边形ABCD是矩形,
∴AD=BC=9,AB=CD=12,∠B=90°,
∴AC15,
∵E是边AB中点,
∴AE=6,
∵AB∥CD,
∴△AEF∽△CDF,
∴,
∴CF=2AF,
∵AF+CF=AC=15,
∴AF=5,
∴CF=10,
故答案为:10.
17.(2019秋?雨花台区期末)如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为 或或 .
【分析】利用勾股定理计算出AB=5,则△ABC的周长为12,设AD=x,讨论:(1)作DE⊥AC于E,如图1,则AE=6﹣x,利用△ADE∽△ABC得到x:5=(6﹣x):4;(2)作DF⊥BC于E,如图2,则BD=5﹣x,BF=1+x,利用△BDF∽△BAC得到(5﹣x):5=(1+x):3;(3)作DG⊥AC于G,如图3,则AG=6﹣x,利用Rt△ADG∽Rt△ACB得到x:4=(6﹣x):5,然后分别解关于x的方程即可.
【解析】Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB5,
∴△ABC的周长为3+4+5=12,
设AD=x,
(1)作DE⊥AC于E,如图1,则AE=6﹣x,
∵DE∥BC,
∴△ADE∽△ABC,
∴AD:AB=AE:AC,即x:5=(6﹣x):4,解得x;
(2)作DF⊥BC于E,如图2,则BD=5﹣x,BF=6﹣(5﹣x)=1+x,
∵DF∥AC,
∴△BDF∽△BAC,
∴BD:BA=BF:BC,即(5﹣x):5=(1+x):3,解得x;
(3)作DG⊥AB,交BC于G,如图3,则AG=6﹣x,
∵∠DAG=∠CAB,∠ADG=∠C=90°,
∴Rt△ADG∽Rt△ACB,
∴AD:AC=AG:AB,即x:4=(6﹣x):5,解得x,
综上所述,AD的长为或或.
故答案为或或.
18.(2019?丹阳市模拟)如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,∠MON=∠B,若△OMN与△OBC相似,则CM= 或 .
【分析】分两种情形分别求解:①如图1中,当∠MON=∠OMN时.②如图2中,当∠MON=∠ONM时.
【解析】∵∠ACB=90°,AO=OB,
∴OC=OA=OB,
∴∠B=∠OCB,
∵∠MON=∠B,若△OMN与△OBC相似,
∴有两种情形:①如图1中,当∠MON=∠OMN时,
∵∠OMN=∠B,∠OMC+∠OMN=180°,
∴∠OMC+∠B=180°,
∴∠MOB+∠BCM=180°,
∴∠MOB=90°,
∵∠AOM=∠ACB,∠A=∠A,
∴△AOM∽△ACB,
∴,
∴,
∴AM,
∴CM=AC﹣AM=8.
②如图2中,当∠MON=∠ONM时,
∵∠BOC=∠OMN,
∴∠A+∠ACO=∠ACO+∠MOC,
∴∠MOC=∠A,
∵∠MCO=∠ACO,
∴△OCM∽△ACO,
∴OC2=CM?CA,
∴25=CM?8,
∴CM,
故答案为或.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2018秋?兴化市月考)如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
【分析】(1)根据三角形的内角和得到∠ACB=180°﹣∠BAC﹣∠ABC=65°,根据相似三角形的对应角相等即可得到结论;
(2)根据相似三角形的对应边的比相等即可得到结论.
【解析】(1)∵∠BAC=75°,∠ABC=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=65°,
∵△ABC∽△ADE,
∴∠ADE=∠ABC=40°,∠AED=∠ACB=65°;
(2)∵△ABC∽△ADE,
∴,
∵AB=30cm,BD=18cm,BC=20cm,
∴,
∴DE=8(cm).
20.(2020春?大丰区期中)如图,已知△ABC中,AT为∠BAC的平分线,
(1)若AB=3,AC=4,BC=5,求△ABT与△ACT的面积之比.
(2)求证:.
【分析】(1)过T作TD⊥AB,TE⊥AC,垂足分别为D,E,根据角平分线的性质可得TD=TE,再利用三角形的面积公式可证明结论;
(2)设△ABC中BC边上的高为h,根据三角形的面积公式可求解S△ABT:S△ACT=BT:TC,再结合(1)的结论可证明结论.
【解析】(1)过T作TD⊥AB,TE⊥AC,垂足分别为D,E,
∵AT为∠BAC的平分线,
∴TD=TE,
∵S△ABTAB?TD,S△ACTAC?TE,AB=3,AC=4,
∴S△ABT:S△ACT=AB:AC=3:4;
(2)设△ABC中BC边上的高为h,
则S△ABTBT?h,S△ACTTC?h,
∴S△ABT:S△ACT=BT:TC,
由(1)知S△ABT:S△ACT=AB:AC,
∴.
21.(2020?鼓楼区校级模拟)如图,O是?ABCD对角线BD上的一点,且∠AOC=2∠ABC,OC=OD,连接OA.
(1)求证:?ABCD是菱形;
(2)求证:CD2=OD?BD.
【分析】(1)连接AC,交BD与H,由角的数量关系可证OA=OD=OC,由等腰三角形的性质可得OB⊥AC,由菱形的判定可得结论;
(2)通过证明△CDO∽△BDC,可得,可得结论.
【解答】证明:(1)连接AC,交BD与H,
∵OC=OD,
∴∠DCO=∠CDO,
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=∠ADO+∠CDO,AH=CH,
∵∠AOB=∠ADO+∠DAO,∠COB=∠DCO+∠CDO=2∠CDO,∠AOC=2∠ABC,
∴∠AOB+∠COB=2∠ADO+2∠CDO,
∴∠AOB=2∠ADO,
∴∠DAO=∠ADO,
∴OA=OD,
∴OA=OC,
又∵AH=CH,
∴OB⊥AC,
∴平行四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴BC=CD,
∴∠BDC=∠CBD.
由(1)得∠ODC=∠OCD,
∴∠OCD=∠DBC.
在△CDO和△BDC中,
∵∠ODC=∠CDB,∠OCD=∠CBD
∴△CDO∽△BDC.
∴,
即CD2=OD?BD.
22.(2018秋?临泽县校级期中)如图所示,在矩形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动时间(0≤t≤6).那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
【分析】(1)根据题意得出DQ=t,AP=2t,QA=6﹣t,由于△QAP为等腰直角三角形,则6﹣t=2t,求出t的值即可;
(2)由于以点Q、A、P为顶点的三角形与△ABC的对应边不能确定,故应分两种情况进行讨论.
【解析】(1)∵AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D向点A以1厘米/秒的速度移动,
∴DQ=t,AP=2t,QA=6﹣t,
当△QAP为等腰直角三角形即6﹣t=2t,解得t=2;
(2)两种情况:
当时,即,解得t=1.2(秒);
当时,即,解得t=3(秒).
故当经过1.2秒或3秒时,△QAP与△ABC相似.
23.(2019秋?赣榆区期末)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
【分析】(1)根据勾股定理求出AB,分△BPQ∽△BAC、△BPQ∽△BCA两种情况,根据相似三角形的性质列出比例式,计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,BQ=8﹣4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
【解析】(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:;
24.(2020?淮安模拟)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少时,以点C,P,Q为顶点的三角形与△ABC相似?
【分析】(1)在Rt△CPQ中,当t=3,可知CP、CQ的长,运用勾股定理可将PQ的长求出;
(2)由点P,点Q的运动速度和运动时间,又知AC,BC的长,可将CP、CQ用含t的表达式求出,代入直角三角形面积公式S△CPQCP×CQ求解;
(3)应分两种情况:当Rt△CPQ∽Rt△CAB时,根据,可将时间t求出;当Rt△CPQ∽Rt△CBA时,根据,可求出时间t.
【解析】由题意得AP=4t,CQ=2t,则CP=20﹣4t,
(1)当t=3时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ;
(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为Scm2;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=3;
②当Rt△CPQ∽Rt△CBA时,,即,解得t.
因此t=3或t时,以点C、P、Q为顶点的三角形与△ABC相似.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?南京一模)已知△ABC∽△DEF,△ABC与△DEF面积之比为1:4.若BC=1,则EF的长是( )
A. B.2 C.4 D.16
2.(2019秋?海陵区期末)若两个相似三角形的相似比是1:2,则它们的面积比等于( )
A.1: B.1:2 C.1:3 D.1:4
3.(2019秋?新沂市期末)已知△ABC和△A1B1C1相似,相似比为1:2,则△ABC与△A1B1C1的周长的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
4.(2020?南岸区校级模拟)若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为( )
A.3:4 B.4:3 C.:2 D.2:
5.(2019秋?江阴市期中)在Rt△ABC中,如果将△ABC各边长度都扩大3倍,则锐角A的余弦值( )
A.不变化 B.扩大为原来的3倍
C.缩小为原来的 D.扩大为原来的9倍
6.(2020春?高新区期末)如图,E是矩形ABCD中AD边的中点,BE交AC于点F,△AEF的面积为2,则四边形CDEF的面积为( )
A.6 B.8 C.10 D.12
7.(2020秋?宜兴市校级月考)在如图的正方形网格图中,A、B、C、D都是格点,AB、CD相交于点E,则CE:ED的比值为( )
A. B. C. D.
8.(2020秋?梁溪区校级期中)如图,在?ABCD中,点E在DC边上,连接AE,交BD于点F,若DE:EC=3:2,则△DEF的面积与△BAF的面积之比为( )
A.3:5 B.9:4 C.9:25 D.3:2
9.(2020秋?延庆区期中)如图,△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=1,BD=2,则△ADE与△ABC的面积之比为( )
A. B. C. D.
10.(2020秋?蜀山区校级月考)如图,已知点D、E是AB的三等分点,DF、EG将△ABC分成三部分,且DF∥EG∥BC,图中三部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
A.1:2:3 B.1:2:4 C.1:3:5 D.2:3:4
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?淮安模拟)顺次连接三角形三边的中点,所得的三角形与原三角形的相似比是 .
12.(2020?灌云县模拟)若△ABC~△DEF,相似比为3:2,则对应高的比为 .
13.(2019秋?铜山区期末)两个相似三角形的面积比为9:16,其中较大的三角形的周长为64cm,则较小的三角形的周长为 cm.
14.(2020秋?江阴市校级月考)两个相似三角形周长之比为2:3,面积之差为10cm2,则它们的面积之和为 cm2.
15.(2020?鼓楼区校级模拟)如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=1,BD=2,则AC的长 .
16.(2020春?海淀区校级月考)如图,在矩形ABCD中,E是边AB中点,连接DE交AC于点F,若AB=12,AD=9,则CF的长为 .
17.(2019秋?雨花台区期末)如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为 .
18.(2019?丹阳市模拟)如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,∠MON=∠B,若△OMN与△OBC相似,则CM= .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2018秋?兴化市月考)如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
20.(2020春?大丰区期中)如图,已知△ABC中,AT为∠BAC的平分线,
(1)若AB=3,AC=4,BC=5,求△ABT与△ACT的面积之比.
(2)求证:.
21.(2020?鼓楼区校级模拟)如图,O是?ABCD对角线BD上的一点,且∠AOC=2∠ABC,OC=OD,连接OA.
(1)求证:?ABCD是菱形;
(2)求证:CD2=OD?BD.
22.(2018秋?临泽县校级期中)如图所示,在矩形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动时间(0≤t≤6).那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
23.(2019秋?赣榆区期末)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
24.(2020?淮安模拟)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少时,以点C,P,Q为顶点的三角形与△ABC相似?
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?南京一模)已知△ABC∽△DEF,△ABC与△DEF面积之比为1:4.若BC=1,则EF的长是( )
A. B.2 C.4 D.16
【分析】根据相似三角形面积的比等于相似比的平方计算,得到答案.
【解析】∵△ABC∽△DEF,△ABC与△DEF面积之比为1:4,
∴△ABC与△DEF相似比为1:2,即,
∵BC=1,
∴EF=2,
故选:B.
2.(2019秋?海陵区期末)若两个相似三角形的相似比是1:2,则它们的面积比等于( )
A.1: B.1:2 C.1:3 D.1:4
【分析】根据相似三角形的面积比等于相似比的平方计算,得到答案.
【解析】∵两个相似三角形的相似比是1:2,
∴这两个三角形们的面积比为1:4,
故选:D.
3.(2019秋?新沂市期末)已知△ABC和△A1B1C1相似,相似比为1:2,则△ABC与△A1B1C1的周长的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
【分析】根据相似三角形的周长比等于相似比解决问题即可.
【解析】∵△ABC∽△A1B1C1,且相似比为1:2,
∴△ABC与△A1B1C1的周长比为1:2,
故选:A.
4.(2020?南岸区校级模拟)若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为( )
A.3:4 B.4:3 C.:2 D.2:
【分析】由△ABC∽△DEF,S△ABC:S△DEF=3:4,根据相似三角形的面积比等于相似比的平方,即可求得答案.
【解析】∵△ABC∽△DEF,S△ABC:S△DEF=3:4,
∴△ABC与△DEF的相似比为::2,
∴△ABC与△DEF的周长比为::2.
故选:C.
5.(2019秋?江阴市期中)在Rt△ABC中,如果将△ABC各边长度都扩大3倍,则锐角A的余弦值( )
A.不变化 B.扩大为原来的3倍
C.缩小为原来的 D.扩大为原来的9倍
【分析】根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,可得答案.
【解析】Rt△ABC中,cosA,
Rt△ABC中,各边的长度都扩大3倍,那么锐角A的余弦,
cosA.
故选:A.
6.(2020春?高新区期末)如图,E是矩形ABCD中AD边的中点,BE交AC于点F,△AEF的面积为2,则四边形CDEF的面积为( )
A.6 B.8 C.10 D.12
【分析】用矩形的性质得到AD∥BC,BC=AD,再证明△AEF∽△CBF得到,由相似三角形的性质得到S△CBF=4S△AEF=8,利用三角形的面积公式得到S△ABFS△CBF=4,S△ABC=S△ADC=S△CBF+S△ABF=12,然后利用△ADC的面积减去△AEF的面积得到四边CDEF的面积.
【解析】∵四边形ABCD为矩形,
∴AD∥BC,BC=AD,AB=CD,∠ABC=∠D=90°,
∴S△ABC=S△ADC,
∵E是矩形ABCD中AD边的中点,
∴BC=AD=2AE,
∵AE∥BC,
∴△AEF∽△CBF,
∴,
∴()2,
∴S△CBF=4S△AEF=8,
∴S△ABFS△CBF=4,
∴S△ABC=S△ADC=S△CBF+S△ABF=12,
∴四边CDEF的面积为:S△ADC﹣S△AEF=12﹣2=10,
故选:C.
7.(2020秋?宜兴市校级月考)在如图的正方形网格图中,A、B、C、D都是格点,AB、CD相交于点E,则CE:ED的比值为( )
A. B. C. D.
【分析】设小正方形的边长为1,由平行线分线段成比例可求CN,DG的长,通过证明△CEN∽△DEG,可得,可求解.
【解析】如图,过点A作AF⊥BD,交BD的延长线于F,过点C作CH⊥BD于H,设AB与CH的交点为N,与DM交于点G,小正方形的边长为1,
∵AF∥CH,
∴△BNH∽△BAF,
∴,
∴NHAF,
∴CN=CH﹣NH,
∵DM∥AF,
∴,
∴DG,
∵CH∥DM,
∴△CEN∽△DEG,
∴,
故选:C.
8.(2020秋?梁溪区校级期中)如图,在?ABCD中,点E在DC边上,连接AE,交BD于点F,若DE:EC=3:2,则△DEF的面积与△BAF的面积之比为( )
A.3:5 B.9:4 C.9:25 D.3:2
【分析】利用平行四边形的性质得到DC∥AB,DC=AB,则可判断△DEF∽△BAF,然后根据相似三角形的性质求解.
【解析】∵DE:EC=3:2,
∴DE:DC=3:5,
∵四边形ABCD为平行四边形,
∴DC∥AB,DC=AB,
∴DE:AB=3:5,
∵DE∥AB,
∴△DEF∽△BAF,
∴()2=()2.
故选:C.
9.(2020秋?延庆区期中)如图,△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=1,BD=2,则△ADE与△ABC的面积之比为( )
A. B. C. D.
【分析】先证明△ADE∽△ABC,然后根据相似三角形的性质求解.
【解析】∵DE∥BC,
∴△ADE∽△ABC,
∴()2=()2.
故选:D.
10.(2020秋?蜀山区校级月考)如图,已知点D、E是AB的三等分点,DF、EG将△ABC分成三部分,且DF∥EG∥BC,图中三部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
A.1:2:3 B.1:2:4 C.1:3:5 D.2:3:4
【分析】根据相似三角形的判定与性质即可求解.
【解析】∵点D、E是AB的三等分点,
∴,,
∵DF∥EG∥BC,
∴△ADF∽△AEG,△ADF∽△ABC,
∴,,
∴S1:S2:S3=1:3:5,
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?淮安模拟)顺次连接三角形三边的中点,所得的三角形与原三角形的相似比是 1:2 .
【分析】利用三角形的中位线定理得到三角形的相似比即可.
【解析】因为,顺次连接三角形三边的中点,所得的三角形的三边的长等于原三角形对应边的一半,
所以,顺次连接三角形三边的中点,所得的三角形与原三角形对应边的比是 1:2,
所以,所得的三角形与原三角形的相似比为1:2,
故答案为:1:2.
12.(2020?灌云县模拟)若△ABC~△DEF,相似比为3:2,则对应高的比为 3:2 .
【分析】直接利用相似三角形对应高的比等于相似比进而得出答案.
【解析】∵△ABC∽△DEF,相似比为3:2,
∴对应高的比为:3:2.
故答案为:3:2
13.(2019秋?铜山区期末)两个相似三角形的面积比为9:16,其中较大的三角形的周长为64cm,则较小的三角形的周长为 48 cm.
【分析】根据相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方计算即可.
【解析】两个相似多边形的面积比是9:16,
面积比是周长比的平方,
则大多边形与小多边形的相似比是4:3.
相似多边形周长的比等于相似比,
因而设小多边形的周长为xcm,
则有64:x=4:3,
解得x=48,
故答案为:48.
14.(2020秋?江阴市校级月考)两个相似三角形周长之比为2:3,面积之差为10cm2,则它们的面积之和为 26 cm2.
【分析】由两个相似三角形的周长比为2:3,根据相似三角形(多边形)的周长的比等于相似比;相似三角形的面积比等于相似比的平方,即可求得它们的面积比,又由它们的面积之差为10cm2,即可求得答案.
【解析】∵两个相似三角形的周长比为2:3,
∴这两个相似三角形的相似比为2:3,
∴它们的面积比为:4:9,
设此两个三角形的面积分别为4xcm2,9xcm2,
∵它们的面积之差为10cm2,
∴9x﹣4x=10,
解得:x=2,
∴它们的面积之和是:9x+4x=13x=26(cm2).
故答案为:26.
15.(2020?鼓楼区校级模拟)如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=1,BD=2,则AC的长 .
【分析】根据线段垂直平分线的性质得到CD=BD=2,证明△ACD∽△ABC,根据相似三角形的性质计算,得到答案.
【解析】∵BC的垂直平分线MN交AB于点D,
∴CD=BD=2,
∴∠B=∠DCB,AB=AD+BD=3,
∵CD平分∠ACB,
∴∠ACD=∠DCB=∠B,
∵∠A=∠A,
∴△ACD∽△ABC,
∴,
∴AC2=AD×AB=1×3=3,
∴AC,
故答案为:.
16.(2020春?海淀区校级月考)如图,在矩形ABCD中,E是边AB中点,连接DE交AC于点F,若AB=12,AD=9,则CF的长为 10 .
【分析】由勾股定理可求AC的长,通过证明△AEF∽△CDF,可得,可得CF=2AF,即可求解.
【解析】∵四边形ABCD是矩形,
∴AD=BC=9,AB=CD=12,∠B=90°,
∴AC15,
∵E是边AB中点,
∴AE=6,
∵AB∥CD,
∴△AEF∽△CDF,
∴,
∴CF=2AF,
∵AF+CF=AC=15,
∴AF=5,
∴CF=10,
故答案为:10.
17.(2019秋?雨花台区期末)如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为 或或 .
【分析】利用勾股定理计算出AB=5,则△ABC的周长为12,设AD=x,讨论:(1)作DE⊥AC于E,如图1,则AE=6﹣x,利用△ADE∽△ABC得到x:5=(6﹣x):4;(2)作DF⊥BC于E,如图2,则BD=5﹣x,BF=1+x,利用△BDF∽△BAC得到(5﹣x):5=(1+x):3;(3)作DG⊥AC于G,如图3,则AG=6﹣x,利用Rt△ADG∽Rt△ACB得到x:4=(6﹣x):5,然后分别解关于x的方程即可.
【解析】Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB5,
∴△ABC的周长为3+4+5=12,
设AD=x,
(1)作DE⊥AC于E,如图1,则AE=6﹣x,
∵DE∥BC,
∴△ADE∽△ABC,
∴AD:AB=AE:AC,即x:5=(6﹣x):4,解得x;
(2)作DF⊥BC于E,如图2,则BD=5﹣x,BF=6﹣(5﹣x)=1+x,
∵DF∥AC,
∴△BDF∽△BAC,
∴BD:BA=BF:BC,即(5﹣x):5=(1+x):3,解得x;
(3)作DG⊥AB,交BC于G,如图3,则AG=6﹣x,
∵∠DAG=∠CAB,∠ADG=∠C=90°,
∴Rt△ADG∽Rt△ACB,
∴AD:AC=AG:AB,即x:4=(6﹣x):5,解得x,
综上所述,AD的长为或或.
故答案为或或.
18.(2019?丹阳市模拟)如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,∠MON=∠B,若△OMN与△OBC相似,则CM= 或 .
【分析】分两种情形分别求解:①如图1中,当∠MON=∠OMN时.②如图2中,当∠MON=∠ONM时.
【解析】∵∠ACB=90°,AO=OB,
∴OC=OA=OB,
∴∠B=∠OCB,
∵∠MON=∠B,若△OMN与△OBC相似,
∴有两种情形:①如图1中,当∠MON=∠OMN时,
∵∠OMN=∠B,∠OMC+∠OMN=180°,
∴∠OMC+∠B=180°,
∴∠MOB+∠BCM=180°,
∴∠MOB=90°,
∵∠AOM=∠ACB,∠A=∠A,
∴△AOM∽△ACB,
∴,
∴,
∴AM,
∴CM=AC﹣AM=8.
②如图2中,当∠MON=∠ONM时,
∵∠BOC=∠OMN,
∴∠A+∠ACO=∠ACO+∠MOC,
∴∠MOC=∠A,
∵∠MCO=∠ACO,
∴△OCM∽△ACO,
∴OC2=CM?CA,
∴25=CM?8,
∴CM,
故答案为或.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2018秋?兴化市月考)如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
【分析】(1)根据三角形的内角和得到∠ACB=180°﹣∠BAC﹣∠ABC=65°,根据相似三角形的对应角相等即可得到结论;
(2)根据相似三角形的对应边的比相等即可得到结论.
【解析】(1)∵∠BAC=75°,∠ABC=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=65°,
∵△ABC∽△ADE,
∴∠ADE=∠ABC=40°,∠AED=∠ACB=65°;
(2)∵△ABC∽△ADE,
∴,
∵AB=30cm,BD=18cm,BC=20cm,
∴,
∴DE=8(cm).
20.(2020春?大丰区期中)如图,已知△ABC中,AT为∠BAC的平分线,
(1)若AB=3,AC=4,BC=5,求△ABT与△ACT的面积之比.
(2)求证:.
【分析】(1)过T作TD⊥AB,TE⊥AC,垂足分别为D,E,根据角平分线的性质可得TD=TE,再利用三角形的面积公式可证明结论;
(2)设△ABC中BC边上的高为h,根据三角形的面积公式可求解S△ABT:S△ACT=BT:TC,再结合(1)的结论可证明结论.
【解析】(1)过T作TD⊥AB,TE⊥AC,垂足分别为D,E,
∵AT为∠BAC的平分线,
∴TD=TE,
∵S△ABTAB?TD,S△ACTAC?TE,AB=3,AC=4,
∴S△ABT:S△ACT=AB:AC=3:4;
(2)设△ABC中BC边上的高为h,
则S△ABTBT?h,S△ACTTC?h,
∴S△ABT:S△ACT=BT:TC,
由(1)知S△ABT:S△ACT=AB:AC,
∴.
21.(2020?鼓楼区校级模拟)如图,O是?ABCD对角线BD上的一点,且∠AOC=2∠ABC,OC=OD,连接OA.
(1)求证:?ABCD是菱形;
(2)求证:CD2=OD?BD.
【分析】(1)连接AC,交BD与H,由角的数量关系可证OA=OD=OC,由等腰三角形的性质可得OB⊥AC,由菱形的判定可得结论;
(2)通过证明△CDO∽△BDC,可得,可得结论.
【解答】证明:(1)连接AC,交BD与H,
∵OC=OD,
∴∠DCO=∠CDO,
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=∠ADO+∠CDO,AH=CH,
∵∠AOB=∠ADO+∠DAO,∠COB=∠DCO+∠CDO=2∠CDO,∠AOC=2∠ABC,
∴∠AOB+∠COB=2∠ADO+2∠CDO,
∴∠AOB=2∠ADO,
∴∠DAO=∠ADO,
∴OA=OD,
∴OA=OC,
又∵AH=CH,
∴OB⊥AC,
∴平行四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴BC=CD,
∴∠BDC=∠CBD.
由(1)得∠ODC=∠OCD,
∴∠OCD=∠DBC.
在△CDO和△BDC中,
∵∠ODC=∠CDB,∠OCD=∠CBD
∴△CDO∽△BDC.
∴,
即CD2=OD?BD.
22.(2018秋?临泽县校级期中)如图所示,在矩形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动时间(0≤t≤6).那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
【分析】(1)根据题意得出DQ=t,AP=2t,QA=6﹣t,由于△QAP为等腰直角三角形,则6﹣t=2t,求出t的值即可;
(2)由于以点Q、A、P为顶点的三角形与△ABC的对应边不能确定,故应分两种情况进行讨论.
【解析】(1)∵AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D向点A以1厘米/秒的速度移动,
∴DQ=t,AP=2t,QA=6﹣t,
当△QAP为等腰直角三角形即6﹣t=2t,解得t=2;
(2)两种情况:
当时,即,解得t=1.2(秒);
当时,即,解得t=3(秒).
故当经过1.2秒或3秒时,△QAP与△ABC相似.
23.(2019秋?赣榆区期末)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
【分析】(1)根据勾股定理求出AB,分△BPQ∽△BAC、△BPQ∽△BCA两种情况,根据相似三角形的性质列出比例式,计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,BQ=8﹣4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
【解析】(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:;
24.(2020?淮安模拟)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少时,以点C,P,Q为顶点的三角形与△ABC相似?
【分析】(1)在Rt△CPQ中,当t=3,可知CP、CQ的长,运用勾股定理可将PQ的长求出;
(2)由点P,点Q的运动速度和运动时间,又知AC,BC的长,可将CP、CQ用含t的表达式求出,代入直角三角形面积公式S△CPQCP×CQ求解;
(3)应分两种情况:当Rt△CPQ∽Rt△CAB时,根据,可将时间t求出;当Rt△CPQ∽Rt△CBA时,根据,可求出时间t.
【解析】由题意得AP=4t,CQ=2t,则CP=20﹣4t,
(1)当t=3时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ;
(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为Scm2;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=3;
②当Rt△CPQ∽Rt△CBA时,,即,解得t.
因此t=3或t时,以点C、P、Q为顶点的三角形与△ABC相似.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
