2020-2021学年湘教新版八年级下册数学期末冲刺试题(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年湘教新版八年级下册数学期末冲刺试题(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 271.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 14:59:11 | ||
图片预览




文档简介
2020-2021学年湘教新版八年级下册数学期末冲刺试题
一.填空题(共8小题,满分32分,每小题4分)
1.函数y=中,自变量x的取值范围是
.
2.计算:÷=
.
3.三角形的三边长分别为3,4,5,则这个三角形的面积是
.
4.一次函数y=(m﹣3)x﹣2的图象经过二、三、四象限,则m的取值范围是
.
5.请写出一个过第二、四象限的正比例函数的解析式
.
6.菱形ABCD中,对角线AC长为10cm,BD=6cm,则菱形ABCD的面积为
cm2.
7.某校九年级进行了3次数学模拟考试,甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分,方差分别是,,,,则这4名同学3次数学成绩最稳定的是
.
8.若点P(2,3)在一次函数y=2x﹣m的图象上,则m的值为
.
二.选择题(共10小题,满分40分,每小题4分)
9.下列各式,化简后能与合并的是( )
A.
B.
C.
D.
10.以下列长度的三条线段为边,能组成直角三角形的是( )
A.6,7,8
B.2,3,4
C.3,4,6
D.6,8,10
11.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC
B.AC=BD
C.∠A=∠C
D.∠A=∠B
12.下列计算正确的是( )
A.3﹣=3
B.2+=2
C.=﹣2
D.=2
13.如图所示的图形中,属于多边形的有( )个.
A.3
B.4
C.5
D.6
14.如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
A.3
B.4
C.2
D.3
15.如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,DE⊥AB,且AC=6cm,AB=8cm,则△ADE的周长为( )
A.8cm
B.10cm
C.12cm
D.14cm
16.如图,?ABCD的周长为36cm,△ABC的周长为28cm,则对角线AC的长为( )
A.28cm
B.18cm
C.10cm
D.8cm
17.某女子排球队6名场上队员的身高(单位:cm)是:170,174,178,180,180,184.现用身高为178cm的队员替换场上身高为174cm的队员,与换人前相比,场上队员的身高( )
A.平均数变大,中位数不变
B.平均数变大,中位数变大
C.平均数变小,中位数不变
D.平均数变小,中位数变大
18.在平面直角坐标系中,将一次函数y=2x+1的图象向左平移1个单位长度,得到的图象对应的函数表达式是( )
A.y=2x+2
B.y=2x+3
C.y=2x
D.y=2x﹣1
三.解答题(共8小题,满分78分)
19.计算:(﹣)÷+.
20.如图,在?ABCD中,点E、F分别是AD、BC的中点,求证:AF=CE.
21.在四边形ABCD中,∠B=∠D=90°,∠DCB=60°,AB=3.AD=5,求对角线AC的长.
22.已知直线y=kx+b经过点(3,3)和(﹣1,1),求该直线的解析式.
23.小明本学期的数学成绩如表所示:
测验类别
平时成绩1
平时成绩2
平时成绩3
平时成绩4
平时平均数
期中考试
期末考试
成绩
108
103
101
108
a
110
114
(1)六次测试成绩的中位数和众数分别是什么?
(2)请计算出小明该学期的平时成绩平均分a的值;
(3)如果学期的数学总评成绩是根据一定的权重计算所得,其中平时成绩a所占权重为20%,已知小明该学期的总评成绩为111分,请计算出期中考试和期末考试各自所占权重.
24.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.
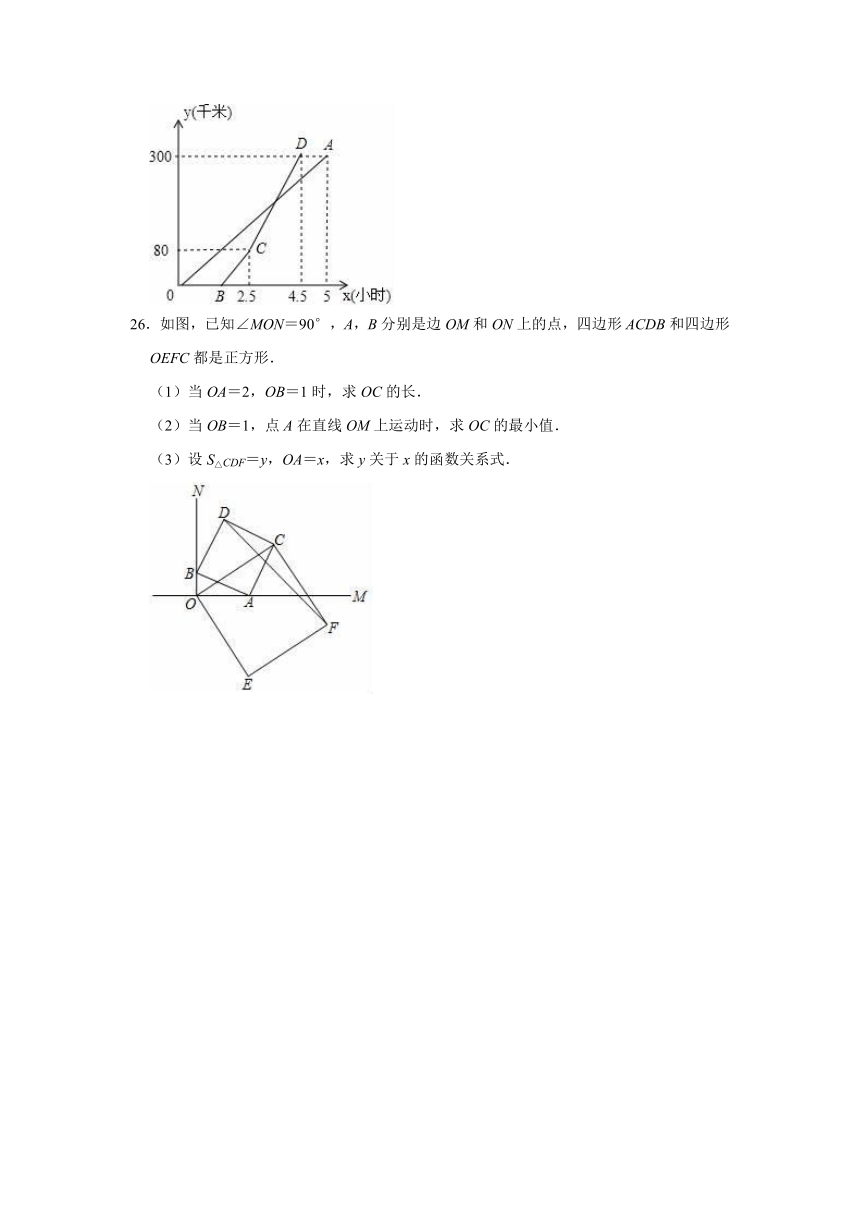
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
26.如图,已知∠MON=90°,A,B分别是边OM和ON上的点,四边形ACDB和四边形OEFC都是正方形.
(1)当OA=2,OB=1时,求OC的长.
(2)当OB=1,点A在直线OM上运动时,求OC的最小值.
(3)设S△CDF=y,OA=x,求y关于x的函数关系式.
参考答案与试题解析
一.填空题(共8小题,满分32分,每小题4分)
1.解:根据题意,得:,
解得:x≤2且x≠﹣2,
故答案为:x≤2且x≠﹣2.
2.解:原式===.
故答案为:.
3.解:∵三角形的三边长分别为3,4,5,
∴52=32+42,
∴此三角形为直角三角形,
∴这个三角形的面积=×3×4=6.
故答案为:6.
4.解:∵一次函数y=(m﹣3)x﹣2的图象经过二、三、四象限,
∴m﹣3<0,
∴m<3,
故答案为:m<3
5.解:正比例函数y=﹣x的图象经过第二、四象限.
故答案为:y=﹣x(答案不唯一).
6.解:菱形的面积等于两对角线的积的一半,则这个菱形的面积是6×10×=30cm2.
故答案为30.
7.解:∵s甲2=3.6,s乙2=4.6,s丙2=6.3,s丁2=7.3,且平均数相等,
∴s甲2<s乙2<s丙2<s丁2,
∴这4名同学3次数学成绩最稳定的是甲,
故答案为甲.
8.解:∵一次函数y=2x﹣m的图象经过点P(2,3),
∴3=4﹣m,
解得m=1,
故答案为:1
二.选择题(共10小题,满分40分,每小题4分)
9.解:与是同类二次根式即可合并,
由于=2,2与是同类二次根式,
∴2与可以合并,
故选:C.
10.解:A、∵62+72≠82,∴不能构成直角三角形,故本选项错误;
B、∵22+32≠42,∴不能构成直角三角形,故本选项错误;
C、∵32+42≠62,∴不能构成直角三角形,故本选项错误;
D、∵62+82=102,∴能构成直角三角形,故本选项正确.
故选:D.
11.解:如图所示:∵AB∥CD,
∴∠B+∠C=180°,
当∠A=∠C时,则∠A+∠B=180°,
故AD∥BC,
则四边形ABCD是平行四边形.
故选:C.
12.解:A、3﹣=2,故此选项错误;
B、2+无法计算,故此选项错误;
C、=2,故此选项错误;
D、=2,正确.
故选:D.
13.解:所示的图形中,属于多边形的有第一个、第二个、第五个.
故选:A.
14.解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD=6,
∴AO=OB=3,
∵∠ABO=60°,
∴△AOB是等边三角形,
∴AB=3=OA,
∴AD===3,
故选:A.
15.解:∵DE⊥AB,∠BAC=90°,
∴DE∥AC,
∵D为BC的中点,
∴DE为Rt△ABC的中位线,
∵AC=6cm,AB=8cm.
∴DE=AC=3,AE=4,AD=BC,BC==10,
∴AD=5,
∴△ADE的周长为+AE+AD=12cm.
故选:C.
16.解:∵?ABCD的周长是36cm,
∴AB+AD=18m,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=(AB+BC+AC)﹣(AB+AC)=28﹣18=10(cm).
故选:C.
17.解:用身高为178cm的队员替换场上身高为174cm的队员,使总身高增加,进而平均数身高变大,
但换人后,从小到大排列的顺序不变,因此中位数不变,
故选:A.
18.解:由“左加右减”的原则可知,将一次函数y=2x+1的图象向左平移1个单位,所得图象的解析式为y=2(x+1)+1,即y=2x+3.
故选:B.
三.解答题(共8小题,满分78分)
19.解:原式=﹣+
=2﹣+
=.
20.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC;
又∵点E、F分别是AD、BC的中点,
∴AE∥CF,AE=AD,CF=BC,
∴AE=CF,
∴四边形AECF为平行四边形(对边平行且相等的四边形为平行四边形),
∴AF=CE(平行四边形的对边相等).
21.解:延长BA,CD相交于点E,如图所示:
∵∠B=90°,∠DCB=60°,
∴∠E=30°,
∵∠ADE=90°,AD=5,
∴AE=2AD=10,
∴BE=AB+AE=3+10=13,
∵∠B=90°,∠E=30°,
∴BC=BE?tan∠E=13×=,
∴AC===.
22.解:设该直线的解析式为y=kx+b,
把(3,3),(﹣1,1)代入得:,
解得
∴该直线的解析式为.
23.解:(1)六次数据依次为:101、103、108、108、110、114,
则中位数为:108,众数为:108;
(2)a==105;
(3)设期中考试所占权重是x,期末考试所占权重是y,
由题意得,
解得:.
答:期中考试所占权重是30%,期末考试所占权重是50%.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵OA=OB,
∴OA=OB=OC=OD,
∴AC=BD,
∴四边形ABCD是矩形;
(2)∵∠AOB=120°,OA=OB,
∴∠OAB=∠OBA=30°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=2BC,
∴AB==BC,
∴BC=AB=6×=2.
25.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
26.解:(1)如图1所示,过点C作CG⊥OM于点G,
∵四边形ACDB是正方形,
∴AB=AC,∠BAC=90°,
∵∠MON=90°,∠AGC=90°,
∴∠BAO+∠ABO=90°,∠BAO+∠CAG=90°,
∴∠ABO=∠CAG,
∴△AOB≌△AGC(AAS).
∵OA=2,OB=1,
∴CG=OA=2,AG=OB=1,
∴OG=3,
∴在Rt△OGC中,由勾股定理得:
OC==.
(2)如图2所示,由题意可得点C在直线l:y=x﹣1上运动,
∴OC的最小值为当OC与直线l垂直时,此时OC=,
∴OC的最小值为.
(3)如图3所示,延长OC至点H,使CH=OC,连接AH,过点C作CG⊥OM,
∵CD=CA,CH=CF,∠DCF=∠ACH=90°+∠ACF,
∴△DCF≌△ACH(SAS),
由(1)知△AOB≌△AGC(AAS),
∴CG=OA,
∵C是OH的中点,
∴S△ACH=S△OAC,
∵S△CDF=y,OA=x,
∴y=S△OAH
=S△OAC
=x2.
∴y关于x的函数关系式为y=x2.
一.填空题(共8小题,满分32分,每小题4分)
1.函数y=中,自变量x的取值范围是
.
2.计算:÷=
.
3.三角形的三边长分别为3,4,5,则这个三角形的面积是
.
4.一次函数y=(m﹣3)x﹣2的图象经过二、三、四象限,则m的取值范围是
.
5.请写出一个过第二、四象限的正比例函数的解析式
.
6.菱形ABCD中,对角线AC长为10cm,BD=6cm,则菱形ABCD的面积为
cm2.
7.某校九年级进行了3次数学模拟考试,甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分,方差分别是,,,,则这4名同学3次数学成绩最稳定的是
.
8.若点P(2,3)在一次函数y=2x﹣m的图象上,则m的值为
.
二.选择题(共10小题,满分40分,每小题4分)
9.下列各式,化简后能与合并的是( )
A.
B.
C.
D.
10.以下列长度的三条线段为边,能组成直角三角形的是( )
A.6,7,8
B.2,3,4
C.3,4,6
D.6,8,10
11.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC
B.AC=BD
C.∠A=∠C
D.∠A=∠B
12.下列计算正确的是( )
A.3﹣=3
B.2+=2
C.=﹣2
D.=2
13.如图所示的图形中,属于多边形的有( )个.
A.3
B.4
C.5
D.6
14.如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
A.3
B.4
C.2
D.3
15.如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,DE⊥AB,且AC=6cm,AB=8cm,则△ADE的周长为( )
A.8cm
B.10cm
C.12cm
D.14cm
16.如图,?ABCD的周长为36cm,△ABC的周长为28cm,则对角线AC的长为( )
A.28cm
B.18cm
C.10cm
D.8cm
17.某女子排球队6名场上队员的身高(单位:cm)是:170,174,178,180,180,184.现用身高为178cm的队员替换场上身高为174cm的队员,与换人前相比,场上队员的身高( )
A.平均数变大,中位数不变
B.平均数变大,中位数变大
C.平均数变小,中位数不变
D.平均数变小,中位数变大
18.在平面直角坐标系中,将一次函数y=2x+1的图象向左平移1个单位长度,得到的图象对应的函数表达式是( )
A.y=2x+2
B.y=2x+3
C.y=2x
D.y=2x﹣1
三.解答题(共8小题,满分78分)
19.计算:(﹣)÷+.
20.如图,在?ABCD中,点E、F分别是AD、BC的中点,求证:AF=CE.
21.在四边形ABCD中,∠B=∠D=90°,∠DCB=60°,AB=3.AD=5,求对角线AC的长.
22.已知直线y=kx+b经过点(3,3)和(﹣1,1),求该直线的解析式.
23.小明本学期的数学成绩如表所示:
测验类别
平时成绩1
平时成绩2
平时成绩3
平时成绩4
平时平均数
期中考试
期末考试
成绩
108
103
101
108
a
110
114
(1)六次测试成绩的中位数和众数分别是什么?
(2)请计算出小明该学期的平时成绩平均分a的值;
(3)如果学期的数学总评成绩是根据一定的权重计算所得,其中平时成绩a所占权重为20%,已知小明该学期的总评成绩为111分,请计算出期中考试和期末考试各自所占权重.
24.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
26.如图,已知∠MON=90°,A,B分别是边OM和ON上的点,四边形ACDB和四边形OEFC都是正方形.
(1)当OA=2,OB=1时,求OC的长.
(2)当OB=1,点A在直线OM上运动时,求OC的最小值.
(3)设S△CDF=y,OA=x,求y关于x的函数关系式.
参考答案与试题解析
一.填空题(共8小题,满分32分,每小题4分)
1.解:根据题意,得:,
解得:x≤2且x≠﹣2,
故答案为:x≤2且x≠﹣2.
2.解:原式===.
故答案为:.
3.解:∵三角形的三边长分别为3,4,5,
∴52=32+42,
∴此三角形为直角三角形,
∴这个三角形的面积=×3×4=6.
故答案为:6.
4.解:∵一次函数y=(m﹣3)x﹣2的图象经过二、三、四象限,
∴m﹣3<0,
∴m<3,
故答案为:m<3
5.解:正比例函数y=﹣x的图象经过第二、四象限.
故答案为:y=﹣x(答案不唯一).
6.解:菱形的面积等于两对角线的积的一半,则这个菱形的面积是6×10×=30cm2.
故答案为30.
7.解:∵s甲2=3.6,s乙2=4.6,s丙2=6.3,s丁2=7.3,且平均数相等,
∴s甲2<s乙2<s丙2<s丁2,
∴这4名同学3次数学成绩最稳定的是甲,
故答案为甲.
8.解:∵一次函数y=2x﹣m的图象经过点P(2,3),
∴3=4﹣m,
解得m=1,
故答案为:1
二.选择题(共10小题,满分40分,每小题4分)
9.解:与是同类二次根式即可合并,
由于=2,2与是同类二次根式,
∴2与可以合并,
故选:C.
10.解:A、∵62+72≠82,∴不能构成直角三角形,故本选项错误;
B、∵22+32≠42,∴不能构成直角三角形,故本选项错误;
C、∵32+42≠62,∴不能构成直角三角形,故本选项错误;
D、∵62+82=102,∴能构成直角三角形,故本选项正确.
故选:D.
11.解:如图所示:∵AB∥CD,
∴∠B+∠C=180°,
当∠A=∠C时,则∠A+∠B=180°,
故AD∥BC,
则四边形ABCD是平行四边形.
故选:C.
12.解:A、3﹣=2,故此选项错误;
B、2+无法计算,故此选项错误;
C、=2,故此选项错误;
D、=2,正确.
故选:D.
13.解:所示的图形中,属于多边形的有第一个、第二个、第五个.
故选:A.
14.解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD=6,
∴AO=OB=3,
∵∠ABO=60°,
∴△AOB是等边三角形,
∴AB=3=OA,
∴AD===3,
故选:A.
15.解:∵DE⊥AB,∠BAC=90°,
∴DE∥AC,
∵D为BC的中点,
∴DE为Rt△ABC的中位线,
∵AC=6cm,AB=8cm.
∴DE=AC=3,AE=4,AD=BC,BC==10,
∴AD=5,
∴△ADE的周长为+AE+AD=12cm.
故选:C.
16.解:∵?ABCD的周长是36cm,
∴AB+AD=18m,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=(AB+BC+AC)﹣(AB+AC)=28﹣18=10(cm).
故选:C.
17.解:用身高为178cm的队员替换场上身高为174cm的队员,使总身高增加,进而平均数身高变大,
但换人后,从小到大排列的顺序不变,因此中位数不变,
故选:A.
18.解:由“左加右减”的原则可知,将一次函数y=2x+1的图象向左平移1个单位,所得图象的解析式为y=2(x+1)+1,即y=2x+3.
故选:B.
三.解答题(共8小题,满分78分)
19.解:原式=﹣+
=2﹣+
=.
20.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC;
又∵点E、F分别是AD、BC的中点,
∴AE∥CF,AE=AD,CF=BC,
∴AE=CF,
∴四边形AECF为平行四边形(对边平行且相等的四边形为平行四边形),
∴AF=CE(平行四边形的对边相等).
21.解:延长BA,CD相交于点E,如图所示:
∵∠B=90°,∠DCB=60°,
∴∠E=30°,
∵∠ADE=90°,AD=5,
∴AE=2AD=10,
∴BE=AB+AE=3+10=13,
∵∠B=90°,∠E=30°,
∴BC=BE?tan∠E=13×=,
∴AC===.
22.解:设该直线的解析式为y=kx+b,
把(3,3),(﹣1,1)代入得:,
解得
∴该直线的解析式为.
23.解:(1)六次数据依次为:101、103、108、108、110、114,
则中位数为:108,众数为:108;
(2)a==105;
(3)设期中考试所占权重是x,期末考试所占权重是y,
由题意得,
解得:.
答:期中考试所占权重是30%,期末考试所占权重是50%.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵OA=OB,
∴OA=OB=OC=OD,
∴AC=BD,
∴四边形ABCD是矩形;
(2)∵∠AOB=120°,OA=OB,
∴∠OAB=∠OBA=30°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=2BC,
∴AB==BC,
∴BC=AB=6×=2.
25.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
26.解:(1)如图1所示,过点C作CG⊥OM于点G,
∵四边形ACDB是正方形,
∴AB=AC,∠BAC=90°,
∵∠MON=90°,∠AGC=90°,
∴∠BAO+∠ABO=90°,∠BAO+∠CAG=90°,
∴∠ABO=∠CAG,
∴△AOB≌△AGC(AAS).
∵OA=2,OB=1,
∴CG=OA=2,AG=OB=1,
∴OG=3,
∴在Rt△OGC中,由勾股定理得:
OC==.
(2)如图2所示,由题意可得点C在直线l:y=x﹣1上运动,
∴OC的最小值为当OC与直线l垂直时,此时OC=,
∴OC的最小值为.
(3)如图3所示,延长OC至点H,使CH=OC,连接AH,过点C作CG⊥OM,
∵CD=CA,CH=CF,∠DCF=∠ACH=90°+∠ACF,
∴△DCF≌△ACH(SAS),
由(1)知△AOB≌△AGC(AAS),
∴CG=OA,
∵C是OH的中点,
∴S△ACH=S△OAC,
∵S△CDF=y,OA=x,
∴y=S△OAH
=S△OAC
=x2.
∴y关于x的函数关系式为y=x2.
同课章节目录
