五年级上册数学八 用字母表示数 复习课件 苏教版(共43张PPT)
文档属性
| 名称 | 五年级上册数学八 用字母表示数 复习课件 苏教版(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-12 16:25:15 | ||
图片预览







文档简介
(共43张PPT)
八 用字母表示数
复习课件
用字母表示数
用含字母的式子表示简单的数量关系
用含字母的式子表示较复杂的数量关系
化简含有字母的式子
复习旧知
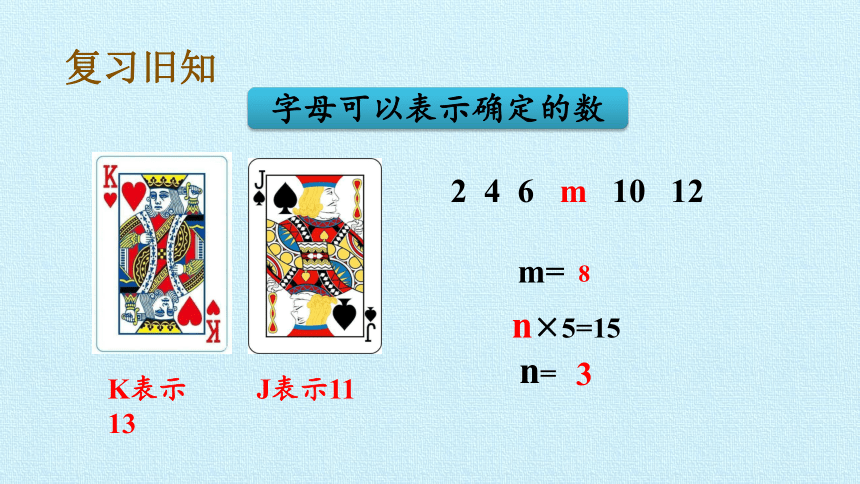
字母可以表示确定的数
K表示13
J表示11
2 4 6 m 10 12
m=
8
n×5=15
n=
3
用字母表示运算律
加法交换律:a+b=b+a
加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:a×b×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c
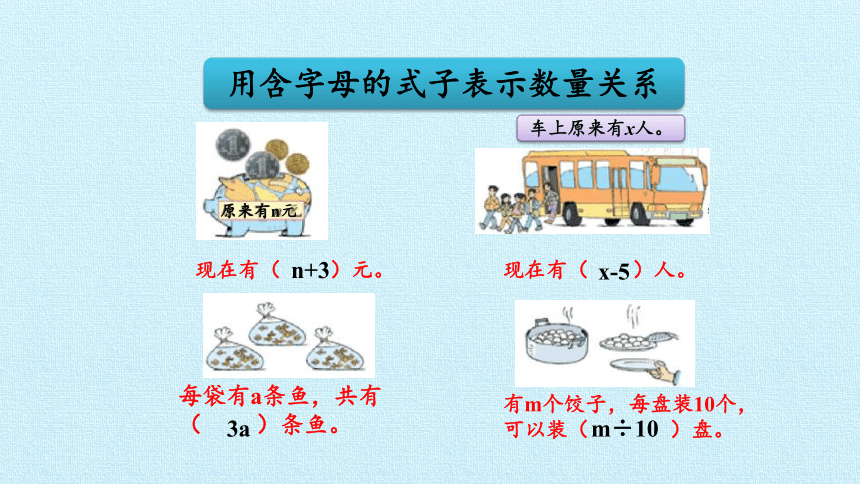
用含字母的式子表示数量关系
原来有n元
现在有( )元。
车上原来有x人。
现在有( )人。
每袋有a条鱼,共有
( )条鱼。
有m个饺子,每盘装10个,可以装( )盘。
n+3
x-5
3a
m÷10
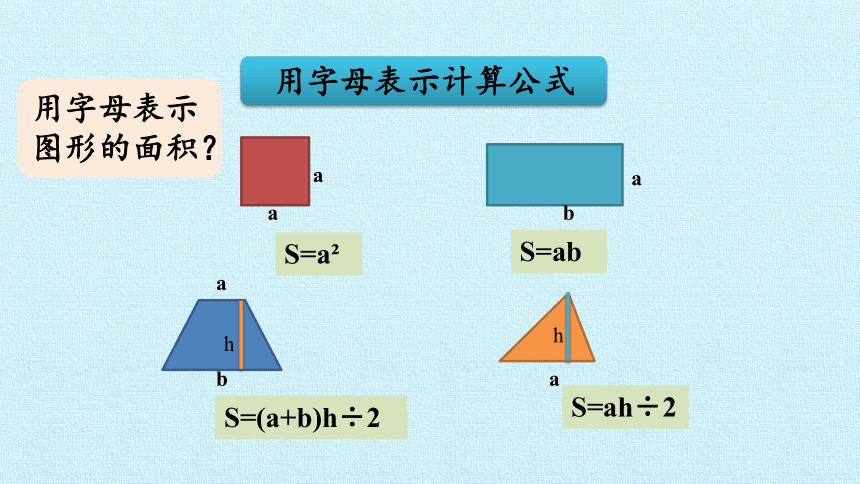
用字母表示计算公式
a
a
a
b
a
h
a
b
h
用字母表示图形的面积?
S=a
S=ab
S=(a+b)h÷2
S=ah÷2
在含有字母的式子里,数字和字母中间的乘号可以记作小圆点,也可以省略不写。在省略乘号时,要把数字写在字母的前面。如:b×3=3·b或3b
数与字母相乘可以怎样简写?
字母与1相乘可以怎样简写?
任何字母与1相乘,1都可以省略不写。如:1×a=a或a×1=a
字母与字母相乘可以怎样简写?两个相同字母怎么办?
字母与字母相乘,中间的乘号可以记作小圆点,也可以省略不写。如:a×b=a·b或ab。
两个相同的字母相乘,如m×m=m ,读作m的平方。
说出下面每个式子表示的意义。
老师家上月用水a吨,本月用水比上月节约b吨。
(1)a-b表示什么?
(2)2a-b表示什么?
a-b表示老师家本月用水的吨数。
2a-b表示老师家上月和本月一共用水的吨数。
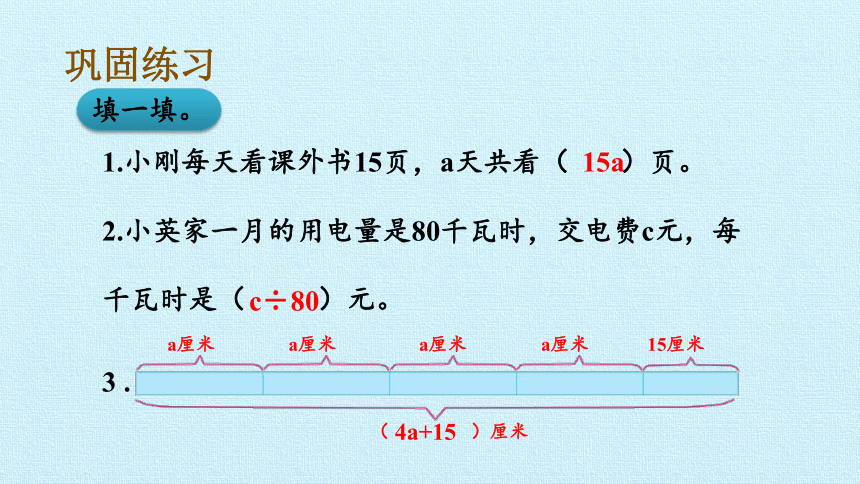
巩固练习
填一填。
1.小刚每天看课外书15页,a天共看( )页。
2.小英家一月的用电量是80千瓦时,交电费c元,每
千瓦时是( )元。
a厘米
a厘米
a厘米
a厘米
15厘米
( )厘米
3 .
15a
c÷80
4a+15
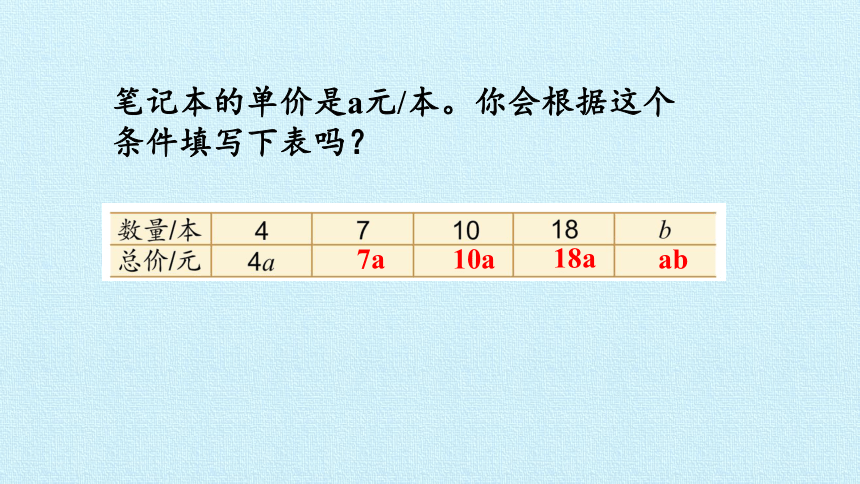
笔记本的单价是a元/本。你会根据这个条件填写下表吗?
7a
10a
18a
ab
用式子表示下面的数量关系。
1. 5和9的积减去x的3倍的差。
2. b的4.5倍与a的和。
3. x与1.5的积加上8.2的和。
5×9-3x
4.5b+a
1.5x+8.2
数字与数字相乘不能省略乘号。
省略乘号,写出下面各式。
4×c= x×5=
1×m= b×b=
a×c= n×6=
4c
m
ac
5x
b
6n
在括号里填写含有字母的式子。
(1)小玲买了1支钢笔和4个笔记本,每支钢笔7元,每个笔记本a元,她一共付出( )元。
(2)食堂运进a袋大米,每袋50千克,已经吃掉x千克。还剩( )千克。
(3)买6面小鼓用去a元,买1面大鼓用去b元。1面小鼓比1面大鼓便宜( )元。
7+4a
50a-x
b-a÷6
说说下面每个式子表示的意义。
(1)育才小学五年级同学植树78棵,六年级比五年级多植x棵。78+x表示什么?
(2)学校买来9个足球,单价是a元/个;又买来b个篮球,单价是25元/个。9a和25b各表示什么?9+b和9a+25b呢?
答:9a表示9个足球的价钱,25b表示25个篮球的价钱。9+b表示足球和篮球的总个数。9a+25b表示9个足球和25个篮球合计的价钱。
答:78+x表示六年级植树的棵数。
∠3=(180°-a°)÷2
用含字母的式子表示每个三角形中∠3的度数。
(1)∠1=a°,∠2=b°。
(2)∠1=a°,∠2=a°。
(3)∠1=a°,∠2和∠3相等。
∠3=180°-a°-b°
∠3=180°-2a°
S=ah
=5×2.4
=12
C=4a
=4×12
=48
答:正方形的周长是48分米,面积是144平方分米。
S=a
=12×12
=144
C=2(a+b)
=2×(15+8)
=46
答:长方形的周长是46米,面积是120平方米。
S=ab
=15×8
=120
先写出公式,再把数值代入公式计算。
(1)一个平行四边形,底5cm,高2.4cm。求它的面积。
答:它的面积是12平方厘米。
(2)一个正方形的边长是12dm,求它的周长和面积。
(3)求长15m,宽8m的长方形的周长和面积。
S=vt
=80×3.5
=280
答:这辆汽车3.5小时行驶的路程是280千米。
用s表示路程,v表示速度,t表示时间。
(1)求路程的公式可以写成:S=
(2)一辆汽车的速度是80千米/时,利用上面的公式求出汽车3.5小时行驶的路程。
vt
先找出下表中每行数的排列规律,再用含有字母的式子填空。
1 2 3 4 5 … n …
2 4 6 8 10 … …
1 3 5 7 9 … …
2n
2n-1
你们都学会了哪些知识?
1.用含有字母的式子不仅可以表示数量关系,还可以表示数量。
2.在含有字母的式子里,数字和字母或字母与字母中间的乘号可以记作小圆点,也可以省略不写。在省略乘号时,要把数字写在字母的前面。
课堂小结
复习旧知
用含有字母的式子表示数量关系和计算公式
a
b
长方形的周长=(长+宽)×2
C=(a+b)×2
省略乘号:C=2(a+b)
如a表示单价,b表示数量,c表示总价。
(1)已知单价、数量,求总价。
(2)已知总价、数量,求单价。
(3)已知单价、总价,求数量。
c=ab
b=c÷a
a=c÷b
如:
用字母表示运算律
加法交换律:a+b=b+a
加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:a×b×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c
用含字母的式子表示数量
(1)搭一个正方形要用4根小棒,搭n个正方形要( )根小棒。
(2)一件衣服用布2米,x米布可做衣服( )件。
(3)一个正方形花坛长5米,四周有一条a米宽的小路。小路的面积( )平方米,小路外边一圈的周长( )米。
4n
x÷2
4a (5+a)
20+8a
3.两个相同的字母相乘时,通常也应采用简便写法。如a×a既可以写成a·a,也可以写成a2,读作a的平方。
1.在含有字母的式子里,式子中间的乘号可以记作“·”,也可省略不写。如:α×2可以写成2·α或者2α。
2.在省略乘号的时候,要把数写在字母的前面。a与1相乘,一般写作 a。如:α×1或1×α可以写成α。
含有字母式子的书写
把数带入含有字母的式子的基本格式是怎样的?
(1)先写出用字母表示的简写算式。
(2)写完“当……时”后,再写出简写算式,然后用数字代替字母,还原乘号,算出结果。
(3)不写单位,要写答语。
把数带入含有字母的式子求值
例:煤气公司铺设一段管道,3米长的钢管用了x根,5米长的钢管用了y根。
(1)用式子表示这段管道的长度。
(2)当x=40根,y=30根时,这段管道长多少米?
3x+5y
当x=40,y=30时
3x+5y=3×40+5×30
=120+150
=270
答:这段管道长270米。
化简含有字母的式子
化简形如“ax±bx”的式子,可以运用乘法分配律进行化简。
计算下面各题。
3x+5x= 10y-9y= 15a+10a=
1×a= 6a-a= y×y=
8x
y
5a
a
y
25a
巩固练习
计算下面各题。
4x+5x= 3b+b=
4a-a= 8x-7x=
9x
4b
3a
x
明明从家出发,每分钟行65米,a分钟可到学校;冬冬从家出发,每分钟行75米,a分钟也可到学校。从明明家到冬冬家一共有( )米。
140a
同学们采集植物标本,四年级采集了a个,六年级采集的个数是四年级的3倍,两个年级一共采集了( )个,四年级比六年级少采集( )个。
4a
2a
根据运算律,在 里填上合适的数或字母。
3.6+(a+6.4)=( + )+a
4·a·25=( · )·a
3x+2x=( + )×
3.6
6.4
4
25
3
2
x
表示3个文具盒的价钱
表示1个文具盒和1副三角板的价钱
表示1个文具盒和2副三角板的价钱
(1)说出下面每个式子表示的意义。
3a a+b a+2b
a元/个
b元/副
3a a+b a+2b
(2)如果a=8,b=4,求上面各式的值。
当a=8,b=4时
3a=3×8
=24
a+b=8+4
=12
a+2b=8+2×4
=8+8
=16
S=ah÷2
=28×16÷2
=448÷2
=224
S=ah
=11×8
=88
S=(a+b)h÷2
=(5+7)×6÷2
=12×6÷2
=72÷2
=36
应用面积公式计算个图形的面积。
3000-5x=3000-5×400
=3000-2000
=1000
答:还剩1000米没有铺。
铺设一条长3千米的自来水管道,已经铺了5天,每天铺x米。先用含字母的式子表示还没铺的米数,再计算当x=400时,还剩多少米没铺?
5a+6a=11a
11a=11×4
=44
答:这天一共运土44吨。
一个工地用汽车运土,每辆车运a吨。一天上午运了5车,下午运了6车。先用含有字母的式子表示这天一共运土的吨数,再计算当a=4时,这天应该运土多少吨。
当a=4时
王伯伯家有一片果园,如下图。
(1)王伯伯家苹果园和梨园的面积相差多少平方米?
苹果园
梨园
30米
8米
a米
30a-8a=(30-8)a=22a
王伯伯家有一片果园,如下图。
苹果园
梨园
30米
8米
a米
(2)如果要在苹果园四周插上篱笆,当a=13时,篱笆长多少米?
当a=13时
60+2a=60+2×13
=60+26
=86
答:篱笆长86米。
你们都学会了哪些知识?
1.用含有字母的式子不仅可以表示数量关系,还可以表示数量和计算公式。
2.在含有字母的式子里,数字和字母或字母与字母中间的乘号可以记作小圆点,也可以省略不写。在省略乘号时,要把数字写在字母的前面。
课堂小结
你们都学会了哪些知识?
课堂小结
用字母表示运算律:
加法交换律:a+b=b+a
加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:a×b×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c
达标检测
1.小南今年a岁,爸爸今年32岁,6年后,爸爸比小南大( )岁。
2.y×5和5×y通常可以写成( );y×y可以写成yy,也可以写成( ),读作( );如果y和1相乘,就可以直接写成( )。
3.5台烤箱的总价是a元,每台烤箱是( )元。
4.山羊有a只,比绵羊多5只,则绵羊有( )只,一共有( )只羊。
5.妈妈去超市买了2瓶洗衣液和4块肥皂,每瓶洗衣液45元,每块肥皂g元,妈妈一共要付( )元。
6.周一升旗仪式,五年级一班同学站了5行,每行有男生a人,女生有b人,五年级一班有( )人。
32-a
5y
y2
y的平方
y
5
a
a-5
2a-5
90+4g
5(a+b)
谢 谢
八 用字母表示数
复习课件
用字母表示数
用含字母的式子表示简单的数量关系
用含字母的式子表示较复杂的数量关系
化简含有字母的式子
复习旧知
字母可以表示确定的数
K表示13
J表示11
2 4 6 m 10 12
m=
8
n×5=15
n=
3
用字母表示运算律
加法交换律:a+b=b+a
加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:a×b×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c
用含字母的式子表示数量关系
原来有n元
现在有( )元。
车上原来有x人。
现在有( )人。
每袋有a条鱼,共有
( )条鱼。
有m个饺子,每盘装10个,可以装( )盘。
n+3
x-5
3a
m÷10
用字母表示计算公式
a
a
a
b
a
h
a
b
h
用字母表示图形的面积?
S=a
S=ab
S=(a+b)h÷2
S=ah÷2
在含有字母的式子里,数字和字母中间的乘号可以记作小圆点,也可以省略不写。在省略乘号时,要把数字写在字母的前面。如:b×3=3·b或3b
数与字母相乘可以怎样简写?
字母与1相乘可以怎样简写?
任何字母与1相乘,1都可以省略不写。如:1×a=a或a×1=a
字母与字母相乘可以怎样简写?两个相同字母怎么办?
字母与字母相乘,中间的乘号可以记作小圆点,也可以省略不写。如:a×b=a·b或ab。
两个相同的字母相乘,如m×m=m ,读作m的平方。
说出下面每个式子表示的意义。
老师家上月用水a吨,本月用水比上月节约b吨。
(1)a-b表示什么?
(2)2a-b表示什么?
a-b表示老师家本月用水的吨数。
2a-b表示老师家上月和本月一共用水的吨数。
巩固练习
填一填。
1.小刚每天看课外书15页,a天共看( )页。
2.小英家一月的用电量是80千瓦时,交电费c元,每
千瓦时是( )元。
a厘米
a厘米
a厘米
a厘米
15厘米
( )厘米
3 .
15a
c÷80
4a+15
笔记本的单价是a元/本。你会根据这个条件填写下表吗?
7a
10a
18a
ab
用式子表示下面的数量关系。
1. 5和9的积减去x的3倍的差。
2. b的4.5倍与a的和。
3. x与1.5的积加上8.2的和。
5×9-3x
4.5b+a
1.5x+8.2
数字与数字相乘不能省略乘号。
省略乘号,写出下面各式。
4×c= x×5=
1×m= b×b=
a×c= n×6=
4c
m
ac
5x
b
6n
在括号里填写含有字母的式子。
(1)小玲买了1支钢笔和4个笔记本,每支钢笔7元,每个笔记本a元,她一共付出( )元。
(2)食堂运进a袋大米,每袋50千克,已经吃掉x千克。还剩( )千克。
(3)买6面小鼓用去a元,买1面大鼓用去b元。1面小鼓比1面大鼓便宜( )元。
7+4a
50a-x
b-a÷6
说说下面每个式子表示的意义。
(1)育才小学五年级同学植树78棵,六年级比五年级多植x棵。78+x表示什么?
(2)学校买来9个足球,单价是a元/个;又买来b个篮球,单价是25元/个。9a和25b各表示什么?9+b和9a+25b呢?
答:9a表示9个足球的价钱,25b表示25个篮球的价钱。9+b表示足球和篮球的总个数。9a+25b表示9个足球和25个篮球合计的价钱。
答:78+x表示六年级植树的棵数。
∠3=(180°-a°)÷2
用含字母的式子表示每个三角形中∠3的度数。
(1)∠1=a°,∠2=b°。
(2)∠1=a°,∠2=a°。
(3)∠1=a°,∠2和∠3相等。
∠3=180°-a°-b°
∠3=180°-2a°
S=ah
=5×2.4
=12
C=4a
=4×12
=48
答:正方形的周长是48分米,面积是144平方分米。
S=a
=12×12
=144
C=2(a+b)
=2×(15+8)
=46
答:长方形的周长是46米,面积是120平方米。
S=ab
=15×8
=120
先写出公式,再把数值代入公式计算。
(1)一个平行四边形,底5cm,高2.4cm。求它的面积。
答:它的面积是12平方厘米。
(2)一个正方形的边长是12dm,求它的周长和面积。
(3)求长15m,宽8m的长方形的周长和面积。
S=vt
=80×3.5
=280
答:这辆汽车3.5小时行驶的路程是280千米。
用s表示路程,v表示速度,t表示时间。
(1)求路程的公式可以写成:S=
(2)一辆汽车的速度是80千米/时,利用上面的公式求出汽车3.5小时行驶的路程。
vt
先找出下表中每行数的排列规律,再用含有字母的式子填空。
1 2 3 4 5 … n …
2 4 6 8 10 … …
1 3 5 7 9 … …
2n
2n-1
你们都学会了哪些知识?
1.用含有字母的式子不仅可以表示数量关系,还可以表示数量。
2.在含有字母的式子里,数字和字母或字母与字母中间的乘号可以记作小圆点,也可以省略不写。在省略乘号时,要把数字写在字母的前面。
课堂小结
复习旧知
用含有字母的式子表示数量关系和计算公式
a
b
长方形的周长=(长+宽)×2
C=(a+b)×2
省略乘号:C=2(a+b)
如a表示单价,b表示数量,c表示总价。
(1)已知单价、数量,求总价。
(2)已知总价、数量,求单价。
(3)已知单价、总价,求数量。
c=ab
b=c÷a
a=c÷b
如:
用字母表示运算律
加法交换律:a+b=b+a
加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:a×b×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c
用含字母的式子表示数量
(1)搭一个正方形要用4根小棒,搭n个正方形要( )根小棒。
(2)一件衣服用布2米,x米布可做衣服( )件。
(3)一个正方形花坛长5米,四周有一条a米宽的小路。小路的面积( )平方米,小路外边一圈的周长( )米。
4n
x÷2
4a (5+a)
20+8a
3.两个相同的字母相乘时,通常也应采用简便写法。如a×a既可以写成a·a,也可以写成a2,读作a的平方。
1.在含有字母的式子里,式子中间的乘号可以记作“·”,也可省略不写。如:α×2可以写成2·α或者2α。
2.在省略乘号的时候,要把数写在字母的前面。a与1相乘,一般写作 a。如:α×1或1×α可以写成α。
含有字母式子的书写
把数带入含有字母的式子的基本格式是怎样的?
(1)先写出用字母表示的简写算式。
(2)写完“当……时”后,再写出简写算式,然后用数字代替字母,还原乘号,算出结果。
(3)不写单位,要写答语。
把数带入含有字母的式子求值
例:煤气公司铺设一段管道,3米长的钢管用了x根,5米长的钢管用了y根。
(1)用式子表示这段管道的长度。
(2)当x=40根,y=30根时,这段管道长多少米?
3x+5y
当x=40,y=30时
3x+5y=3×40+5×30
=120+150
=270
答:这段管道长270米。
化简含有字母的式子
化简形如“ax±bx”的式子,可以运用乘法分配律进行化简。
计算下面各题。
3x+5x= 10y-9y= 15a+10a=
1×a= 6a-a= y×y=
8x
y
5a
a
y
25a
巩固练习
计算下面各题。
4x+5x= 3b+b=
4a-a= 8x-7x=
9x
4b
3a
x
明明从家出发,每分钟行65米,a分钟可到学校;冬冬从家出发,每分钟行75米,a分钟也可到学校。从明明家到冬冬家一共有( )米。
140a
同学们采集植物标本,四年级采集了a个,六年级采集的个数是四年级的3倍,两个年级一共采集了( )个,四年级比六年级少采集( )个。
4a
2a
根据运算律,在 里填上合适的数或字母。
3.6+(a+6.4)=( + )+a
4·a·25=( · )·a
3x+2x=( + )×
3.6
6.4
4
25
3
2
x
表示3个文具盒的价钱
表示1个文具盒和1副三角板的价钱
表示1个文具盒和2副三角板的价钱
(1)说出下面每个式子表示的意义。
3a a+b a+2b
a元/个
b元/副
3a a+b a+2b
(2)如果a=8,b=4,求上面各式的值。
当a=8,b=4时
3a=3×8
=24
a+b=8+4
=12
a+2b=8+2×4
=8+8
=16
S=ah÷2
=28×16÷2
=448÷2
=224
S=ah
=11×8
=88
S=(a+b)h÷2
=(5+7)×6÷2
=12×6÷2
=72÷2
=36
应用面积公式计算个图形的面积。
3000-5x=3000-5×400
=3000-2000
=1000
答:还剩1000米没有铺。
铺设一条长3千米的自来水管道,已经铺了5天,每天铺x米。先用含字母的式子表示还没铺的米数,再计算当x=400时,还剩多少米没铺?
5a+6a=11a
11a=11×4
=44
答:这天一共运土44吨。
一个工地用汽车运土,每辆车运a吨。一天上午运了5车,下午运了6车。先用含有字母的式子表示这天一共运土的吨数,再计算当a=4时,这天应该运土多少吨。
当a=4时
王伯伯家有一片果园,如下图。
(1)王伯伯家苹果园和梨园的面积相差多少平方米?
苹果园
梨园
30米
8米
a米
30a-8a=(30-8)a=22a
王伯伯家有一片果园,如下图。
苹果园
梨园
30米
8米
a米
(2)如果要在苹果园四周插上篱笆,当a=13时,篱笆长多少米?
当a=13时
60+2a=60+2×13
=60+26
=86
答:篱笆长86米。
你们都学会了哪些知识?
1.用含有字母的式子不仅可以表示数量关系,还可以表示数量和计算公式。
2.在含有字母的式子里,数字和字母或字母与字母中间的乘号可以记作小圆点,也可以省略不写。在省略乘号时,要把数字写在字母的前面。
课堂小结
你们都学会了哪些知识?
课堂小结
用字母表示运算律:
加法交换律:a+b=b+a
加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:a×b×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c
达标检测
1.小南今年a岁,爸爸今年32岁,6年后,爸爸比小南大( )岁。
2.y×5和5×y通常可以写成( );y×y可以写成yy,也可以写成( ),读作( );如果y和1相乘,就可以直接写成( )。
3.5台烤箱的总价是a元,每台烤箱是( )元。
4.山羊有a只,比绵羊多5只,则绵羊有( )只,一共有( )只羊。
5.妈妈去超市买了2瓶洗衣液和4块肥皂,每瓶洗衣液45元,每块肥皂g元,妈妈一共要付( )元。
6.周一升旗仪式,五年级一班同学站了5行,每行有男生a人,女生有b人,五年级一班有( )人。
32-a
5y
y2
y的平方
y
5
a
a-5
2a-5
90+4g
5(a+b)
谢 谢
