6.4.1 多边形的内角和与外角和 课件(共21张PPT)
文档属性
| 名称 | 6.4.1 多边形的内角和与外角和 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-13 00:00:00 | ||
图片预览



文档简介
第4节 多边形的内角和与外角和
(第1课时)
第六章 平行四边形
2021年春北师大版八年级数学下册
1 掌握多边形内角和定理,进一步了解转化的数学思想;(重点)
2 经历探索多边形的内角和公式的过程;会应用公式解决问题。(难点)
学习目标
三角形的内角和是多少?
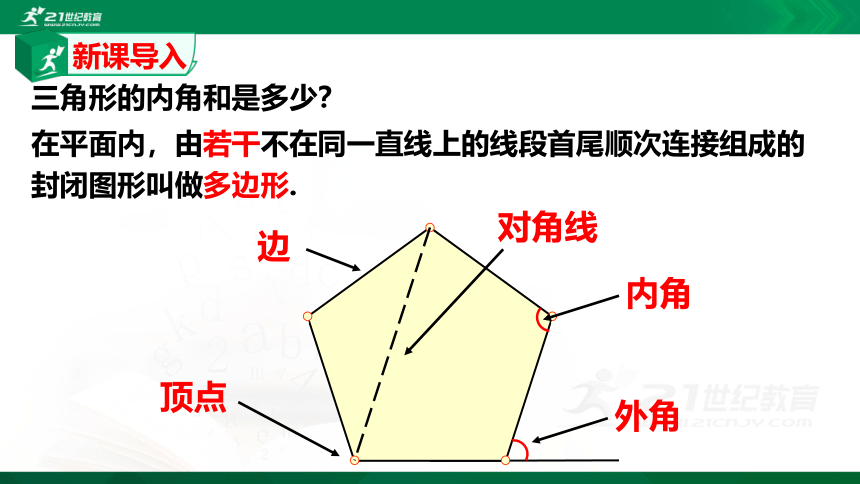
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形.
.
.
.
.
.
顶点
对角线
边
内角
外角
新课导入
多边形的内角和
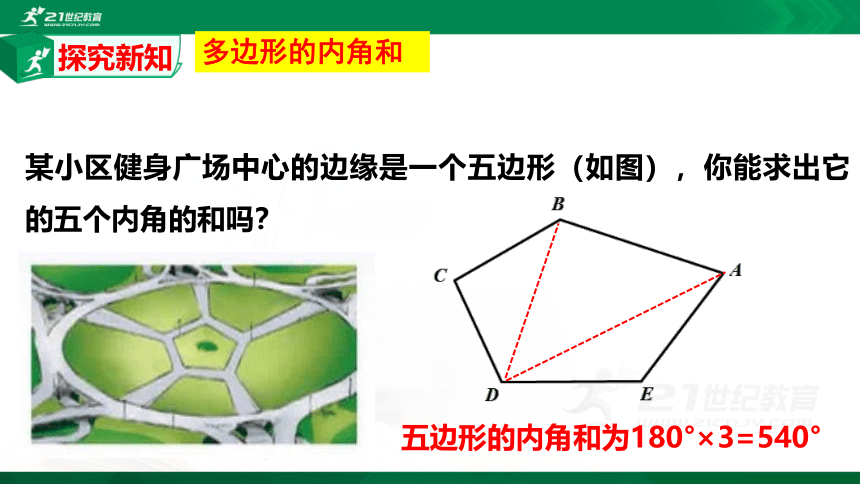
某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗?
五边形的内角和为180°×3=540°
探究新知
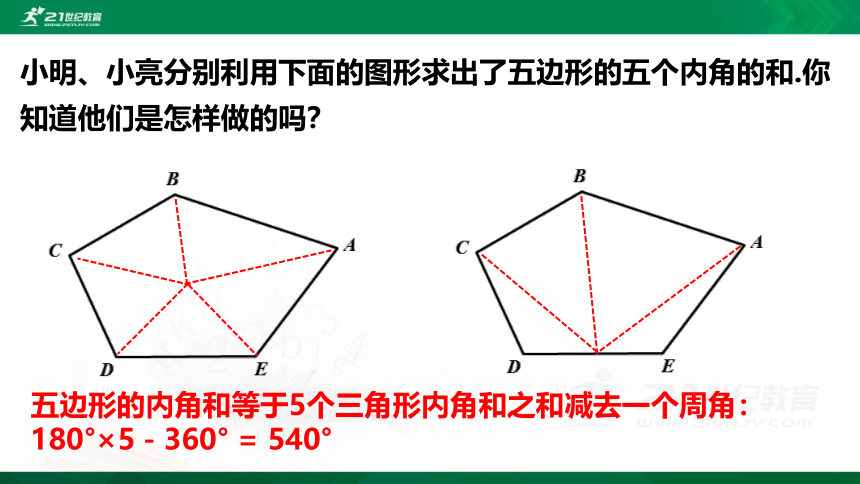
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
五边形的内角和等于5个三角形内角和之和减去一个周角:
180°×5-360° = 540°
想一 想
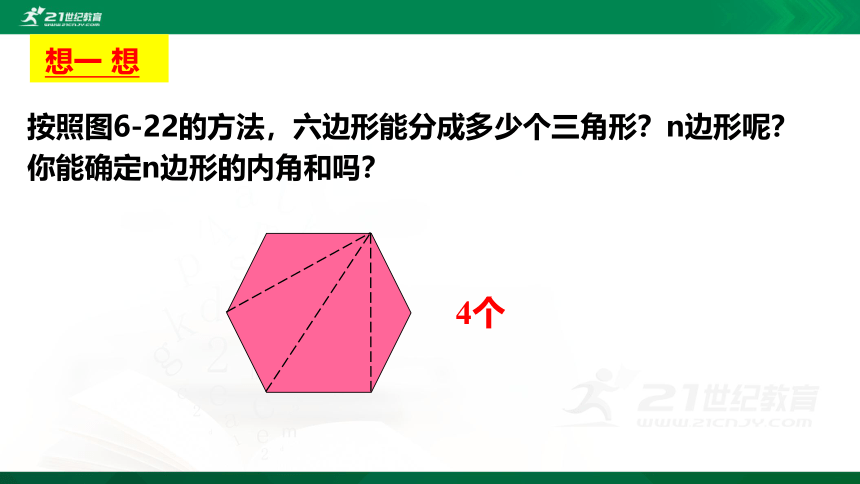
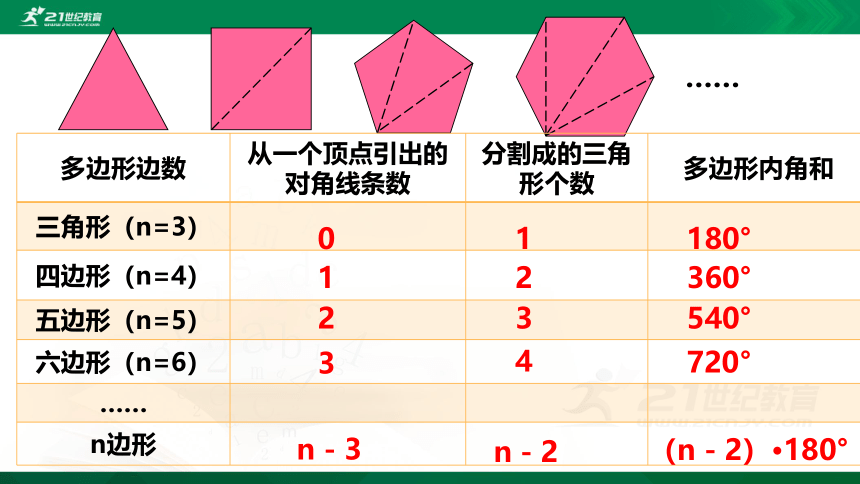
按照图6-22的方法,六边形能分成多少个三角形?n边形呢?你能确定n边形的内角和吗?
4个
……
{ED083AE6-46FA-4A59-8FB0-9F97EB10719F}多边形边数
从一个顶点引出的对角线条数
分割成的三角形个数
多边形内角和
三角形(n=3)
四边形(n=4)
五边形(n=5)
六边形(n=6)
……
n边形
0
1
180°
1
2
360°
2
3
540°
3
4
720°
n-3
n-2
(n-2)·180°
多边形内角和定理:
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2).
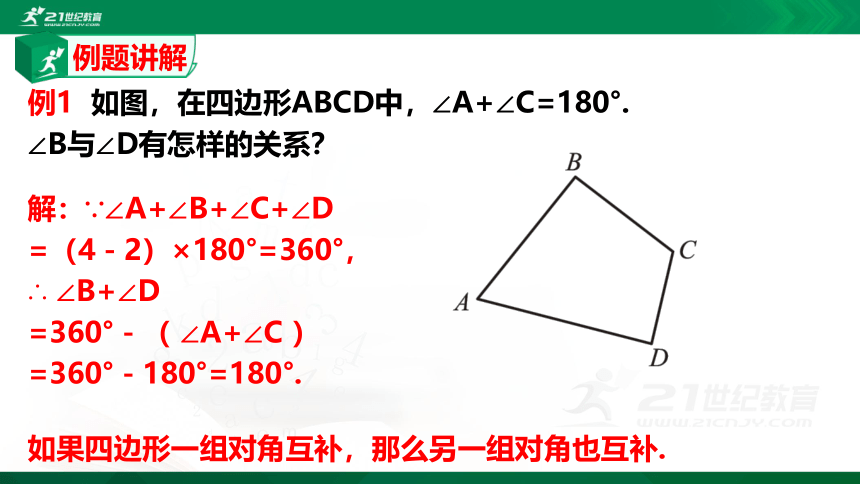
例1 如图,在四边形ABCD中,∠A+∠C=180°.
∠B与∠D有怎样的关系?
解:∵∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴ ∠B+∠D
=360°-( ∠A+∠C )
=360°-180°=180°.
如果四边形一组对角互补,那么另一组对角也互补.
例题讲解
例2 一个多边形的内角和为1440°,则它是几边形?
解:设这个多边形是n边形,则
180°·(n-2)=1440°
∴ n=10
∴ 这个多边形是10边形
例题讲解
想 一 想
正多边形的内角和
正三角形(等边三角形)、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?
探究新知
剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
议 一 议
正n边形的每个内角度数为:
例3 若一个多边形的内角和是1 260°,则这个多边形的边数是_____.
解析:设这个多边形的边数为n,由题意知,
(n-2)×180°=1 260°,解得n=9.
9
例题讲解
1 在四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数是( )
A.80° B.90° C.170° D.20°
课堂练习
2 如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①② B.①③ C.②④ D.③④
3 将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540°
C.720° D.900°
4 一个多边形截去一个角后,形成一个新多边形的内角和是1 620°,则原来多边形的边数是( )
A.10 B.11
C.12 D.以上都有可能
5 小彬求出一个正多边形的一个内角为145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
1 多边形的内角和定理:n边形的内角和等于(n-2)·180°
2 正多边形内角的度数:
课堂小结
谢谢聆听
(第1课时)
第六章 平行四边形
2021年春北师大版八年级数学下册
1 掌握多边形内角和定理,进一步了解转化的数学思想;(重点)
2 经历探索多边形的内角和公式的过程;会应用公式解决问题。(难点)
学习目标
三角形的内角和是多少?
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形.
.
.
.
.
.
顶点
对角线
边
内角
外角
新课导入
多边形的内角和
某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗?
五边形的内角和为180°×3=540°
探究新知
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
五边形的内角和等于5个三角形内角和之和减去一个周角:
180°×5-360° = 540°
想一 想
按照图6-22的方法,六边形能分成多少个三角形?n边形呢?你能确定n边形的内角和吗?
4个
……
{ED083AE6-46FA-4A59-8FB0-9F97EB10719F}多边形边数
从一个顶点引出的对角线条数
分割成的三角形个数
多边形内角和
三角形(n=3)
四边形(n=4)
五边形(n=5)
六边形(n=6)
……
n边形
0
1
180°
1
2
360°
2
3
540°
3
4
720°
n-3
n-2
(n-2)·180°
多边形内角和定理:
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2).
例1 如图,在四边形ABCD中,∠A+∠C=180°.
∠B与∠D有怎样的关系?
解:∵∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴ ∠B+∠D
=360°-( ∠A+∠C )
=360°-180°=180°.
如果四边形一组对角互补,那么另一组对角也互补.
例题讲解
例2 一个多边形的内角和为1440°,则它是几边形?
解:设这个多边形是n边形,则
180°·(n-2)=1440°
∴ n=10
∴ 这个多边形是10边形
例题讲解
想 一 想
正多边形的内角和
正三角形(等边三角形)、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?
探究新知
剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
议 一 议
正n边形的每个内角度数为:
例3 若一个多边形的内角和是1 260°,则这个多边形的边数是_____.
解析:设这个多边形的边数为n,由题意知,
(n-2)×180°=1 260°,解得n=9.
9
例题讲解
1 在四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数是( )
A.80° B.90° C.170° D.20°
课堂练习
2 如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①② B.①③ C.②④ D.③④
3 将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540°
C.720° D.900°
4 一个多边形截去一个角后,形成一个新多边形的内角和是1 620°,则原来多边形的边数是( )
A.10 B.11
C.12 D.以上都有可能
5 小彬求出一个正多边形的一个内角为145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
1 多边形的内角和定理:n边形的内角和等于(n-2)·180°
2 正多边形内角的度数:
课堂小结
谢谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
