等腰梯形与直角梯形 课件
图片预览





文档简介
(共17张PPT)
常见辅助线
性质定理1
性质定理2
应用
旧知复习
等腰梯形
直角梯形
课 题
学习目标
练习1
练习2
小结
作业
复习引入
怎样的四边形是梯形?
常见辅助线
只有一组对边平行
梯形
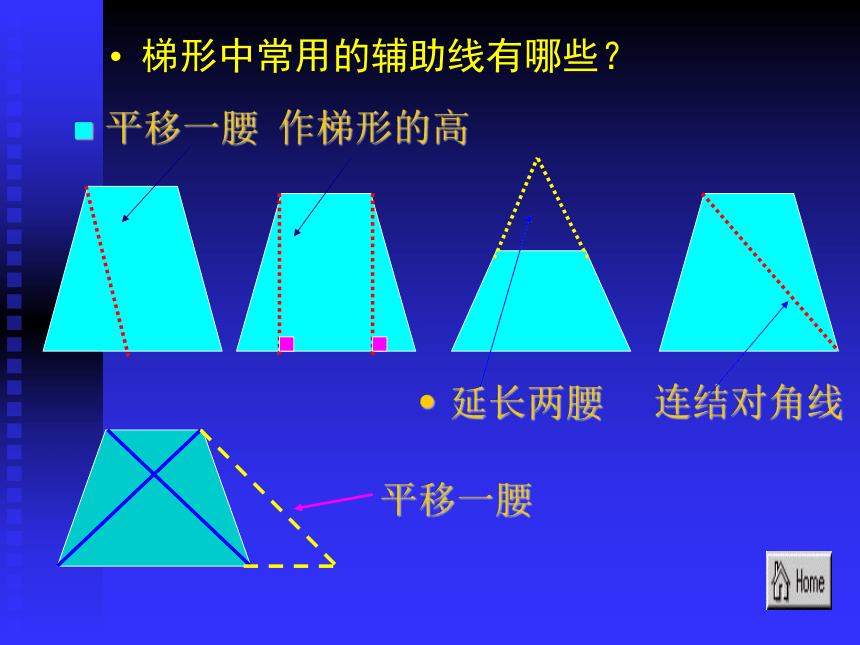
平移一腰 作梯形的高
梯形中常用的辅助线有哪些?
延长两腰 连结对角线
平移一腰
性质定理1巩固练习
1.下列说法中正确的是( )
A.等腰梯形两底角相等
B等腰梯形的一组对边相等且平行
C等腰梯形同一底上的两个角都等于90度
D等腰梯形的四个内角没有一个是直角
D
2.已知等腰梯形的周长25cm,上、下底分别为7cm、8cm,求腰长。
性质定理1巩固练习
3、已知:梯形ABCD中,AD∥BC,AB=CD,欲证明△ABC≌△DCB,需哪些条件?
A
B
C
D
AB=DC
∠ABC=∠DCB
BC=CB
SAS
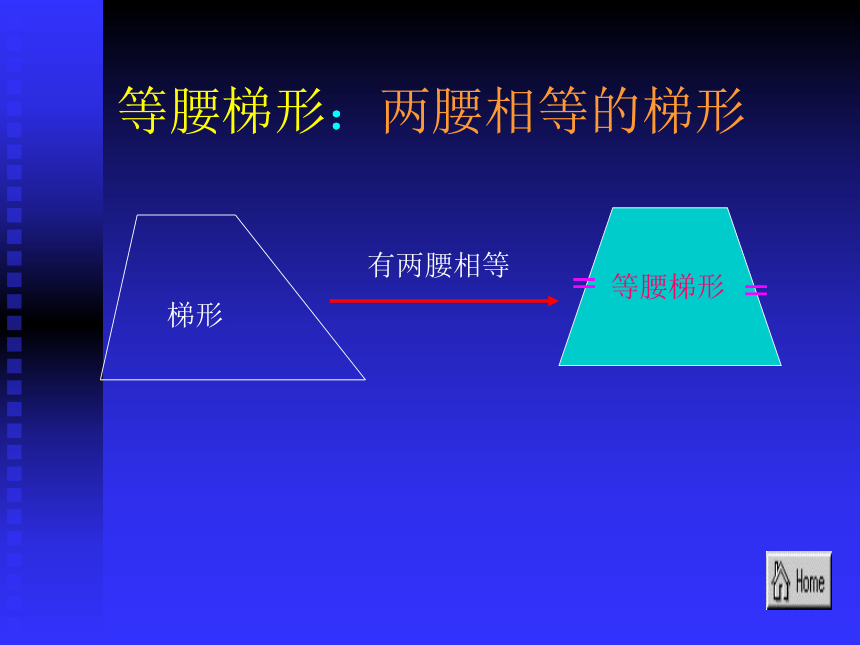
等腰梯形:两腰相等的梯形
有两腰相等
梯形
等腰梯形
直角梯形:
有一个角是直角的梯形。
有一个角是直角
学 习 目 标
1、掌握等腰梯形及直角梯形概念
2、掌握等腰梯形性质定理的证明、运用
A
C
B
D
小组合作讨论:
等腰梯形有哪些特殊性质?
从 边 看:
从 角 看:
两腰相等
同一底上的两个角相等
E
已知:梯形ABCD中,AD∥BC,AB=CD
求证:∠B=∠C
分析:通过添加辅助线,平移一腰,将梯形问题转化为平行四边形和等腰三角形问题来处理。
等腰梯形性质定理1
小组合作探究:
等腰梯形的两条对角线有怎样的关系?
例1 已知:梯形ABCD中,AD∥BC,AB=CD
求证:AC=BD
A
B
C
D
分析:可利用刚学的等腰梯形同一底上的两个角相等,结合全等三角形性质来证明。
等腰梯形性质定理2:
等腰梯形的两条对角线相等。
例2 已知:等腰梯形中的腰和上底相等,且一对角线和一腰垂直,求这个梯形的各个角的大小。
小组讨论、分析:
已知:梯形ABCD中,AD∥BC,AB=CD=AD,BD⊥DC。 求:梯形ABCD的各个角的大小。
A
B
C
D
x
x
x
2x
综合应用:
如图,梯形ABCD中,AD∥BC,∠A=900,∠D=1500,CD=8cm,求AB的长。
A
E
B
D
C
分析:过点D作DE⊥BC,则DE=AB,结合Rt△DCE,求出∠C=300,从而求出DE
本课小结:
本课学习了等腰梯形、直角梯形的概念,直角梯形的性质定理;
通过在梯形中添加适当辅助线,将梯形问题有效地转化为平行四边形及等腰三角形加以解决;
在应用等腰梯形性质定理1时,注意是“同一底上的两个角相等”,不能说成“两底角相等”。
先由学习小组民主小结,再由小组长汇报小结:
布置作业:
1、课堂作业 P36 第3题,P37 第2题。
2、家庭作业《基础训练》P19 第1~3题。
常见辅助线
性质定理1
性质定理2
应用
旧知复习
等腰梯形
直角梯形
课 题
学习目标
练习1
练习2
小结
作业
复习引入
怎样的四边形是梯形?
常见辅助线
只有一组对边平行
梯形
平移一腰 作梯形的高
梯形中常用的辅助线有哪些?
延长两腰 连结对角线
平移一腰
性质定理1巩固练习
1.下列说法中正确的是( )
A.等腰梯形两底角相等
B等腰梯形的一组对边相等且平行
C等腰梯形同一底上的两个角都等于90度
D等腰梯形的四个内角没有一个是直角
D
2.已知等腰梯形的周长25cm,上、下底分别为7cm、8cm,求腰长。
性质定理1巩固练习
3、已知:梯形ABCD中,AD∥BC,AB=CD,欲证明△ABC≌△DCB,需哪些条件?
A
B
C
D
AB=DC
∠ABC=∠DCB
BC=CB
SAS
等腰梯形:两腰相等的梯形
有两腰相等
梯形
等腰梯形
直角梯形:
有一个角是直角的梯形。
有一个角是直角
学 习 目 标
1、掌握等腰梯形及直角梯形概念
2、掌握等腰梯形性质定理的证明、运用
A
C
B
D
小组合作讨论:
等腰梯形有哪些特殊性质?
从 边 看:
从 角 看:
两腰相等
同一底上的两个角相等
E
已知:梯形ABCD中,AD∥BC,AB=CD
求证:∠B=∠C
分析:通过添加辅助线,平移一腰,将梯形问题转化为平行四边形和等腰三角形问题来处理。
等腰梯形性质定理1
小组合作探究:
等腰梯形的两条对角线有怎样的关系?
例1 已知:梯形ABCD中,AD∥BC,AB=CD
求证:AC=BD
A
B
C
D
分析:可利用刚学的等腰梯形同一底上的两个角相等,结合全等三角形性质来证明。
等腰梯形性质定理2:
等腰梯形的两条对角线相等。
例2 已知:等腰梯形中的腰和上底相等,且一对角线和一腰垂直,求这个梯形的各个角的大小。
小组讨论、分析:
已知:梯形ABCD中,AD∥BC,AB=CD=AD,BD⊥DC。 求:梯形ABCD的各个角的大小。
A
B
C
D
x
x
x
2x
综合应用:
如图,梯形ABCD中,AD∥BC,∠A=900,∠D=1500,CD=8cm,求AB的长。
A
E
B
D
C
分析:过点D作DE⊥BC,则DE=AB,结合Rt△DCE,求出∠C=300,从而求出DE
本课小结:
本课学习了等腰梯形、直角梯形的概念,直角梯形的性质定理;
通过在梯形中添加适当辅助线,将梯形问题有效地转化为平行四边形及等腰三角形加以解决;
在应用等腰梯形性质定理1时,注意是“同一底上的两个角相等”,不能说成“两底角相等”。
先由学习小组民主小结,再由小组长汇报小结:
布置作业:
1、课堂作业 P36 第3题,P37 第2题。
2、家庭作业《基础训练》P19 第1~3题。
同课章节目录
