4.3牛顿第二定律瞬时性问题—【新教材】人教版(2019)高中物理必修第一册检测(word含答案)
文档属性
| 名称 | 4.3牛顿第二定律瞬时性问题—【新教材】人教版(2019)高中物理必修第一册检测(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 485.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-14 05:44:26 | ||
图片预览




文档简介
牛顿第二定律瞬时性问题
一、单选题
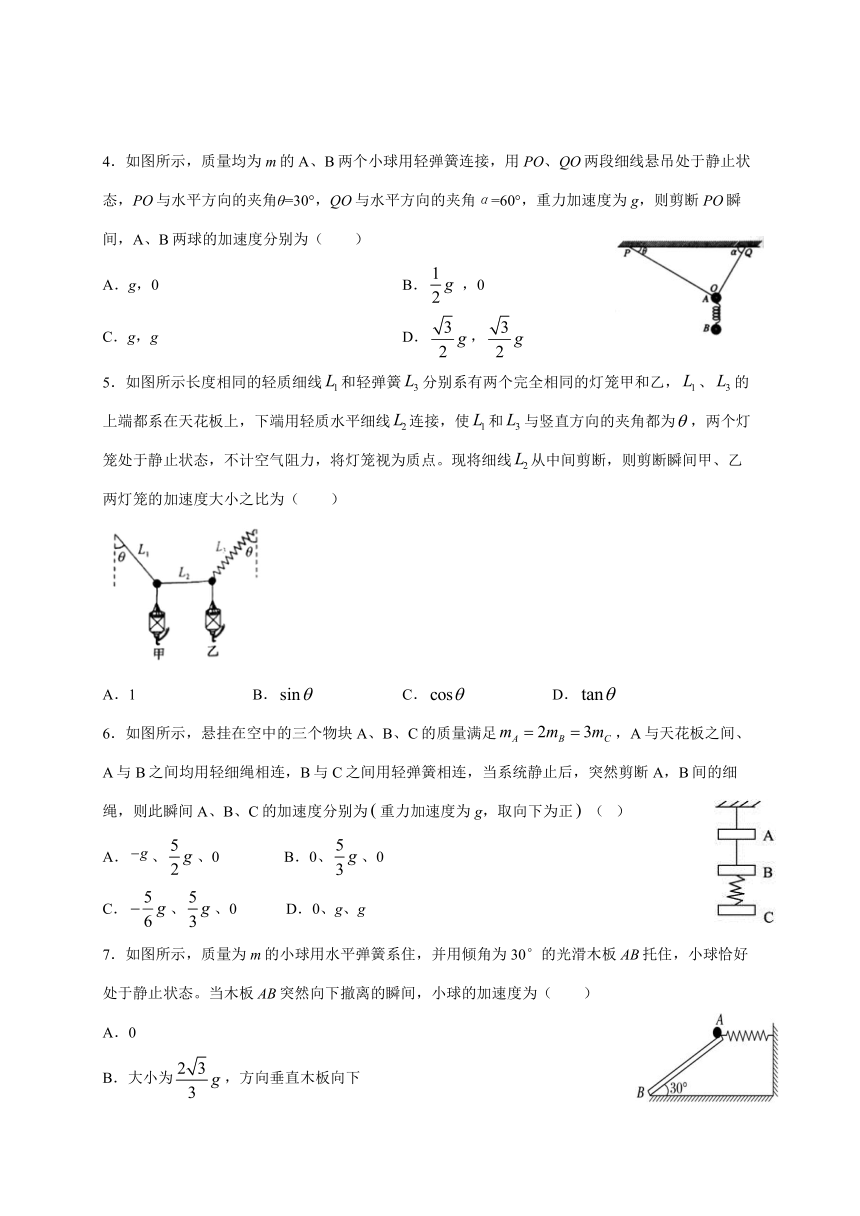
1.如图所示,置于粗糙水平面上的物块A、B用轻质弹簧连接,在水平恒力F的作用下物块A、B以相同的加速度a向右运动,已知物块A的质量是物块B质量的2倍,它们与水平面间的动摩擦因数均为μ,重力加速度为g,现撤去水平恒力F,则在此瞬间( )
A.物块A的加速度大小为0 B.物块B的加速度大小为0
C.物块A的加速度大小为 D.物块B的加速度大小为
2.用细绳拴一个质量为m的小球,小球将一固定在墙上的水平轻质弹簧压缩了x(小球与弹簧不拴连),如图所示。将细绳剪断后( )
A.小球立即获得加速度 B.小球在细绳剪断瞬间起开始做平抛运动
C.小球落地的时间等于 D.小球落地的速度等于
3.如图所示,两个质量分别为m1=2 kg,m2=3 kg的物体置于光滑的水平面上,中间用轻质弹簧测力计连接。两个大小分别为F1=30 N,F2=20 N的水平拉力分别作用在m1,m2上,则( )
A.弹簧测力计的示数是25 N
B.弹簧测力计的示数是50 N
C.在突然撤去力F2的瞬间,m1的加速度大小为5 m/s2
D.在突然撤去力F1的瞬间,m1的加速度大小为13 m/s2
4.如图所示,质量均为m的A、B两个小球用轻弹簧连接,用PO、QO两段细线悬吊处于静止状态,PO与水平方向的夹角θ=30°,QO与水平方向的夹角α=60°,重力加速度为g,则剪断PO瞬间,A、B两球的加速度分别为( )
A.g,0 B. ,0
C.g,g D.,
5.如图所示长度相同的轻质细线和轻弹簧分别系有两个完全相同的灯笼甲和乙,、的上端都系在天花板上,下端用轻质水平细线连接,使和与竖直方向的夹角都为,两个灯笼处于静止状态,不计空气阻力,将灯笼视为质点。现将细线从中间剪断,则剪断瞬间甲、乙两灯笼的加速度大小之比为( )
A.1 B. C. D.
6.如图所示,悬挂在空中的三个物块A、B、C的质量满足,A与天花板之间、A与B之间均用轻细绳相连,B与C之间用轻弹簧相连,当系统静止后,突然剪断A,B间的细绳,则此瞬间A、B、C的加速度分别为重力加速度为g,取向下为正 ( )
A.、、0 B.0、、0
C.、、0 D.0、g、g
7.如图所示,质量为m的小球用水平弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态。当木板AB突然向下撤离的瞬间,小球的加速度为( )
A.0
B.大小为,方向垂直木板向下
C.大小为g,方向竖直向下
D.大小为,方向水平向右
8.如图所示,质量为m的小球被水平绳AO和与竖直方向成角的轻弹簧系着处于静止状态,现将绳AO烧断,在绳AO烧断的瞬间,下列说法正确的是( )(g为重力加速度)
A.小球的加速度
B.小球的加速度
C.小球的加速度为零
D.小球的加速度方向沿弹簧方向
9.细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为,如图所示以下说法正确的是( )
A.小球静止时弹簧的弹力大小为
B.小球静止时细绳的拉力大小为
C.细线烧断瞬间小球的加速度立即为
D.细线烧断瞬间小球的加速度立即为
10.如图所示,倾角为α的斜面固定在水平地面上,斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧相连接,现对A施加一个水平向右大小为F=2mg的恒力,使A、B在斜面上都保持静止,如果斜面和两个小球的摩擦均忽略不计,此时弹簧的长度为L,则下列说法正确的是( )
A.弹簧的原长为
B.斜面的倾角为α=60°
C.撤掉恒力F的瞬间小球A的加速度为
D.撤掉恒力F的瞬间小球B的加速度为零
11.质量均为m的物块ab之间用竖直轻弹簧相连,系在a上的细线竖直悬挂于固定点O,a、b 竖直粗糙墙壁接触,整个系统处于静止状态.重力加速度大小为g,则( )
A.物块b可能受3个力
B.细线中的拉力小于2 mg
C.剪断细线瞬间b的加速度大小为g
D.剪断细线瞬间a的加速度大小为2g
二、多选题
12.如图所示,物体a、b用一根不可伸长的轻细绳相连,再用一根轻弹簧和a相连,弹簧上端固定在天花板上,已知物体a、b的质量相等,重力加速度为g。当在P点剪断绳子的瞬间,下列说法正确的是( )
A.物体a的加速度大小为零
B.物体b的加速度大小为零
C.物体b的加速度大小为g
D.物体b的加速度与物体a的加速度大小相等
13.如图所示,天花板上悬挂一轻质弹簧,弹簧下端栓接质量为m的小球A,A球通过轻杆连接质量为的小球B,重力加速度为g,下列说法正确的是( )
A.剪断弹簧瞬间,轻杆上弹力不为0
B.剪断弹簧瞬间,A、B球加速度均为g
C.剪断轻杆瞬间,A、B球加速度大小均为g
D.剪断轻杆瞬间,A球加速度大小为,B球加速度大小为g
14.如图所示,在动摩擦因数μ=0.2的水平面上有一个质量m=1kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,此时小球处于静止状态,且水平面对小球的弹力恰好为零。在剪断轻绳的瞬间(g取10m/s2,最大静摩擦力等于滑动摩擦力)。下列说法中正确的是( )
A.弹簧的弹力不变
B.小球立即获得向左的加速度,且a=8m/s2
C.小球立即获得向左的加速度,且a=10m/s2
D.若剪断的是弹簧,则剪断瞬间小球加速度的大小a=10m/s2
参考答案
1.C
设AB的质量分别为2m和m,撤去F之前, 对物体B
解得
撤去F的瞬间,弹簧的弹力不变,则B的加速度不变,仍为a;
A受到的合力为
则A的加速度
故选C。
2.C
A.细绳剪断前小球受重力、弹力和拉力的作用,处于平衡状态,故弹力和重力的合力为
F合=
剪断细线瞬间,弹力和重力不变,则两力的合力不变,根据牛顿第二定律有
F合==ma
解得
A错误;
B.平抛运动只受重力;将细绳烧断后,小球受到球的重力和弹簧的弹力的共同的作用,合力斜向右下方,并不是只有重力的作用,所以不是平抛运动,B错误;
C.小球竖直方向只受重力,竖直分运动是自由落体运动,根据自由落体运动规律有
故小球落地的时间
选项C正确;
D.如果不受弹簧弹力,小球做自由落体运动,根据自由落体运动规律有
解得落地速度
由于水平方向有弹簧弹力作用,则水平方向会加速,从而获得水平速度,而竖直方向的速度不变,所以落地速度大于,D错误。
故选C。
3.D
AB.将两个物体与弹簧测力计整体作为研究对象,由牛顿第二定律,有
代入数据,解得,设弹簧测力计读数为F,将m2作为研究对象,有
代入数据,解得,故AB错误;
C.在突然撤去力F2的瞬间,弹簧弹力未变,因此m1的受力情况未变,所以m1的加速度大小仍为2 m/s2,故C错误;
D.在突然撤去力F1的瞬间,m1只受弹簧弹力,因此其加速度大小为
故D正确。
故选D。
4.A
剪断PO的一瞬间,弹簧的弹力不变,因此B的合力为零,加速度为零;
对A研究,剪断PO一瞬间,A受到的合力垂直于QO斜向右下
解得
故A正确,BCD错误,
故选A。
5.C
细线被剪断的瞬间,因细线对甲的弹力突然消失,而引起上的张力发生突变,使甲的受力情况改变,瞬时加速度垂直斜向下方,大小为,方向垂直于斜向下方;当细线被剪断时,细线对乙的弹力突然消失,而弹簧的形变还来不及变化(变化要有一个过程,不能突变),因而弹簧的弹力不变,它与重力的合力与细线对乙的弹力是一对平衡力,等大反向,所以细线被剪断的瞬间,乙加速度的大小为,方向水平向右。甲乙两图中小球的加速度大小之比为
故选C。
6.B
剪断细绳的瞬间,细绳的张力立即消失,上面细绳的张力可突变,则A所受的上面细绳的拉力与重力重新平衡,A的加速度为0。
剪断绳子前,弹簧的弹力为
剪断绳子的瞬间,弹簧的弹力不变,隔离对C分析,合力为零,加速度为
对B分析,根据牛顿第二定律有,加速度为
故选B。
7.B
木板撤去前,小球处于平衡态,受重力、支持力和弹簧的拉力,如图
根据共点力平衡条件,有
代入数据解得
,
木板AB突然撤去后,支持力消失,重力和拉力不变,合力大小等于支持力N,方向与N反向,故加速度为
方向垂直于木板向下,故B正确错误,ACD。
故选B。
8.A
根据平衡状态受力分析可知,绳子拉力
烧断瞬间,弹簧弹力不变,弹簧和重力合力与绳子拉力大小相等,方向相反,所以
方向水平向右,故BCD错误,A正确。
故选A。
9.C
AB.小球静止时,分析受力情况,如图所示
由平衡条件得弹簧的弹力大小为
细绳的拉力大小为
故AB错误;
CD.细绳烧断瞬间弹簧的弹力不变,则小球所受的合力与烧断前细绳拉力的大小相等、方向相反,则此瞬间小球的加速度大小为
故C正确,D错误。
故选C。
10.D
AB.对A、B整体分析,沿斜面方向根据平衡条件可得
Fcosα=2mgsinα
解得
α=45°
对小球B进行受力分析,沿斜面方向由平衡条件可得
kx=mgsinα
解得
所以弹簧的原长为
故AB错误;
C.撤掉恒力F的瞬间,对A进行受力分析,沿斜面方向根据牛顿第二定律可得
mgsinα+kx=maA
小球A此时的加速度,故C错误;
D.撤掉恒力F的瞬间,弹簧弹力不变,B球所受合力不变,故B球的加速度为零,故D正确。
故选D。
11.D
对ab整体分析可知,整体受重力和绳子上的拉力,水平方向如果受墙的弹力,则整体不可能竖直静止,故不会受到水平方向上的弹力,根据平衡条件可知,细线上的拉力F=2mg;再对b分析可知,b只受重力和弹簧拉力而保持静止,故AB错误;由于b处于平衡,故弹簧的拉力F=mg,剪断细线瞬间弹簧的弹力不变,则对b分析可知,b受力不变,合力为零,故加速度为零,故C错误;对a分析可知,剪断细线瞬间a受重力和弹簧向下的拉力,合力Fa=2mg,则由牛顿第二定律可知,加速度为2g,故D正确.故选D.
12.CD
A.设a、b物体的质量为m,剪断细线前,对a、b整体受力分析,受到总重力和弹簧的弹力而平衡,故
再对物体a受力分析,受到重力、细线拉力和弹簧的拉力,剪断细线后,重力和弹簧的弹力不变,细线的拉力减为零,故物体a受到的力的合力等于mg,向上,根据牛顿第二定律得a的加速度为
方向向上,故A错误;
BCD.对物体b受力分析,受到重力、细线拉力,剪断细线后,重力不变,细线的拉力减为零,故物体b受到的力的合力等于mg,向下,根据牛顿第二定律得b的加速度为
方向向下,所以物体a的加速度与物体b的加速度大小相同,故B错误CD正确。
故选CD。
13.BD
AB.剪短弹簧瞬间,以A、B以及杆整体作为研究对象,整体做自由落体运动,加速度为;再隔离B,根据牛顿第二定律可知,小球B做自由落体运动,杆对B的力必须为零,故A错误,B正确;
CD.剪断轻杆瞬间, B球加速度大小为g,做自由落体运动;为剪短轻杆前对A进行受力分析如下
根据平衡条件有
当剪短轻杆后,对球A,除了杆的力消失意外,其他力没有发生变化,根据牛顿第二定律有
得
加速度方向竖直向上,故C错误,D正确。
故选BD。
14.AB
A.剪断轻绳瞬间,弹簧的形变还来不及恢复,即弹簧弹力不会突变,故A正确;
BC.剪断轻绳前,水平面对小球的弹力恰好为零,小球受重力、弹簧的弹力和细线的拉力作用处于平衡,对小球作受力分析,根据平衡条件和几何关系可知,弹簧弹力与小球重力大小相等,即
F=G=mg=10N
剪断轻绳的瞬间,地面对小球的滑动摩擦力为
Ff=μFN=μmg=2N
小球加速度
故B正确,C错误;
D.若剪断弹簧,轻绳对小球的拉力瞬间为零,此时小球所受的合力为零,则小球的加速度为零,故D错误。
故选AB。
一、单选题
1.如图所示,置于粗糙水平面上的物块A、B用轻质弹簧连接,在水平恒力F的作用下物块A、B以相同的加速度a向右运动,已知物块A的质量是物块B质量的2倍,它们与水平面间的动摩擦因数均为μ,重力加速度为g,现撤去水平恒力F,则在此瞬间( )
A.物块A的加速度大小为0 B.物块B的加速度大小为0
C.物块A的加速度大小为 D.物块B的加速度大小为
2.用细绳拴一个质量为m的小球,小球将一固定在墙上的水平轻质弹簧压缩了x(小球与弹簧不拴连),如图所示。将细绳剪断后( )
A.小球立即获得加速度 B.小球在细绳剪断瞬间起开始做平抛运动
C.小球落地的时间等于 D.小球落地的速度等于
3.如图所示,两个质量分别为m1=2 kg,m2=3 kg的物体置于光滑的水平面上,中间用轻质弹簧测力计连接。两个大小分别为F1=30 N,F2=20 N的水平拉力分别作用在m1,m2上,则( )
A.弹簧测力计的示数是25 N
B.弹簧测力计的示数是50 N
C.在突然撤去力F2的瞬间,m1的加速度大小为5 m/s2
D.在突然撤去力F1的瞬间,m1的加速度大小为13 m/s2
4.如图所示,质量均为m的A、B两个小球用轻弹簧连接,用PO、QO两段细线悬吊处于静止状态,PO与水平方向的夹角θ=30°,QO与水平方向的夹角α=60°,重力加速度为g,则剪断PO瞬间,A、B两球的加速度分别为( )
A.g,0 B. ,0
C.g,g D.,
5.如图所示长度相同的轻质细线和轻弹簧分别系有两个完全相同的灯笼甲和乙,、的上端都系在天花板上,下端用轻质水平细线连接,使和与竖直方向的夹角都为,两个灯笼处于静止状态,不计空气阻力,将灯笼视为质点。现将细线从中间剪断,则剪断瞬间甲、乙两灯笼的加速度大小之比为( )
A.1 B. C. D.
6.如图所示,悬挂在空中的三个物块A、B、C的质量满足,A与天花板之间、A与B之间均用轻细绳相连,B与C之间用轻弹簧相连,当系统静止后,突然剪断A,B间的细绳,则此瞬间A、B、C的加速度分别为重力加速度为g,取向下为正 ( )
A.、、0 B.0、、0
C.、、0 D.0、g、g
7.如图所示,质量为m的小球用水平弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态。当木板AB突然向下撤离的瞬间,小球的加速度为( )
A.0
B.大小为,方向垂直木板向下
C.大小为g,方向竖直向下
D.大小为,方向水平向右
8.如图所示,质量为m的小球被水平绳AO和与竖直方向成角的轻弹簧系着处于静止状态,现将绳AO烧断,在绳AO烧断的瞬间,下列说法正确的是( )(g为重力加速度)
A.小球的加速度
B.小球的加速度
C.小球的加速度为零
D.小球的加速度方向沿弹簧方向
9.细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为,如图所示以下说法正确的是( )
A.小球静止时弹簧的弹力大小为
B.小球静止时细绳的拉力大小为
C.细线烧断瞬间小球的加速度立即为
D.细线烧断瞬间小球的加速度立即为
10.如图所示,倾角为α的斜面固定在水平地面上,斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧相连接,现对A施加一个水平向右大小为F=2mg的恒力,使A、B在斜面上都保持静止,如果斜面和两个小球的摩擦均忽略不计,此时弹簧的长度为L,则下列说法正确的是( )
A.弹簧的原长为
B.斜面的倾角为α=60°
C.撤掉恒力F的瞬间小球A的加速度为
D.撤掉恒力F的瞬间小球B的加速度为零
11.质量均为m的物块ab之间用竖直轻弹簧相连,系在a上的细线竖直悬挂于固定点O,a、b 竖直粗糙墙壁接触,整个系统处于静止状态.重力加速度大小为g,则( )
A.物块b可能受3个力
B.细线中的拉力小于2 mg
C.剪断细线瞬间b的加速度大小为g
D.剪断细线瞬间a的加速度大小为2g
二、多选题
12.如图所示,物体a、b用一根不可伸长的轻细绳相连,再用一根轻弹簧和a相连,弹簧上端固定在天花板上,已知物体a、b的质量相等,重力加速度为g。当在P点剪断绳子的瞬间,下列说法正确的是( )
A.物体a的加速度大小为零
B.物体b的加速度大小为零
C.物体b的加速度大小为g
D.物体b的加速度与物体a的加速度大小相等
13.如图所示,天花板上悬挂一轻质弹簧,弹簧下端栓接质量为m的小球A,A球通过轻杆连接质量为的小球B,重力加速度为g,下列说法正确的是( )
A.剪断弹簧瞬间,轻杆上弹力不为0
B.剪断弹簧瞬间,A、B球加速度均为g
C.剪断轻杆瞬间,A、B球加速度大小均为g
D.剪断轻杆瞬间,A球加速度大小为,B球加速度大小为g
14.如图所示,在动摩擦因数μ=0.2的水平面上有一个质量m=1kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,此时小球处于静止状态,且水平面对小球的弹力恰好为零。在剪断轻绳的瞬间(g取10m/s2,最大静摩擦力等于滑动摩擦力)。下列说法中正确的是( )
A.弹簧的弹力不变
B.小球立即获得向左的加速度,且a=8m/s2
C.小球立即获得向左的加速度,且a=10m/s2
D.若剪断的是弹簧,则剪断瞬间小球加速度的大小a=10m/s2
参考答案
1.C
设AB的质量分别为2m和m,撤去F之前, 对物体B
解得
撤去F的瞬间,弹簧的弹力不变,则B的加速度不变,仍为a;
A受到的合力为
则A的加速度
故选C。
2.C
A.细绳剪断前小球受重力、弹力和拉力的作用,处于平衡状态,故弹力和重力的合力为
F合=
剪断细线瞬间,弹力和重力不变,则两力的合力不变,根据牛顿第二定律有
F合==ma
解得
A错误;
B.平抛运动只受重力;将细绳烧断后,小球受到球的重力和弹簧的弹力的共同的作用,合力斜向右下方,并不是只有重力的作用,所以不是平抛运动,B错误;
C.小球竖直方向只受重力,竖直分运动是自由落体运动,根据自由落体运动规律有
故小球落地的时间
选项C正确;
D.如果不受弹簧弹力,小球做自由落体运动,根据自由落体运动规律有
解得落地速度
由于水平方向有弹簧弹力作用,则水平方向会加速,从而获得水平速度,而竖直方向的速度不变,所以落地速度大于,D错误。
故选C。
3.D
AB.将两个物体与弹簧测力计整体作为研究对象,由牛顿第二定律,有
代入数据,解得,设弹簧测力计读数为F,将m2作为研究对象,有
代入数据,解得,故AB错误;
C.在突然撤去力F2的瞬间,弹簧弹力未变,因此m1的受力情况未变,所以m1的加速度大小仍为2 m/s2,故C错误;
D.在突然撤去力F1的瞬间,m1只受弹簧弹力,因此其加速度大小为
故D正确。
故选D。
4.A
剪断PO的一瞬间,弹簧的弹力不变,因此B的合力为零,加速度为零;
对A研究,剪断PO一瞬间,A受到的合力垂直于QO斜向右下
解得
故A正确,BCD错误,
故选A。
5.C
细线被剪断的瞬间,因细线对甲的弹力突然消失,而引起上的张力发生突变,使甲的受力情况改变,瞬时加速度垂直斜向下方,大小为,方向垂直于斜向下方;当细线被剪断时,细线对乙的弹力突然消失,而弹簧的形变还来不及变化(变化要有一个过程,不能突变),因而弹簧的弹力不变,它与重力的合力与细线对乙的弹力是一对平衡力,等大反向,所以细线被剪断的瞬间,乙加速度的大小为,方向水平向右。甲乙两图中小球的加速度大小之比为
故选C。
6.B
剪断细绳的瞬间,细绳的张力立即消失,上面细绳的张力可突变,则A所受的上面细绳的拉力与重力重新平衡,A的加速度为0。
剪断绳子前,弹簧的弹力为
剪断绳子的瞬间,弹簧的弹力不变,隔离对C分析,合力为零,加速度为
对B分析,根据牛顿第二定律有,加速度为
故选B。
7.B
木板撤去前,小球处于平衡态,受重力、支持力和弹簧的拉力,如图
根据共点力平衡条件,有
代入数据解得
,
木板AB突然撤去后,支持力消失,重力和拉力不变,合力大小等于支持力N,方向与N反向,故加速度为
方向垂直于木板向下,故B正确错误,ACD。
故选B。
8.A
根据平衡状态受力分析可知,绳子拉力
烧断瞬间,弹簧弹力不变,弹簧和重力合力与绳子拉力大小相等,方向相反,所以
方向水平向右,故BCD错误,A正确。
故选A。
9.C
AB.小球静止时,分析受力情况,如图所示
由平衡条件得弹簧的弹力大小为
细绳的拉力大小为
故AB错误;
CD.细绳烧断瞬间弹簧的弹力不变,则小球所受的合力与烧断前细绳拉力的大小相等、方向相反,则此瞬间小球的加速度大小为
故C正确,D错误。
故选C。
10.D
AB.对A、B整体分析,沿斜面方向根据平衡条件可得
Fcosα=2mgsinα
解得
α=45°
对小球B进行受力分析,沿斜面方向由平衡条件可得
kx=mgsinα
解得
所以弹簧的原长为
故AB错误;
C.撤掉恒力F的瞬间,对A进行受力分析,沿斜面方向根据牛顿第二定律可得
mgsinα+kx=maA
小球A此时的加速度,故C错误;
D.撤掉恒力F的瞬间,弹簧弹力不变,B球所受合力不变,故B球的加速度为零,故D正确。
故选D。
11.D
对ab整体分析可知,整体受重力和绳子上的拉力,水平方向如果受墙的弹力,则整体不可能竖直静止,故不会受到水平方向上的弹力,根据平衡条件可知,细线上的拉力F=2mg;再对b分析可知,b只受重力和弹簧拉力而保持静止,故AB错误;由于b处于平衡,故弹簧的拉力F=mg,剪断细线瞬间弹簧的弹力不变,则对b分析可知,b受力不变,合力为零,故加速度为零,故C错误;对a分析可知,剪断细线瞬间a受重力和弹簧向下的拉力,合力Fa=2mg,则由牛顿第二定律可知,加速度为2g,故D正确.故选D.
12.CD
A.设a、b物体的质量为m,剪断细线前,对a、b整体受力分析,受到总重力和弹簧的弹力而平衡,故
再对物体a受力分析,受到重力、细线拉力和弹簧的拉力,剪断细线后,重力和弹簧的弹力不变,细线的拉力减为零,故物体a受到的力的合力等于mg,向上,根据牛顿第二定律得a的加速度为
方向向上,故A错误;
BCD.对物体b受力分析,受到重力、细线拉力,剪断细线后,重力不变,细线的拉力减为零,故物体b受到的力的合力等于mg,向下,根据牛顿第二定律得b的加速度为
方向向下,所以物体a的加速度与物体b的加速度大小相同,故B错误CD正确。
故选CD。
13.BD
AB.剪短弹簧瞬间,以A、B以及杆整体作为研究对象,整体做自由落体运动,加速度为;再隔离B,根据牛顿第二定律可知,小球B做自由落体运动,杆对B的力必须为零,故A错误,B正确;
CD.剪断轻杆瞬间, B球加速度大小为g,做自由落体运动;为剪短轻杆前对A进行受力分析如下
根据平衡条件有
当剪短轻杆后,对球A,除了杆的力消失意外,其他力没有发生变化,根据牛顿第二定律有
得
加速度方向竖直向上,故C错误,D正确。
故选BD。
14.AB
A.剪断轻绳瞬间,弹簧的形变还来不及恢复,即弹簧弹力不会突变,故A正确;
BC.剪断轻绳前,水平面对小球的弹力恰好为零,小球受重力、弹簧的弹力和细线的拉力作用处于平衡,对小球作受力分析,根据平衡条件和几何关系可知,弹簧弹力与小球重力大小相等,即
F=G=mg=10N
剪断轻绳的瞬间,地面对小球的滑动摩擦力为
Ff=μFN=μmg=2N
小球加速度
故B正确,C错误;
D.若剪断弹簧,轻绳对小球的拉力瞬间为零,此时小球所受的合力为零,则小球的加速度为零,故D错误。
故选AB。
