18 勾股定理(复习)
图片预览




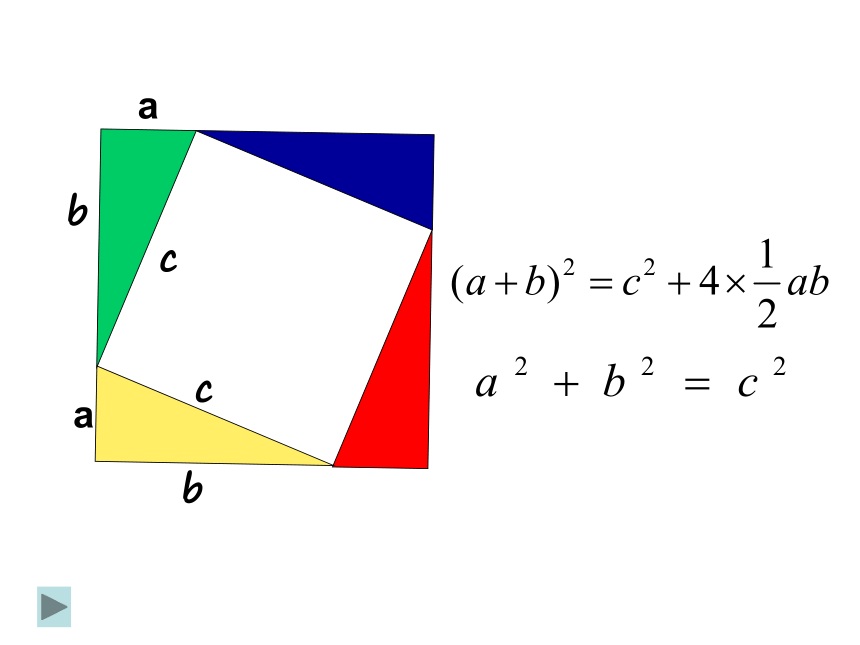



文档简介
(共32张PPT)
勾股定理(复习课)
问 题
1. 你能叙述勾股定理和逆定理的内容吗?
2. 你知道关于勾股定理的一些故事吗?
3. 你会证明勾股定理和逆定理吗?
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
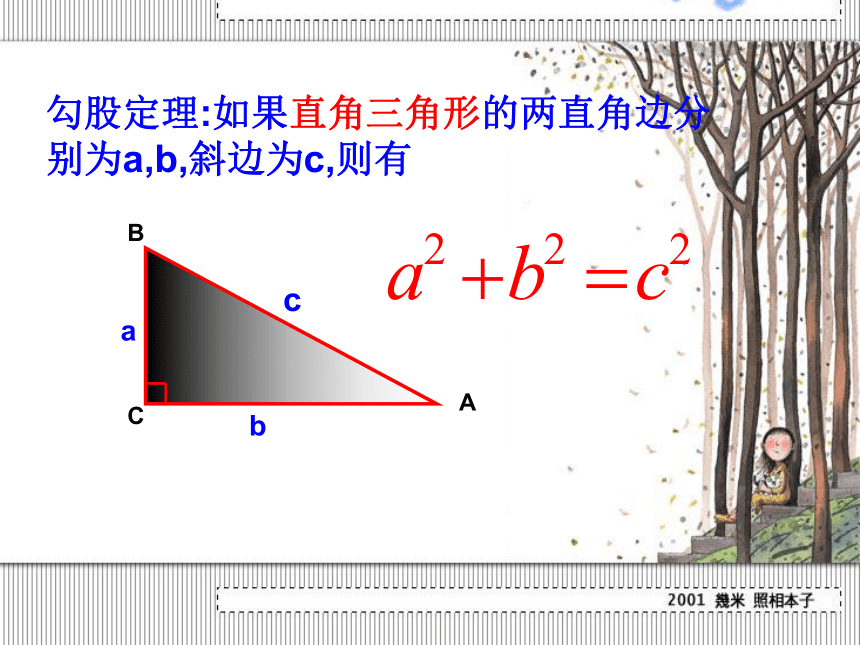
勾股定理:如果直角三角形的两直角边分 别为a,b,斜边为c,则有
A
B
C
a
b
c
a
c
b
a
b
c
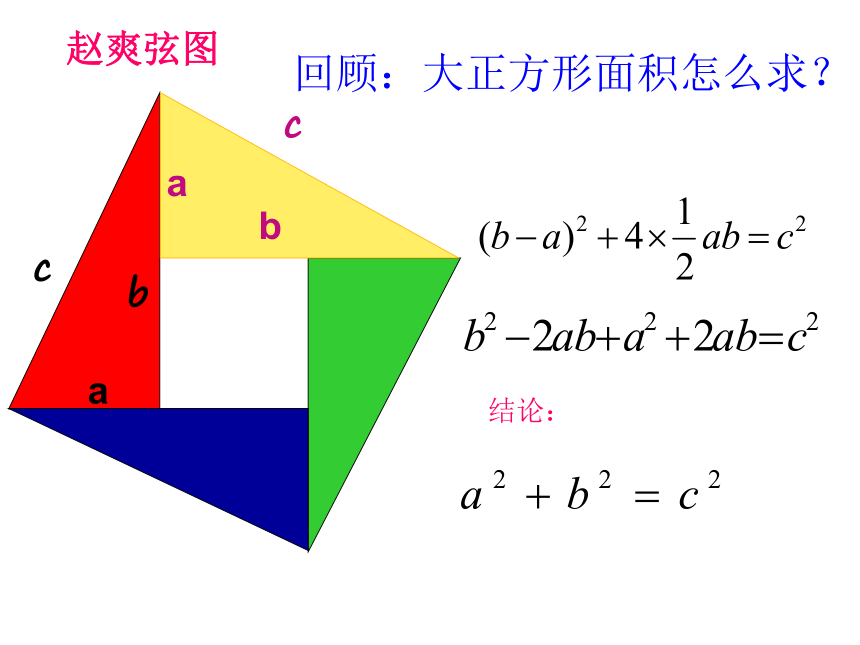
回顾:大正方形面积怎么求?
赵爽弦图
结论:
a
b
c
a
b
c
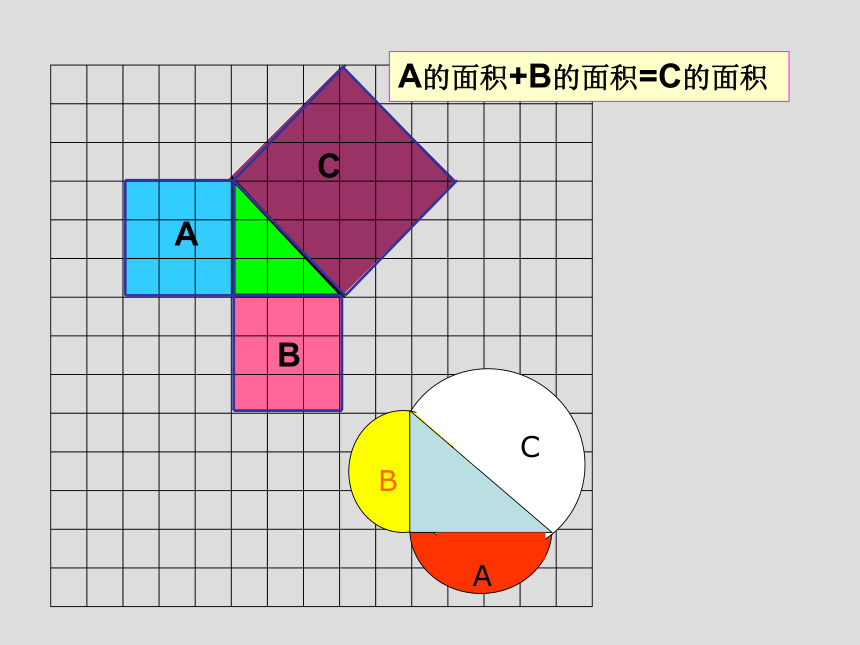
A
B
C
A的面积+B的面积=C的面积
D
A
B
C
一、分类思想
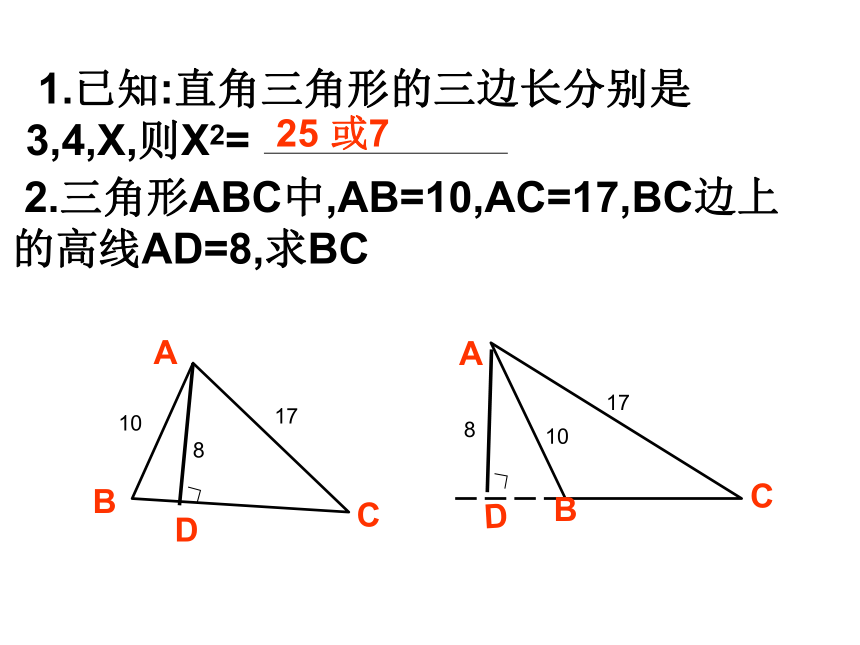
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
∟
D
∟
D
A
B
C
1.已知:直角三角形的三边长分别是3,4,X,则X2=
25
或7
A
B
C
10
17
8
17
10
8
分类思想
1.直角三角形中,已知两边长,直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
二、方程思想
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
2、我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题。
5
X+1
X
C
B
A
3、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求 1.CF 2.EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
4、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
三、展开思想
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?
1.5米
1.5米
2.2米
1.5米
1.5米
x
x
2.2米
A
B
C
X2=1.52+1.52=4.5
AB2=2.22+X2=9.34
AB≈3米
如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
10
20
B
A
C
15
5
10
20
B
5
B
5
10
20
A
C
E
F
E
10
20
A
C
F
A
E
C
B
20
15
10
5
如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
1. 几何体的表面路径最短的问题,一般展开表面成平面。
2.利用两点之间线段最短,及勾股定理求解。
展开思想
(1)在数轴上作出表示 的点
(2)如图是一个长为5宽为1的长方形,请你将它分割后重新拼成一个正方形,在长方形上画出分割线,并画出拼成的正方形。
(3)思考题:如图是一个长为4m宽为3m的长方形木料,截下一个长2m宽1m的小长方形后剩余的部分,请你将它适当分割后,重新拼成一个正方形,在上面画出分割线,并画出拼成的正方形。
请各小组讨论一下,举一个生活中的实例,并运用勾股定理来解决它。
再 见
勾股定理(复习课)
问 题
1. 你能叙述勾股定理和逆定理的内容吗?
2. 你知道关于勾股定理的一些故事吗?
3. 你会证明勾股定理和逆定理吗?
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾股定理:如果直角三角形的两直角边分 别为a,b,斜边为c,则有
A
B
C
a
b
c
a
c
b
a
b
c
回顾:大正方形面积怎么求?
赵爽弦图
结论:
a
b
c
a
b
c
A
B
C
A的面积+B的面积=C的面积
D
A
B
C
一、分类思想
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
∟
D
∟
D
A
B
C
1.已知:直角三角形的三边长分别是3,4,X,则X2=
25
或7
A
B
C
10
17
8
17
10
8
分类思想
1.直角三角形中,已知两边长,直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
二、方程思想
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
2、我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题。
5
X+1
X
C
B
A
3、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求 1.CF 2.EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
4、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
三、展开思想
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?
1.5米
1.5米
2.2米
1.5米
1.5米
x
x
2.2米
A
B
C
X2=1.52+1.52=4.5
AB2=2.22+X2=9.34
AB≈3米
如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
10
20
B
A
C
15
5
10
20
B
5
B
5
10
20
A
C
E
F
E
10
20
A
C
F
A
E
C
B
20
15
10
5
如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
1. 几何体的表面路径最短的问题,一般展开表面成平面。
2.利用两点之间线段最短,及勾股定理求解。
展开思想
(1)在数轴上作出表示 的点
(2)如图是一个长为5宽为1的长方形,请你将它分割后重新拼成一个正方形,在长方形上画出分割线,并画出拼成的正方形。
(3)思考题:如图是一个长为4m宽为3m的长方形木料,截下一个长2m宽1m的小长方形后剩余的部分,请你将它适当分割后,重新拼成一个正方形,在上面画出分割线,并画出拼成的正方形。
请各小组讨论一下,举一个生活中的实例,并运用勾股定理来解决它。
再 见
