多边形的内角和 课件
图片预览






文档简介
(共22张PPT)
多边形的内角和
生活中的多边形形象
多边形的内角和
教学目标
能说出多边形的概念,能正确识别多边形的边、顶点、内角、外角、对角线。
会推导多边形的内角和与外角和定理、并会应用它们进行有关多边形的边数、内角与外角的度数的计算。
此外,继续渗透类比与转化的思想,以培养学生由具体到抽象进行归纳、概括的能力。
由不在同一条直线上的 条线段首尾顺次相接组成的图形叫三角形。
在平面内,由不在同一条直线上的 条线段首尾顺次相接组成的图形叫四边形。
三
四
在平面内,由不在同一条直线上的 条线段首尾顺次相接组成的图形叫 边形。
n
n
1、多边形的边、顶点、内角、外角、对角
线的意义和四边形基本相同。
在平面内,由 线段首尾顺次相接组成的图形叫 边形。
一些
多
2、和四边形一样,多边形也有凹凸之分,
现在我们只研究凸多边形。
多边形的定义
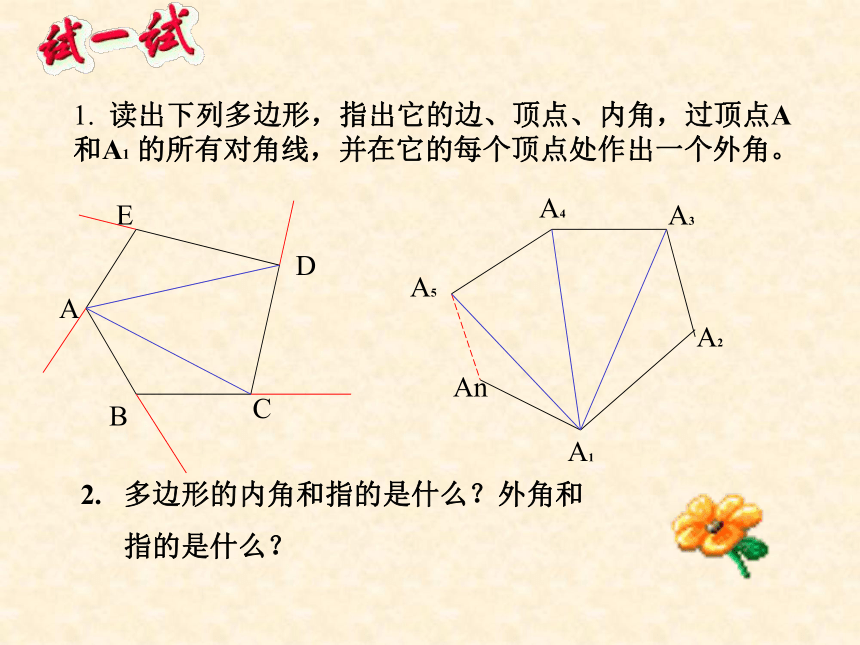
1. 读出下列多边形,指出它的边、顶点、内角,过顶点A 和A1 的所有对角线,并在它的每个顶点处作出一个外角。
D
A
E
B
C
多边形的内角和指的是什么?外角和
指的是什么?
A5
An
A1
A2
A3
A4
观察下列图形,从多边形的一个顶点出发可以引多少条对角线?这些对角线把多边形分成几个三角形?你能猜想 n 边形的内角和是多少度吗?
(1)
(6)
(5)
(4)
(3)
(2)
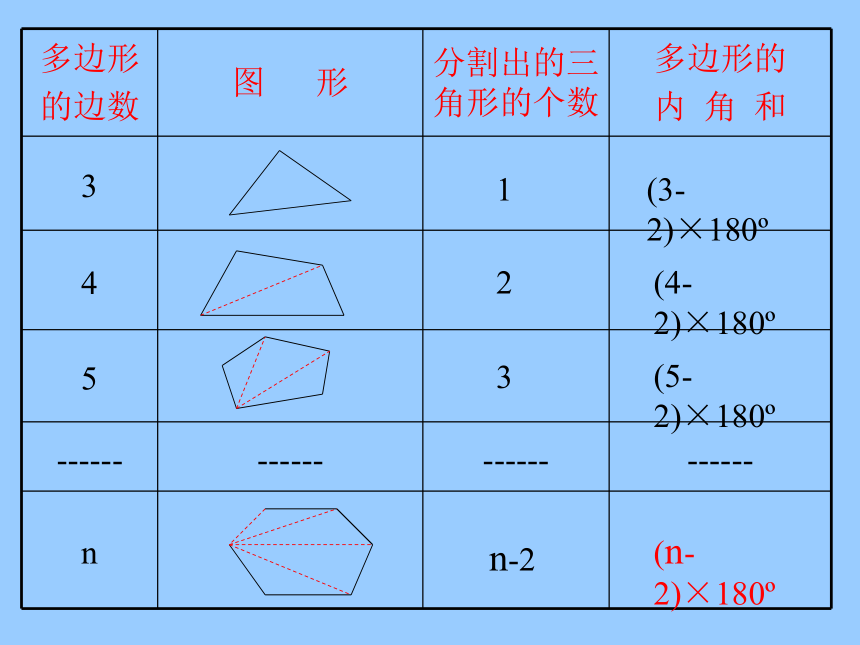
多边形
的边数 图 形 分割出的三角形的个数 多边形的
内 角 和
3
4
5
------ ------ ------ ------
n
n-2
1
2
3
(3-2)×180
(4-2)×180
(5-2)×180
(n-2)×180
多边形的内角和定理:
n边形的内角和等于(n-2)·180
∵过n 边形的一个顶点的所有对角线把n 边形分成 (n-2)个三角形,这(n-2)个三角形的内角和恰好是多边形的内角和,
∵三角形的内角和为180 ,
∴ n 边形的内角和等于(n-2)·180 。
你能用别的方法证明
这个定理吗?
证明:
证明多边形内角和定理的基本思想是什么?
推论:任意多边形的外角 和
等于360 。
类比前边的做法,你能归纳出n 边形的外角和是多少吗?
∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________
A1
A2
A3
An
A4
证明:
180 ,
(n-2) 180 ,
∴ n 边形的外角和等于n 180 – (n-2) 180 =360 。
n 180 ,
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:设多边形的边数为n ,
∵它的内角和等于(n-2) 180 ,外角
和等于360 ,
∴ (n-2)×180 =2 × 360
解得 n=6
∴这个多边形的边数6
一个多边形当边数增加1时,它的内角和增加多少度?
解:设边数为n ,则内角和等于(n-2) 180 ,
当边数增加1时,内角和等于(n+1-2) 180
∵ (n+1-2) 180 - (n-2) 180
=n 180 - 180 - n 180 +360
=180
∴内角和增加180
一、填空题
十二边形的内角和是( )。
正六边形的一个内角等于( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和等于它的外角和,这个多边形是( )边形。
一个多边形的内角和是720 ,则此多边形共有( )个内角。
1800
120
180
四
六
二、选择题
1、从 n边形的一个顶点出发作对角线,把这个多边形分
成三角形的个数是( )。
A、n B、n-1 C、n-2 D、n-3
2、n边形所有外角的个数是( )。
A、n B、2n C、3n D、不能确定
3、下列说法中,正确的是( )。
A、一个多边形的外角的个数与边数相同;
B、一个多边形的外角的个数是边数的2倍;
C、多边形的外角和是所有外角的和;
D、多边形的外角和是内角和的一半。
4、一个多边形每个外角都是30 ,这个多边形是( )。
A、十边形 B、十一边形 C、十二边形 D、十三边形
C
B
B
C
六角螺母的一个面是六边形的,这个六边形的六个内角相等,求每一个内角的度数。
一个多边形的内角和等于1080 ,求它的边数。
三、解答题
多边形的内角和公式
(n-2) 180 = n边形的内角和
什么时候可以顺向应用?什么时候可以逆向应用?
已知边数求多边形的内角和 — 直接应用内角和公式。
已知多边形的内角和求边数 — 逆向应用多边形内角和公式解关于n的方程。
1、三角形、四边形都属于多边形,所以四
边形的定义、边、顶点、内角、外角、
内角和、外角和、周长等概念可类比地
扩展到多边形。
2、n边形的内角和是(n-2)·180 ,揭示了多
边形的内角和与边数的关系:当边数增
加1时,内角和增加180 。
3、任意多边形的外角和都是360 ,与边数
无关。
多边形的内角和
小 结
在本课的学习中,同学们又一次体会到了类比、扩展、归纳、概括、从具体到抽象、化繁为简、化未知为已知等数学思想方法在数学中的应用。在平时的学习中,同学们应注意知识与知识之间的联系,灵活运用数学思想与方法,这样你才能体会到学习数学的乐趣,让数学成为你走向成功的助手。
复习课本59-62页
选做题:用两种方法证明多边形
内角和定理
完成63页习题4.1第5、6题
多边形的内角和
生活中的多边形形象
多边形的内角和
教学目标
能说出多边形的概念,能正确识别多边形的边、顶点、内角、外角、对角线。
会推导多边形的内角和与外角和定理、并会应用它们进行有关多边形的边数、内角与外角的度数的计算。
此外,继续渗透类比与转化的思想,以培养学生由具体到抽象进行归纳、概括的能力。
由不在同一条直线上的 条线段首尾顺次相接组成的图形叫三角形。
在平面内,由不在同一条直线上的 条线段首尾顺次相接组成的图形叫四边形。
三
四
在平面内,由不在同一条直线上的 条线段首尾顺次相接组成的图形叫 边形。
n
n
1、多边形的边、顶点、内角、外角、对角
线的意义和四边形基本相同。
在平面内,由 线段首尾顺次相接组成的图形叫 边形。
一些
多
2、和四边形一样,多边形也有凹凸之分,
现在我们只研究凸多边形。
多边形的定义
1. 读出下列多边形,指出它的边、顶点、内角,过顶点A 和A1 的所有对角线,并在它的每个顶点处作出一个外角。
D
A
E
B
C
多边形的内角和指的是什么?外角和
指的是什么?
A5
An
A1
A2
A3
A4
观察下列图形,从多边形的一个顶点出发可以引多少条对角线?这些对角线把多边形分成几个三角形?你能猜想 n 边形的内角和是多少度吗?
(1)
(6)
(5)
(4)
(3)
(2)
多边形
的边数 图 形 分割出的三角形的个数 多边形的
内 角 和
3
4
5
------ ------ ------ ------
n
n-2
1
2
3
(3-2)×180
(4-2)×180
(5-2)×180
(n-2)×180
多边形的内角和定理:
n边形的内角和等于(n-2)·180
∵过n 边形的一个顶点的所有对角线把n 边形分成 (n-2)个三角形,这(n-2)个三角形的内角和恰好是多边形的内角和,
∵三角形的内角和为180 ,
∴ n 边形的内角和等于(n-2)·180 。
你能用别的方法证明
这个定理吗?
证明:
证明多边形内角和定理的基本思想是什么?
推论:任意多边形的外角 和
等于360 。
类比前边的做法,你能归纳出n 边形的外角和是多少吗?
∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________
A1
A2
A3
An
A4
证明:
180 ,
(n-2) 180 ,
∴ n 边形的外角和等于n 180 – (n-2) 180 =360 。
n 180 ,
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:设多边形的边数为n ,
∵它的内角和等于(n-2) 180 ,外角
和等于360 ,
∴ (n-2)×180 =2 × 360
解得 n=6
∴这个多边形的边数6
一个多边形当边数增加1时,它的内角和增加多少度?
解:设边数为n ,则内角和等于(n-2) 180 ,
当边数增加1时,内角和等于(n+1-2) 180
∵ (n+1-2) 180 - (n-2) 180
=n 180 - 180 - n 180 +360
=180
∴内角和增加180
一、填空题
十二边形的内角和是( )。
正六边形的一个内角等于( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和等于它的外角和,这个多边形是( )边形。
一个多边形的内角和是720 ,则此多边形共有( )个内角。
1800
120
180
四
六
二、选择题
1、从 n边形的一个顶点出发作对角线,把这个多边形分
成三角形的个数是( )。
A、n B、n-1 C、n-2 D、n-3
2、n边形所有外角的个数是( )。
A、n B、2n C、3n D、不能确定
3、下列说法中,正确的是( )。
A、一个多边形的外角的个数与边数相同;
B、一个多边形的外角的个数是边数的2倍;
C、多边形的外角和是所有外角的和;
D、多边形的外角和是内角和的一半。
4、一个多边形每个外角都是30 ,这个多边形是( )。
A、十边形 B、十一边形 C、十二边形 D、十三边形
C
B
B
C
六角螺母的一个面是六边形的,这个六边形的六个内角相等,求每一个内角的度数。
一个多边形的内角和等于1080 ,求它的边数。
三、解答题
多边形的内角和公式
(n-2) 180 = n边形的内角和
什么时候可以顺向应用?什么时候可以逆向应用?
已知边数求多边形的内角和 — 直接应用内角和公式。
已知多边形的内角和求边数 — 逆向应用多边形内角和公式解关于n的方程。
1、三角形、四边形都属于多边形,所以四
边形的定义、边、顶点、内角、外角、
内角和、外角和、周长等概念可类比地
扩展到多边形。
2、n边形的内角和是(n-2)·180 ,揭示了多
边形的内角和与边数的关系:当边数增
加1时,内角和增加180 。
3、任意多边形的外角和都是360 ,与边数
无关。
多边形的内角和
小 结
在本课的学习中,同学们又一次体会到了类比、扩展、归纳、概括、从具体到抽象、化繁为简、化未知为已知等数学思想方法在数学中的应用。在平时的学习中,同学们应注意知识与知识之间的联系,灵活运用数学思想与方法,这样你才能体会到学习数学的乐趣,让数学成为你走向成功的助手。
复习课本59-62页
选做题:用两种方法证明多边形
内角和定理
完成63页习题4.1第5、6题
