五年级下册数学教案-4.5 组合体的体积 沪教版
文档属性
| 名称 | 五年级下册数学教案-4.5 组合体的体积 沪教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 444.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-14 00:00:00 | ||
图片预览


文档简介
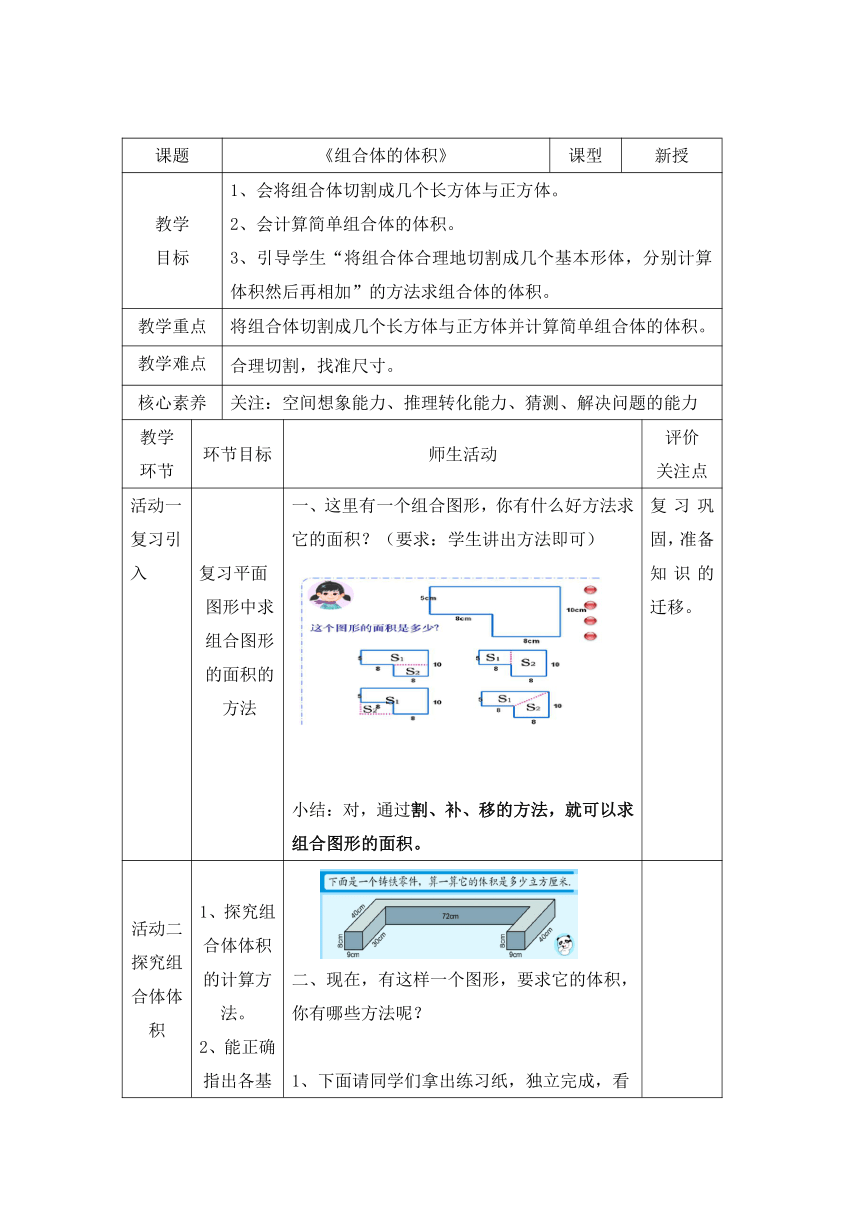
课题 《组合体的体积》 课型 新授
教学 目标 1、会将组合体切割成几个长方体与正方体。
2、会计算简单组合体的体积。
3、引导学生“将组合体合理地切割成几个基本形体,分别计算体积然后再相加”的方法求组合体的体积。
教学重点 将组合体切割成几个长方体与正方体并计算简单组合体的体积。
教学难点 合理切割,找准尺寸。
核心素养 关注:空间想象能力、推理转化能力、猜测、解决问题的能力
教学 环节 环节目标 师生活动 评价
关注点
活动一 复习引入
复习平面图形中求组合图形的面积的方法
一、这里有一个组合图形,你有什么好方法求它的面积?(要求:学生讲出方法即可)
小结:对,通过割、补、移的方法,就可以求组合图形的面积。 复习巩固,准备知识的迁移。
活动二 探究组合体体积
1、探究组合体体积的计算方法。
2、能正确指出各基本图形的长、宽、高。
二、现在,有这样一个图形,要求它的体积,你有哪些方法呢?
1、下面请同学们拿出练习纸,独立完成,看谁的方法又多又好?
2、将你的方法在小组内进行交流
3、全班交流
学生交流反馈:
法1
法2:
法3:
法4:
4、刚才,同学们想出了那么多方法来求组合体的体积,那么在解决这个问题的过程中,你有什么想说的,或者有什么要提醒大家的吗?
5、小结:(出示)
求组合体的体积:
A先将组合体分割或添补成几个基本形体,分别计算体积后,再相加减。
B、合理切割,找准每个长方体的长宽高数据。
6、介绍底面积×高的方法:
在巡视的过程中,老师发现有小朋友用了这样的方法,你能看懂吗?
板书:V= a b h
V= S h
思考:是所有的组合体都可以用底面积×高来求体积吗?(只有当高度一样时,我们可以用底面积×高求体积)
7、总结:看来,我们用割补等方法也能求出组合体的体积,在计算时注意合理切割,找准尺寸。
空间想象能力、转化的思想,合理解决
问题的意识、策略。
归纳、概括
活动三 实际运用 运用所学方法灵活、合理地计算组合体的体积。 三、巩固练习:
1、求下面各组合体的体积:(单位:厘米)
选择题:
1)下列式子中符合下图体积计算方法的是:C)
A、8×6×5+(24-8)×6×(15-5×2) +24×6×5
B、8×6×15+(24-8×2)×6 ×(15-5)+8×6×5
C、8×6×5+24×6×(15-5)+8×6×5
2)除了这种方法,还能怎么算?
横着分割:
8×6×5+(24-8)×6×(15-5×2) +24×6×5
竖着分割:
8×6×15+(24-8×2)×6 ×(15-5)+8×6×5
3)还可以怎么算?(割—移—底面积×高)
(媒体演示)
小结:我们可以根据组合体的特征进行割补移,然后找准每一个长方体的长宽高数据进行计算。
四、总结
今天你学到了什么?
思维的全面性灵活性
方法的合理性或最优化。
教学 目标 1、会将组合体切割成几个长方体与正方体。
2、会计算简单组合体的体积。
3、引导学生“将组合体合理地切割成几个基本形体,分别计算体积然后再相加”的方法求组合体的体积。
教学重点 将组合体切割成几个长方体与正方体并计算简单组合体的体积。
教学难点 合理切割,找准尺寸。
核心素养 关注:空间想象能力、推理转化能力、猜测、解决问题的能力
教学 环节 环节目标 师生活动 评价
关注点
活动一 复习引入
复习平面图形中求组合图形的面积的方法
一、这里有一个组合图形,你有什么好方法求它的面积?(要求:学生讲出方法即可)
小结:对,通过割、补、移的方法,就可以求组合图形的面积。 复习巩固,准备知识的迁移。
活动二 探究组合体体积
1、探究组合体体积的计算方法。
2、能正确指出各基本图形的长、宽、高。
二、现在,有这样一个图形,要求它的体积,你有哪些方法呢?
1、下面请同学们拿出练习纸,独立完成,看谁的方法又多又好?
2、将你的方法在小组内进行交流
3、全班交流
学生交流反馈:
法1
法2:
法3:
法4:
4、刚才,同学们想出了那么多方法来求组合体的体积,那么在解决这个问题的过程中,你有什么想说的,或者有什么要提醒大家的吗?
5、小结:(出示)
求组合体的体积:
A先将组合体分割或添补成几个基本形体,分别计算体积后,再相加减。
B、合理切割,找准每个长方体的长宽高数据。
6、介绍底面积×高的方法:
在巡视的过程中,老师发现有小朋友用了这样的方法,你能看懂吗?
板书:V= a b h
V= S h
思考:是所有的组合体都可以用底面积×高来求体积吗?(只有当高度一样时,我们可以用底面积×高求体积)
7、总结:看来,我们用割补等方法也能求出组合体的体积,在计算时注意合理切割,找准尺寸。
空间想象能力、转化的思想,合理解决
问题的意识、策略。
归纳、概括
活动三 实际运用 运用所学方法灵活、合理地计算组合体的体积。 三、巩固练习:
1、求下面各组合体的体积:(单位:厘米)
选择题:
1)下列式子中符合下图体积计算方法的是:C)
A、8×6×5+(24-8)×6×(15-5×2) +24×6×5
B、8×6×15+(24-8×2)×6 ×(15-5)+8×6×5
C、8×6×5+24×6×(15-5)+8×6×5
2)除了这种方法,还能怎么算?
横着分割:
8×6×5+(24-8)×6×(15-5×2) +24×6×5
竖着分割:
8×6×15+(24-8×2)×6 ×(15-5)+8×6×5
3)还可以怎么算?(割—移—底面积×高)
(媒体演示)
小结:我们可以根据组合体的特征进行割补移,然后找准每一个长方体的长宽高数据进行计算。
四、总结
今天你学到了什么?
思维的全面性灵活性
方法的合理性或最优化。
