2.5 匀变速直线运动与汽车安全驾驶同步练习—【新教材】粤教版(2019)高中物理必修第一册 (机构使用)(word含答案)
文档属性
| 名称 | 2.5 匀变速直线运动与汽车安全驾驶同步练习—【新教材】粤教版(2019)高中物理必修第一册 (机构使用)(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 65.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-14 06:22:16 | ||
图片预览



文档简介
粤教版(2019)高中物理必修第一册第二章匀变速直线运动第五节匀变速直线运动与汽车安全驾驶同步练习
选择题
1.做匀加速直线运动的物体,依次通过 A 、 B 、 C 三点,位移 sAB=sBC ,已知物体在 AB 段的平均速度大小为 2m/s ,在 BC 段的平均速度大小 3m/s ,那么物体在 B 点的瞬时速度大小为(?? )
A.?6.5m/s?????????????????????????????B.?2.4m/s?????????????????????????????C.?2.5m/s?????????????????????????????D.?2.6m/s
2.一辆沿笔直公路匀加速行驶的汽车,经过路旁两根相距60m的电线杆共用4s时间,它经过第二根电线杆时的速度是20m/s,则经过第一根电线杆时的速度为(?? )
A.?10 m/s????????????????????????????????B.?15m/s????????????????????????????????C.?5m/s????????????????????????????????D.?16 m/s
3.滑块以某一初速度冲上斜面做匀减速直线运动,到达斜面顶端时的速度恰好为零.已知滑块通过斜面中点时的速度为v,则滑块在整个斜面上的平均速度的大小为(? ?? )
A.?2+12v???????????????????????????????????B.?2v???????????????????????????????????C.?22v???????????????????????????????????D.?12v
4.如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则下列关于子弹依次射入每个木块时的速度比和穿过每个木块所用时间比的结论正确的是(?? )
A.?v1:v2:v3=3:2:1 B.?v1:v2:v3=5:3:1
C.?t1:t2:t3=1:2:3 D.?t1:t2:t3=(3?2):(2?1):1
5.平直公路上有一超声波测速仪B,汽车A离开B做直线运动。当两者相距325 m时刻,B发出超声波,同时A由于紧急情况刹车,当B接收到反射回来的超声波信号时,A恰好停止,此时刻AB相距345 m。已知超声波的声速为340 m/s,则汽车刹车的加速度大小为(?? )
A.?5 m/s2?????????????????????????????B.?7.5 m/s2?????????????????????????????C.?10 m/s2?????????????????????????????D.?无法确定
6.物体做匀加速直线运动,在时间T内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则物体(?? )
A.?在A点的速度大小为 x1+x22T B.?在B点的速度大小为 x1+3x22T
C.?运动的加速度为 2x1T2 D.?运动的加速度为 12
7.如图所示,小球从光滑斜面AC的顶端A处由静止开始做匀加速直线运动,B为AC的中点,下列说法中正确的是(???? )
A.?小球通过AB段与BC段所用时间之比为1:1
B.?小球在AB段与BC段的平均速度之比为 1:2
C.?小球在B点与C点的瞬时速度之比为 1:2
D.?小球在B点的瞬时速度与AC段的平均速度相等
8.P、Q、R三点在同一条直线上,一物体从P点静止开始做匀加速直线运动,经过Q 点的速度为v,到R点的速度为3v,则PQ∶QR等于 (?? )
A.?l∶8??????????????????????????????????????B.?l∶6??????????????????????????????????????C.?l∶5??????????????????????????????????????D.?1∶3
9.公路上行驶的汽车,司机从发现前方异常情况到紧急刹车,汽车仍将前进一段距离才能停下来。要保持安全,这段距离内不能有车辆和行人,因此把它称为安全距离。通常情况下,人的反应时间和汽车系统的反应时间之和为1s(这段时间汽车仍保持原速),刹车时汽车的加速度为 a=5m/s2 。若汽车以108km/h的速度行驶时,则其安全距离为(? )
A.?120m??????????????????????????????????B.?108m??????????????????????????????????C.?105m??????????????????????????????????D.?90m
10.如图所示,竖直圆环中有多条起始于A点的光滑轨道,其中AB通过环心O并保持竖直。一质点分别自A点沿各条轨道下滑,初速度均为零。那么,质点沿各轨道下滑的过程中,下列说法中正确的是(?? )
A.?质点沿着与AB夹角越大的轨道下滑,加速度越大
B.?质点沿着轨道AB下滑,时间最短
C.?轨道与AB夹角越小 (AB 除外 ) ,滑到底端时速率越大
D.?无论沿图中哪条轨道下滑,所用的时间均不同
11.已知某型战斗机在航行的航空母舰上起飞(无风),起飞时的加速度可达5m/s2 , 飞机起飞速度需达到40m/s,若飞机必须在滑行120m后起飞,问航空母舰行驶的速度至少为(??? )
A.?5m/s?????????????????????????????????B.?10m/s?????????????????????????????????C.?15m/s?????????????????????????????????D.?20m/s
12.航空母舰上都有帮助飞机起飞的弹射系统,已知“F—A15”型战斗机在跑道上加速时产生的加速度为 4.5m/s2 ,起飞速度为 50m/s 。若该飞机滑行100m时起飞,则弹射系统必须使飞机具有的初速度为( ??)
A.?20m/s????????????????????????????????B.?30m/s????????????????????????????????C.?40m/s????????????????????????????????D.?60m/s
13.如图所示,A、B两物体在同一直线上运动,当它们相距s=7m时,A在水平拉力和摩擦力的作用下,正以4m/s的速度向右做匀速运动,而物体B此时速度为10m/s,方向向右,它在摩擦力作用下做匀减速运动,加速度大小为2m/s2 , 则A追上B用的时间为:(? )
A.?6s?????????????????????????????????????????B.?7s?????????????????????????????????????????C.?8s?????????????????????????????????????????D.?9s
14.某物体做直线运动,物体的速度—时间图线如图所示,若初速度的大小为v1 , 末速度的大小为v2 , 则在时间t1内物体的平均速度是( ??)
A.?等于(v1+v2)/2?????????B.?小于(v1+v2)/2?????????C.?大于(v1+v2)/2?????????D.?条件不足,无法比较
15.物体从静止开始做匀加速直线运动,从零时刻开始,连续通过三段位移时间分别为1秒、2秒、3秒。下列说法正确的是(??? )
A.?三段位移之比为1:9:36;???????????????????????????????B.?三段位移的末速度之比为1:2:3;
C.?三段位移的平均速度之比为1:3:5;???????????????D.?三段位移的平均速度之比为1:4:9
16.一个从地面上竖直上抛的物体,不计空气阻力。它两次经过一个较低点A的时间间隔是7 s,两次经过一个较高点B的时间间隔是3 s,重力加速度g取10 m/s2 , 则AB之间的距离是( ??)
A.?50m??????????????????????????B.?80m??????????????????????????C.?200m??????????????????????????D.?初速度未知,无法确定
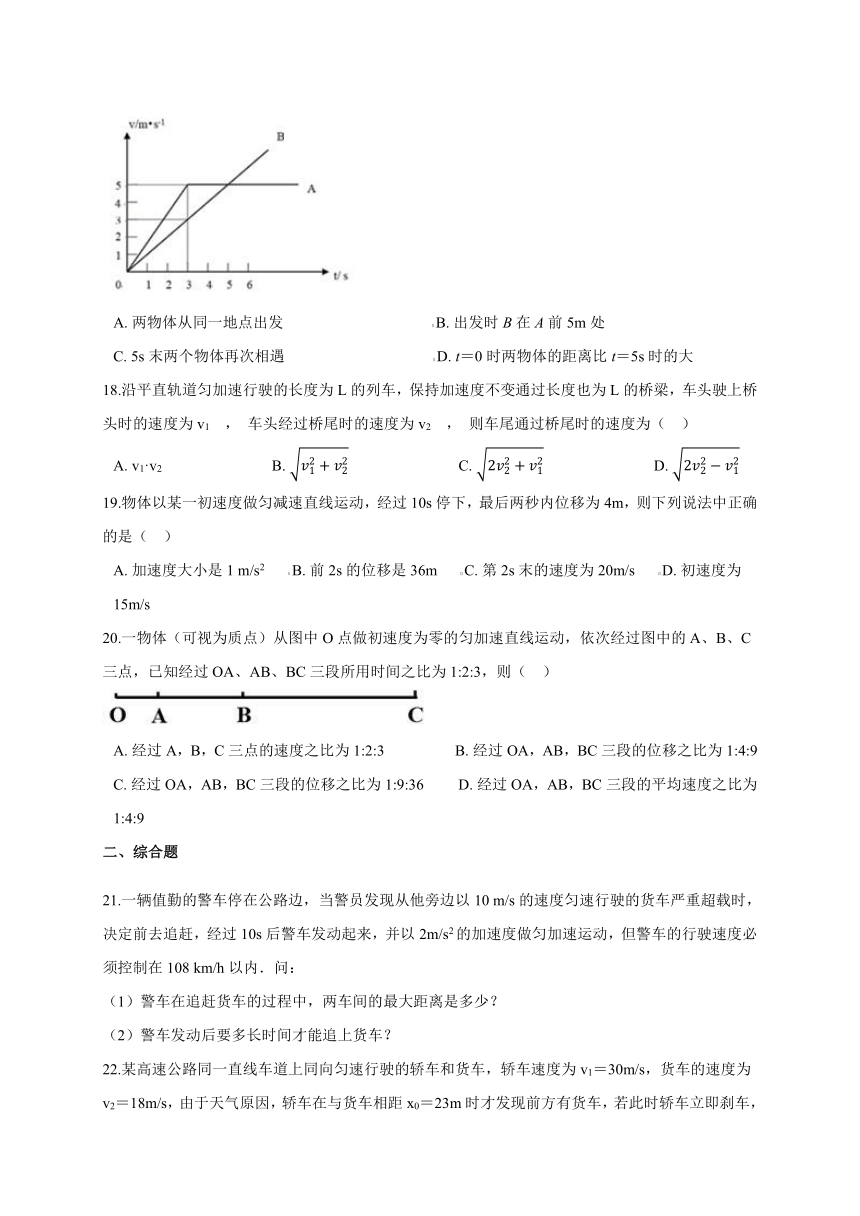
17.A和B两质点在同一直线上运动的v-t图象如图所示,已知在第3s末两个物体在途中相遇,则下列说法正确的是(? ?)
A.?两物体从同一地点出发???????????????????????????????????????B.?出发时B在A前5m处
C.?5s末两个物体再次相遇???????????????????????????????????????D.?t=0时两物体的距离比t=5s时的大
18.沿平直轨道匀加速行驶的长度为L的列车,保持加速度不变通过长度也为L的桥梁,车头驶上桥头时的速度为v1 , 车头经过桥尾时的速度为v2 , 则车尾通过桥尾时的速度为(?? )
A.?v1·v2?????????????????????????????B.?v12+v22?????????????????????????????C.?2v22+v12?????????????????????????????D.?2v22?v12
19.物体以某一初速度做匀减速直线运动,经过10s停下,最后两秒内位移为4m,则下列说法中正确的是(?? )
A.?加速度大小是1 m/s2??????B.?前2s的位移是36m??????C.?第2s末的速度为20m/s??????D.?初速度为15m/s
20.一物体(可视为质点)从图中O点做初速度为零的匀加速直线运动,依次经过图中的A、B、C三点,已知经过OA、AB、BC三段所用时间之比为1:2:3,则( ??)
A.?经过A,B,C三点的速度之比为1:2:3??????????????????B.?经过OA,AB,BC三段的位移之比为1:4:9
C.?经过OA,AB,BC三段的位移之比为1:9:36????????D.?经过OA,AB,BC三段的平均速度之比为1:4:9
综合题
21.一辆值勤的警车停在公路边,当警员发现从他旁边以10 m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过10s后警车发动起来,并以2m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在108 km/h以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
22.某高速公路同一直线车道上同向匀速行驶的轿车和货车,轿车速度为v1=30m/s,货车的速度为v2=18m/s,由于天气原因,轿车在与货车相距x0=23m时才发现前方有货车,若此时轿车立即刹车,则轿车要经过150m才停下来。刹车过程可视为匀减速运动,运动过程中两车均可视为质点。
(1)若轿车刹车后货车继续以v2=18m/s的速度匀速行驶,请通过计算分析两车是否会相撞?
(2)若轿车在刹车的同时给货车发信号,货车司机经t0=1.5s收到信号并立即以加速度大小a2=2m/s2匀加速前进,请通过计算分析两车是否会相撞。若不相撞,求此过程中轿车与货车的最近距离为多少。
23.小明沿平直人行道以v1=1m/s的速度向公交车站走去搭乘公交车上学.在距车站x=50m时,发现一辆公交车正以v2=15m/s的速度从身旁的平直公路同向驶向公交车站.为了乘上该公交车,他立即匀加速向前跑去,加速过程的最大加速度a1=2.5m/s2、能达到的最大速度vm=6m/s.假设公交车行驶到距车站x0=25m处开始刹车并恰好到车站停下,停车t=10s后重新启动向前开去.不计公交车车长,公交车刹车过程可视为匀减速直线运动.
(1)求公交车刹车过程加速度的大小a2;
(2)求小明开始加速至抵达公交车站所需的最短时间t(计算结果保留2位有效数字);
(3)通过计算分析小明能否乘上该公交车。
24.羚羊从静止开始奔跑,经过 50m 的距离能加速到最大速度 25m/s,并能维持一段较长的时间。猎豹从静止开始奔跑,经过 60m 的距离能加速到最大速度 30m/s,以后只能维持4.0s,然后做加速度大小是 2.5m/s2 的匀减速直线运动。设猎豹距离羚羊x时开始攻击, 羚羊则在猎豹开始攻击后1.0s才开始奔跑。假设羚羊和猎豹在加速阶段分别做匀加速运动,且均沿同一直线奔跑,求:
(1)羚羊、猎豹的加速度大小和加速时间分别是多少;
(2)猎豹要在其加速阶段追上羚羊,x值应在什么范围;
(3)猎豹要在从最大速度减速前追到羚羊,x应取什么值;
(4)羚羊最终没有被猎豹追上,x 值应在什么范围。
参考答案
1. D 2. A 3. C 4. D 5. C 6. A 7. C 8. A 9. A 10. C 11. A 12. C 13. C 14. B 15. D 16. A 17. D 18. D 19. B 20. D
21.【答案】 (1)解:已知vm=108km/h=30m/s,v=10m/s,a=2m/s2
当两车速度相等时,两车间的距离最大,速度相等经历的时间为: t1=va=102s=5s
此时货车的位移为:x1=v(t1+10)=10×15m=150m
警车的位移为: x2=12at12=12×2×52=25m ?
则两车间的最大距离为:△x=x1-x2=150m-25m=125m
(2)解:警车加速到最大速度所需的时间为: t2=vma=302s=15s
此时警车的位移为: x′2=12at22=12×2×152m=225m
货车的位移为:x1′=v(t2+10)=10×25m=250m
两车还相距?x=25m,说明警车还没有追上货车.
设警车再经过t时间追上货车,则有: vmt?vt=Δx
代入数据解得:t=1.25s
则警车发动后追上货车的时间为15s+1.25s=16.25s
【解析】(1)警车做匀加速直线运动,货车做匀加速直线运动,两车速度相等时距离最大,利用共速可以求出共速的时间,结合两车的位移公式可以求出两车最大的距离;
(2)警车做匀加速直线运动,利用最大速度和速度公式可以求出加速的时间,利用位移公式可以判别警车还需要继续做匀速运动才可以追上货车,利用匀速运动的位移公式可以求出继续运动的时间。
22.【答案】 (1)解:对轿车刹车的过程做匀减速运动,有: v12=2a1x ,解得轿车刹车过程的加速度大小 a1=3m/s2
当两车的速度相等时是避免碰撞的临界条件,则有 v1?a1t1=v2
解得t1=4s
轿车行驶的距离x1= v1+v22 t1=96m
货车行驶的距离x2=v2t1=72m
因 x1?x2=24m>x0=23m
所以两车会相撞
(2)解:假设从轿车开始刹车经过时间t,两车速度相等,即: v1?a1t=v2+a2(t?t0)
解得t=3s
轿车行驶的距离 x1'=v1t?12a1t2 ,货车行驶的距离 x2'=v2t0+v2(t?t0)+12a2(t?t0)2
解得x1′=76.5m
x2′=56.25m
因 x1′?x2′=20.25m所以两车不会相撞, 在避撞过程中,由于轿车做减速运动而货车做加速运动,则两车的速度相等时是两者距离最近,最近距离为20.25m
【解析】(1)轿车做匀减速直线运动,利用速度位移公式可以求出轿车加速度的大小;利用两车速度大小相等,结合速度公式可以求出共速的时间;再利用两车的位移公式可以判别两车是否相遇;
(2)假设轿车开始减速,而货车开始做匀加速直线运动;利用共速结合速度公式可以求出共速的时间,结合两车的位移公式可以判别两车是否相遇。
23.【答案】 (1)解:公交车做匀减速运动过程,根据速度位移公式 v22=2a2x0
解得a2=4.5m/s2
(2)解:小明以最大加速度达到最大速度用时 t3=vm?v1a1=2s
加速过程的位移 x′=v1+vm2t3=7m
以最大速度跑到车站所用的时间 t4=x?x′vm=436≈7.2s
小明从开始加速至抵达公交车站所需的最短时间 t′=t3+t4≈9.2s
(3)解:公交车从相遇处到开始刹车用时 t1=x?x0v2=53s
公交车刹车过程中用时 t2=v2a2=103s
公交车从与小明相遇到再次重新启动用时由于 t′【解析】(1)公交车做匀减速直线运动,利用速度位移公式可以求出加速度的大小;
(2)学生先做匀加速直线运动,再做匀速直线运动,利用速度公式可以求出加速的时间,利用平均速度公式可以求出匀加速的位移,再利用匀速运动的位移公式可以求出匀速运动的时间;
(3)公车刚开始做匀速运动,利用匀速运动的位移公式可以求出运动的时间,结合速度公式可以求出刹车的时间,与学生运动时间比较可以判别小明可以乘上公车。
24.【答案】 (1)解;羚羊加速阶段需要时间 t1=x1v1=50m25m/s+02=4s
羚羊加速度 a1=v1t1=6.25m/s2
猎豹加速阶段需要时间 t2=x2v2=60m30m/s+02=4s
猎豹加速度 a2=v2t2=7.5m/s2
(2)解;猎豹在加速阶段运动距离为 x2=60m
而羚羊在这段时间内运动的距离为 x1=12a1(t1?1s)2=2258m
根据题意有 x2≥x1+x
即 x≤x2?x1=31.875m≈32m
(3)解;猎豹从开始攻击到开始减速运动的距离为 x′2=60m+30m/s×4s=180m 而羚羊在这段时间内的运动距离为 x′1=50m+25m/s×(4s?1s)=125m
根据题意有 x′2≥x′1+x′
即 x′≤x′2?x′1=180m?125m=55m
(4)解;当猎豹的速度减小到跟羚羊的速度相等时,如果还没追上羚羊,则最终不会追上了。这个过程猎豹减速的时间为 t=v2?v1a=2s
减速阶段,猎豹比羚羊多跑的距离为 Δx=(30+252×2?25×2)m=5m
根据题意有 x″≥x+Δx=60m
【解析】(1)羚羊和猎豹都做匀加速直线运动;利用平均速度公式可以求出加速的时间,结合速度公式可以求出加速度的大小;
(2)羚羊做匀加速直线运动,利用位移公式可以求出羚羊运动的位移,结合猎豹在加速段运动的位移大小可以求出两者的距离大小;
(3)猎豹先加速后运动运动,利用位移公式可以求出运动的距离;结合羚羊先加速后匀速运动的位移,可以求出两者之间的距离;
(4)当猎豹和羚羊的速度相等时,利用速度公式可以求出猎豹减速的时间,结合位移公式可以求出羚羊没被追上的距离大小。
选择题
1.做匀加速直线运动的物体,依次通过 A 、 B 、 C 三点,位移 sAB=sBC ,已知物体在 AB 段的平均速度大小为 2m/s ,在 BC 段的平均速度大小 3m/s ,那么物体在 B 点的瞬时速度大小为(?? )
A.?6.5m/s?????????????????????????????B.?2.4m/s?????????????????????????????C.?2.5m/s?????????????????????????????D.?2.6m/s
2.一辆沿笔直公路匀加速行驶的汽车,经过路旁两根相距60m的电线杆共用4s时间,它经过第二根电线杆时的速度是20m/s,则经过第一根电线杆时的速度为(?? )
A.?10 m/s????????????????????????????????B.?15m/s????????????????????????????????C.?5m/s????????????????????????????????D.?16 m/s
3.滑块以某一初速度冲上斜面做匀减速直线运动,到达斜面顶端时的速度恰好为零.已知滑块通过斜面中点时的速度为v,则滑块在整个斜面上的平均速度的大小为(? ?? )
A.?2+12v???????????????????????????????????B.?2v???????????????????????????????????C.?22v???????????????????????????????????D.?12v
4.如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则下列关于子弹依次射入每个木块时的速度比和穿过每个木块所用时间比的结论正确的是(?? )
A.?v1:v2:v3=3:2:1 B.?v1:v2:v3=5:3:1
C.?t1:t2:t3=1:2:3 D.?t1:t2:t3=(3?2):(2?1):1
5.平直公路上有一超声波测速仪B,汽车A离开B做直线运动。当两者相距325 m时刻,B发出超声波,同时A由于紧急情况刹车,当B接收到反射回来的超声波信号时,A恰好停止,此时刻AB相距345 m。已知超声波的声速为340 m/s,则汽车刹车的加速度大小为(?? )
A.?5 m/s2?????????????????????????????B.?7.5 m/s2?????????????????????????????C.?10 m/s2?????????????????????????????D.?无法确定
6.物体做匀加速直线运动,在时间T内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则物体(?? )
A.?在A点的速度大小为 x1+x22T B.?在B点的速度大小为 x1+3x22T
C.?运动的加速度为 2x1T2 D.?运动的加速度为 12
7.如图所示,小球从光滑斜面AC的顶端A处由静止开始做匀加速直线运动,B为AC的中点,下列说法中正确的是(???? )
A.?小球通过AB段与BC段所用时间之比为1:1
B.?小球在AB段与BC段的平均速度之比为 1:2
C.?小球在B点与C点的瞬时速度之比为 1:2
D.?小球在B点的瞬时速度与AC段的平均速度相等
8.P、Q、R三点在同一条直线上,一物体从P点静止开始做匀加速直线运动,经过Q 点的速度为v,到R点的速度为3v,则PQ∶QR等于 (?? )
A.?l∶8??????????????????????????????????????B.?l∶6??????????????????????????????????????C.?l∶5??????????????????????????????????????D.?1∶3
9.公路上行驶的汽车,司机从发现前方异常情况到紧急刹车,汽车仍将前进一段距离才能停下来。要保持安全,这段距离内不能有车辆和行人,因此把它称为安全距离。通常情况下,人的反应时间和汽车系统的反应时间之和为1s(这段时间汽车仍保持原速),刹车时汽车的加速度为 a=5m/s2 。若汽车以108km/h的速度行驶时,则其安全距离为(? )
A.?120m??????????????????????????????????B.?108m??????????????????????????????????C.?105m??????????????????????????????????D.?90m
10.如图所示,竖直圆环中有多条起始于A点的光滑轨道,其中AB通过环心O并保持竖直。一质点分别自A点沿各条轨道下滑,初速度均为零。那么,质点沿各轨道下滑的过程中,下列说法中正确的是(?? )
A.?质点沿着与AB夹角越大的轨道下滑,加速度越大
B.?质点沿着轨道AB下滑,时间最短
C.?轨道与AB夹角越小 (AB 除外 ) ,滑到底端时速率越大
D.?无论沿图中哪条轨道下滑,所用的时间均不同
11.已知某型战斗机在航行的航空母舰上起飞(无风),起飞时的加速度可达5m/s2 , 飞机起飞速度需达到40m/s,若飞机必须在滑行120m后起飞,问航空母舰行驶的速度至少为(??? )
A.?5m/s?????????????????????????????????B.?10m/s?????????????????????????????????C.?15m/s?????????????????????????????????D.?20m/s
12.航空母舰上都有帮助飞机起飞的弹射系统,已知“F—A15”型战斗机在跑道上加速时产生的加速度为 4.5m/s2 ,起飞速度为 50m/s 。若该飞机滑行100m时起飞,则弹射系统必须使飞机具有的初速度为( ??)
A.?20m/s????????????????????????????????B.?30m/s????????????????????????????????C.?40m/s????????????????????????????????D.?60m/s
13.如图所示,A、B两物体在同一直线上运动,当它们相距s=7m时,A在水平拉力和摩擦力的作用下,正以4m/s的速度向右做匀速运动,而物体B此时速度为10m/s,方向向右,它在摩擦力作用下做匀减速运动,加速度大小为2m/s2 , 则A追上B用的时间为:(? )
A.?6s?????????????????????????????????????????B.?7s?????????????????????????????????????????C.?8s?????????????????????????????????????????D.?9s
14.某物体做直线运动,物体的速度—时间图线如图所示,若初速度的大小为v1 , 末速度的大小为v2 , 则在时间t1内物体的平均速度是( ??)
A.?等于(v1+v2)/2?????????B.?小于(v1+v2)/2?????????C.?大于(v1+v2)/2?????????D.?条件不足,无法比较
15.物体从静止开始做匀加速直线运动,从零时刻开始,连续通过三段位移时间分别为1秒、2秒、3秒。下列说法正确的是(??? )
A.?三段位移之比为1:9:36;???????????????????????????????B.?三段位移的末速度之比为1:2:3;
C.?三段位移的平均速度之比为1:3:5;???????????????D.?三段位移的平均速度之比为1:4:9
16.一个从地面上竖直上抛的物体,不计空气阻力。它两次经过一个较低点A的时间间隔是7 s,两次经过一个较高点B的时间间隔是3 s,重力加速度g取10 m/s2 , 则AB之间的距离是( ??)
A.?50m??????????????????????????B.?80m??????????????????????????C.?200m??????????????????????????D.?初速度未知,无法确定
17.A和B两质点在同一直线上运动的v-t图象如图所示,已知在第3s末两个物体在途中相遇,则下列说法正确的是(? ?)
A.?两物体从同一地点出发???????????????????????????????????????B.?出发时B在A前5m处
C.?5s末两个物体再次相遇???????????????????????????????????????D.?t=0时两物体的距离比t=5s时的大
18.沿平直轨道匀加速行驶的长度为L的列车,保持加速度不变通过长度也为L的桥梁,车头驶上桥头时的速度为v1 , 车头经过桥尾时的速度为v2 , 则车尾通过桥尾时的速度为(?? )
A.?v1·v2?????????????????????????????B.?v12+v22?????????????????????????????C.?2v22+v12?????????????????????????????D.?2v22?v12
19.物体以某一初速度做匀减速直线运动,经过10s停下,最后两秒内位移为4m,则下列说法中正确的是(?? )
A.?加速度大小是1 m/s2??????B.?前2s的位移是36m??????C.?第2s末的速度为20m/s??????D.?初速度为15m/s
20.一物体(可视为质点)从图中O点做初速度为零的匀加速直线运动,依次经过图中的A、B、C三点,已知经过OA、AB、BC三段所用时间之比为1:2:3,则( ??)
A.?经过A,B,C三点的速度之比为1:2:3??????????????????B.?经过OA,AB,BC三段的位移之比为1:4:9
C.?经过OA,AB,BC三段的位移之比为1:9:36????????D.?经过OA,AB,BC三段的平均速度之比为1:4:9
综合题
21.一辆值勤的警车停在公路边,当警员发现从他旁边以10 m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过10s后警车发动起来,并以2m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在108 km/h以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
22.某高速公路同一直线车道上同向匀速行驶的轿车和货车,轿车速度为v1=30m/s,货车的速度为v2=18m/s,由于天气原因,轿车在与货车相距x0=23m时才发现前方有货车,若此时轿车立即刹车,则轿车要经过150m才停下来。刹车过程可视为匀减速运动,运动过程中两车均可视为质点。
(1)若轿车刹车后货车继续以v2=18m/s的速度匀速行驶,请通过计算分析两车是否会相撞?
(2)若轿车在刹车的同时给货车发信号,货车司机经t0=1.5s收到信号并立即以加速度大小a2=2m/s2匀加速前进,请通过计算分析两车是否会相撞。若不相撞,求此过程中轿车与货车的最近距离为多少。
23.小明沿平直人行道以v1=1m/s的速度向公交车站走去搭乘公交车上学.在距车站x=50m时,发现一辆公交车正以v2=15m/s的速度从身旁的平直公路同向驶向公交车站.为了乘上该公交车,他立即匀加速向前跑去,加速过程的最大加速度a1=2.5m/s2、能达到的最大速度vm=6m/s.假设公交车行驶到距车站x0=25m处开始刹车并恰好到车站停下,停车t=10s后重新启动向前开去.不计公交车车长,公交车刹车过程可视为匀减速直线运动.
(1)求公交车刹车过程加速度的大小a2;
(2)求小明开始加速至抵达公交车站所需的最短时间t(计算结果保留2位有效数字);
(3)通过计算分析小明能否乘上该公交车。
24.羚羊从静止开始奔跑,经过 50m 的距离能加速到最大速度 25m/s,并能维持一段较长的时间。猎豹从静止开始奔跑,经过 60m 的距离能加速到最大速度 30m/s,以后只能维持4.0s,然后做加速度大小是 2.5m/s2 的匀减速直线运动。设猎豹距离羚羊x时开始攻击, 羚羊则在猎豹开始攻击后1.0s才开始奔跑。假设羚羊和猎豹在加速阶段分别做匀加速运动,且均沿同一直线奔跑,求:
(1)羚羊、猎豹的加速度大小和加速时间分别是多少;
(2)猎豹要在其加速阶段追上羚羊,x值应在什么范围;
(3)猎豹要在从最大速度减速前追到羚羊,x应取什么值;
(4)羚羊最终没有被猎豹追上,x 值应在什么范围。
参考答案
1. D 2. A 3. C 4. D 5. C 6. A 7. C 8. A 9. A 10. C 11. A 12. C 13. C 14. B 15. D 16. A 17. D 18. D 19. B 20. D
21.【答案】 (1)解:已知vm=108km/h=30m/s,v=10m/s,a=2m/s2
当两车速度相等时,两车间的距离最大,速度相等经历的时间为: t1=va=102s=5s
此时货车的位移为:x1=v(t1+10)=10×15m=150m
警车的位移为: x2=12at12=12×2×52=25m ?
则两车间的最大距离为:△x=x1-x2=150m-25m=125m
(2)解:警车加速到最大速度所需的时间为: t2=vma=302s=15s
此时警车的位移为: x′2=12at22=12×2×152m=225m
货车的位移为:x1′=v(t2+10)=10×25m=250m
两车还相距?x=25m,说明警车还没有追上货车.
设警车再经过t时间追上货车,则有: vmt?vt=Δx
代入数据解得:t=1.25s
则警车发动后追上货车的时间为15s+1.25s=16.25s
【解析】(1)警车做匀加速直线运动,货车做匀加速直线运动,两车速度相等时距离最大,利用共速可以求出共速的时间,结合两车的位移公式可以求出两车最大的距离;
(2)警车做匀加速直线运动,利用最大速度和速度公式可以求出加速的时间,利用位移公式可以判别警车还需要继续做匀速运动才可以追上货车,利用匀速运动的位移公式可以求出继续运动的时间。
22.【答案】 (1)解:对轿车刹车的过程做匀减速运动,有: v12=2a1x ,解得轿车刹车过程的加速度大小 a1=3m/s2
当两车的速度相等时是避免碰撞的临界条件,则有 v1?a1t1=v2
解得t1=4s
轿车行驶的距离x1= v1+v22 t1=96m
货车行驶的距离x2=v2t1=72m
因 x1?x2=24m>x0=23m
所以两车会相撞
(2)解:假设从轿车开始刹车经过时间t,两车速度相等,即: v1?a1t=v2+a2(t?t0)
解得t=3s
轿车行驶的距离 x1'=v1t?12a1t2 ,货车行驶的距离 x2'=v2t0+v2(t?t0)+12a2(t?t0)2
解得x1′=76.5m
x2′=56.25m
因 x1′?x2′=20.25m
【解析】(1)轿车做匀减速直线运动,利用速度位移公式可以求出轿车加速度的大小;利用两车速度大小相等,结合速度公式可以求出共速的时间;再利用两车的位移公式可以判别两车是否相遇;
(2)假设轿车开始减速,而货车开始做匀加速直线运动;利用共速结合速度公式可以求出共速的时间,结合两车的位移公式可以判别两车是否相遇。
23.【答案】 (1)解:公交车做匀减速运动过程,根据速度位移公式 v22=2a2x0
解得a2=4.5m/s2
(2)解:小明以最大加速度达到最大速度用时 t3=vm?v1a1=2s
加速过程的位移 x′=v1+vm2t3=7m
以最大速度跑到车站所用的时间 t4=x?x′vm=436≈7.2s
小明从开始加速至抵达公交车站所需的最短时间 t′=t3+t4≈9.2s
(3)解:公交车从相遇处到开始刹车用时 t1=x?x0v2=53s
公交车刹车过程中用时 t2=v2a2=103s
公交车从与小明相遇到再次重新启动用时由于 t′
(2)学生先做匀加速直线运动,再做匀速直线运动,利用速度公式可以求出加速的时间,利用平均速度公式可以求出匀加速的位移,再利用匀速运动的位移公式可以求出匀速运动的时间;
(3)公车刚开始做匀速运动,利用匀速运动的位移公式可以求出运动的时间,结合速度公式可以求出刹车的时间,与学生运动时间比较可以判别小明可以乘上公车。
24.【答案】 (1)解;羚羊加速阶段需要时间 t1=x1v1=50m25m/s+02=4s
羚羊加速度 a1=v1t1=6.25m/s2
猎豹加速阶段需要时间 t2=x2v2=60m30m/s+02=4s
猎豹加速度 a2=v2t2=7.5m/s2
(2)解;猎豹在加速阶段运动距离为 x2=60m
而羚羊在这段时间内运动的距离为 x1=12a1(t1?1s)2=2258m
根据题意有 x2≥x1+x
即 x≤x2?x1=31.875m≈32m
(3)解;猎豹从开始攻击到开始减速运动的距离为 x′2=60m+30m/s×4s=180m 而羚羊在这段时间内的运动距离为 x′1=50m+25m/s×(4s?1s)=125m
根据题意有 x′2≥x′1+x′
即 x′≤x′2?x′1=180m?125m=55m
(4)解;当猎豹的速度减小到跟羚羊的速度相等时,如果还没追上羚羊,则最终不会追上了。这个过程猎豹减速的时间为 t=v2?v1a=2s
减速阶段,猎豹比羚羊多跑的距离为 Δx=(30+252×2?25×2)m=5m
根据题意有 x″≥x+Δx=60m
【解析】(1)羚羊和猎豹都做匀加速直线运动;利用平均速度公式可以求出加速的时间,结合速度公式可以求出加速度的大小;
(2)羚羊做匀加速直线运动,利用位移公式可以求出羚羊运动的位移,结合猎豹在加速段运动的位移大小可以求出两者的距离大小;
(3)猎豹先加速后运动运动,利用位移公式可以求出运动的距离;结合羚羊先加速后匀速运动的位移,可以求出两者之间的距离;
(4)当猎豹和羚羊的速度相等时,利用速度公式可以求出猎豹减速的时间,结合位移公式可以求出羚羊没被追上的距离大小。
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
