五年级下册数学教案-4.5 组合体的体积沪教版
文档属性
| 名称 | 五年级下册数学教案-4.5 组合体的体积沪教版 | 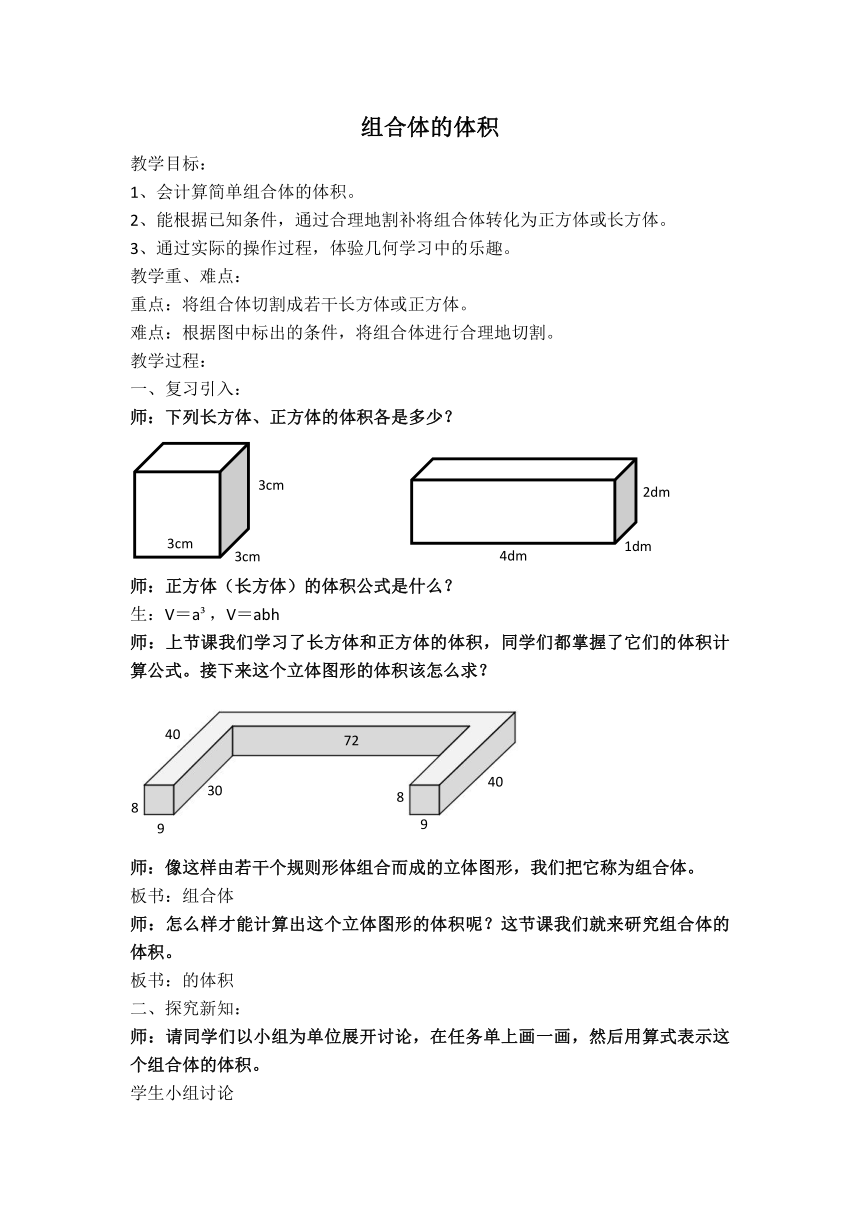 | |
| 格式 | doc | ||
| 文件大小 | 52.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-14 15:17:40 | ||
图片预览

文档简介
组合体的体积
教学目标:
会计算简单组合体的体积。
能根据已知条件,通过合理地割补将组合体转化为正方体或长方体。
通过实际的操作过程,体验几何学习中的乐趣。
教学重、难点:
重点:将组合体切割成若干长方体或正方体。
难点:根据图中标出的条件,将组合体进行合理地切割。
教学过程:
复习引入:
师:下列长方体、正方体的体积各是多少?
师:正方体(长方体)的体积公式是什么?
生:V=a?,V=abh
师:上节课我们学习了长方体和正方体的体积,同学们都掌握了它们的体积计算公式。接下来这个立体图形的体积该怎么求?
师:像这样由若干个规则形体组合而成的立体图形,我们把它称为组合体。
板书:组合体
师:怎么样才能计算出这个立体图形的体积呢?这节课我们就来研究组合体的体积。
板书:的体积
探究新知:
师:请同学们以小组为单位展开讨论,在任务单上画一画,然后用算式表示这个组合体的体积。
学生小组讨论
师:哪一小组来分享一下,你们是怎么求出这个组合体的体积的?
师:观察一下,这两个小组的方法有什么共同点?
生:都把这个组合体切割成了三个长方体。
师:你观察得很仔细,也就是说,他们通过“割”的方法,将组合体转化成了若干个长方体,分别计算体积后再相加,从而求出了组合体的体积。
板书:组合体→→割→→长方体(相加)
师:我们能够通过“割”的方法求出组合体的体积。同样是这个组合体,你们还有别的方法吗?再请一组来交流。
师:哪位同学来说一说,这一组是怎么求出组合体的体积的?
生:将这个组合体补成一个长方体,用大长方体的体积减小长方体的体积。
师:你描述地很具体。也就是说,他们通过“补”的方法,将组合体转化成了一个完整的长方体,分别求出补成的长方体和补进去的长方体的体积后再相减,得到了组合体的体积。
板书:组合体→→补→→长方体(相减)
师:谁能来说一说,刚才我们都用了什么方法求出组合体的体积?
生:我们用“割”和“补”的方法将组合体转化为长方体,经过相加或相减求出组合体的体积。
师:让我们用今天学到的新本领解决问题。
巩固练习:
1、用算式表示下面组合体的体积:
师:为什么同样的一个组合体,三个问题你们用了三种不同的方法来解答?
生:数据不同,方法不同。
师:可见,在计算组合体的体积是,我们需要根据已知的数据,选择合适的方法,通过合理地割补解决问题。
板书:根据数据,合理割补
师:如果老师只给出这些数据,你能求出这个组合体的体积吗?
V=Sh
师:看来,我们不仅可以用“割”或者“补”的方法求出组合体的体积,我们还可以利用底面积乘高的方法求出这类柱体的体积。
判断下列算法是否正确:
师:你还有其他想法吗?
用你喜欢的方法求出下面组合体的体积(单位:m):
教学目标:
会计算简单组合体的体积。
能根据已知条件,通过合理地割补将组合体转化为正方体或长方体。
通过实际的操作过程,体验几何学习中的乐趣。
教学重、难点:
重点:将组合体切割成若干长方体或正方体。
难点:根据图中标出的条件,将组合体进行合理地切割。
教学过程:
复习引入:
师:下列长方体、正方体的体积各是多少?
师:正方体(长方体)的体积公式是什么?
生:V=a?,V=abh
师:上节课我们学习了长方体和正方体的体积,同学们都掌握了它们的体积计算公式。接下来这个立体图形的体积该怎么求?
师:像这样由若干个规则形体组合而成的立体图形,我们把它称为组合体。
板书:组合体
师:怎么样才能计算出这个立体图形的体积呢?这节课我们就来研究组合体的体积。
板书:的体积
探究新知:
师:请同学们以小组为单位展开讨论,在任务单上画一画,然后用算式表示这个组合体的体积。
学生小组讨论
师:哪一小组来分享一下,你们是怎么求出这个组合体的体积的?
师:观察一下,这两个小组的方法有什么共同点?
生:都把这个组合体切割成了三个长方体。
师:你观察得很仔细,也就是说,他们通过“割”的方法,将组合体转化成了若干个长方体,分别计算体积后再相加,从而求出了组合体的体积。
板书:组合体→→割→→长方体(相加)
师:我们能够通过“割”的方法求出组合体的体积。同样是这个组合体,你们还有别的方法吗?再请一组来交流。
师:哪位同学来说一说,这一组是怎么求出组合体的体积的?
生:将这个组合体补成一个长方体,用大长方体的体积减小长方体的体积。
师:你描述地很具体。也就是说,他们通过“补”的方法,将组合体转化成了一个完整的长方体,分别求出补成的长方体和补进去的长方体的体积后再相减,得到了组合体的体积。
板书:组合体→→补→→长方体(相减)
师:谁能来说一说,刚才我们都用了什么方法求出组合体的体积?
生:我们用“割”和“补”的方法将组合体转化为长方体,经过相加或相减求出组合体的体积。
师:让我们用今天学到的新本领解决问题。
巩固练习:
1、用算式表示下面组合体的体积:
师:为什么同样的一个组合体,三个问题你们用了三种不同的方法来解答?
生:数据不同,方法不同。
师:可见,在计算组合体的体积是,我们需要根据已知的数据,选择合适的方法,通过合理地割补解决问题。
板书:根据数据,合理割补
师:如果老师只给出这些数据,你能求出这个组合体的体积吗?
V=Sh
师:看来,我们不仅可以用“割”或者“补”的方法求出组合体的体积,我们还可以利用底面积乘高的方法求出这类柱体的体积。
判断下列算法是否正确:
师:你还有其他想法吗?
用你喜欢的方法求出下面组合体的体积(单位:m):
