7.1.2弧度制及其与角度制的换算-【新教材】人教B版(2019)高中数学必修第三册课时练习(Word含解析)
文档属性
| 名称 | 7.1.2弧度制及其与角度制的换算-【新教材】人教B版(2019)高中数学必修第三册课时练习(Word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 393.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 00:00:00 | ||
图片预览




文档简介
7.1.2弧度制及其与角度制的换算课时练习
A级 巩固基础
一、单选题
1.圆心角弧度数和半径均为2的扇形的弧长为( )
A.1 B.2 C.4 D.8
2.已知扇形的圆心角为,面积为,则扇形的半径为( )
A. B. C. D.
3.已知一扇形的面积为圆心角为60°,则该扇形的弧长为( ).
A. B. C.π D.
4.给出下列3个结论,其中正确的个数是( )
①是第三象限角;②是第二象限角;③.
A.3 B.2 C.1 D.0
5.3弧度的角终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.下列叙述中,正确的是( )
A.1弧度是1度的圆心角所对的弧
B.1弧度是长度为半径的弧
C.1弧度是1度的弧与1度的角的和
D.1弧度是长度等于半径的弧所对的圆心角,它是角的一种度量单位
7.将转化为弧度为( )
A. B. C. D.
8.下列转化结果正确的是( )
A.化成弧度是 B.化成角度是
C.化成弧度是 D.化成角度是
B级 综合应用
二、填空题
9.是第__象限角.
10.已知圆的半径为2,则的圆心角所对的弧长为______.
11.若扇形的弧长为4,圆心角为2,则其半径为______.
12.在直径长为的圆中,圆心角为时所对的弧长为________.
三、解答题
13.把下列弧度化成角度:(1);(2);(3).
14.把下列角度化成弧度:(1);(2);(3).
C级 拓展探究
15.已知扇形的圆心角为,.
(1)求扇形的弧长;
(2)求图中阴影部分的面积.
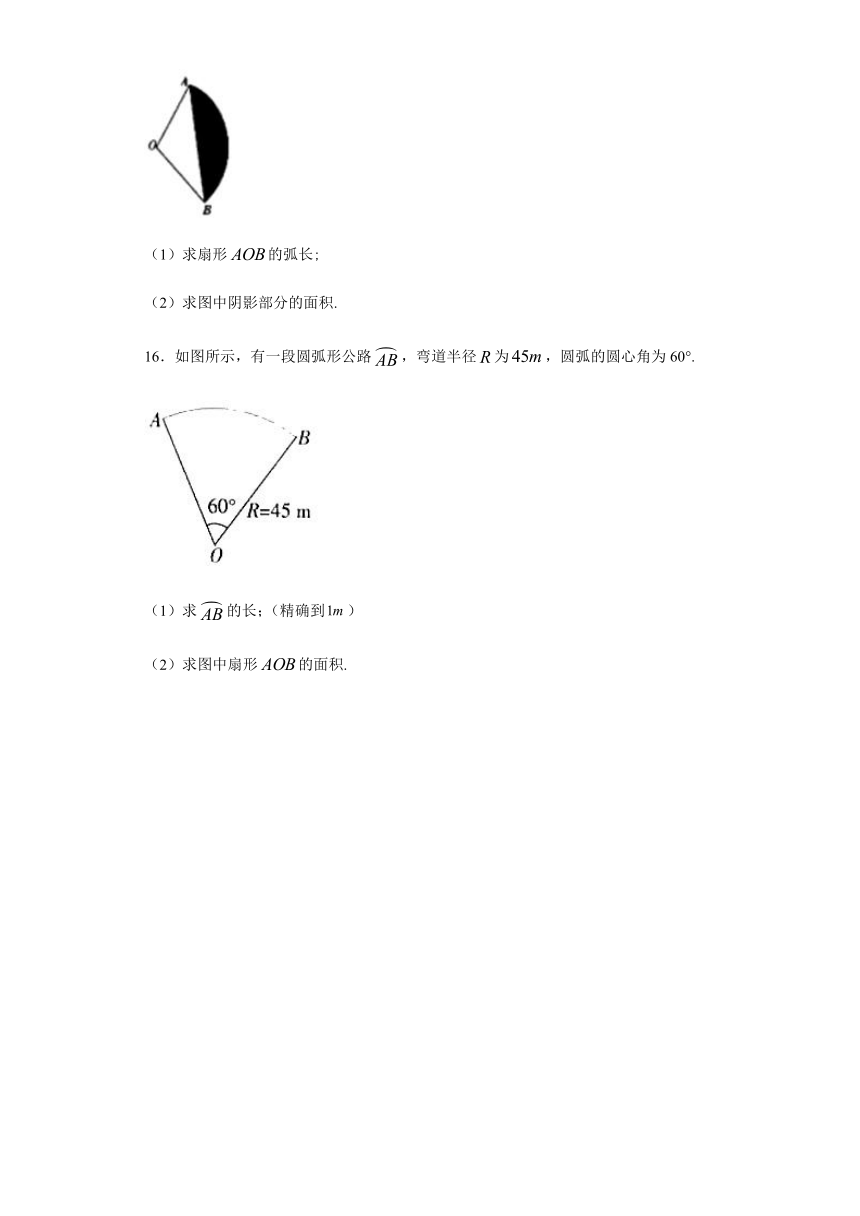
16.如图所示,有一段圆弧形公路,弯道半径为,圆弧的圆心角为60°.
(1)求的长;(精确到)
(2)求图中扇形的面积.
参考答案
1.C
【分析】
利用弧长公式求解.
【详解】
因为,
所以,
故选:C
2.C
【分析】
利用扇形的面积公式即可求解.
【详解】
设扇形的半径为,则扇形的面积,
解得:,
故选:C
3.B
【分析】
由扇形面积公式求R,应用弧长公式即可求弧长.
【详解】
令扇形的半径为R,由扇形面积为,可得,
∴扇形的弧长为,
故选:B
4.C
【分析】
根据象限角的定义,以及角度制和弧度制互化公式,判断选项
【详解】
①,所以是第三象限角,正确;②,所以是第三象限角,故不正确;③,故不正确.
故选:C
5.B
【分析】
可得,即可得出.
【详解】
因为,所以3弧度的角终边在第二象限.
故选:B.
6.D
【分析】
根据弧度的定义即可判断.
【详解】
根据弧度的定义,在单位圆中,长度为1的弧所对的圆心角称为1弧度角.
故选:D.
7.D
【分析】
将角度转化为弧度只需将角度的数值乘以即可;
【详解】
解:
故选:D
8.D
【分析】
根据弧度制与角度制的转化关系,可得选项.
【详解】
由得,对于A选项:化成弧度是,故A不正确;
对于B选项:化成角度是,故B不正确;
对于C选项:化成弧度是,故C错误;
对于D选项:化成角度是,故D正确,
故选:D.
9.三
【分析】
在找到与其终边相同的角即可判断.
【详解】
,
而是第三象限角,是第三象限角.
故答案为:三.
10.
【分析】
由已知结合弧长公式即可直接求解.
【详解】
由弧长公式可得.
故答案为:
【点睛】
本小题主要考查弧长公式,属于基础题.
11.2
【分析】
利用扇形的弧长公式即可得出.
【详解】
解:由弧长公式可得,解得.
故答案为:2.
【点睛】
本题考查了扇形的弧长公式,属于基础题.
12.
【分析】
将角度使用弧度数表示,然后根据弧长公式计算可得结果.
【详解】
∵,
∴弧长.
故答案为:
【点睛】
本题考查弧长公式,掌握公式,简单计算,属基础题.
13.1);(2);(3).
【分析】
(1)利用转化即可
(2) 利用转化即可
(3) 利用转化即可
【详解】
(1).
(2).
(3).
【点睛】
本题考查的是角度制和弧度制的相互转化,较简单.
14.(1);(2);(3).
【分析】
(1)利用转化即可
(2) 利用转化即可
(3) 利用转化即可
【详解】
(1).
(2).
(3).
【点睛】
本题考查的是角度制和弧度制的相互转化,较简单.
15.(1);(2)
【分析】
根据图象,作于,则.再由扇形的圆心角为,
得出,则,有弧长公式可得.
(2)由(1)可得,扇形的半径为,弧长为,利用扇形面积公式求出扇形面积,再求出的面积,相减即得阴影部分的面积.
【详解】
解:(1)如图,作于,则.
因为扇形的圆心角为,
所以,则,
故扇形的弧长.
(2)由(1)可得,扇形的半径为,
弧长为,则扇形的面积为
的面积为,
故图中阴影部分的面积为.
【点睛】
本题考查弧长公式和扇形面积公式,是基础题.
16.(1);(2).
【分析】
(1)根据扇形的弧长公式,可得到答案;.
(2)根据扇形的面积公式,可得到答案.
【详解】
(1)根据扇形的弧长公式,可得.
(2)根据扇形的面积公式,可得.
【点睛】
本题考查了扇形中的弧长公式,考查了扇形的面积公式,属于基础题.
A级 巩固基础
一、单选题
1.圆心角弧度数和半径均为2的扇形的弧长为( )
A.1 B.2 C.4 D.8
2.已知扇形的圆心角为,面积为,则扇形的半径为( )
A. B. C. D.
3.已知一扇形的面积为圆心角为60°,则该扇形的弧长为( ).
A. B. C.π D.
4.给出下列3个结论,其中正确的个数是( )
①是第三象限角;②是第二象限角;③.
A.3 B.2 C.1 D.0
5.3弧度的角终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.下列叙述中,正确的是( )
A.1弧度是1度的圆心角所对的弧
B.1弧度是长度为半径的弧
C.1弧度是1度的弧与1度的角的和
D.1弧度是长度等于半径的弧所对的圆心角,它是角的一种度量单位
7.将转化为弧度为( )
A. B. C. D.
8.下列转化结果正确的是( )
A.化成弧度是 B.化成角度是
C.化成弧度是 D.化成角度是
B级 综合应用
二、填空题
9.是第__象限角.
10.已知圆的半径为2,则的圆心角所对的弧长为______.
11.若扇形的弧长为4,圆心角为2,则其半径为______.
12.在直径长为的圆中,圆心角为时所对的弧长为________.
三、解答题
13.把下列弧度化成角度:(1);(2);(3).
14.把下列角度化成弧度:(1);(2);(3).
C级 拓展探究
15.已知扇形的圆心角为,.
(1)求扇形的弧长;
(2)求图中阴影部分的面积.
16.如图所示,有一段圆弧形公路,弯道半径为,圆弧的圆心角为60°.
(1)求的长;(精确到)
(2)求图中扇形的面积.
参考答案
1.C
【分析】
利用弧长公式求解.
【详解】
因为,
所以,
故选:C
2.C
【分析】
利用扇形的面积公式即可求解.
【详解】
设扇形的半径为,则扇形的面积,
解得:,
故选:C
3.B
【分析】
由扇形面积公式求R,应用弧长公式即可求弧长.
【详解】
令扇形的半径为R,由扇形面积为,可得,
∴扇形的弧长为,
故选:B
4.C
【分析】
根据象限角的定义,以及角度制和弧度制互化公式,判断选项
【详解】
①,所以是第三象限角,正确;②,所以是第三象限角,故不正确;③,故不正确.
故选:C
5.B
【分析】
可得,即可得出.
【详解】
因为,所以3弧度的角终边在第二象限.
故选:B.
6.D
【分析】
根据弧度的定义即可判断.
【详解】
根据弧度的定义,在单位圆中,长度为1的弧所对的圆心角称为1弧度角.
故选:D.
7.D
【分析】
将角度转化为弧度只需将角度的数值乘以即可;
【详解】
解:
故选:D
8.D
【分析】
根据弧度制与角度制的转化关系,可得选项.
【详解】
由得,对于A选项:化成弧度是,故A不正确;
对于B选项:化成角度是,故B不正确;
对于C选项:化成弧度是,故C错误;
对于D选项:化成角度是,故D正确,
故选:D.
9.三
【分析】
在找到与其终边相同的角即可判断.
【详解】
,
而是第三象限角,是第三象限角.
故答案为:三.
10.
【分析】
由已知结合弧长公式即可直接求解.
【详解】
由弧长公式可得.
故答案为:
【点睛】
本小题主要考查弧长公式,属于基础题.
11.2
【分析】
利用扇形的弧长公式即可得出.
【详解】
解:由弧长公式可得,解得.
故答案为:2.
【点睛】
本题考查了扇形的弧长公式,属于基础题.
12.
【分析】
将角度使用弧度数表示,然后根据弧长公式计算可得结果.
【详解】
∵,
∴弧长.
故答案为:
【点睛】
本题考查弧长公式,掌握公式,简单计算,属基础题.
13.1);(2);(3).
【分析】
(1)利用转化即可
(2) 利用转化即可
(3) 利用转化即可
【详解】
(1).
(2).
(3).
【点睛】
本题考查的是角度制和弧度制的相互转化,较简单.
14.(1);(2);(3).
【分析】
(1)利用转化即可
(2) 利用转化即可
(3) 利用转化即可
【详解】
(1).
(2).
(3).
【点睛】
本题考查的是角度制和弧度制的相互转化,较简单.
15.(1);(2)
【分析】
根据图象,作于,则.再由扇形的圆心角为,
得出,则,有弧长公式可得.
(2)由(1)可得,扇形的半径为,弧长为,利用扇形面积公式求出扇形面积,再求出的面积,相减即得阴影部分的面积.
【详解】
解:(1)如图,作于,则.
因为扇形的圆心角为,
所以,则,
故扇形的弧长.
(2)由(1)可得,扇形的半径为,
弧长为,则扇形的面积为
的面积为,
故图中阴影部分的面积为.
【点睛】
本题考查弧长公式和扇形面积公式,是基础题.
16.(1);(2).
【分析】
(1)根据扇形的弧长公式,可得到答案;.
(2)根据扇形的面积公式,可得到答案.
【详解】
(1)根据扇形的弧长公式,可得.
(2)根据扇形的面积公式,可得.
【点睛】
本题考查了扇形中的弧长公式,考查了扇形的面积公式,属于基础题.
