7.3.2正弦型函数的性质与图像-【新教材】人教B版(2019)高中数学必修第三册课时练习(Word含解析)
文档属性
| 名称 | 7.3.2正弦型函数的性质与图像-【新教材】人教B版(2019)高中数学必修第三册课时练习(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 843.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 15:34:04 | ||
图片预览

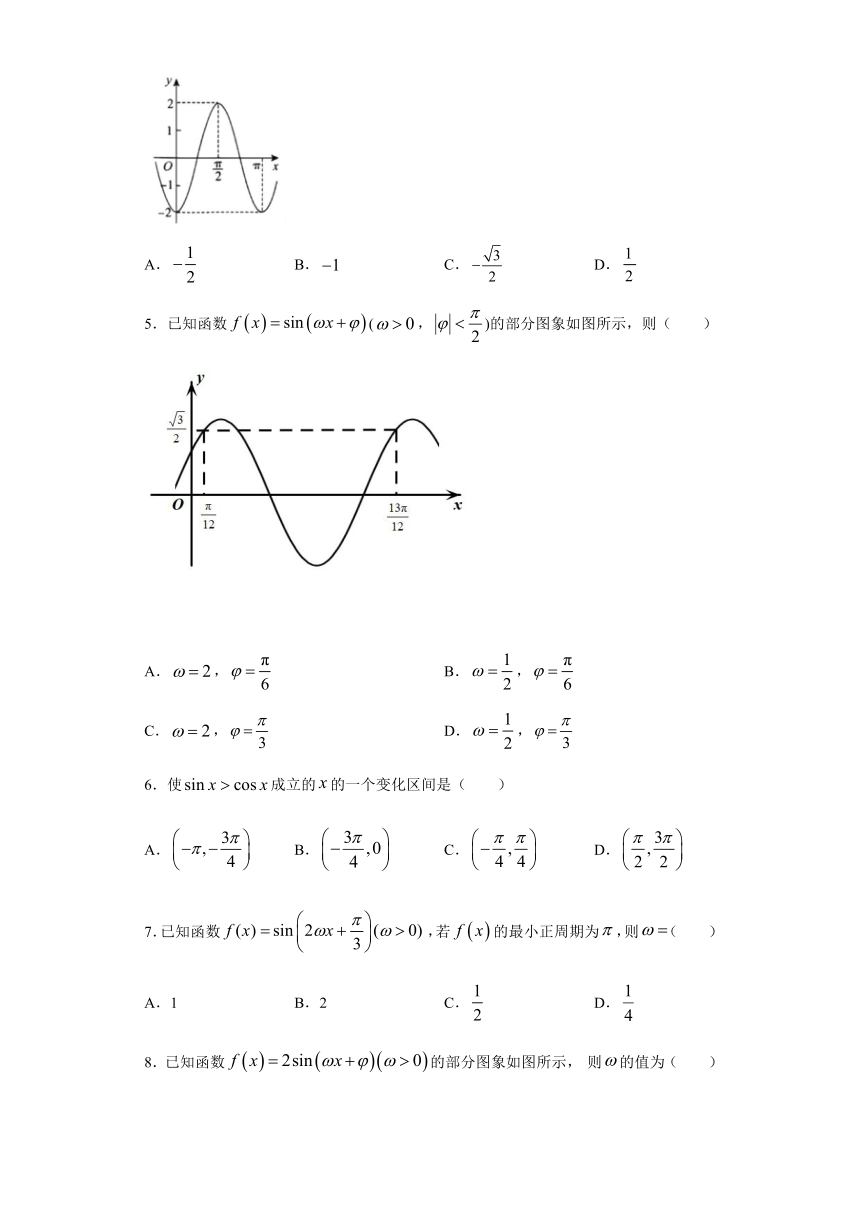


文档简介
7.3.2正弦型函数的性质与图像课时练习
A级 巩固基础
一、单选题
1.函数的最小正周期为( )
A. B. C. D.
2.关于函数的图象向右平移个单位长度后得到图象,则函数( )
A.最大值为3 B.最小正周期为
C.为奇函数 D.图象关于轴对称
3.已知函数最小正周期为,其图象的一条对称轴是,则此函数的解析式可以是( )
A. B.
C. D.
4.如图是函数的部分图象,则( )
A. B. C. D.
5.已知函数(,)的部分图象如图所示,则( )
A., B.,
C., D.,
6.使成立的的一个变化区间是( )
A. B. C. D.
7.已知函数,若的最小正周期为,则( )
A.1 B.2 C. D.
8.已知函数的部分图象如图所示, 则的值为( )
A.1 B. C. D.2
B级 综合应用
9.函数的单调递增区间是( )
A.,
B.,
C.,
D.,
10.函数的部分图像如图所示,则该函数的解析式为( )
A. B.
C. D.
二、填空题
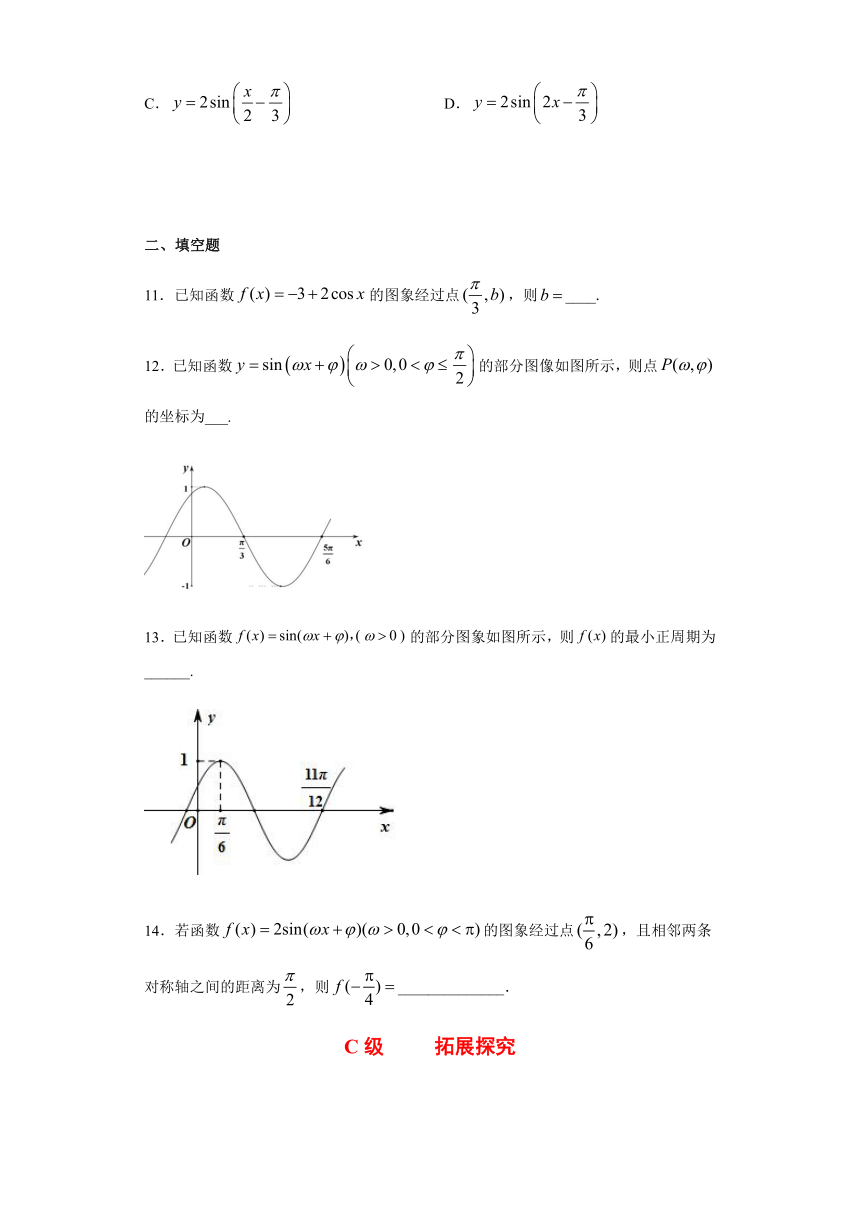
11.已知函数的图象经过点,则____.
12.已知函数的部分图像如图所示,则点的坐标为___.
13.已知函数的部分图象如图所示,则的最小正周期为______.
14.若函数的图象经过点,且相邻两条对称轴之间的距离为,则______________.
C级 拓展探究
三、解答题
15.已知函数的部分图象如图所示.
(1)求的解析式.
(2)写出的递增区间.
16.已知函数.
(1)在给定的坐标系中,作出函数在区间上的图象;
(2)求函数在区间上的最大值和最小值.
参考答案
1.C
【解析】
由题意,故选C.
【名师点睛】函数的性质:
(1).
(2)最小正周期
(3)由求对称轴.
(4)由求增区间;由求减区间.
2.D
【分析】
先根据图象的平移变换和诱导公式得,再根据的解析式可得答案.
【详解】
依题意可得,
所以的最大值为4,最小正周期为,为偶函数,图象关于轴对称.
故选:D
【点睛】
本题考查了函数图像的平移变换,考查了诱导公式,考查了函数的最值,周期性和奇偶性,属于基础题.
3.A
【分析】
使用排除法,根据正弦型三角函数的最小周期为,可排除D,然后根据当时,函数取最值,可得结果.
【详解】
因为函数的最小正周期是,
故先排除选项D;
又对于选项B:,
对于选项C:,
故B、C均被排除,应选A.
故选:A
【点睛】
本题考查正弦型函数的周期性以及对称性,主要掌握以及函数在对称轴上取最值,考验计算能力,属基础题.
4.B
【分析】
根据三角函数的图像求出解析式,将代入解析式即可求解.
【详解】
解析:由图可知.最小正周期,∴,
又由,得,
∴,
即.
故选:B
【点睛】
本题考查了由三角函数的图像求解析式、求特殊角的三角函数值,属于基础题.
5.A
【分析】
先根据函数图象得到周期求出,然后带特殊点求值即可.
【详解】
解:由题图可知函数的周期,则,
则,
将代入解析式中得,
则,或,,
解得,或,,
因为,则.
故选:A
【点睛】
本题主要考查三角函数的图象和性质求函数解析式,考查数形结合思想,是基础题.
6.A
【分析】
先化简已知得,再解不等式即得解.
【详解】
由题得.
所以
当时,
因为.
故选:
【点睛】
本题主要考查三角恒等变换,考查三角函数的图象和性质,意在考查学生对这些知识的理解掌握水平.
7.A
【分析】
根据最小正周期的公式求解即可.
【详解】
由题,.
故选:A
【点睛】
本题主要考查了正弦型函数的最小正周期,属于基础题.
8.D
【分析】
由题设可得,由公式可求得.
【详解】
由题设可得,所以周期,
则,
故选:D.
【点睛】
本题考查由的部分图象确定其解析式,理解三角函数图象的特征是解题的关键,属于中档题.
9.D
【分析】
根据正弦函数的单调性,并采用整体法,可得结果.
【详解】
由
令
所以
函数的单调递增区间为,
故选:D
【点睛】
本题考查正弦型函数的单调递增区间,重点在于把握正弦函数的单调性,同时对于整体法的应用,使问题化繁为简,属基础题.
10.A
【分析】
根据图象求出即可得到函数解析式.
【详解】
显然,
因为,所以,所以,
由得,
所以,即,,
因为,所以,
所以.
故选:A
【点睛】
本题考查了根据图象求函数解析式,利用周期求,代入最高点的坐标求是解题关键,属于基础题.
11.-2
【分析】
根据三角函数的图象和性质,直接代入即可得到结论.
【详解】
∵函数的图象经过点,
∴b=f()=3+2cos3+23+1=,
故答案为.
【点睛】
本题主要考查三角函数的图象和性质,比较基础.
12.
【分析】
先利用周期算出,再代入点即可》
【详解】
由题意,可得,即,所以,即,
由函数经过点且为单调递减区间的零点,所以,解得,又由,所以,
故答案为:.
【点晴】
此题考根据函数图像求解析式,属于简单题.
13.
【分析】
观察图象,可列式,解得结果即可.
【详解】
设的最小正周期为,
由图可知,,解得.
故答案为:.
【点睛】
本题考查了由三角函数的图象求最小正周期,属于基础题.
14.
【分析】
根据对称轴之间距离求出最小正周期,从而求得;再将点代入函数解析式,结合的取值范围,可求出的值,求出函数的解析式,即可求出的值.
【详解】
因为相邻两条对称轴之间的距离为,所以,
解得,所以.
因为函数的图象经过点,所以,
所以,即,因为,所以,
所以,所以.
故答案为:.
【点睛】
本题考查利用三角函数图像特点求解解析式,关键在于能够通过对称轴之间距离求出的最小正周期,属于基础题.
15.(1);(2),.
【分析】
(1)由图可知,,再将点代入得,可得,,从而可求出答案;
(2)解出,即可得答案.
【详解】
解:(1)易知,,
∴,
∴,
将点代入得,
,,
∴,,
∵,
∴,
∴;
(2)由,,
解得,,
∴的递增区间为,.
【点睛】
本题主要考查根据三角函数的图象确定解析式,考查三角函数的图象与性质,属于基础题.
16.(1)作图见解析(2)最大值为;最小值为
【分析】
(1)列表、建系、画图;
(2)求出相位的取值范围,根据函数的单调性,求最值.
【详解】
(1).
列表如下:
0
1 0
0
1
描点、连线得在上的图象,如图所示.
(2)由(1),得.
当,即,
∴当,即时,取得最大值为;
当,即时,取得最小值为.
【点睛】
本题考查了“五点法”作图,三角函数性质的运用,属于基础题.
A级 巩固基础
一、单选题
1.函数的最小正周期为( )
A. B. C. D.
2.关于函数的图象向右平移个单位长度后得到图象,则函数( )
A.最大值为3 B.最小正周期为
C.为奇函数 D.图象关于轴对称
3.已知函数最小正周期为,其图象的一条对称轴是,则此函数的解析式可以是( )
A. B.
C. D.
4.如图是函数的部分图象,则( )
A. B. C. D.
5.已知函数(,)的部分图象如图所示,则( )
A., B.,
C., D.,
6.使成立的的一个变化区间是( )
A. B. C. D.
7.已知函数,若的最小正周期为,则( )
A.1 B.2 C. D.
8.已知函数的部分图象如图所示, 则的值为( )
A.1 B. C. D.2
B级 综合应用
9.函数的单调递增区间是( )
A.,
B.,
C.,
D.,
10.函数的部分图像如图所示,则该函数的解析式为( )
A. B.
C. D.
二、填空题
11.已知函数的图象经过点,则____.
12.已知函数的部分图像如图所示,则点的坐标为___.
13.已知函数的部分图象如图所示,则的最小正周期为______.
14.若函数的图象经过点,且相邻两条对称轴之间的距离为,则______________.
C级 拓展探究
三、解答题
15.已知函数的部分图象如图所示.
(1)求的解析式.
(2)写出的递增区间.
16.已知函数.
(1)在给定的坐标系中,作出函数在区间上的图象;
(2)求函数在区间上的最大值和最小值.
参考答案
1.C
【解析】
由题意,故选C.
【名师点睛】函数的性质:
(1).
(2)最小正周期
(3)由求对称轴.
(4)由求增区间;由求减区间.
2.D
【分析】
先根据图象的平移变换和诱导公式得,再根据的解析式可得答案.
【详解】
依题意可得,
所以的最大值为4,最小正周期为,为偶函数,图象关于轴对称.
故选:D
【点睛】
本题考查了函数图像的平移变换,考查了诱导公式,考查了函数的最值,周期性和奇偶性,属于基础题.
3.A
【分析】
使用排除法,根据正弦型三角函数的最小周期为,可排除D,然后根据当时,函数取最值,可得结果.
【详解】
因为函数的最小正周期是,
故先排除选项D;
又对于选项B:,
对于选项C:,
故B、C均被排除,应选A.
故选:A
【点睛】
本题考查正弦型函数的周期性以及对称性,主要掌握以及函数在对称轴上取最值,考验计算能力,属基础题.
4.B
【分析】
根据三角函数的图像求出解析式,将代入解析式即可求解.
【详解】
解析:由图可知.最小正周期,∴,
又由,得,
∴,
即.
故选:B
【点睛】
本题考查了由三角函数的图像求解析式、求特殊角的三角函数值,属于基础题.
5.A
【分析】
先根据函数图象得到周期求出,然后带特殊点求值即可.
【详解】
解:由题图可知函数的周期,则,
则,
将代入解析式中得,
则,或,,
解得,或,,
因为,则.
故选:A
【点睛】
本题主要考查三角函数的图象和性质求函数解析式,考查数形结合思想,是基础题.
6.A
【分析】
先化简已知得,再解不等式即得解.
【详解】
由题得.
所以
当时,
因为.
故选:
【点睛】
本题主要考查三角恒等变换,考查三角函数的图象和性质,意在考查学生对这些知识的理解掌握水平.
7.A
【分析】
根据最小正周期的公式求解即可.
【详解】
由题,.
故选:A
【点睛】
本题主要考查了正弦型函数的最小正周期,属于基础题.
8.D
【分析】
由题设可得,由公式可求得.
【详解】
由题设可得,所以周期,
则,
故选:D.
【点睛】
本题考查由的部分图象确定其解析式,理解三角函数图象的特征是解题的关键,属于中档题.
9.D
【分析】
根据正弦函数的单调性,并采用整体法,可得结果.
【详解】
由
令
所以
函数的单调递增区间为,
故选:D
【点睛】
本题考查正弦型函数的单调递增区间,重点在于把握正弦函数的单调性,同时对于整体法的应用,使问题化繁为简,属基础题.
10.A
【分析】
根据图象求出即可得到函数解析式.
【详解】
显然,
因为,所以,所以,
由得,
所以,即,,
因为,所以,
所以.
故选:A
【点睛】
本题考查了根据图象求函数解析式,利用周期求,代入最高点的坐标求是解题关键,属于基础题.
11.-2
【分析】
根据三角函数的图象和性质,直接代入即可得到结论.
【详解】
∵函数的图象经过点,
∴b=f()=3+2cos3+23+1=,
故答案为.
【点睛】
本题主要考查三角函数的图象和性质,比较基础.
12.
【分析】
先利用周期算出,再代入点即可》
【详解】
由题意,可得,即,所以,即,
由函数经过点且为单调递减区间的零点,所以,解得,又由,所以,
故答案为:.
【点晴】
此题考根据函数图像求解析式,属于简单题.
13.
【分析】
观察图象,可列式,解得结果即可.
【详解】
设的最小正周期为,
由图可知,,解得.
故答案为:.
【点睛】
本题考查了由三角函数的图象求最小正周期,属于基础题.
14.
【分析】
根据对称轴之间距离求出最小正周期,从而求得;再将点代入函数解析式,结合的取值范围,可求出的值,求出函数的解析式,即可求出的值.
【详解】
因为相邻两条对称轴之间的距离为,所以,
解得,所以.
因为函数的图象经过点,所以,
所以,即,因为,所以,
所以,所以.
故答案为:.
【点睛】
本题考查利用三角函数图像特点求解解析式,关键在于能够通过对称轴之间距离求出的最小正周期,属于基础题.
15.(1);(2),.
【分析】
(1)由图可知,,再将点代入得,可得,,从而可求出答案;
(2)解出,即可得答案.
【详解】
解:(1)易知,,
∴,
∴,
将点代入得,
,,
∴,,
∵,
∴,
∴;
(2)由,,
解得,,
∴的递增区间为,.
【点睛】
本题主要考查根据三角函数的图象确定解析式,考查三角函数的图象与性质,属于基础题.
16.(1)作图见解析(2)最大值为;最小值为
【分析】
(1)列表、建系、画图;
(2)求出相位的取值范围,根据函数的单调性,求最值.
【详解】
(1).
列表如下:
0
1 0
0
1
描点、连线得在上的图象,如图所示.
(2)由(1),得.
当,即,
∴当,即时,取得最大值为;
当,即时,取得最小值为.
【点睛】
本题考查了“五点法”作图,三角函数性质的运用,属于基础题.
