湖北省十堰东风国际高级中学2020-2021学年高一下学期期末数学模拟卷2 Word版含答案
文档属性
| 名称 | 湖北省十堰东风国际高级中学2020-2021学年高一下学期期末数学模拟卷2 Word版含答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 428.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 00:00:00 | ||
图片预览


文档简介
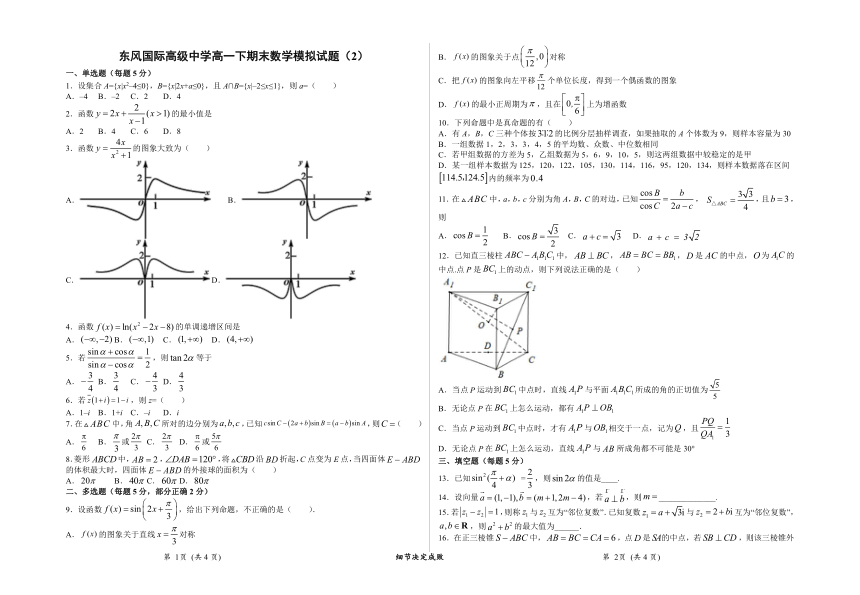
东风国际高级中学1131570011861800高一下期末数学模拟试题(2)
一、单选题(每题5分)
1.设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a=( )
A.–4 B.–2 C.2 D.4
2.函数false的最小值是
A.2 B.4 C.6 D.8
3.函数false的图象大致为( )
A. B.
C. D.
4.函数false的单调递增区间是
A.false B.false C.false D.false
5.若false,则false等于
A.false B.false C.false D.false
6.若false,则z=( )
A.1–i B.1+i C.–i D.i
7.在false中,角false所对的边分别为false,已知false,则false( )
A.false B.false或false C.false D.false或false
8.菱形false中,false,false,将false沿false折起,C点变为E点,当四面体false的体积最大时,四面体false的外接球的面积为( )
A.false B.false C.false D.false
二、多选题(每题5分,部分正确2分)
9.设函数false,给出下列命题,不正确的是( ).
A.false的图象关于直线false对称
B.false的图象关于点false对称
C.把false的图象向左平移false个单位长度,得到一个偶函数的图象
D.false的最小正周期为false,且在false上为增函数
10.下列命题中是真命题的有( )
A.有A,B,C三种个体按false的比例分层抽样调查,如果抽取的A个体数为9,则样本容量为30
B.一组数据1,2,3,3,4,5的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是甲
D.某一组样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在区间false内的频率为false
11.在false中,a,b,c分别为角A,B,C的对边,已知false, false,且false,则
A.false B.false C.false D.false
12.已知直三棱柱false中,false,false,false是false的中点,false为false的中点.点false是false上的动点,则下列说法正确的是( )
A.当点false运动到false中点时,直线false与平面false所成的角的正切值为false
B.无论点false在false上怎么运动,都有false
C.当点false运动到false中点时,才有false与false相交于一点,记为false,且false
D.无论点false在false上怎么运动,直线false与false所成角都不可能是30°
三、填空题(每题5分)
13.已知false =false,则false的值是____.
14.设向量false,若false,则false______________.
15.若false,则称false与false互为“邻位复数”.已知复数false与false互为“邻位复数”, false,则false的最大值为______.
16.在正三棱锥false中,false,点false是false的中点,若false,则该三棱锥外接球的表面积为___________.
四、解答题(共70分,其中17题10分,18-22题每题12分)
17.为了落实习主席提出“绿水青山就是金山银山”的环境治理要求,某市政府积极鼓励居民节约用水.计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准false(吨),一位居民的月用水量不超过false的部分按平价收费,超出false的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年200位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2),…,[8,9)分成9组,制成了如图所示的频率分布直方图,其中false.
(1)求直方图中false的值,并由频率分布直方图估计该市居民用水的平均数(每组数据用该组区间中点值作为代表);
(2)设该市有40万居民,估计全市居民中月均用水量不低于2吨的人数,并说明理由;
(3)若该市政府希望使85%的居民每月的用水量不超过标准false(吨),估计false的值,并说明理由.
18.在false中,false,false,false分别为角false,false,false的对边,且false.
(1)求角false;
(2)若false的面积为false,false边上的高false,求false,false.
19.已知函数false(false,,false)的图象如下图所示
(1)求出函数false的解析式;
(2)若将函数false的图象向右移动false个单位长度再把所有点的横坐标变为原来的false(纵坐标不变)得到函数false的图象,求出函数false的单调增区间及对称中心.
20.如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧面PAD是正三角形,侧面false底面ABCD,M是PD的中点.
(1)求证:false平面PCD;
(2)求侧面PBC与底面ABCD所成二面角的余弦值.
21.在锐角false中,角false的对边分别为false,已知false
(1)若false,求false;
(2)求false的取值范围.
22.已知函数false.
(Ⅰ)若false,求函数false的定义域和值域;
(Ⅱ)若函数false的定义域为false,值域为false,求实数false的值.
1200150011163300期末模拟试卷(2)参考答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
A
D
B
D
C
A
ABD
BD
AD
ABD
13.false 14.5 15. 16..
1.B 求解二次不等式可得:,解一次不等式可得:.,故:,解得:.
2.C 因为,
所以,
取等号时,即,所以.
3.A由函数的解析式可得:,则函数为奇函数,其图象关于坐标原点对称,选项CD错误;当时,,选项B错误.
4.D由>0得:x∈(?∞,?2)∪(4,+∞),
令t=,则y=lnt,∵x∈(?∞,?2)时,t=为减函数;
x∈(4,+∞)时,t=为增函数;y=lnt为增函数,
故函数f(x)=ln()的单调递增区间是(4,+∞),
5.B ,false.
6.D因为,所以.
7.C依题意,由正弦定理得,
,false,false,
即.由于,所以.
8.A由题意,三棱锥false的底面的面积为定值,当平面平面时,此时点到底面的距离最大,此时三棱锥false的体积取得最大值,
因为四边形为菱形,且,连接交与点,
可得,所以为的外心,
过点作平面的垂线,可得上点到三点的距离相等,
设存在点点,使得,即点为三棱锥false的外接球的球心,
设false,可得,
即,解得,所以外接球的半径为,
所以外接球的表面积为.
9.ABD因为,所以A不正确;因为,所以B不正确;
因为函数的最小正周期为,但,所以D不正确;把函数的图象向左平移个单位长度,得到函数的图象,函数为偶函数,所以C正确.
10.BD对于选项A:根据样本的抽样比等于各层的抽样比,样本容量为,故选项A 不正确;对于选项B:数据1,2,3,3,4,5的平均数为,众数和中位数都是,故选项B正确;对于选项C:乙组数据的平均数为,乙组数据的方差为,所以这两组数据中较稳定的是乙,故选项C不正确;对于选项D:样本数据落在区间有120,122,116,120有个,所以样本数据落在区间内的频率为,故选项D,
11.AD false.
整理可得:
可得 false
为三角形内角, false 故A正确,B错误.
false
false 解得 ,
由余弦定理得 false
解得, 故C错误,D正确.
12.ABD直三棱柱中,,
选项A中,当点运动到false中点时,如图1所示,有E为false的中点,连接、,即有面∴直线与平面所成的角的正切值:
∵,∴,故A正确
选项B中,连接false,与false交于E,并连接,如图2所示
由题意知,为正方形,即有
而且为直三棱柱,有面,面
∴,又∴面false,面false,故
同理可证:,又∴面,又面,即有,故B正确 选项C中,点运动到false中点时,如图3所示,即在△false中、均为中位线
∴Q为中位线的交点∴根据中位线的性质有:,故C错误
选项D中,由于,直线与所成角即为与所成角:
结合图4分析知:点在false上运动时 当在或上时,最大为45°
当在false中点时,最小为∴不可能是30°,D正确
图1 图2 图3 图4
13.false
故答案为:false
14.5 由可得,又因为,
所以,即,故答案为:5.
15. 因为复数与互为“邻位复数”,所以,故,其表示的是点在圆上,而表示点到原点的距离,故的最大值为原点到圆心的距离加半径,即.故答案为:
16. 设的中心为,连接,,∴平面,面,∴,
又,,∴平面,平面,∴,
又false,,∴平面. 平面,,
∵为正三棱锥,∴,,两两垂直,,
353695044450外接球直径为,
三棱锥外接球表面积.
故答案为:.
17.(1),;4.07(2)35.2万;(3)
解:(1)由频率分布直方图可得
,
又,则,,
该市居民用水的平均数估计为:
;
(2)由频率分布直方图可得,月均用水量不超过2吨的频率为:,
则月均用水量不低于2吨的频率为:,所以全市40万居民中月均用水量不低于2吨的人数为:(万);
(3)由频率分布直方图知月均用水量不超过6吨的频率为:0.88,
月均用水量不超过5吨的频率为0.73,则85%的居民每月的用水量不超过的标准(吨),,
,解得,即标准为5.8吨.
18.(1);(2),.
解:(1)因为,所以,
所以,即false.
由余弦定理可得,因为,所以.
(2)由正弦定理可得.
因为的面积为,所以,解得.
由余弦定理可得,则.
19.(1);(2),.
(1) 由图可得
且而, 故
综上
(2)显然 由得
的单调递增区间为.. 由.
20.(1)见解析;(2)false
(1)在正方形ABCD中,,
又侧面底面ABCD,侧面底面,所以平面PAD,
false平面PAD,所以,是正三角形,M是PD的中点,所以,
又,所以平面PCD.
(2)取AD,BC的中点分别为E,F,连接EF,PE,PF,
则,所以,
又在正中,,平面PEF,
∵正方形ABCD中,平面PEF,
是侧面PBC与底面ABCD所成二面角的平面角,
由平面PAD,,平面PEF,平面PAD,
.设正方形ABCD的边长,则,
所以,所以,
即侧面PBC与底面ABCD所成二面角的余弦值为false.
21.(1);(2).
(1)由,得,得,得,在,,由余弦定理,得,
即,解得或.当时, 即为钝角(舍),
故符合.
(2)由(1)得,所以,
,
为锐角三角形,,,,
,故的取值范围是.
22.(Ⅰ)定义域为,值域为;(Ⅱ).
(Ⅰ)若,则,由,得到
,得到,故定义域为.
令,则 当时,符合.
当时,上述方程要有解,则,得到或,
又,所以,所以,则值域为.
(Ⅱ)由于函数的定义域为,则恒成立,则,即,令,由于的值域为,则,而
,则由解得 ,故和是方程即的两个根,则,得到,符合题意.所以.
一、单选题(每题5分)
1.设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a=( )
A.–4 B.–2 C.2 D.4
2.函数false的最小值是
A.2 B.4 C.6 D.8
3.函数false的图象大致为( )
A. B.
C. D.
4.函数false的单调递增区间是
A.false B.false C.false D.false
5.若false,则false等于
A.false B.false C.false D.false
6.若false,则z=( )
A.1–i B.1+i C.–i D.i
7.在false中,角false所对的边分别为false,已知false,则false( )
A.false B.false或false C.false D.false或false
8.菱形false中,false,false,将false沿false折起,C点变为E点,当四面体false的体积最大时,四面体false的外接球的面积为( )
A.false B.false C.false D.false
二、多选题(每题5分,部分正确2分)
9.设函数false,给出下列命题,不正确的是( ).
A.false的图象关于直线false对称
B.false的图象关于点false对称
C.把false的图象向左平移false个单位长度,得到一个偶函数的图象
D.false的最小正周期为false,且在false上为增函数
10.下列命题中是真命题的有( )
A.有A,B,C三种个体按false的比例分层抽样调查,如果抽取的A个体数为9,则样本容量为30
B.一组数据1,2,3,3,4,5的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是甲
D.某一组样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在区间false内的频率为false
11.在false中,a,b,c分别为角A,B,C的对边,已知false, false,且false,则
A.false B.false C.false D.false
12.已知直三棱柱false中,false,false,false是false的中点,false为false的中点.点false是false上的动点,则下列说法正确的是( )
A.当点false运动到false中点时,直线false与平面false所成的角的正切值为false
B.无论点false在false上怎么运动,都有false
C.当点false运动到false中点时,才有false与false相交于一点,记为false,且false
D.无论点false在false上怎么运动,直线false与false所成角都不可能是30°
三、填空题(每题5分)
13.已知false =false,则false的值是____.
14.设向量false,若false,则false______________.
15.若false,则称false与false互为“邻位复数”.已知复数false与false互为“邻位复数”, false,则false的最大值为______.
16.在正三棱锥false中,false,点false是false的中点,若false,则该三棱锥外接球的表面积为___________.
四、解答题(共70分,其中17题10分,18-22题每题12分)
17.为了落实习主席提出“绿水青山就是金山银山”的环境治理要求,某市政府积极鼓励居民节约用水.计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准false(吨),一位居民的月用水量不超过false的部分按平价收费,超出false的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年200位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2),…,[8,9)分成9组,制成了如图所示的频率分布直方图,其中false.
(1)求直方图中false的值,并由频率分布直方图估计该市居民用水的平均数(每组数据用该组区间中点值作为代表);
(2)设该市有40万居民,估计全市居民中月均用水量不低于2吨的人数,并说明理由;
(3)若该市政府希望使85%的居民每月的用水量不超过标准false(吨),估计false的值,并说明理由.
18.在false中,false,false,false分别为角false,false,false的对边,且false.
(1)求角false;
(2)若false的面积为false,false边上的高false,求false,false.
19.已知函数false(false,,false)的图象如下图所示
(1)求出函数false的解析式;
(2)若将函数false的图象向右移动false个单位长度再把所有点的横坐标变为原来的false(纵坐标不变)得到函数false的图象,求出函数false的单调增区间及对称中心.
20.如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧面PAD是正三角形,侧面false底面ABCD,M是PD的中点.
(1)求证:false平面PCD;
(2)求侧面PBC与底面ABCD所成二面角的余弦值.
21.在锐角false中,角false的对边分别为false,已知false
(1)若false,求false;
(2)求false的取值范围.
22.已知函数false.
(Ⅰ)若false,求函数false的定义域和值域;
(Ⅱ)若函数false的定义域为false,值域为false,求实数false的值.
1200150011163300期末模拟试卷(2)参考答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
A
D
B
D
C
A
ABD
BD
AD
ABD
13.false 14.5 15. 16..
1.B 求解二次不等式可得:,解一次不等式可得:.,故:,解得:.
2.C 因为,
所以,
取等号时,即,所以.
3.A由函数的解析式可得:,则函数为奇函数,其图象关于坐标原点对称,选项CD错误;当时,,选项B错误.
4.D由>0得:x∈(?∞,?2)∪(4,+∞),
令t=,则y=lnt,∵x∈(?∞,?2)时,t=为减函数;
x∈(4,+∞)时,t=为增函数;y=lnt为增函数,
故函数f(x)=ln()的单调递增区间是(4,+∞),
5.B ,false.
6.D因为,所以.
7.C依题意,由正弦定理得,
,false,false,
即.由于,所以.
8.A由题意,三棱锥false的底面的面积为定值,当平面平面时,此时点到底面的距离最大,此时三棱锥false的体积取得最大值,
因为四边形为菱形,且,连接交与点,
可得,所以为的外心,
过点作平面的垂线,可得上点到三点的距离相等,
设存在点点,使得,即点为三棱锥false的外接球的球心,
设false,可得,
即,解得,所以外接球的半径为,
所以外接球的表面积为.
9.ABD因为,所以A不正确;因为,所以B不正确;
因为函数的最小正周期为,但,所以D不正确;把函数的图象向左平移个单位长度,得到函数的图象,函数为偶函数,所以C正确.
10.BD对于选项A:根据样本的抽样比等于各层的抽样比,样本容量为,故选项A 不正确;对于选项B:数据1,2,3,3,4,5的平均数为,众数和中位数都是,故选项B正确;对于选项C:乙组数据的平均数为,乙组数据的方差为,所以这两组数据中较稳定的是乙,故选项C不正确;对于选项D:样本数据落在区间有120,122,116,120有个,所以样本数据落在区间内的频率为,故选项D,
11.AD false.
整理可得:
可得 false
为三角形内角, false 故A正确,B错误.
false
false 解得 ,
由余弦定理得 false
解得, 故C错误,D正确.
12.ABD直三棱柱中,,
选项A中,当点运动到false中点时,如图1所示,有E为false的中点,连接、,即有面∴直线与平面所成的角的正切值:
∵,∴,故A正确
选项B中,连接false,与false交于E,并连接,如图2所示
由题意知,为正方形,即有
而且为直三棱柱,有面,面
∴,又∴面false,面false,故
同理可证:,又∴面,又面,即有,故B正确 选项C中,点运动到false中点时,如图3所示,即在△false中、均为中位线
∴Q为中位线的交点∴根据中位线的性质有:,故C错误
选项D中,由于,直线与所成角即为与所成角:
结合图4分析知:点在false上运动时 当在或上时,最大为45°
当在false中点时,最小为∴不可能是30°,D正确
图1 图2 图3 图4
13.false
故答案为:false
14.5 由可得,又因为,
所以,即,故答案为:5.
15. 因为复数与互为“邻位复数”,所以,故,其表示的是点在圆上,而表示点到原点的距离,故的最大值为原点到圆心的距离加半径,即.故答案为:
16. 设的中心为,连接,,∴平面,面,∴,
又,,∴平面,平面,∴,
又false,,∴平面. 平面,,
∵为正三棱锥,∴,,两两垂直,,
353695044450外接球直径为,
三棱锥外接球表面积.
故答案为:.
17.(1),;4.07(2)35.2万;(3)
解:(1)由频率分布直方图可得
,
又,则,,
该市居民用水的平均数估计为:
;
(2)由频率分布直方图可得,月均用水量不超过2吨的频率为:,
则月均用水量不低于2吨的频率为:,所以全市40万居民中月均用水量不低于2吨的人数为:(万);
(3)由频率分布直方图知月均用水量不超过6吨的频率为:0.88,
月均用水量不超过5吨的频率为0.73,则85%的居民每月的用水量不超过的标准(吨),,
,解得,即标准为5.8吨.
18.(1);(2),.
解:(1)因为,所以,
所以,即false.
由余弦定理可得,因为,所以.
(2)由正弦定理可得.
因为的面积为,所以,解得.
由余弦定理可得,则.
19.(1);(2),.
(1) 由图可得
且而, 故
综上
(2)显然 由得
的单调递增区间为.. 由.
20.(1)见解析;(2)false
(1)在正方形ABCD中,,
又侧面底面ABCD,侧面底面,所以平面PAD,
false平面PAD,所以,是正三角形,M是PD的中点,所以,
又,所以平面PCD.
(2)取AD,BC的中点分别为E,F,连接EF,PE,PF,
则,所以,
又在正中,,平面PEF,
∵正方形ABCD中,平面PEF,
是侧面PBC与底面ABCD所成二面角的平面角,
由平面PAD,,平面PEF,平面PAD,
.设正方形ABCD的边长,则,
所以,所以,
即侧面PBC与底面ABCD所成二面角的余弦值为false.
21.(1);(2).
(1)由,得,得,得,在,,由余弦定理,得,
即,解得或.当时, 即为钝角(舍),
故符合.
(2)由(1)得,所以,
,
为锐角三角形,,,,
,故的取值范围是.
22.(Ⅰ)定义域为,值域为;(Ⅱ).
(Ⅰ)若,则,由,得到
,得到,故定义域为.
令,则 当时,符合.
当时,上述方程要有解,则,得到或,
又,所以,所以,则值域为.
(Ⅱ)由于函数的定义域为,则恒成立,则,即,令,由于的值域为,则,而
,则由解得 ,故和是方程即的两个根,则,得到,符合题意.所以.
同课章节目录
