2020-2021学年人教版九年级数学下册 27.2.3 相似三角形应用举例 训练(word版含解析)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册 27.2.3 相似三角形应用举例 训练(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 342.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 00:00:00 | ||
图片预览

文档简介
27.2.3 相似三角形应用举例
【笔记】
1.数学建模的关键是把生活中的实际问题转化为数学问题,转化的方法之一是画数学示意图,在画图的过程中可以逐渐明确问题中各量的数量关系与位置关系,进而形成解题思路.
2.相似三角形的应用
(1)测量不能到达顶部的物体的高度,通常借助太阳光照射物体形成影子,根据同一时刻物高与影长成________或利用相似三角形来解决问题.
(2)求不能直接到达的两点间的距离,关键是构造__________,然后根据相似三角形的性质求出两点间的距离.
【训练】
1.如图,球从A处射出,经球台边挡板CD反射到B,已知AC=10cm,BD=15cm,CD=50cm,则点E距离点C(
)
A.40cm
B.30cm
C.20cm
D.10cm
第1题图
2.已知:如图,小明在打网球时,要使球恰好能打过而且落在离网5米的位置上(网球运行轨迹为直线),则球拍击球的高度h应为(
)
A.0.9m
B.1.8m
C.2.7m
D.6m
第2题图
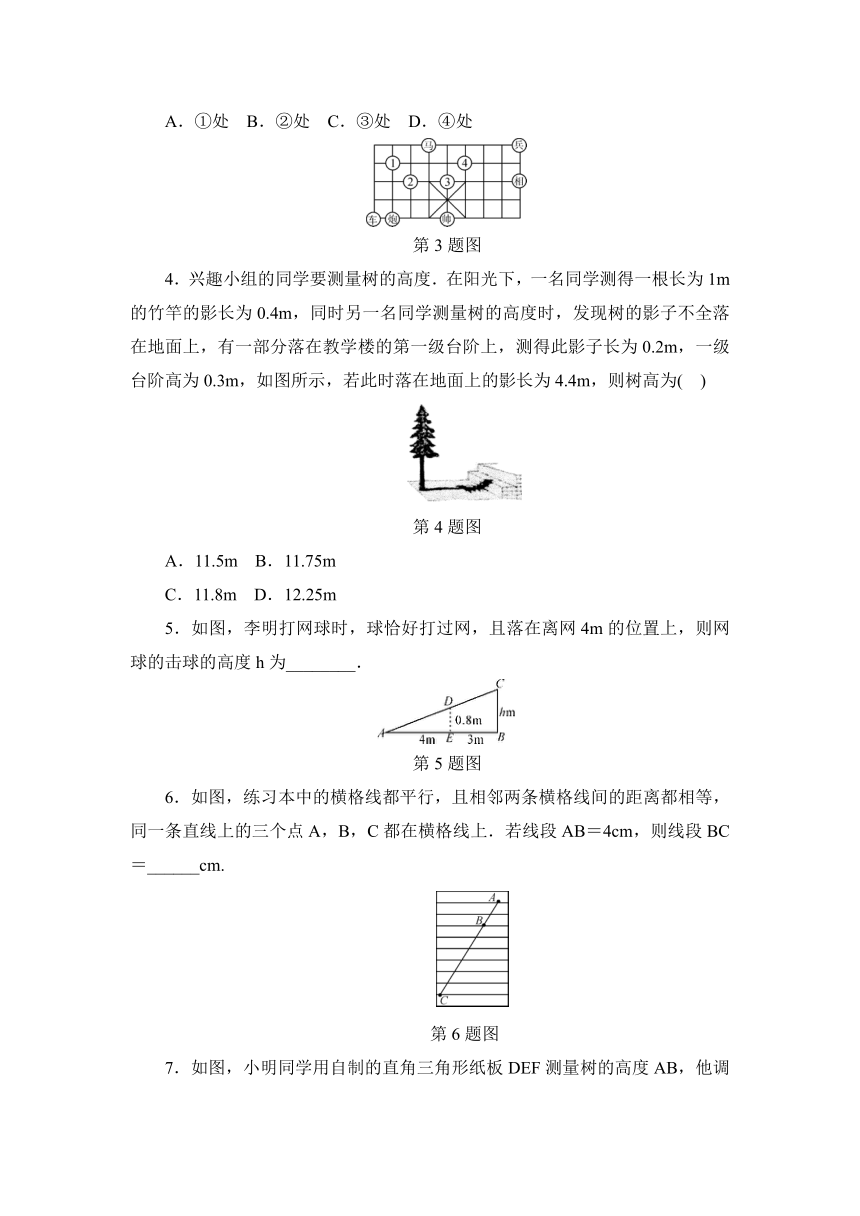
3.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似?(
)
A.①处
B.②处
C.③处
D.④处
第3题图
4.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1m的竹竿的影长为0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2m,一级台阶高为0.3m,如图所示,若此时落在地面上的影长为4.4m,则树高为(
)
第4题图
A.11.5m
B.11.75m
C.11.8m
D.12.25m
5.如图,李明打网球时,球恰好打过网,且落在离网4m的位置上,则网球的击球的高度h为________.
第5题图
6.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4cm,则线段BC=______cm.
第6题图
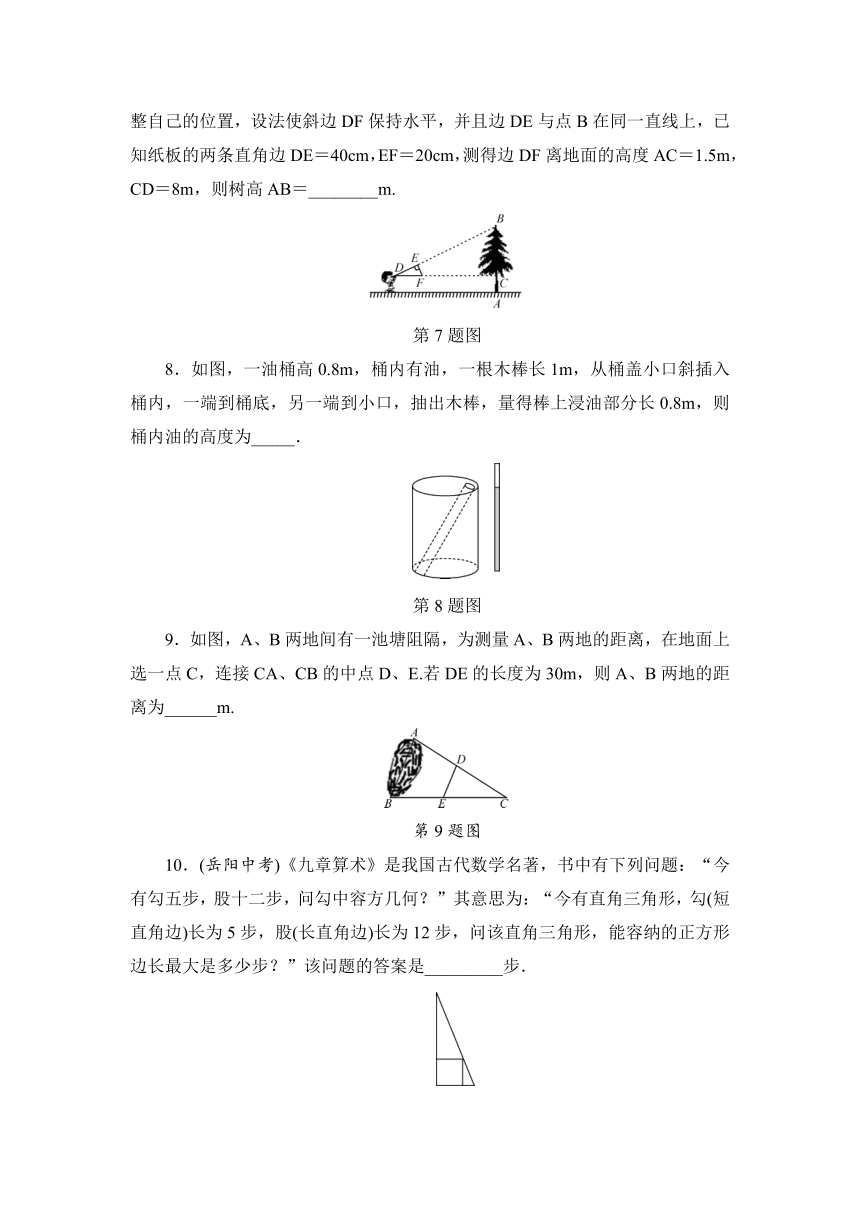
7.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=________m.
第7题图
8.如图,一油桶高0.8m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油的高度为_____.
第8题图
9.如图,A、B两地间有一池塘阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB的中点D、E.若DE的长度为30m,则A、B两地的距离为______m.
第9题图
10.(岳阳中考)《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形,能容纳的正方形边长最大是多少步?”该问题的答案是_________步.
第10题图
11.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为15cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点,若不考虑其他因素,求该台灯在桌面可照亮的宽度BD的长.
第11题图
12.如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为(
)
图1
图2
第12题图
A.
B.
C.
D.
13.有一支夹子如图所示,AB=2BC,BD=2BE,在夹子前面有一个长方体硬物,厚PQ为6cm,如果想用夹子的尖端A,D两点夹住P,Q两点,那么手握的地方EC至少要张开_______cm.
第13题图
14.如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C1处直立高3m的竹竿C1D1,然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合.小亮的眼睛离地面高度EF=E1F1=1.5m,量得CE=2m,EC1=6m,C1E1=3m.
第14题图
(1)由题意可知△FDM∽△________,△F1D1N∽△__________;
(2)求电线杆AB的高度.
15.如图所示,某小组发现8m高旗杆DE的影子EF落在了包含一圆弧形小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6m,测得其影长为2.4m,同时测得EG的长为3m,HF的长为1m,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2m,求小桥所在圆的半径.
第15题图
答案
【笔记】
2.(1)比例 (2)相似三角形
【训练】
1—4.CCBC 5.1.4m 6.12 7.5.5 8.0.64m 9.60 10.
11.∵AB⊥BD,AC⊥AB,∴AC∥BD,∴∠ACB=∠DBC,又∵∠A=∠BCD=90°,∴△ABC∽△CDB,∴=,∴BC2=AC·BD,在Rt△ABC中,BC2=AC2+AB2=152+302=1125,∴15BD=1125,∴BD=75(cm). 12.
A 13.3 14.(1)FBG F1BG (2)∵D1C1∥BA,∴△F1D1N∽△F1BG,∴=.∵DC∥BA,∴△FDM∽△FBG.∴=.∵D1N=DM,∴=,即=.∴GM=16.∵=,∴=.∴BG=13.5.∴AB=BG+GA=15(m).∴电线杆AB的高度为15m. 15.由相似得=,解得EF=12.∵EG=3,HF=1,∴GH=EF-EG-HF=8.由垂径定理得:GM=GH=4,又MN=2,设半径OG=r,则OM=r-2,又OM2+MG2=OG2,∴(r-2)2+42=r2,解得r=5.因此小桥所在圆的半径为5m.
【笔记】
1.数学建模的关键是把生活中的实际问题转化为数学问题,转化的方法之一是画数学示意图,在画图的过程中可以逐渐明确问题中各量的数量关系与位置关系,进而形成解题思路.
2.相似三角形的应用
(1)测量不能到达顶部的物体的高度,通常借助太阳光照射物体形成影子,根据同一时刻物高与影长成________或利用相似三角形来解决问题.
(2)求不能直接到达的两点间的距离,关键是构造__________,然后根据相似三角形的性质求出两点间的距离.
【训练】
1.如图,球从A处射出,经球台边挡板CD反射到B,已知AC=10cm,BD=15cm,CD=50cm,则点E距离点C(
)
A.40cm
B.30cm
C.20cm
D.10cm
第1题图
2.已知:如图,小明在打网球时,要使球恰好能打过而且落在离网5米的位置上(网球运行轨迹为直线),则球拍击球的高度h应为(
)
A.0.9m
B.1.8m
C.2.7m
D.6m
第2题图
3.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似?(
)
A.①处
B.②处
C.③处
D.④处
第3题图
4.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1m的竹竿的影长为0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2m,一级台阶高为0.3m,如图所示,若此时落在地面上的影长为4.4m,则树高为(
)
第4题图
A.11.5m
B.11.75m
C.11.8m
D.12.25m
5.如图,李明打网球时,球恰好打过网,且落在离网4m的位置上,则网球的击球的高度h为________.
第5题图
6.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4cm,则线段BC=______cm.
第6题图
7.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=________m.
第7题图
8.如图,一油桶高0.8m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油的高度为_____.
第8题图
9.如图,A、B两地间有一池塘阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB的中点D、E.若DE的长度为30m,则A、B两地的距离为______m.
第9题图
10.(岳阳中考)《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形,能容纳的正方形边长最大是多少步?”该问题的答案是_________步.
第10题图
11.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为15cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点,若不考虑其他因素,求该台灯在桌面可照亮的宽度BD的长.
第11题图
12.如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为(
)
图1
图2
第12题图
A.
B.
C.
D.
13.有一支夹子如图所示,AB=2BC,BD=2BE,在夹子前面有一个长方体硬物,厚PQ为6cm,如果想用夹子的尖端A,D两点夹住P,Q两点,那么手握的地方EC至少要张开_______cm.
第13题图
14.如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C1处直立高3m的竹竿C1D1,然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合.小亮的眼睛离地面高度EF=E1F1=1.5m,量得CE=2m,EC1=6m,C1E1=3m.
第14题图
(1)由题意可知△FDM∽△________,△F1D1N∽△__________;
(2)求电线杆AB的高度.
15.如图所示,某小组发现8m高旗杆DE的影子EF落在了包含一圆弧形小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6m,测得其影长为2.4m,同时测得EG的长为3m,HF的长为1m,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2m,求小桥所在圆的半径.
第15题图
答案
【笔记】
2.(1)比例 (2)相似三角形
【训练】
1—4.CCBC 5.1.4m 6.12 7.5.5 8.0.64m 9.60 10.
11.∵AB⊥BD,AC⊥AB,∴AC∥BD,∴∠ACB=∠DBC,又∵∠A=∠BCD=90°,∴△ABC∽△CDB,∴=,∴BC2=AC·BD,在Rt△ABC中,BC2=AC2+AB2=152+302=1125,∴15BD=1125,∴BD=75(cm). 12.
A 13.3 14.(1)FBG F1BG (2)∵D1C1∥BA,∴△F1D1N∽△F1BG,∴=.∵DC∥BA,∴△FDM∽△FBG.∴=.∵D1N=DM,∴=,即=.∴GM=16.∵=,∴=.∴BG=13.5.∴AB=BG+GA=15(m).∴电线杆AB的高度为15m. 15.由相似得=,解得EF=12.∵EG=3,HF=1,∴GH=EF-EG-HF=8.由垂径定理得:GM=GH=4,又MN=2,设半径OG=r,则OM=r-2,又OM2+MG2=OG2,∴(r-2)2+42=r2,解得r=5.因此小桥所在圆的半径为5m.
