第二十七章相似单元检测题 2020-2021学年人教版数学九年级下册(word版含答案)
文档属性
| 名称 | 第二十七章相似单元检测题 2020-2021学年人教版数学九年级下册(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1021.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 00:00:00 | ||
图片预览

文档简介
2020-2021学年度第二学期
九年级数学单元检测题(二)
(检测内容:第二十七章
相似)
考试时间:100分钟;满分:120分
班级:
姓名:
:考号
:分数
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列说法中,正确的是(
)
A.两个矩形必相似
B.两个含角的等腰三角形必相似
C.两个菱形必相似
D.两个含角的直角三角形必相似
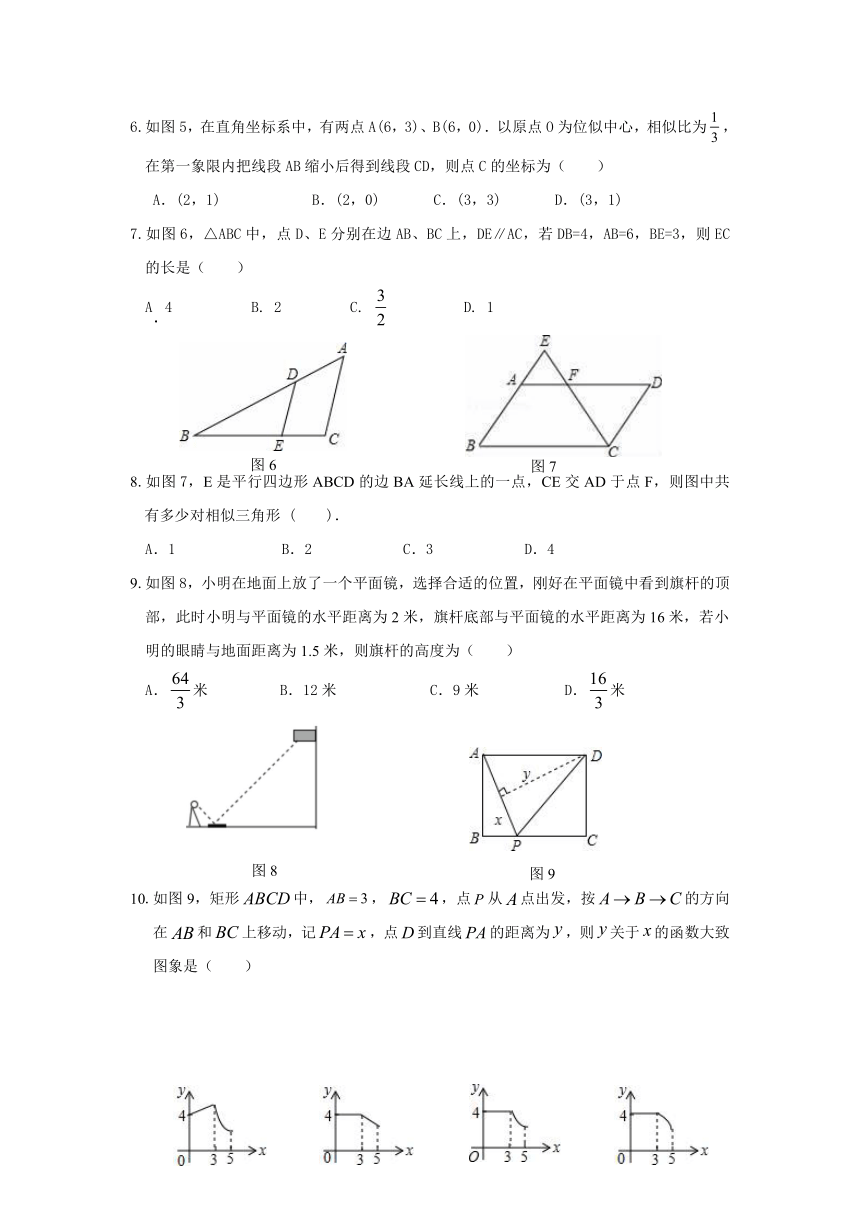
2.如图1的两个四边形相似,则∠α的度数是( )
A.87°
B.60°
C.75°
D.120°
3.如图2,直线a、b被三条互相平行的直线l1,l2,l3所截,AB=3,BC=2,则DE:DF=(
)
A.2:3
B.3:2
C.2:5
D.3:5
4.如图3,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
A.8
B.12
C.16
D.20
5.下列4×4正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与图4中△ABC相似的三角形所在的网格图形是( )
A
B
C
D
6.如图5,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(
)
A.(2,1)
B.(2,0)
C.(3,3)
D.(3,1)
7.如图6,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC的长是( )
A
4
B.
2
C.
D.
1
8.如图7,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,则图中共有多少对相似三角形
( ).
A.1
B.2
C.3
D.4[
9.如图8,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为16米,若小明的眼睛与地面距离为1.5米,则旗杆的高度为(
)
A.米
B.12米
C.9米
D.米
10.如图9,矩形中,,,点从点出发,按的方向在和上移动,记,点到直线的距离为,则关于的函数大致图象是(
)
网]
A
B
C
D
二、填空题(本大题共7小题,每小题4分,共28分)
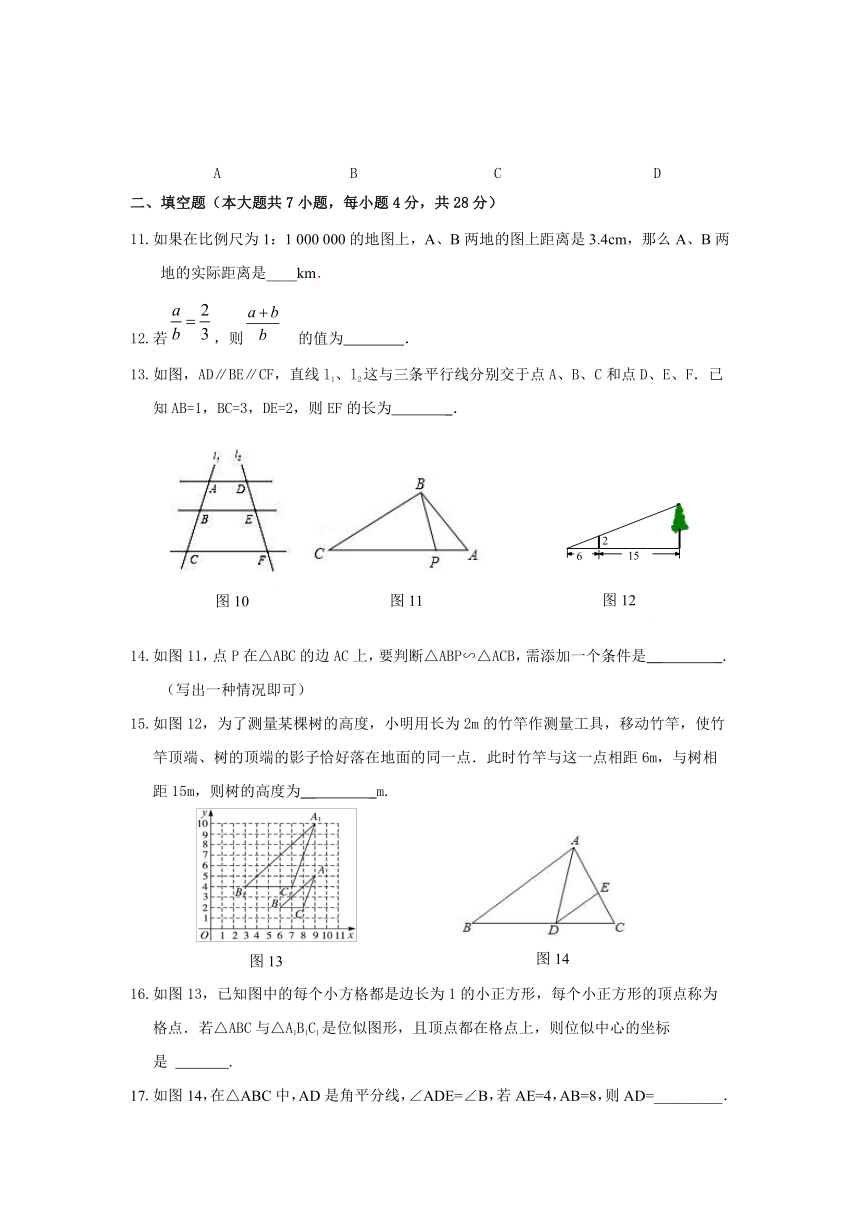
11.如果在比例尺为1:1
000
000的地图上,A、B两地的图上距离是3.4cm,那么A、B两地的实际距离是____km.
12.若,则
的值为
.
13.如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为
_.
14.如图11,点P在△ABC的边AC上,要判断△ABP∽△ACB,需添加一个条件是__
_.(写出一种情况即可)
15.如图12,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹
竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距6m,与树相
距15m,则树的高度为__
_m.
16.如图13,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为
格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标
是
.
17.如图14,在△ABC中,AD是角平分线,∠ADE=∠B,若AE=4,AB=8,则AD=_________.
三、解答题(本大题共3小题,每小题6分,共18分)
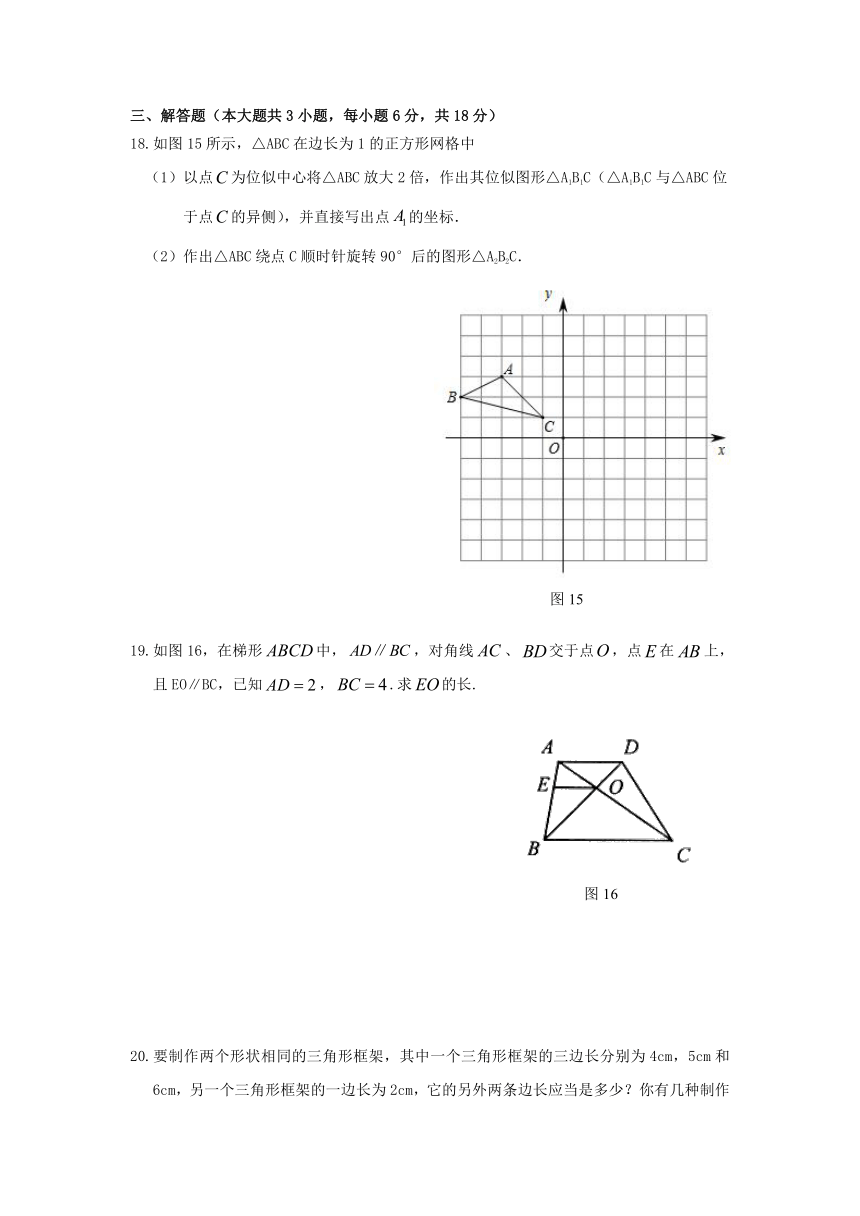
18.如图15所示,△ABC在边长为1的正方形网格中
(1)以点为位似中心将△ABC放大2倍,作出其位似图形△A1B1C(△A1B1C与△ABC位于点的异侧),并直接写出点的坐标.
(2)作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
19.如图16,在梯形中,,对角线、交于点,点在上,且EO∥BC,已知,.求的长.
20.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4cm,5cm和6cm,另一个三角形框架的一边长为2cm,它的另外两条边长应当是多少?你有几种制作方案?
四、解答题(本大题共3小题,每小题8分,共24分)
21.
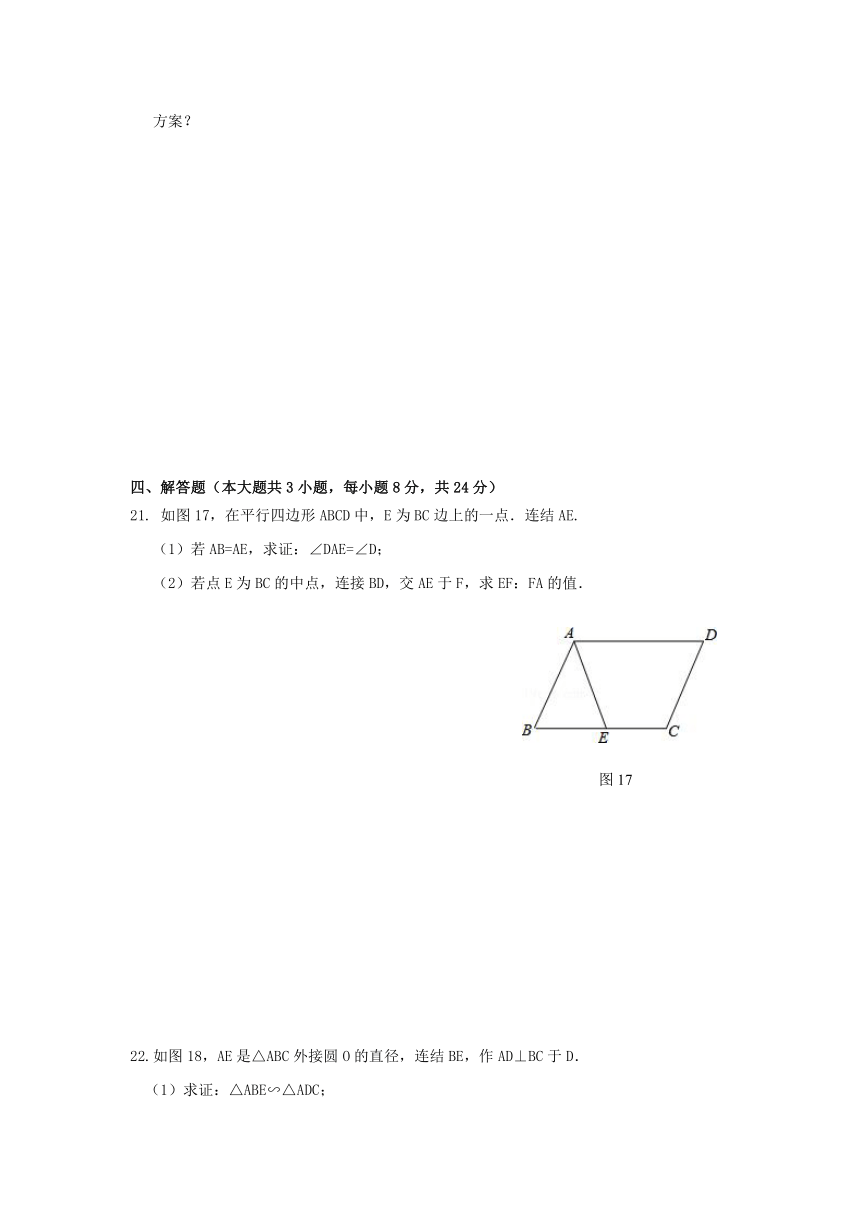
如图17,在平行四边形ABCD中,E为BC边上的一点.连结AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
22.如图18,AE是△ABC外接圆O的直径,连结BE,作AD⊥BC于D.
(1)求证:△ABE∽△ADC;
(2)若AB=8,AC=6,AE=10,求AD的长.
23.如图19,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由.
五、解答题(本大题共2小题,每小题10分,共20分)
24.如图20,在中,是的中点,且,,与相交于点,与相交于点.
(1)求证:;
(2)若,,求的面积.
25如图21,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.
(1)求证:BC平分∠PDB;
(2)求证:BC2=AB?BD;
(3)若PA=6,PC=6,求BD的长.
[来
2020-2021学年度第二学期
九年级数学单元检测题(二)
(检测内容:第二十七章
相似)
参考答案
选择题:(本大题共10小题,每小题3分,共30分)
1-5:
DADCD
6-10:ACCAC
二、填空题(本大题共7小题,每小题4分,共28分)
11.34
12.
13.
6
14.∠ABP=∠ACB.(不唯一)
15.
7
m.
16.
(9,0)
17.
4
三、解答题(本大题共3小题,第小题6分,共18分)
18.略
19.
EO=
20.略
四、解答题(本大题共3小题,第小题8分,共24分)
21.解:(1)在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠EAD,
∵AE=AB,
∴∠ABE=∠AEB,
∴∠B=∠EAD,
∵∠B=∠D,
∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,
∴
∵E为BC的中点,
∴BE=BC=AD
∴EF:FA=1:2.
22、
?解:(1)如图,∵AE是△ABC外接圆O的直径,且AD⊥BC,
∴∠ABE=∠ADC=90°
∵∠E=∠C,
∴△ABE∽△ADC.
(2)∵△ABE∽△ADC,
∴
而AB=8,AC=6,AE=10,
∴
∴AD=4.8.
23.解:设AP=2tcm,DQ=tcm,
∵AB=12cm,AD=6cm,
∴AQ=(6﹣t)cm,
∵∠A=∠A,
∴①当=时,△APQ∽△ABD,
∴=,
解得:t=3;
②当=时,△APQ∽△ADB,
∴=,
解得:t=1.2.
∴当t=3或1.2时,△APQ与△ABD相似.
五、解答题(本大题共2小题,第小题10分,共20分)
24.
(1)证明:∵,
∵且是的中点
∴
∴
∴
(2)解:过A作AH⊥CD,垂足为H.
∵AD=AC,
∴DH=CH,
∴BD:BH=2:3,
∵ED⊥BC,
∴ED∥AH,
∴△BDE∽△BHA,
∴ED:AH=BD:BH=2:3,
∵DE=3,
∴AH=,
∵△ABC∽△FCD,BC=2CD,
∴.
∵S△ABC=×BC×AH=×8×=18,
∴S△FCD=S△ABC=.
25.2解答:(1)证明:连接OC,
∵PD为圆O的切线,
∴OC⊥PD,
∵BD⊥PD,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBD=∠OBC,
则BC平分∠PBD;
(2)证明:连接AC,
∵AB为圆O的直径,
∴∠ACB=90°,
∵∠ACB=∠CDB=90°,∠ABC=∠CBD,
∴△ABC∽△CBD,
∴
即BC2=AB.BD;
(3)解:∵PC为圆O的切线,
∴OC⊥PD
∴∠PCA+∠ACO=900
∵AB为圆O的直径
∴∠ABC+BAC=900
∵OC=OA
∴∠OCA=∠OAC
∴∠PCA=∠ABC
∵∠P=∠P
∴△PAC∽△PCB
∴
∴PC2=PA.PB,
即72=6PB,
解得:PB=12,
∴AB=PB-PA=12-6=6,
∴OC=3,PO=PA+AO=9,
∵OC∥BD
∴
∴
则BD=4.
九年级数学单元检测题(二)
(检测内容:第二十七章
相似)
考试时间:100分钟;满分:120分
班级:
姓名:
:考号
:分数
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列说法中,正确的是(
)
A.两个矩形必相似
B.两个含角的等腰三角形必相似
C.两个菱形必相似
D.两个含角的直角三角形必相似
2.如图1的两个四边形相似,则∠α的度数是( )
A.87°
B.60°
C.75°
D.120°
3.如图2,直线a、b被三条互相平行的直线l1,l2,l3所截,AB=3,BC=2,则DE:DF=(
)
A.2:3
B.3:2
C.2:5
D.3:5
4.如图3,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
A.8
B.12
C.16
D.20
5.下列4×4正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与图4中△ABC相似的三角形所在的网格图形是( )
A
B
C
D
6.如图5,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(
)
A.(2,1)
B.(2,0)
C.(3,3)
D.(3,1)
7.如图6,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC的长是( )
A
4
B.
2
C.
D.
1
8.如图7,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,则图中共有多少对相似三角形
( ).
A.1
B.2
C.3
D.4[
9.如图8,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为16米,若小明的眼睛与地面距离为1.5米,则旗杆的高度为(
)
A.米
B.12米
C.9米
D.米
10.如图9,矩形中,,,点从点出发,按的方向在和上移动,记,点到直线的距离为,则关于的函数大致图象是(
)
网]
A
B
C
D
二、填空题(本大题共7小题,每小题4分,共28分)
11.如果在比例尺为1:1
000
000的地图上,A、B两地的图上距离是3.4cm,那么A、B两地的实际距离是____km.
12.若,则
的值为
.
13.如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为
_.
14.如图11,点P在△ABC的边AC上,要判断△ABP∽△ACB,需添加一个条件是__
_.(写出一种情况即可)
15.如图12,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹
竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距6m,与树相
距15m,则树的高度为__
_m.
16.如图13,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为
格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标
是
.
17.如图14,在△ABC中,AD是角平分线,∠ADE=∠B,若AE=4,AB=8,则AD=_________.
三、解答题(本大题共3小题,每小题6分,共18分)
18.如图15所示,△ABC在边长为1的正方形网格中
(1)以点为位似中心将△ABC放大2倍,作出其位似图形△A1B1C(△A1B1C与△ABC位于点的异侧),并直接写出点的坐标.
(2)作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
19.如图16,在梯形中,,对角线、交于点,点在上,且EO∥BC,已知,.求的长.
20.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4cm,5cm和6cm,另一个三角形框架的一边长为2cm,它的另外两条边长应当是多少?你有几种制作方案?
四、解答题(本大题共3小题,每小题8分,共24分)
21.
如图17,在平行四边形ABCD中,E为BC边上的一点.连结AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
22.如图18,AE是△ABC外接圆O的直径,连结BE,作AD⊥BC于D.
(1)求证:△ABE∽△ADC;
(2)若AB=8,AC=6,AE=10,求AD的长.
23.如图19,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由.
五、解答题(本大题共2小题,每小题10分,共20分)
24.如图20,在中,是的中点,且,,与相交于点,与相交于点.
(1)求证:;
(2)若,,求的面积.
25如图21,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.
(1)求证:BC平分∠PDB;
(2)求证:BC2=AB?BD;
(3)若PA=6,PC=6,求BD的长.
[来
2020-2021学年度第二学期
九年级数学单元检测题(二)
(检测内容:第二十七章
相似)
参考答案
选择题:(本大题共10小题,每小题3分,共30分)
1-5:
DADCD
6-10:ACCAC
二、填空题(本大题共7小题,每小题4分,共28分)
11.34
12.
13.
6
14.∠ABP=∠ACB.(不唯一)
15.
7
m.
16.
(9,0)
17.
4
三、解答题(本大题共3小题,第小题6分,共18分)
18.略
19.
EO=
20.略
四、解答题(本大题共3小题,第小题8分,共24分)
21.解:(1)在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠EAD,
∵AE=AB,
∴∠ABE=∠AEB,
∴∠B=∠EAD,
∵∠B=∠D,
∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,
∴
∵E为BC的中点,
∴BE=BC=AD
∴EF:FA=1:2.
22、
?解:(1)如图,∵AE是△ABC外接圆O的直径,且AD⊥BC,
∴∠ABE=∠ADC=90°
∵∠E=∠C,
∴△ABE∽△ADC.
(2)∵△ABE∽△ADC,
∴
而AB=8,AC=6,AE=10,
∴
∴AD=4.8.
23.解:设AP=2tcm,DQ=tcm,
∵AB=12cm,AD=6cm,
∴AQ=(6﹣t)cm,
∵∠A=∠A,
∴①当=时,△APQ∽△ABD,
∴=,
解得:t=3;
②当=时,△APQ∽△ADB,
∴=,
解得:t=1.2.
∴当t=3或1.2时,△APQ与△ABD相似.
五、解答题(本大题共2小题,第小题10分,共20分)
24.
(1)证明:∵,
∵且是的中点
∴
∴
∴
(2)解:过A作AH⊥CD,垂足为H.
∵AD=AC,
∴DH=CH,
∴BD:BH=2:3,
∵ED⊥BC,
∴ED∥AH,
∴△BDE∽△BHA,
∴ED:AH=BD:BH=2:3,
∵DE=3,
∴AH=,
∵△ABC∽△FCD,BC=2CD,
∴.
∵S△ABC=×BC×AH=×8×=18,
∴S△FCD=S△ABC=.
25.2解答:(1)证明:连接OC,
∵PD为圆O的切线,
∴OC⊥PD,
∵BD⊥PD,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBD=∠OBC,
则BC平分∠PBD;
(2)证明:连接AC,
∵AB为圆O的直径,
∴∠ACB=90°,
∵∠ACB=∠CDB=90°,∠ABC=∠CBD,
∴△ABC∽△CBD,
∴
即BC2=AB.BD;
(3)解:∵PC为圆O的切线,
∴OC⊥PD
∴∠PCA+∠ACO=900
∵AB为圆O的直径
∴∠ABC+BAC=900
∵OC=OA
∴∠OCA=∠OAC
∴∠PCA=∠ABC
∵∠P=∠P
∴△PAC∽△PCB
∴
∴PC2=PA.PB,
即72=6PB,
解得:PB=12,
∴AB=PB-PA=12-6=6,
∴OC=3,PO=PA+AO=9,
∵OC∥BD
∴
∴
则BD=4.
