2020-2021学年华东师大版数学七年级下册9.1.2三角形的内角和与外角和课后练习(word版含答案)
文档属性
| 名称 | 2020-2021学年华东师大版数学七年级下册9.1.2三角形的内角和与外角和课后练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 08:30:00 | ||
图片预览




文档简介
9.1.2三角形的内角和与外角和
一、单选题
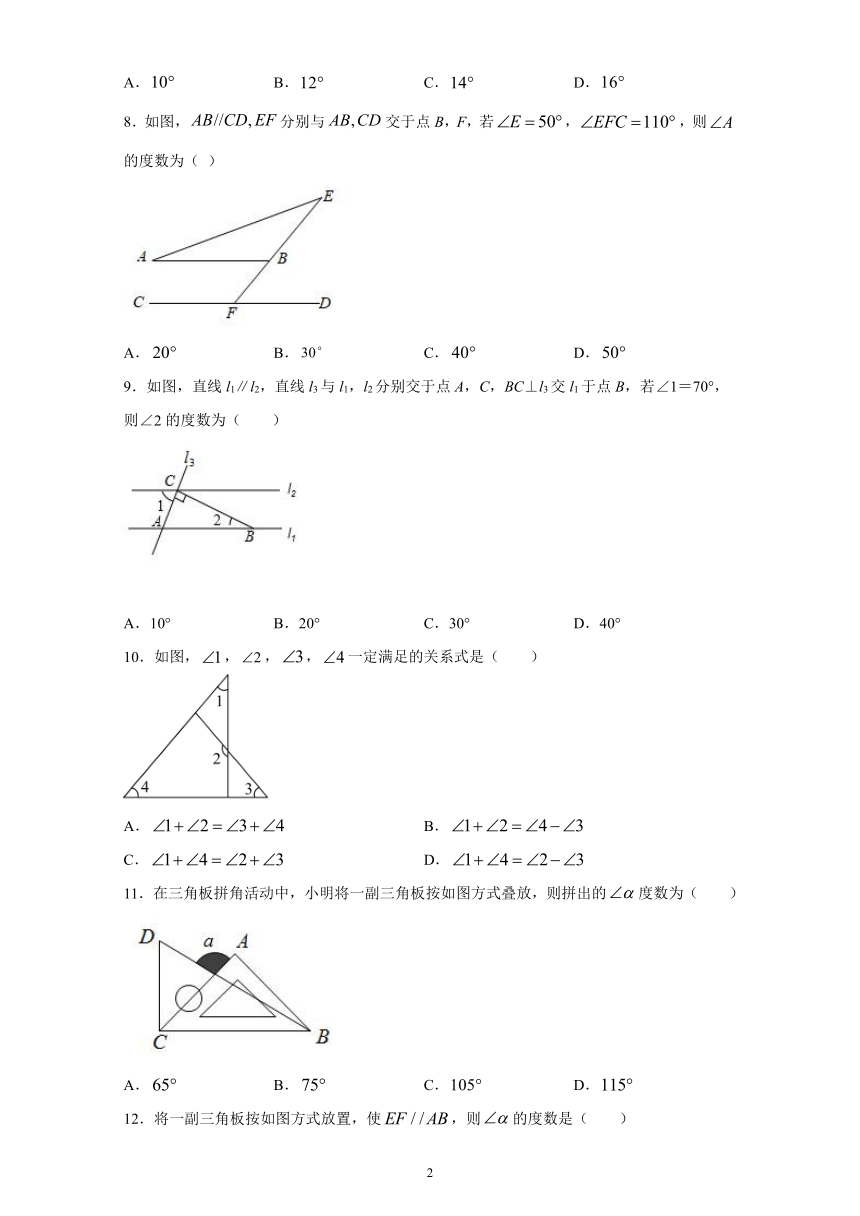
1.如果三角形的三个内角的比是3:4:7,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
2.下面给出的四个三角形都有一部分被遮挡,其中不能判定三角形类型的是(
)
A.
B.
C.
D.
3.如果,那么是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.无法确定
4.下列条件中,能判定为直角三角形的是(
)
A.
B.
C.
D.
5.如图,在中,D为上一点,,,,则的度数为(
)
A.
B.
C.
D.
6.如图,点C是内一点,连,则的度数是(
)
A.
B.
C.
D.
7.如图,是的边上的高,平分,若,,则的度数是(
)
A.
B.
C.
D.
8.如图,分别与交于点B,F,若,,则的度数为(
)
A.
B.
C.
D.
9.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B,若∠1=70°,则∠2的度数为(
)
A.10°
B.20°
C.30°
D.40°
10.如图,,,,一定满足的关系式是(
)
A.
B.
C.
D.
11.在三角板拼角活动中,小明将一副三角板按如图方式叠放,则拼出的度数为(
)
A.
B.
C.
D.
12.将一副三角板按如图方式放置,使,则的度数是(
)
A.
B.
C.
D.
二、填空题
13.如图,,,,_______.
14.如图,将纸片沿折叠,使点落在点处,且平分,平分,若,则______.
15.如图,F为四边形ABCD外一点,连接FB、FC,得到,,若∠A+∠D+∠F=240°,则∠F=_____.
16.当三角形中一个内角是另一个内角的时,我们称此三角形为“希望三角形”,其中称为“希望角”,如果一个“希望三角形”中有一个内角为,那么这个“希望三角形”的“希望角”度数为_______.
17.一副直角三角板按如图所示放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上,点D在AC上,AB与DF相交于点O.若DE∥CF,则∠BOF等于__.
18.如图,把三角形铁皮ABC加工成四边形ABCD形状的零件,∠A=40°,且D恰好是△ABC两条角平分线的交点,工人师傅量得∠BDC=110°,则这个四边形零件加工_____.(填“合格”或“不合格”)
三、解答题
19.如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为70°.
(1)求∠CAF的度数;
(2)求∠AFC的度数.
20.阅读下列材料,并完成相应任务.
三角形的内角和
小学时候我们就知道三角形内角和是180度,学行线之后,可以证明三角形内角和是180度,证明方法如下:
如图1,已知:三角形.求证
证法一:如图2,过点A作直线,∵
∴,
∵
∴,即三角形内角和是
证法二:如图3,延长至M,过点C作…
证法一的思路是用平行线的性质得到,,将三角形内角和问题转化为一个平角,进而得到三角形内角和是,这种方法主要体现的数学思想是转化思想,请运用这一思想将证法二补充完整.
21.(1)已知:如图①的图形我们把它称为“8字形”,试说明:.
(2)如图②,分别平分,若,求的度数.
(3)如图③,直线平分的外角平分的外角,若,则________用的代数式表示)
参考答案
1.B
解:设三个角分别为:3x,4x,7x.
∵3x+4x+7x=180,
∴x=,
∴7x=90°,
所以此三角形为直角三角形.
2.C
解:A、知道两个角,可以计算出第三个角的度数,因此可以判断出三角形类型;
B、露出的角是钝角,因此是钝角三角形;
C、露出的角是锐角,其他两角都不知道,因此不能判断出三角形类型;
D、露出的角是钝角,因此是钝角三角形;
3.C
解:∵∠A+∠B+∠C=180°,
∴∠A+∠C=180°?∠B,
而∠A=∠B?∠C,
∴∠A+∠C=∠B,
∴180°?∠B=∠B,解得∠B=90°,
∴△ABC为直角三角形.
4.D
解:A、∠A+∠B+∠C=180°,而∠A=2∠B=3∠C,则,解得,不能确定△ABC为直角三角形,该选项不符合题意;
B、∠A+∠B+∠C=180°,而∠A+∠B=2∠C,即3∠C=180°,解得∠C=60°,不能确定△ABC为直角三角形,该选项不符合题意;
C、∠A+∠B+∠C=180°,而∠A-∠B=30°,则2∠B+∠C=150°,不能确定△ABC为直角三角形,该选项不符合题意;
D、∠A+∠B+∠C=180°,而,则,解得∠A=
30°
,则∠B=60°,∠C=90°,能确定△ABC为直角三角形,该选项符合题意.
5.C
解:设∠1=∠2=x,
∵∠4=∠3=∠1+∠2=2x,
∴∠DAC=180°-4x,
∵∠BAC=108°,
∴x+180°-4x=108°,
∴x=24°,
∴∠DAC=180°-4×24°=84°.
6.C
解:连接AC并延长,
则∠BCE=∠B+∠BAC,∠DCE=∠D+∠CAD,
∴∠BCD=∠BCE+∠DCE=∠B+∠BAC+∠D+∠CAD=∠B+∠D+∠BAD=130°,
7.A
解:∵平分,,,
∴
又∵是的边上的高,
∴
∴
8.A
解:∵,
∴,
∵,
∴,
∵,
∴;
9.B
解:∵l1∥l2,
∴∠1=∠CAB=70°,
∵BC⊥l3交l1于点B,
∴∠ACB=90°,
∴.
10.D
解:如图,在△BED中,
∠AEF=∠4+∠3,
在△AEF中,
∠2=∠1+∠AEF,
∴∠2=∠1+∠4+∠3,
即∠2–∠3=∠1+∠4,
11.C
解:如图所示:由题意可得,∠ACD=90°﹣45°=45°,
则=∠ACD+∠D=45°+60°=105°.
12.D
解:如图,设BC与EF交于点G.
∵,
∴.
∴.
∵,.
∴.
13.127
解:∵∠BEF是△AEC的一个外角,
∴∠BEF=∠A+∠C=30°+55°=85°,
∵∠DFE是△BEF的一个外角,
∴∠DFE=∠B+∠BEF=42°+85°=127°,
14.
解:连接,
平分,平分,,
,
,
,
,,
,,
,
15.
解:由四边形内角和可得:,
∵,,
∴,
∵,
∴,即,
∵,
∴,即,
∵∠A+∠D+∠F=240°,
∴,即,
∴;
16.36°或72°或96°
解:①36°角是α,则希望角度数为36°;
②36°角是β,则α=β=36°,
所以,希望角α=72°;
③36°角既不是α也不是β,
则α+β+36°=180°,
所以,α+α+36°=180°,
解得α=96°,
综上所述,希望角度数为36°或72°或96°.
17.15°.
解:∵∠C=∠DFE=90°,∠A=45°,∠E=60°,
∴∠EDF=30°,∠ABC=45°,
∵DE∥CF,
∴∠OFB=∠EDF=30°,
∴∠BOF=∠ABC﹣∠OFB=45°﹣30°=15°.
18.合格
解:∵∠A=40°,
∴,
∵BD、CD分别平分∠ABC和∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=∠ABC+∠ACB=×=70°,
∴∠BDC=110°,
∴这个四边形零件加工合格,
19.(1)40°;(2)130°
解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣30°﹣70°=80°,
又∵AE平分∠BAC,
∴∠CAF=∠CAB=×80°=40°;
(2)∵CD为△ABC的高,∠CAD=80°,
∴Rt△ACD中,∠ACF=90°﹣80°=10°,
∴∠AFC=180°﹣∠ACF﹣∠CAF=180°﹣10°﹣40°=130°.
20.见解析
解:证明:∵CN∥AB
∴∠A=∠ACN,∠B=∠NCM,
∵∠ACB+∠ACN+∠NCM=180°,
∴∠ACB+∠BAC+∠ABC=180°.
21.(1)证明见解析;(2);(3).
解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)∵分别平分,
设∠BAP=∠PAD=x,∠BCP=∠PCD=y,
则有,
∴∠ABC-∠P=∠P-∠ADC,
∴;
(3)如图,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°-∠2=180°-∠1,∠PCD=180°-∠3,
∵∠P+(180°-∠1)=∠ADC+(180°-∠3),
∠P+∠1=∠ABC+∠4,
∴2∠P=∠ABC+∠ADC,
∵,
∴.
一、单选题
1.如果三角形的三个内角的比是3:4:7,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
2.下面给出的四个三角形都有一部分被遮挡,其中不能判定三角形类型的是(
)
A.
B.
C.
D.
3.如果,那么是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.无法确定
4.下列条件中,能判定为直角三角形的是(
)
A.
B.
C.
D.
5.如图,在中,D为上一点,,,,则的度数为(
)
A.
B.
C.
D.
6.如图,点C是内一点,连,则的度数是(
)
A.
B.
C.
D.
7.如图,是的边上的高,平分,若,,则的度数是(
)
A.
B.
C.
D.
8.如图,分别与交于点B,F,若,,则的度数为(
)
A.
B.
C.
D.
9.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B,若∠1=70°,则∠2的度数为(
)
A.10°
B.20°
C.30°
D.40°
10.如图,,,,一定满足的关系式是(
)
A.
B.
C.
D.
11.在三角板拼角活动中,小明将一副三角板按如图方式叠放,则拼出的度数为(
)
A.
B.
C.
D.
12.将一副三角板按如图方式放置,使,则的度数是(
)
A.
B.
C.
D.
二、填空题
13.如图,,,,_______.
14.如图,将纸片沿折叠,使点落在点处,且平分,平分,若,则______.
15.如图,F为四边形ABCD外一点,连接FB、FC,得到,,若∠A+∠D+∠F=240°,则∠F=_____.
16.当三角形中一个内角是另一个内角的时,我们称此三角形为“希望三角形”,其中称为“希望角”,如果一个“希望三角形”中有一个内角为,那么这个“希望三角形”的“希望角”度数为_______.
17.一副直角三角板按如图所示放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上,点D在AC上,AB与DF相交于点O.若DE∥CF,则∠BOF等于__.
18.如图,把三角形铁皮ABC加工成四边形ABCD形状的零件,∠A=40°,且D恰好是△ABC两条角平分线的交点,工人师傅量得∠BDC=110°,则这个四边形零件加工_____.(填“合格”或“不合格”)
三、解答题
19.如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为70°.
(1)求∠CAF的度数;
(2)求∠AFC的度数.
20.阅读下列材料,并完成相应任务.
三角形的内角和
小学时候我们就知道三角形内角和是180度,学行线之后,可以证明三角形内角和是180度,证明方法如下:
如图1,已知:三角形.求证
证法一:如图2,过点A作直线,∵
∴,
∵
∴,即三角形内角和是
证法二:如图3,延长至M,过点C作…
证法一的思路是用平行线的性质得到,,将三角形内角和问题转化为一个平角,进而得到三角形内角和是,这种方法主要体现的数学思想是转化思想,请运用这一思想将证法二补充完整.
21.(1)已知:如图①的图形我们把它称为“8字形”,试说明:.
(2)如图②,分别平分,若,求的度数.
(3)如图③,直线平分的外角平分的外角,若,则________用的代数式表示)
参考答案
1.B
解:设三个角分别为:3x,4x,7x.
∵3x+4x+7x=180,
∴x=,
∴7x=90°,
所以此三角形为直角三角形.
2.C
解:A、知道两个角,可以计算出第三个角的度数,因此可以判断出三角形类型;
B、露出的角是钝角,因此是钝角三角形;
C、露出的角是锐角,其他两角都不知道,因此不能判断出三角形类型;
D、露出的角是钝角,因此是钝角三角形;
3.C
解:∵∠A+∠B+∠C=180°,
∴∠A+∠C=180°?∠B,
而∠A=∠B?∠C,
∴∠A+∠C=∠B,
∴180°?∠B=∠B,解得∠B=90°,
∴△ABC为直角三角形.
4.D
解:A、∠A+∠B+∠C=180°,而∠A=2∠B=3∠C,则,解得,不能确定△ABC为直角三角形,该选项不符合题意;
B、∠A+∠B+∠C=180°,而∠A+∠B=2∠C,即3∠C=180°,解得∠C=60°,不能确定△ABC为直角三角形,该选项不符合题意;
C、∠A+∠B+∠C=180°,而∠A-∠B=30°,则2∠B+∠C=150°,不能确定△ABC为直角三角形,该选项不符合题意;
D、∠A+∠B+∠C=180°,而,则,解得∠A=
30°
,则∠B=60°,∠C=90°,能确定△ABC为直角三角形,该选项符合题意.
5.C
解:设∠1=∠2=x,
∵∠4=∠3=∠1+∠2=2x,
∴∠DAC=180°-4x,
∵∠BAC=108°,
∴x+180°-4x=108°,
∴x=24°,
∴∠DAC=180°-4×24°=84°.
6.C
解:连接AC并延长,
则∠BCE=∠B+∠BAC,∠DCE=∠D+∠CAD,
∴∠BCD=∠BCE+∠DCE=∠B+∠BAC+∠D+∠CAD=∠B+∠D+∠BAD=130°,
7.A
解:∵平分,,,
∴
又∵是的边上的高,
∴
∴
8.A
解:∵,
∴,
∵,
∴,
∵,
∴;
9.B
解:∵l1∥l2,
∴∠1=∠CAB=70°,
∵BC⊥l3交l1于点B,
∴∠ACB=90°,
∴.
10.D
解:如图,在△BED中,
∠AEF=∠4+∠3,
在△AEF中,
∠2=∠1+∠AEF,
∴∠2=∠1+∠4+∠3,
即∠2–∠3=∠1+∠4,
11.C
解:如图所示:由题意可得,∠ACD=90°﹣45°=45°,
则=∠ACD+∠D=45°+60°=105°.
12.D
解:如图,设BC与EF交于点G.
∵,
∴.
∴.
∵,.
∴.
13.127
解:∵∠BEF是△AEC的一个外角,
∴∠BEF=∠A+∠C=30°+55°=85°,
∵∠DFE是△BEF的一个外角,
∴∠DFE=∠B+∠BEF=42°+85°=127°,
14.
解:连接,
平分,平分,,
,
,
,
,,
,,
,
15.
解:由四边形内角和可得:,
∵,,
∴,
∵,
∴,即,
∵,
∴,即,
∵∠A+∠D+∠F=240°,
∴,即,
∴;
16.36°或72°或96°
解:①36°角是α,则希望角度数为36°;
②36°角是β,则α=β=36°,
所以,希望角α=72°;
③36°角既不是α也不是β,
则α+β+36°=180°,
所以,α+α+36°=180°,
解得α=96°,
综上所述,希望角度数为36°或72°或96°.
17.15°.
解:∵∠C=∠DFE=90°,∠A=45°,∠E=60°,
∴∠EDF=30°,∠ABC=45°,
∵DE∥CF,
∴∠OFB=∠EDF=30°,
∴∠BOF=∠ABC﹣∠OFB=45°﹣30°=15°.
18.合格
解:∵∠A=40°,
∴,
∵BD、CD分别平分∠ABC和∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=∠ABC+∠ACB=×=70°,
∴∠BDC=110°,
∴这个四边形零件加工合格,
19.(1)40°;(2)130°
解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣30°﹣70°=80°,
又∵AE平分∠BAC,
∴∠CAF=∠CAB=×80°=40°;
(2)∵CD为△ABC的高,∠CAD=80°,
∴Rt△ACD中,∠ACF=90°﹣80°=10°,
∴∠AFC=180°﹣∠ACF﹣∠CAF=180°﹣10°﹣40°=130°.
20.见解析
解:证明:∵CN∥AB
∴∠A=∠ACN,∠B=∠NCM,
∵∠ACB+∠ACN+∠NCM=180°,
∴∠ACB+∠BAC+∠ABC=180°.
21.(1)证明见解析;(2);(3).
解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)∵分别平分,
设∠BAP=∠PAD=x,∠BCP=∠PCD=y,
则有,
∴∠ABC-∠P=∠P-∠ADC,
∴;
(3)如图,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°-∠2=180°-∠1,∠PCD=180°-∠3,
∵∠P+(180°-∠1)=∠ADC+(180°-∠3),
∠P+∠1=∠ABC+∠4,
∴2∠P=∠ABC+∠ADC,
∵,
∴.
