2020-2021学年七年级数学华东师大版下册 9.2多边形的内角和与外角和练习(word解析版)
文档属性
| 名称 | 2020-2021学年七年级数学华东师大版下册 9.2多边形的内角和与外角和练习(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 86.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 00:00:00 | ||
图片预览

文档简介
9.2多边形的内角和与外角和
一.选择题
1.若一个多边形的每个外角都是72°,则该多边形的边数为( )
A.3 B.4 C.5 D.6
2.四边形的内角和与外角和的数量关系,正确的是( )
A.内角和比外角和大180° B.外角和比内角和大180°
C.内角和比外角和大360° D.内角和与外角和相等
3.如果一个多边形的内角和等于它的外角和的3倍,则这个多边形是( )
A.三角形 B.四边形 C.六边形 D.八边形
4.如图,足球图片中的一块黑色皮块的内角和接近于( )
A.720° B.540° C.360° D.180°
5.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
6.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A.90° B.270° C.210° D.180°
7.如果一个n边形的外角和是内角和的一半,则该多边形的边数n的值为( )
A.6 B.7 C.8 D.9
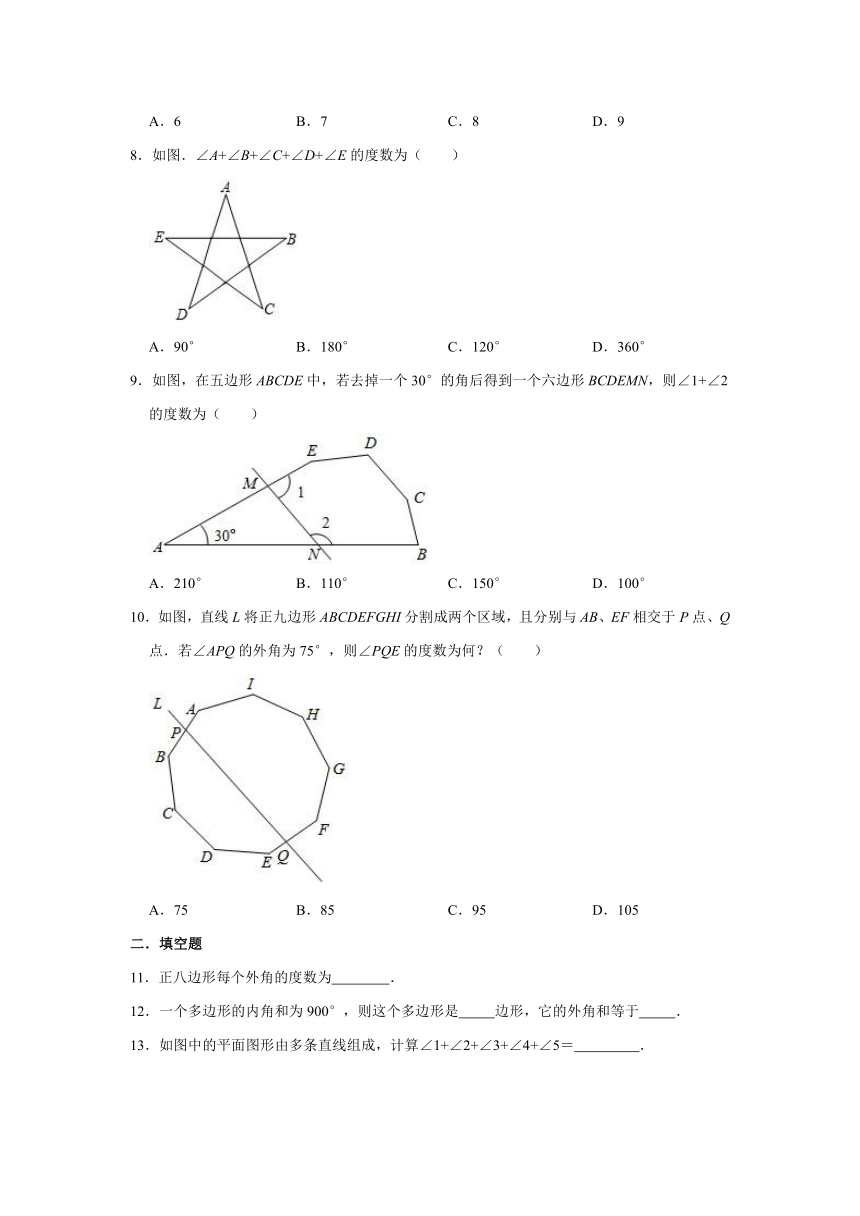
8.如图.∠A+∠B+∠C+∠D+∠E的度数为( )
A.90° B.180° C.120° D.360°
9.如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )
A.210° B.110° C.150° D.100°
10.如图,直线L将正九边形ABCDEFGHI分割成两个区域,且分别与AB、EF相交于P点、Q点.若∠APQ的外角为75°,则∠PQE的度数为何?( )
A.75 B.85 C.95 D.105
二.填空题
11.正八边形每个外角的度数为 .
12.一个多边形的内角和为900°,则这个多边形是 边形,它的外角和等于 .
13.如图中的平面图形由多条直线组成,计算∠1+∠2+∠3+∠4+∠5= .
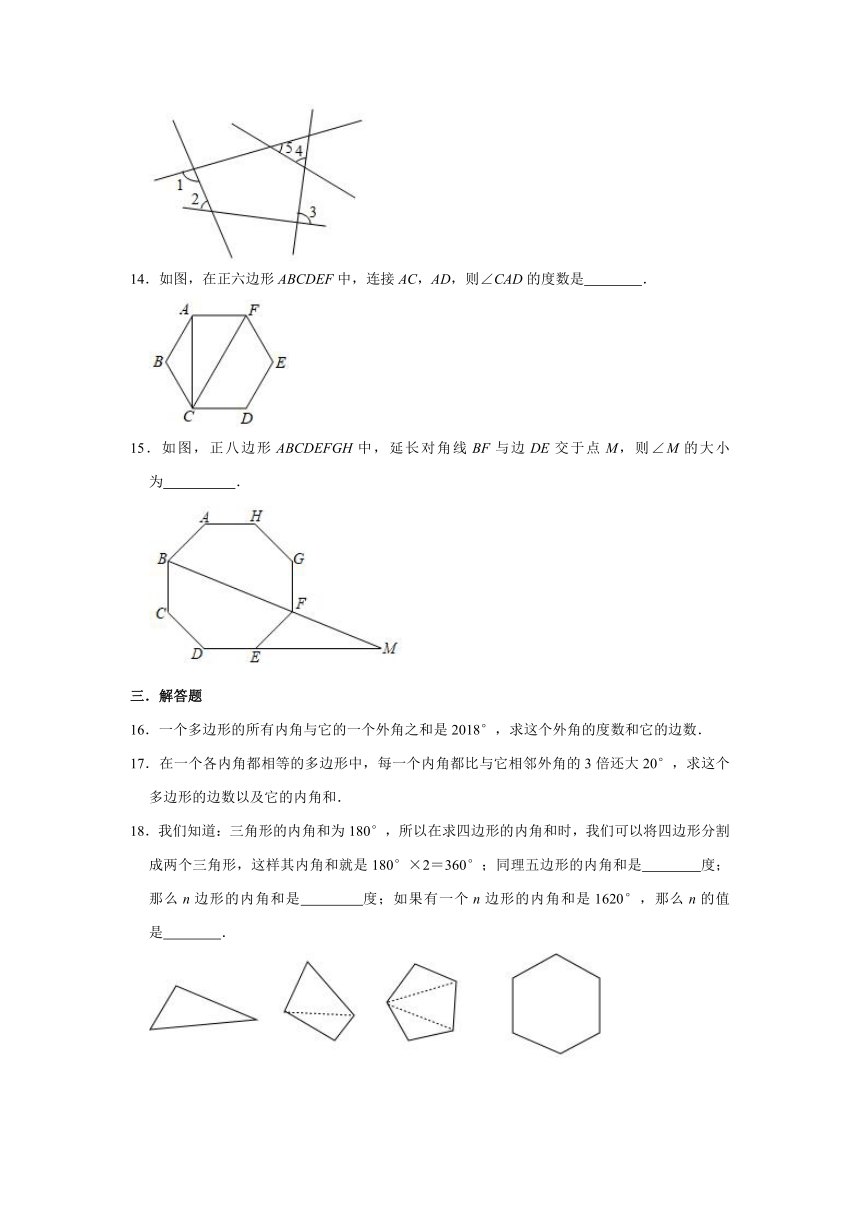
14.如图,在正六边形ABCDEF中,连接AC,AD,则∠CAD的度数是 .
15.如图,正八边形ABCDEFGH中,延长对角线BF与边DE交于点M,则∠M的大小为 .
三.解答题
16.一个多边形的所有内角与它的一个外角之和是2018°,求这个外角的度数和它的边数.
17.在一个各内角都相等的多边形中,每一个内角都比与它相邻外角的3倍还大20°,求这个多边形的边数以及它的内角和.
18.我们知道:三角形的内角和为180°,所以在求四边形的内角和时,我们可以将四边形分割成两个三角形,这样其内角和就是180°×2=360°;同理五边形的内角和是 度;那么n边形的内角和是 度;如果有一个n边形的内角和是1620°,那么n的值是 .
参考答案
一.选择题
1.解:360°÷72°=5.
故这个多边形是五边形.
故选:C.
2.解:A.四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
B.四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
C.六四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
D.四边形的内角和与外角和相等,都等于360°,故本选项表述正确.
故选:D.
3.解:设多边形的边数为n,依题意,得
(n﹣2)?180°=3×360°,
解得n=8,
故选:D.
4.解:因为黑色皮块是正五边形,
所以黑色皮块的内角和是(5﹣2)×180°=540°.
故选:B.
5.解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
6.解:延长AB,DC,
∵AB∥CD,
∴∠4+∠5=180°,
根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故选:D.
7.解:由题意得(n﹣2)?180°×=360°,
解得n=6.
故选:A.
8.解:如图:
∵∠1=∠2+∠C,∠2=∠A+∠D,
∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
故选:B.
9.解:解法一:
∵∠A+∠B+∠C+∠D+∠E=(5﹣2)×180°=540°,∠A=30°,
∴∠B+∠C+∠D+∠E=510°,
∵∠1+∠2+∠B+∠C+∠D+∠E=(6﹣2)×180°=720°,
∴∠1+∠2=720°﹣510°=210°,
解法二:在△ANM中,∠ANM+∠AMN=180°﹣∠A=180°﹣30°=150°,
∴∠1+∠2=360°﹣(∠AMN+∠ANM)=360°﹣150°=210°
故选:A.
10.解:∵∠APQ的外角为75°,
∴∠BPQ=75°,
∵正九边形的内角和=(9﹣2)×180°=1260°,
∴∠B=∠C=∠D=∠E=1260°÷9=140°,
∵六边形PBCDEQ的内角和=(6﹣2)×180°=∠B+∠C+∠D+∠E+∠BPQ+∠PQE,
∴720°=75°+140°×4+∠PQE,
∴∠PQE=85°,
故选:B.
二.填空题
11.解:因为任何一个多边形的外角和都是360°,
所以正八边形的每个外角的度数是:360°÷8=45.
故答案为:45°.
12.解:设这个多边形是n边形,
根据题意得:(n﹣2)?180°=900°,
解得n=7.
它的外角和等于360°.
故答案为:七,360°.
13.解:由图可知,∠1+∠2+∠3+∠4+∠5=360°.
故答案为:360°.
14.解:如图,
正六边形的每个内角为:=120°,
∴∠BAC==30°,
∵六边形是轴对称图形,
∴∠BAD==60°,
∴∠CAD=∠BAD﹣∠BAC=30°.
故答案为:30°.
15.解:∵八边形ABCDEFGH是正八边形,
∴∠DEF=(8﹣2)×180°÷8=135°,
∴∠FEM=45°
∴∠DEF=∠EFG
∵BF平分∠EFG
∴∠EFB=∠BFE==67.5°,
∵∠BFE=∠FEM+∠M,
∴∠M=∠BFE﹣∠FEM
∴∠M=22.5°.
故答案为:22.5°.
三.解答题
16.解:设这个多边形的边数是n,n为正整数,
根据题意得:0°<2018°﹣(n﹣2)×180°<180°,
解得:<n<,
即n=13,
这个外角为2018°﹣(13﹣2)×180°=38°.
17.解:设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20°)+α=180°,解得α=40°,
即多边形的每个外角为40°,
又∵多边形的外角和为360°,
∴多边形的外角个数==9,
∴多边形的边数=9,
∴多边形的内角和=(9﹣2)×180°=1260°.
18.解:180°×(5﹣2)=540°;
180°(n﹣2)=(180n﹣360)°;
∵(n﹣2)×180°=1620°,
∴n﹣2=9,
∴n=11,
故答案为:540;(180n﹣360);11.
一.选择题
1.若一个多边形的每个外角都是72°,则该多边形的边数为( )
A.3 B.4 C.5 D.6
2.四边形的内角和与外角和的数量关系,正确的是( )
A.内角和比外角和大180° B.外角和比内角和大180°
C.内角和比外角和大360° D.内角和与外角和相等
3.如果一个多边形的内角和等于它的外角和的3倍,则这个多边形是( )
A.三角形 B.四边形 C.六边形 D.八边形
4.如图,足球图片中的一块黑色皮块的内角和接近于( )
A.720° B.540° C.360° D.180°
5.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
6.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A.90° B.270° C.210° D.180°
7.如果一个n边形的外角和是内角和的一半,则该多边形的边数n的值为( )
A.6 B.7 C.8 D.9
8.如图.∠A+∠B+∠C+∠D+∠E的度数为( )
A.90° B.180° C.120° D.360°
9.如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )
A.210° B.110° C.150° D.100°
10.如图,直线L将正九边形ABCDEFGHI分割成两个区域,且分别与AB、EF相交于P点、Q点.若∠APQ的外角为75°,则∠PQE的度数为何?( )
A.75 B.85 C.95 D.105
二.填空题
11.正八边形每个外角的度数为 .
12.一个多边形的内角和为900°,则这个多边形是 边形,它的外角和等于 .
13.如图中的平面图形由多条直线组成,计算∠1+∠2+∠3+∠4+∠5= .
14.如图,在正六边形ABCDEF中,连接AC,AD,则∠CAD的度数是 .
15.如图,正八边形ABCDEFGH中,延长对角线BF与边DE交于点M,则∠M的大小为 .
三.解答题
16.一个多边形的所有内角与它的一个外角之和是2018°,求这个外角的度数和它的边数.
17.在一个各内角都相等的多边形中,每一个内角都比与它相邻外角的3倍还大20°,求这个多边形的边数以及它的内角和.
18.我们知道:三角形的内角和为180°,所以在求四边形的内角和时,我们可以将四边形分割成两个三角形,这样其内角和就是180°×2=360°;同理五边形的内角和是 度;那么n边形的内角和是 度;如果有一个n边形的内角和是1620°,那么n的值是 .
参考答案
一.选择题
1.解:360°÷72°=5.
故这个多边形是五边形.
故选:C.
2.解:A.四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
B.四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
C.六四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
D.四边形的内角和与外角和相等,都等于360°,故本选项表述正确.
故选:D.
3.解:设多边形的边数为n,依题意,得
(n﹣2)?180°=3×360°,
解得n=8,
故选:D.
4.解:因为黑色皮块是正五边形,
所以黑色皮块的内角和是(5﹣2)×180°=540°.
故选:B.
5.解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
6.解:延长AB,DC,
∵AB∥CD,
∴∠4+∠5=180°,
根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故选:D.
7.解:由题意得(n﹣2)?180°×=360°,
解得n=6.
故选:A.
8.解:如图:
∵∠1=∠2+∠C,∠2=∠A+∠D,
∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
故选:B.
9.解:解法一:
∵∠A+∠B+∠C+∠D+∠E=(5﹣2)×180°=540°,∠A=30°,
∴∠B+∠C+∠D+∠E=510°,
∵∠1+∠2+∠B+∠C+∠D+∠E=(6﹣2)×180°=720°,
∴∠1+∠2=720°﹣510°=210°,
解法二:在△ANM中,∠ANM+∠AMN=180°﹣∠A=180°﹣30°=150°,
∴∠1+∠2=360°﹣(∠AMN+∠ANM)=360°﹣150°=210°
故选:A.
10.解:∵∠APQ的外角为75°,
∴∠BPQ=75°,
∵正九边形的内角和=(9﹣2)×180°=1260°,
∴∠B=∠C=∠D=∠E=1260°÷9=140°,
∵六边形PBCDEQ的内角和=(6﹣2)×180°=∠B+∠C+∠D+∠E+∠BPQ+∠PQE,
∴720°=75°+140°×4+∠PQE,
∴∠PQE=85°,
故选:B.
二.填空题
11.解:因为任何一个多边形的外角和都是360°,
所以正八边形的每个外角的度数是:360°÷8=45.
故答案为:45°.
12.解:设这个多边形是n边形,
根据题意得:(n﹣2)?180°=900°,
解得n=7.
它的外角和等于360°.
故答案为:七,360°.
13.解:由图可知,∠1+∠2+∠3+∠4+∠5=360°.
故答案为:360°.
14.解:如图,
正六边形的每个内角为:=120°,
∴∠BAC==30°,
∵六边形是轴对称图形,
∴∠BAD==60°,
∴∠CAD=∠BAD﹣∠BAC=30°.
故答案为:30°.
15.解:∵八边形ABCDEFGH是正八边形,
∴∠DEF=(8﹣2)×180°÷8=135°,
∴∠FEM=45°
∴∠DEF=∠EFG
∵BF平分∠EFG
∴∠EFB=∠BFE==67.5°,
∵∠BFE=∠FEM+∠M,
∴∠M=∠BFE﹣∠FEM
∴∠M=22.5°.
故答案为:22.5°.
三.解答题
16.解:设这个多边形的边数是n,n为正整数,
根据题意得:0°<2018°﹣(n﹣2)×180°<180°,
解得:<n<,
即n=13,
这个外角为2018°﹣(13﹣2)×180°=38°.
17.解:设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20°)+α=180°,解得α=40°,
即多边形的每个外角为40°,
又∵多边形的外角和为360°,
∴多边形的外角个数==9,
∴多边形的边数=9,
∴多边形的内角和=(9﹣2)×180°=1260°.
18.解:180°×(5﹣2)=540°;
180°(n﹣2)=(180n﹣360)°;
∵(n﹣2)×180°=1620°,
∴n﹣2=9,
∴n=11,
故答案为:540;(180n﹣360);11.
