2020—2021学年华东师大版数学七年级下册10.1.1生活中的轴对称课件(32张ppt)
文档属性
| 名称 | 2020—2021学年华东师大版数学七年级下册10.1.1生活中的轴对称课件(32张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 08:41:57 | ||
图片预览











文档简介
10.1.1生活中的轴对称
能用自己的话描述轴对称图形和两个图形成轴对称的概念.
能总结出轴对称图形及两个图形成轴对称的区别与联系.
学习目标
1
2
3
能分辨轴对称图形并找出它的对称轴.
找出轴对称图形的对称轴.
学习重难点
总结出轴对称图形及两个图形成轴对称的区别与联系。
重点:
难点:
创设情境
创设情境
创设情境
创设情境
创设情境
创设情境
不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.山倒映在湖中,这是令人难忘的对称景象.自远古以来,对称的形式都被认为是和谐美丽的.
导入新课
讲授新课
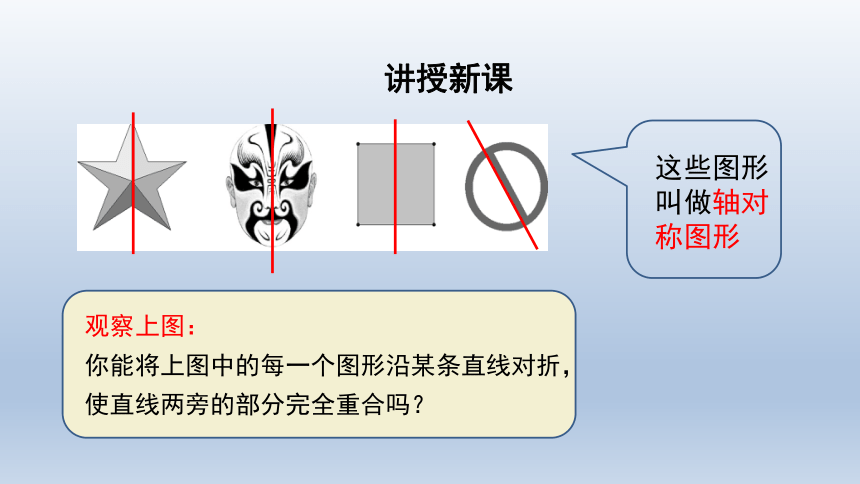
观察上图:
你能将上图中的每一个图形沿某条直线对折,使直线两旁的部分完全重合吗?
这些图形叫做轴对称图形
一个图形沿某条直线对折,对折的两部分能完全重合的,那么就称这样的图形为轴对称图形.
这条直线即为这个图形的对称轴.
轴对称图形:
总结概念
1.概念满足两个条件:①一个图形;②沿一条直线对折,直线两旁的部分能够互相重合,二者缺一不可.
2.轴对称图形是一个图形.
3.对称轴是一条直线.
概念解读
总结概念
探究演练
画出下列六角星的对称轴:
(5条对称轴)
(1条对称轴)
(4条对称轴)
(2条对称轴)
归纳: 轴对称图形的对称轴不一定只有一条.
探究演练
将一张矩形纸对折,然后用笔尖扎出“17”这个数字,将纸打开后铺平,
探究演练
⑴图中的两个“17”有什么特点?
⑵在扎出的字中找出两组对应点,并连接,你连接段与对称轴有什么关系?
⑶在扎出的字中找出两组对应线段,对应线段是什么关系?
探究演练
答:(1)图中的两个“17”是关于折痕对称的;
(2)垂直;
(3)平行。
探究演练
下列两组图形,将它们沿着虚线对折后有什么特点?
A
B
C
第一组
第二组
左右两边的两个图形完全重合
称为两个图形成轴对称
观 察
两个图形成轴对称:
把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
概念总结
1.概念满足两个条件:①两个图形;②沿一条直线对折,两个图形能够互相重合,二者缺一不可.
2.两个图形成轴对称是指两个图形.
总结概念
概念解读
请你标出下图中 A、B、C 三点的对称点A1、B1、C1.
过点A作对称轴的垂线,垂足为O1,延长AO1到A1,使AO1=A1O1.,即A1为 所求对称点;同理,可作出点B1、C1 。
O1
A1
AO1=A1O1
做一做
易知,A点与____点重合,B点与____点重合,C点与_____重合.
所以,∠A=_____, ∠B=_____, ∠C=_____,BC=______.
总结概括
A1
B1
C1
A1
B1
C1
∠A1
∠B1
∠C1
B1C1
在纸的一侧上滴几滴墨水,将纸迅速对折、压平,并用手指压出清晰的折痕,再将纸打开后铺平,观察所得到的图案,位于折痕两侧墨水图案彼此之间有什么关系?它的对称轴是什么呢?
位于折痕两侧墨水图案成轴对称 ,对称轴为折痕所在直线.
做一做
轴对称图形(或两个图形成轴对称)的基本特征:
轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等。
总结概括
1.观察下列各种图形,判断是不是轴对称图形?并画出该轴对称图形的对称轴?
课堂练习
课堂练习
课堂小结
轴对称图形:
如果沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形;这条直线叫做这个图形的轴。
课堂小结
轴对称:
把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
轴对称图形和轴对称的区别与联系?
区别:
(1)、轴对称是两个图形之间的对称关系,轴对称图形是一个图 形自身的对称特征.
(2)、轴对称的对称点,分别在两个图形上;轴对称图形的对称点都在同一个图形上.
(3)、轴对称有一条对称轴;轴对称图形至少有一条对称轴.
课堂小结
(2)、它们可以互相转化;如果把轴对称的两个图形看作一个整体,那么它就是一个轴对称图形;如果把轴对称图形沿对称轴分成两个部分,那么两个部分就是关于这条对称轴成轴对称。
课堂小结
联系:(1)、都沿某直线翻折后能够互相重合。
谢谢听讲!
能用自己的话描述轴对称图形和两个图形成轴对称的概念.
能总结出轴对称图形及两个图形成轴对称的区别与联系.
学习目标
1
2
3
能分辨轴对称图形并找出它的对称轴.
找出轴对称图形的对称轴.
学习重难点
总结出轴对称图形及两个图形成轴对称的区别与联系。
重点:
难点:
创设情境
创设情境
创设情境
创设情境
创设情境
创设情境
不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.山倒映在湖中,这是令人难忘的对称景象.自远古以来,对称的形式都被认为是和谐美丽的.
导入新课
讲授新课
观察上图:
你能将上图中的每一个图形沿某条直线对折,使直线两旁的部分完全重合吗?
这些图形叫做轴对称图形
一个图形沿某条直线对折,对折的两部分能完全重合的,那么就称这样的图形为轴对称图形.
这条直线即为这个图形的对称轴.
轴对称图形:
总结概念
1.概念满足两个条件:①一个图形;②沿一条直线对折,直线两旁的部分能够互相重合,二者缺一不可.
2.轴对称图形是一个图形.
3.对称轴是一条直线.
概念解读
总结概念
探究演练
画出下列六角星的对称轴:
(5条对称轴)
(1条对称轴)
(4条对称轴)
(2条对称轴)
归纳: 轴对称图形的对称轴不一定只有一条.
探究演练
将一张矩形纸对折,然后用笔尖扎出“17”这个数字,将纸打开后铺平,
探究演练
⑴图中的两个“17”有什么特点?
⑵在扎出的字中找出两组对应点,并连接,你连接段与对称轴有什么关系?
⑶在扎出的字中找出两组对应线段,对应线段是什么关系?
探究演练
答:(1)图中的两个“17”是关于折痕对称的;
(2)垂直;
(3)平行。
探究演练
下列两组图形,将它们沿着虚线对折后有什么特点?
A
B
C
第一组
第二组
左右两边的两个图形完全重合
称为两个图形成轴对称
观 察
两个图形成轴对称:
把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
概念总结
1.概念满足两个条件:①两个图形;②沿一条直线对折,两个图形能够互相重合,二者缺一不可.
2.两个图形成轴对称是指两个图形.
总结概念
概念解读
请你标出下图中 A、B、C 三点的对称点A1、B1、C1.
过点A作对称轴的垂线,垂足为O1,延长AO1到A1,使AO1=A1O1.,即A1为 所求对称点;同理,可作出点B1、C1 。
O1
A1
AO1=A1O1
做一做
易知,A点与____点重合,B点与____点重合,C点与_____重合.
所以,∠A=_____, ∠B=_____, ∠C=_____,BC=______.
总结概括
A1
B1
C1
A1
B1
C1
∠A1
∠B1
∠C1
B1C1
在纸的一侧上滴几滴墨水,将纸迅速对折、压平,并用手指压出清晰的折痕,再将纸打开后铺平,观察所得到的图案,位于折痕两侧墨水图案彼此之间有什么关系?它的对称轴是什么呢?
位于折痕两侧墨水图案成轴对称 ,对称轴为折痕所在直线.
做一做
轴对称图形(或两个图形成轴对称)的基本特征:
轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等。
总结概括
1.观察下列各种图形,判断是不是轴对称图形?并画出该轴对称图形的对称轴?
课堂练习
课堂练习
课堂小结
轴对称图形:
如果沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形;这条直线叫做这个图形的轴。
课堂小结
轴对称:
把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
轴对称图形和轴对称的区别与联系?
区别:
(1)、轴对称是两个图形之间的对称关系,轴对称图形是一个图 形自身的对称特征.
(2)、轴对称的对称点,分别在两个图形上;轴对称图形的对称点都在同一个图形上.
(3)、轴对称有一条对称轴;轴对称图形至少有一条对称轴.
课堂小结
(2)、它们可以互相转化;如果把轴对称的两个图形看作一个整体,那么它就是一个轴对称图形;如果把轴对称图形沿对称轴分成两个部分,那么两个部分就是关于这条对称轴成轴对称。
课堂小结
联系:(1)、都沿某直线翻折后能够互相重合。
谢谢听讲!
