云南省云大附中2012届高三考前60天理科数学辅导:第1篇 知识、方法 2 函数与导数
文档属性
| 名称 | 云南省云大附中2012届高三考前60天理科数学辅导:第1篇 知识、方法 2 函数与导数 |  | |
| 格式 | zip | ||
| 文件大小 | 272.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-09 18:26:54 | ||
图片预览



文档简介
云南省云大附中2012届高三考前60天理科数学辅导:
第1篇 知识、方法 2 函数与导数
二、函数与导数
1.你对幂的运算,对数运算的法则熟练掌握了吗?的值的大小会判断么?
,,,,,,,,,。
如:的值为________(答:)
如:.已知,则= .
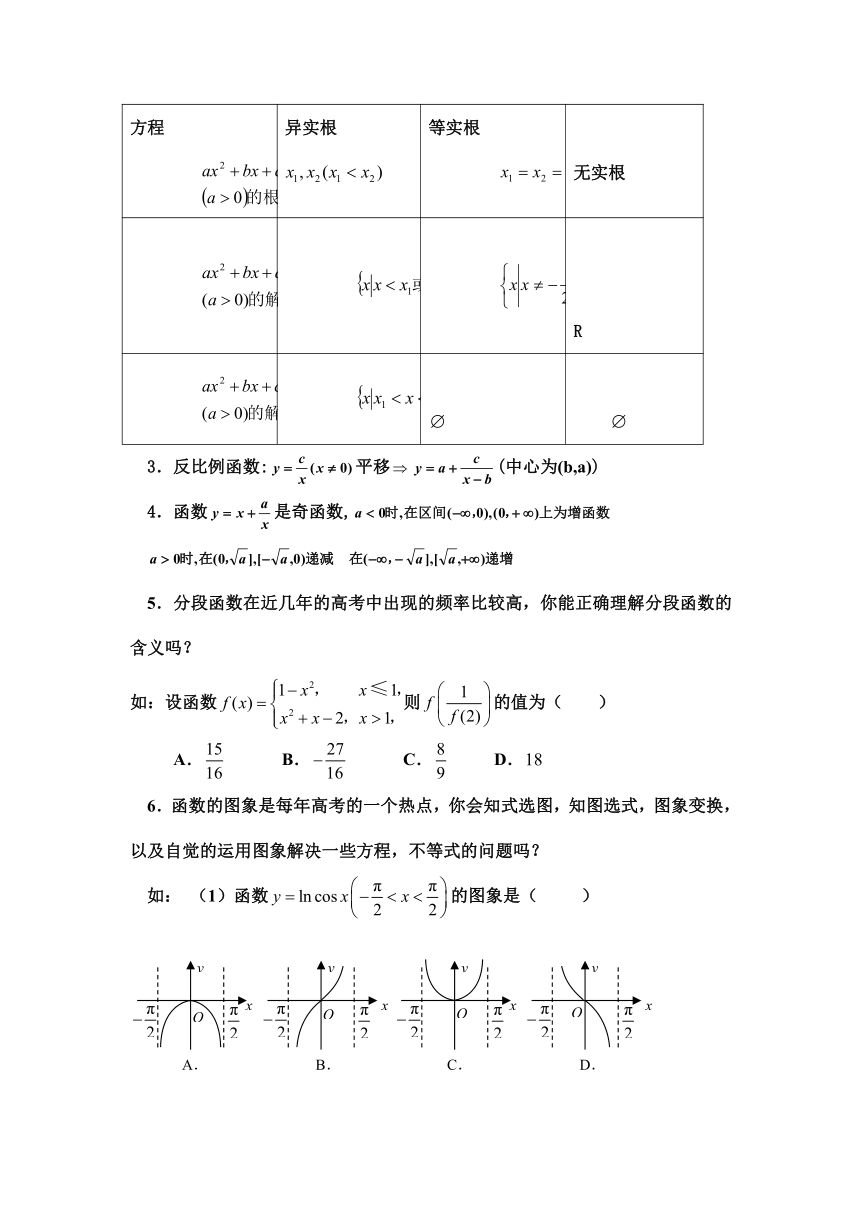
2.二次函数问题①三种形式:一般式f(x)=ax2+bx+c(轴-b/2a,a≠0,顶点 );顶点式f(x)=a(x-h)2+k;零点式f(x)=a(x-x1)(x-x2)(轴 );b=0偶函数;
②三个二次问题熟悉了么?
二次函数()的图象
一元二次方程 有两相异实根 有两相等实根 无实根
R
3.反比例函数:平移(中心为(b,a))
4.函数是奇函数,
5.分段函数在近几年的高考中出现的频率比较高,你能正确理解分段函数的含义吗?
如:设函数则的值为( )
A. B. C. D.
6.函数的图象是每年高考的一个热点,你会知式选图,知图选式,图象变换,以及自觉的运用图象解决一些方程,不等式的问题吗?
如: (1)函数的图象是( )
(2)函数在定义域内可导,其
图象如图,记的导函数为,
则不等式的解集为___________
7.函数的单调性会判断吗①定义法; ⑴单调性的定义:在区间上是增(减)函数当时;
②导数法. 如:已知函数在区间上是增函数,则的取值范围是____(答:));
注意①:能推出为增函数,但反之不一定。如函数在上单调递增,但,∴是为增函数的充分不必要条件。注意②:函数单调性与奇偶性的逆用了吗 .如:已知奇函数是定义在上的减函数,若,求实数的取值范围。(答:)
8.奇偶性:f(x)是偶函数f(-x)=f(x)=f(|x|);f(x)是奇函数f(-x)=-f(x);定义域含零的奇函数过原点(f(0)=0);定义域关于原点对称是为奇函数或偶函数的必要而不充分的条件。
如:(1) 设f(x)是定义在R上的偶函数,,又当时,,则的值为( )
(2)设是连续的偶函数,且当x>0时是单调函数,则满足的所有x之和为( )
A. B. C. D.
(3)设奇函数在上为增函数,且,则不等式的解集为
A. B.
C. D.
9.函数的周期性的判断掌握了吗。
①若函数满足,则的周期为2;②若恒成立,则;③若恒成立,则. ()
如(1)定义在上的偶函数满足,且在上是减函数,若是锐角三角形的两个内角,则的大小关系为_________(答:);
(2)已知定义在上的函数是以2为周期的奇函数,则方程在上至少有__________个实数根(答:5)
10.常见的图象变换掌握了吗?
如(1)要得到的图像,只需作关于_____轴对称的图像,再向____平移3个单位而得到(答:;右);
(2)将函数的图象向右平移2个单位后又向下平移2个单位,所得图象如果与原图象关于直线对称,那么
(答:C)
(3)将函数的图像上所有点的横坐标变为原来的(纵坐标不变),再将此图像沿轴方向向左平移2个单位,所得图像对应的函数为_____(答:);
11.函数的对称性掌握了吗?。
(1)函数关于轴的对称曲线方程为;
(2)函数关于轴的对称曲线方程为;
(3)函数关于原点的对称曲线方程为;
(4)曲线关于直线的对称曲线的方程为
。曲线关于直线的对称曲线的方程为;曲线关于直线的对称曲线的方程为。如:己知函数,若的图像是,它关于直线对称图像是关于原点对称的图像为对应的函数解析式是___________(答:);
(5)曲线关于点的对称曲线的方程为。如若函数与的图象关于点(-2,3)对称,则=______(答:)
①如果函数对于一切,都有,或那么函数的图象关于直线对称是偶函数;
② 如果函数对于一切,都有,那么函数的图象关于点()对称.
③y=f(x)满足f(x +a)=f(x-a)或f(x±2a)=f(x)恒成立,2a为周期;
12.你能画指数函数和对数函数的图象吗 理解指数函数,对数函数的图象通过的特殊点吗?
如:(1) 已知实数满足等式,下列五个关系式:①②③④⑤其中可能成立的关系式有( )
A.①②③ B.①②⑤ C.①③⑤ D.③④⑤
(2)设均为正数,且,,.则( )
A. B. C. D.
13.你对函数的最大值或最小值的概念正确理解了吗
如:(1)设函数的定义域为,有下列三个命题:
①若存在常数,使得对任意有则是函数的最大值;
②若存在使得对任意有则是函数的最大值;
③若存在使得对任意有则是函数的最大值.
这些命题中,真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
(2)已知函数若对恒成立,则的值为
A. B. C . D.
14.什么是函数的零点 函数零点有什么性质 你能正确运用函数零点的性质解决有关方程的根的分布问题吗
练习 函数的零点所在的大致区间是( )
A. B. C. D.
15.你理解导数的几何意义吗 会求经过一点的曲线的切线方程吗 过某点的切线不一定只有一条
如:已知函数(1)求曲线在点处的切线方程;
(2)若过点可作曲线的三条切线,求实数的取值范围.
16.你理解函数的单调性和导数的关系吗 在应用导数研究函数的单调性时,往往需要解含有参数的二次不等式,在进行讨论时,你考虑的全面吗,注意到特殊情况了吗 你是否注意二次项系数为零的情况
如;已知函数,.(Ⅰ)讨论函数的单调区间;
(Ⅱ)设函数在区间内是减函数,求的取值范围.
17。对于形如的复合函数导数的求法,你掌握了吗 这是正确应用导数解决问题的前提.
如:若上是减函数,则的取值范围是( )
A. B. C. D.
18.你理解函数在某点取得极值的必要条件和充分条件吗 函数的导函数,则是为函数极值的必要不充分条件. 给出函数极大(小)值的条件,一定要既考虑,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记。如:设函数,其中.证明:当时,函数没有极值点;当时,函数有且只有一个极值点,并求出极值.
19..在应用导数求参数的范围时,你注意到端点的取舍吗 讨论时遗漏特殊情况了吗
设函数为实数。
(1)已知函数在处取得极值,求的值;
(2)已知不等式对任意都成立,求实数的取值范围。
20.你理解存在性问题和恒成立问题的区别与联系吗 在解题时切不可把二者混为一谈.
遇到含参不等式恒成立求参变量的范围问题,通常采用分离参数法,转化为求某函数的最大值(或最小值);具体地:g(a)>f(x)在x∈A上恒成立 g(a)>f(x)max,g(a)0在x∈A上恒成立f(a,x)min>0, (x∈A)及f(a,x)<0在x∈A上恒成立f(a,x)max>0, (x∈A)来转化;还可以借助于函数图象解决问题。特别关注:“不等式f(a,x)≥0对所有x∈M恒成立”与 “不等式f(a,x)≥0对所有a∈M恒成立”是两个不同的问题,前者是关于x的不等式,而后者则应视为是关于a的不等式。特别提醒:“判别式”只能用于“二次函数对一切实数恒成立”的问题,其它场合,概不适用。
a≥f(x)恒成立a≥[f(x)]max,;a≤f(x)恒成立a≤[f(x)]min;
如:函数. (1).若关于的不等式有解,则实数的取值范围是 ;(2) 若关于的不等式恒成立,则实数的取值范围是 .
21.几类常见的抽象函数 :
①正比例函数型: ---------------;
②幂函数型: --------------,;
③指数函数型: ----------,;
④对数函数型: ---,;
⑤三角函数型: ----- 。
如:(1)已知是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则__(答:0)
(2)已知是定义在上的奇函数,当时,
的图像如右图所示,那么不等式的解集
是_____________(答:);
精品资源,欢迎下载!!
21世纪教育网~~~K@s%U~~~
21世纪教育网
21世纪教育网
21世纪教育网
y
x
O
y
x
O
y
x
O
y
x
O
A.
B.
C.
D.
O 1 2 3 x
y
第1篇 知识、方法 2 函数与导数
二、函数与导数
1.你对幂的运算,对数运算的法则熟练掌握了吗?的值的大小会判断么?
,,,,,,,,,。
如:的值为________(答:)
如:.已知,则= .
2.二次函数问题①三种形式:一般式f(x)=ax2+bx+c(轴-b/2a,a≠0,顶点 );顶点式f(x)=a(x-h)2+k;零点式f(x)=a(x-x1)(x-x2)(轴 );b=0偶函数;
②三个二次问题熟悉了么?
二次函数()的图象
一元二次方程 有两相异实根 有两相等实根 无实根
R
3.反比例函数:平移(中心为(b,a))
4.函数是奇函数,
5.分段函数在近几年的高考中出现的频率比较高,你能正确理解分段函数的含义吗?
如:设函数则的值为( )
A. B. C. D.
6.函数的图象是每年高考的一个热点,你会知式选图,知图选式,图象变换,以及自觉的运用图象解决一些方程,不等式的问题吗?
如: (1)函数的图象是( )
(2)函数在定义域内可导,其
图象如图,记的导函数为,
则不等式的解集为___________
7.函数的单调性会判断吗①定义法; ⑴单调性的定义:在区间上是增(减)函数当时;
②导数法. 如:已知函数在区间上是增函数,则的取值范围是____(答:));
注意①:能推出为增函数,但反之不一定。如函数在上单调递增,但,∴是为增函数的充分不必要条件。注意②:函数单调性与奇偶性的逆用了吗 .如:已知奇函数是定义在上的减函数,若,求实数的取值范围。(答:)
8.奇偶性:f(x)是偶函数f(-x)=f(x)=f(|x|);f(x)是奇函数f(-x)=-f(x);定义域含零的奇函数过原点(f(0)=0);定义域关于原点对称是为奇函数或偶函数的必要而不充分的条件。
如:(1) 设f(x)是定义在R上的偶函数,,又当时,,则的值为( )
(2)设是连续的偶函数,且当x>0时是单调函数,则满足的所有x之和为( )
A. B. C. D.
(3)设奇函数在上为增函数,且,则不等式的解集为
A. B.
C. D.
9.函数的周期性的判断掌握了吗。
①若函数满足,则的周期为2;②若恒成立,则;③若恒成立,则. ()
如(1)定义在上的偶函数满足,且在上是减函数,若是锐角三角形的两个内角,则的大小关系为_________(答:);
(2)已知定义在上的函数是以2为周期的奇函数,则方程在上至少有__________个实数根(答:5)
10.常见的图象变换掌握了吗?
如(1)要得到的图像,只需作关于_____轴对称的图像,再向____平移3个单位而得到(答:;右);
(2)将函数的图象向右平移2个单位后又向下平移2个单位,所得图象如果与原图象关于直线对称,那么
(答:C)
(3)将函数的图像上所有点的横坐标变为原来的(纵坐标不变),再将此图像沿轴方向向左平移2个单位,所得图像对应的函数为_____(答:);
11.函数的对称性掌握了吗?。
(1)函数关于轴的对称曲线方程为;
(2)函数关于轴的对称曲线方程为;
(3)函数关于原点的对称曲线方程为;
(4)曲线关于直线的对称曲线的方程为
。曲线关于直线的对称曲线的方程为;曲线关于直线的对称曲线的方程为。如:己知函数,若的图像是,它关于直线对称图像是关于原点对称的图像为对应的函数解析式是___________(答:);
(5)曲线关于点的对称曲线的方程为。如若函数与的图象关于点(-2,3)对称,则=______(答:)
①如果函数对于一切,都有,或那么函数的图象关于直线对称是偶函数;
② 如果函数对于一切,都有,那么函数的图象关于点()对称.
③y=f(x)满足f(x +a)=f(x-a)或f(x±2a)=f(x)恒成立,2a为周期;
12.你能画指数函数和对数函数的图象吗 理解指数函数,对数函数的图象通过的特殊点吗?
如:(1) 已知实数满足等式,下列五个关系式:①②③④⑤其中可能成立的关系式有( )
A.①②③ B.①②⑤ C.①③⑤ D.③④⑤
(2)设均为正数,且,,.则( )
A. B. C. D.
13.你对函数的最大值或最小值的概念正确理解了吗
如:(1)设函数的定义域为,有下列三个命题:
①若存在常数,使得对任意有则是函数的最大值;
②若存在使得对任意有则是函数的最大值;
③若存在使得对任意有则是函数的最大值.
这些命题中,真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
(2)已知函数若对恒成立,则的值为
A. B. C . D.
14.什么是函数的零点 函数零点有什么性质 你能正确运用函数零点的性质解决有关方程的根的分布问题吗
练习 函数的零点所在的大致区间是( )
A. B. C. D.
15.你理解导数的几何意义吗 会求经过一点的曲线的切线方程吗 过某点的切线不一定只有一条
如:已知函数(1)求曲线在点处的切线方程;
(2)若过点可作曲线的三条切线,求实数的取值范围.
16.你理解函数的单调性和导数的关系吗 在应用导数研究函数的单调性时,往往需要解含有参数的二次不等式,在进行讨论时,你考虑的全面吗,注意到特殊情况了吗 你是否注意二次项系数为零的情况
如;已知函数,.(Ⅰ)讨论函数的单调区间;
(Ⅱ)设函数在区间内是减函数,求的取值范围.
17。对于形如的复合函数导数的求法,你掌握了吗 这是正确应用导数解决问题的前提.
如:若上是减函数,则的取值范围是( )
A. B. C. D.
18.你理解函数在某点取得极值的必要条件和充分条件吗 函数的导函数,则是为函数极值的必要不充分条件. 给出函数极大(小)值的条件,一定要既考虑,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记。如:设函数,其中.证明:当时,函数没有极值点;当时,函数有且只有一个极值点,并求出极值.
19..在应用导数求参数的范围时,你注意到端点的取舍吗 讨论时遗漏特殊情况了吗
设函数为实数。
(1)已知函数在处取得极值,求的值;
(2)已知不等式对任意都成立,求实数的取值范围。
20.你理解存在性问题和恒成立问题的区别与联系吗 在解题时切不可把二者混为一谈.
遇到含参不等式恒成立求参变量的范围问题,通常采用分离参数法,转化为求某函数的最大值(或最小值);具体地:g(a)>f(x)在x∈A上恒成立 g(a)>f(x)max,g(a)
a≥f(x)恒成立a≥[f(x)]max,;a≤f(x)恒成立a≤[f(x)]min;
如:函数. (1).若关于的不等式有解,则实数的取值范围是 ;(2) 若关于的不等式恒成立,则实数的取值范围是 .
21.几类常见的抽象函数 :
①正比例函数型: ---------------;
②幂函数型: --------------,;
③指数函数型: ----------,;
④对数函数型: ---,;
⑤三角函数型: ----- 。
如:(1)已知是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则__(答:0)
(2)已知是定义在上的奇函数,当时,
的图像如右图所示,那么不等式的解集
是_____________(答:);
精品资源,欢迎下载!!
21世纪教育网~~~K@s%U~~~
21世纪教育网
21世纪教育网
21世纪教育网
y
x
O
y
x
O
y
x
O
y
x
O
A.
B.
C.
D.
O 1 2 3 x
y
同课章节目录
