四年级下册数学课件 三角形的分类 西师大版(16页PPT)
文档属性
| 名称 | 四年级下册数学课件 三角形的分类 西师大版(16页PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 10:50:41 | ||
图片预览


文档简介
(共16张PPT)
课堂引入
下面的角分别是什么角?
锐角
钝角
直角
(等于90°)
(大于0°小于90°)
(大于90°
且小于180°)
课堂引入
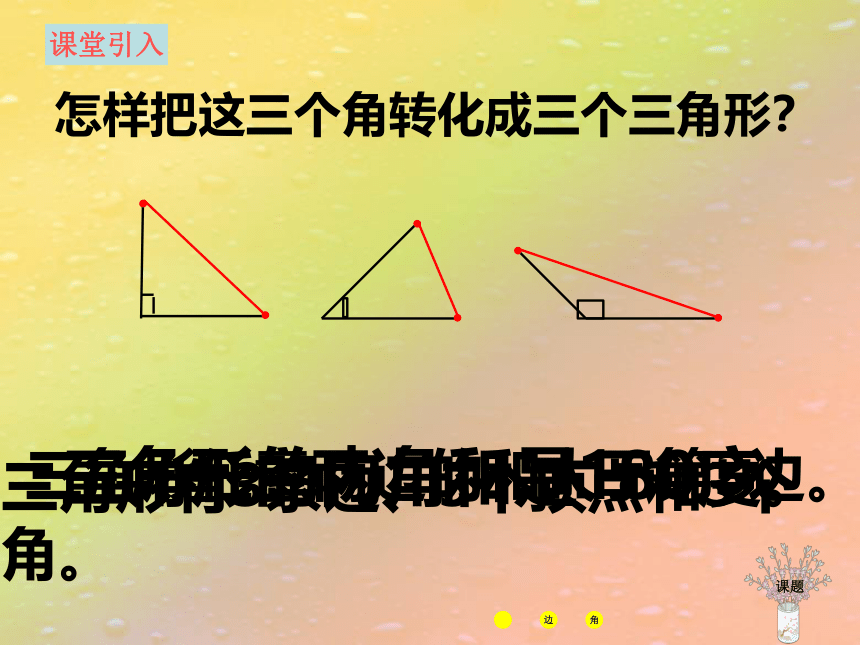
怎样把这三个角转化成三个三角形?
三角形有3条边、3个顶点和3个角。
边
角
三角形任意两边的和大于第3边。
三角形的内角和是180度。
课题
1
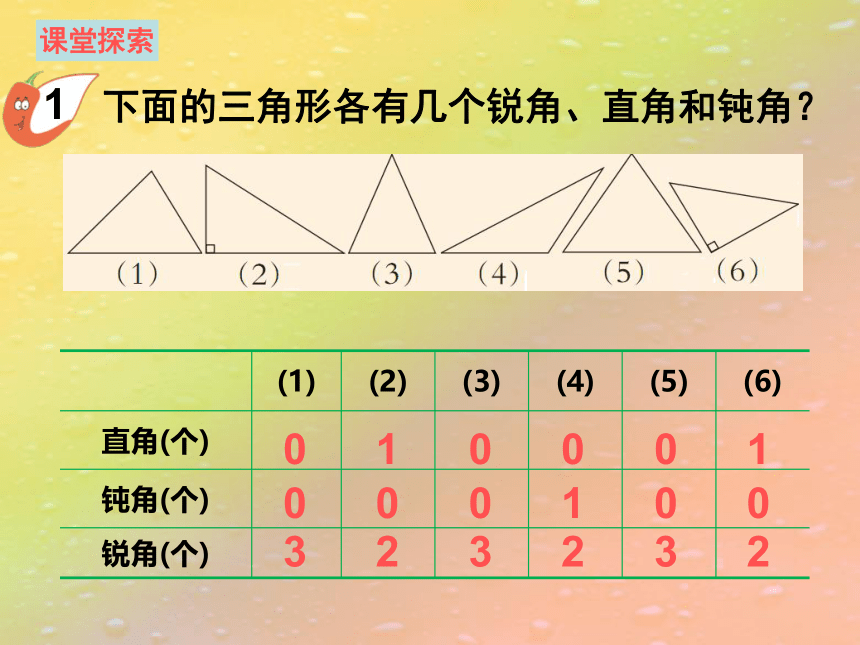
下面的三角形各有几个锐角、直角和钝角?
课堂探索
(1)
(2)
(3)
(4)
(5)
(6)
直角(个)
钝角(个)
锐角(个)
0
0
3
1
0
2
0
0
3
0
1
2
0
0
3
1
0
2
(1)
(2)
(3)
(4)
(5)
(6)
直角(个)
0
1
0
0
0
1
钝角(个)
0
0
0
1
0
0
锐角(个)
3
2
3
2
3
2
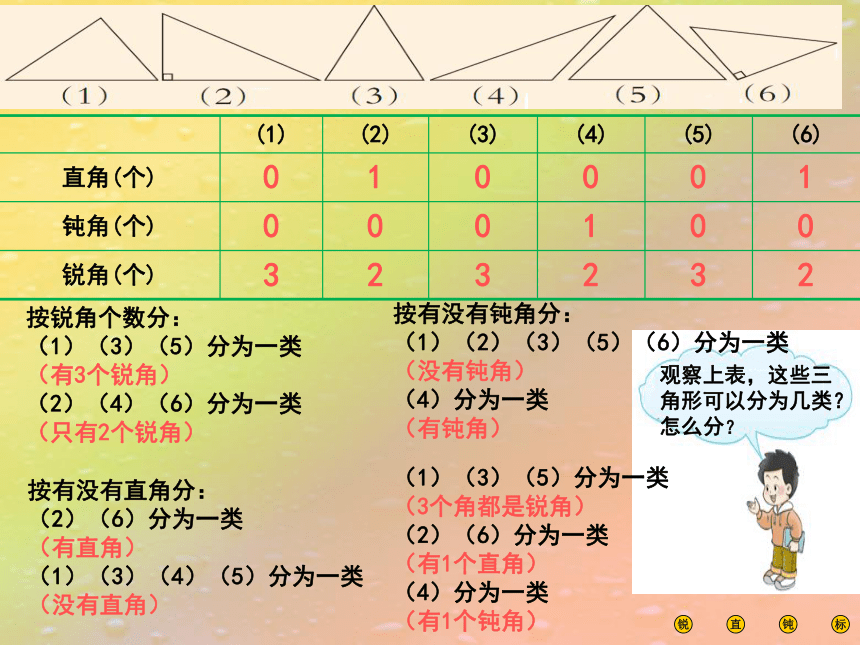
观察上表,这些三角形可以分为几类?怎么分?
按锐角个数分:
(1)(3)(5)分为一类
(有3个锐角)
(2)(4)(6)分为一类
(只有2个锐角)
按有没有直角分:
(2)(6)分为一类
(有直角)
(1)(3)(4)(5)分为一类
(没有直角)
(1)(3)(5)分为一类
(3个角都是锐角)
(2)(6)分为一类
(有1个直角)
(4)分为一类
(有1个钝角)
锐
直
标
按有没有钝角分:
(1)(2)(3)(5)(6)分为一类
(没有钝角)
(4)分为一类
(有钝角)
钝
(1)
(2)
(3)
(4)
(5)
(6)
直角(个)
0
1
0
0
0
1
钝角(个)
0
0
0
1
0
0
锐角(个)
3
2
3
2
3
2
课堂
探索
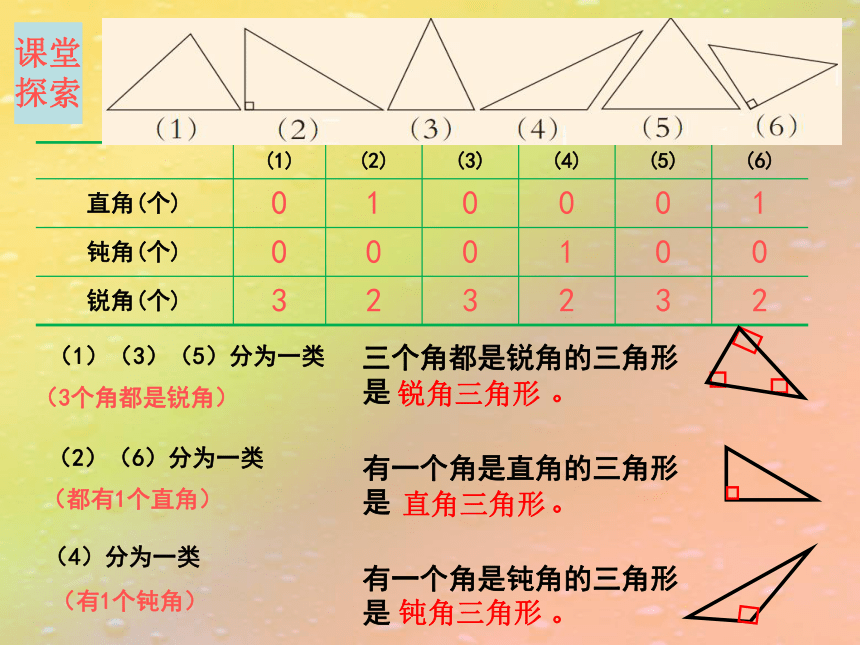
三个角都是锐角的三角形
是
。
有一个角是直角的三角形
是
。
有一个角是钝角的三角形
是
。
(1)(3)(5)分为一类
(3个角都是锐角)
(2)(6)分为一类
(都有1个直角)
(4)分为一类
(有1个钝角)
锐角三角形
直角三角形
钝角三角形
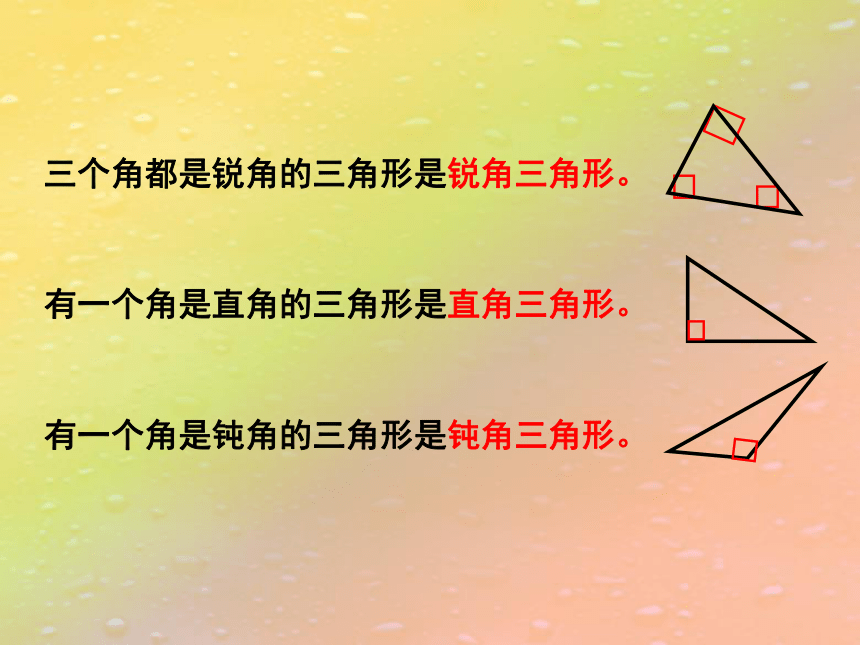
三个角都是锐角的三角形是锐角三角形。
有一个角是直角的三角形是直角三角形。
有一个角是钝角的三角形是钝角三角形。
课堂练习
跳伞(连线)。
怎样才能快速判断出各类三角形?
一个三角形中,它的最大角是什么角,
这个三角形就是什么三角形。
课堂探索
讨论:
因为∠1+∠2=180°,已等于了三角形内角和,所以不能再有第三个角的存在。
在一个三角形里能不能有2个直角?能不能有2个钝角?或1个直角和1个钝角?
1
2
a
b
c
课堂探索
讨论:
在一个三角形里能不能有2个直角?能不能有2个钝角?或1个直角和1个钝角?
因为∠1+∠2
>
180°,已超出三角形内角和,所以不能再有第三个角的存在。
a
b
c
1
2
课堂探索
讨论:
在一个三角形里能不能有2个直角?能不能有2个钝角?或1个直角和1个钝角?
因为∠1+∠2
>
180°,已超出三角形内角和,所以不能再有第三个角的存在。
a
b
c
1
2
课堂探索
锐角三角形
直角三角形
钝角三角形
相同点
不同点(最大角)
名称
填一填,想一想。
至少有两个锐角
最大角是锐角
最大角是直角
最大角是钝角
如果我们把所有的三角形看作一个整体,这个
整体由几部分组成,哪几部分?
课堂探索
钝角三角形
锐角三角形
直角三角形
锐
直
钝
课堂练习
这3个三角形被纸片盖住了一部分。根据露出的三角形的角,判断它们是什么三角形。
钝角三角形
直角三角形
钝角三角形
直角三角形
锐角三角形
可能是
如果露出的角是钝角和直角
如果露出的角是锐角呢
课堂练习
50
。
100
。
60
。
90
。
课堂总结
通过这节课的学习,你学到了什么?
课堂引入
下面的角分别是什么角?
锐角
钝角
直角
(等于90°)
(大于0°小于90°)
(大于90°
且小于180°)
课堂引入
怎样把这三个角转化成三个三角形?
三角形有3条边、3个顶点和3个角。
边
角
三角形任意两边的和大于第3边。
三角形的内角和是180度。
课题
1
下面的三角形各有几个锐角、直角和钝角?
课堂探索
(1)
(2)
(3)
(4)
(5)
(6)
直角(个)
钝角(个)
锐角(个)
0
0
3
1
0
2
0
0
3
0
1
2
0
0
3
1
0
2
(1)
(2)
(3)
(4)
(5)
(6)
直角(个)
0
1
0
0
0
1
钝角(个)
0
0
0
1
0
0
锐角(个)
3
2
3
2
3
2
观察上表,这些三角形可以分为几类?怎么分?
按锐角个数分:
(1)(3)(5)分为一类
(有3个锐角)
(2)(4)(6)分为一类
(只有2个锐角)
按有没有直角分:
(2)(6)分为一类
(有直角)
(1)(3)(4)(5)分为一类
(没有直角)
(1)(3)(5)分为一类
(3个角都是锐角)
(2)(6)分为一类
(有1个直角)
(4)分为一类
(有1个钝角)
锐
直
标
按有没有钝角分:
(1)(2)(3)(5)(6)分为一类
(没有钝角)
(4)分为一类
(有钝角)
钝
(1)
(2)
(3)
(4)
(5)
(6)
直角(个)
0
1
0
0
0
1
钝角(个)
0
0
0
1
0
0
锐角(个)
3
2
3
2
3
2
课堂
探索
三个角都是锐角的三角形
是
。
有一个角是直角的三角形
是
。
有一个角是钝角的三角形
是
。
(1)(3)(5)分为一类
(3个角都是锐角)
(2)(6)分为一类
(都有1个直角)
(4)分为一类
(有1个钝角)
锐角三角形
直角三角形
钝角三角形
三个角都是锐角的三角形是锐角三角形。
有一个角是直角的三角形是直角三角形。
有一个角是钝角的三角形是钝角三角形。
课堂练习
跳伞(连线)。
怎样才能快速判断出各类三角形?
一个三角形中,它的最大角是什么角,
这个三角形就是什么三角形。
课堂探索
讨论:
因为∠1+∠2=180°,已等于了三角形内角和,所以不能再有第三个角的存在。
在一个三角形里能不能有2个直角?能不能有2个钝角?或1个直角和1个钝角?
1
2
a
b
c
课堂探索
讨论:
在一个三角形里能不能有2个直角?能不能有2个钝角?或1个直角和1个钝角?
因为∠1+∠2
>
180°,已超出三角形内角和,所以不能再有第三个角的存在。
a
b
c
1
2
课堂探索
讨论:
在一个三角形里能不能有2个直角?能不能有2个钝角?或1个直角和1个钝角?
因为∠1+∠2
>
180°,已超出三角形内角和,所以不能再有第三个角的存在。
a
b
c
1
2
课堂探索
锐角三角形
直角三角形
钝角三角形
相同点
不同点(最大角)
名称
填一填,想一想。
至少有两个锐角
最大角是锐角
最大角是直角
最大角是钝角
如果我们把所有的三角形看作一个整体,这个
整体由几部分组成,哪几部分?
课堂探索
钝角三角形
锐角三角形
直角三角形
锐
直
钝
课堂练习
这3个三角形被纸片盖住了一部分。根据露出的三角形的角,判断它们是什么三角形。
钝角三角形
直角三角形
钝角三角形
直角三角形
锐角三角形
可能是
如果露出的角是钝角和直角
如果露出的角是锐角呢
课堂练习
50
。
100
。
60
。
90
。
课堂总结
通过这节课的学习,你学到了什么?
