江苏省南京学大教育专修学校2012届高三2月测试数学试题
文档属性
| 名称 | 江苏省南京学大教育专修学校2012届高三2月测试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 269.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-09 00:00:00 | ||
图片预览



文档简介
总分:100分 考试时间:60分钟 学生姓名: _______
校区:_________ 授课教师: 学管老师:
注意事项:
请考生使用蓝色或黑色圆珠笔、签字笔或钢笔作答。
考核内容:
考试范围介绍 高考考纲涉及的范围
涉及知识及考点 函数,三角函数、向量、数列、立体几何、平面解析几何、复数、统计、概率、流程图
成绩统计:
卷Ⅰ 题号 一 二 三 四 总分 总成绩
分数
卷Ⅱ 题号 一 二 三 四 总分
分数
附加卷 一 二 总分
一、填空题(本大题共10题,每题5分,共50分)
1.已知集合,若,则实数a= ▲
2.经过点,与向量垂直的直线方程是 ▲
3.已知复数z满足:,则z= ▲
4.已知向量若A、B、C三点共线,则实数m= ▲
5.函数的周期T= ▲
6.已知点与椭圆的两个焦点构成等腰三角形,则椭圆的离心率e= ▲
7.设为两个不重合的平面,是不重合的直线,给出下列命题,其中正确的序号是 ▲
① 若则∥;② 若相交不垂直,则n与m不垂直;③ 若,则;④ m是平面的斜线,n是m在平面内的射影,若,则.
8.设点P是曲线上的任意一点,则点P到直线的最小距离为 ▲
9.在中,,则角B= ▲
10.通项公式为的数列,若满足,且对恒成立,则实数a的取值范围是 ▲
二、解答题(本大题共4题,共50分,其中11和12各10分,13和14各15分)
11.已知函数,其中,的图象与直线的交点的横坐标成公差为的等差数列
⑴求的解析式;⑵若在中,,,求的面积.
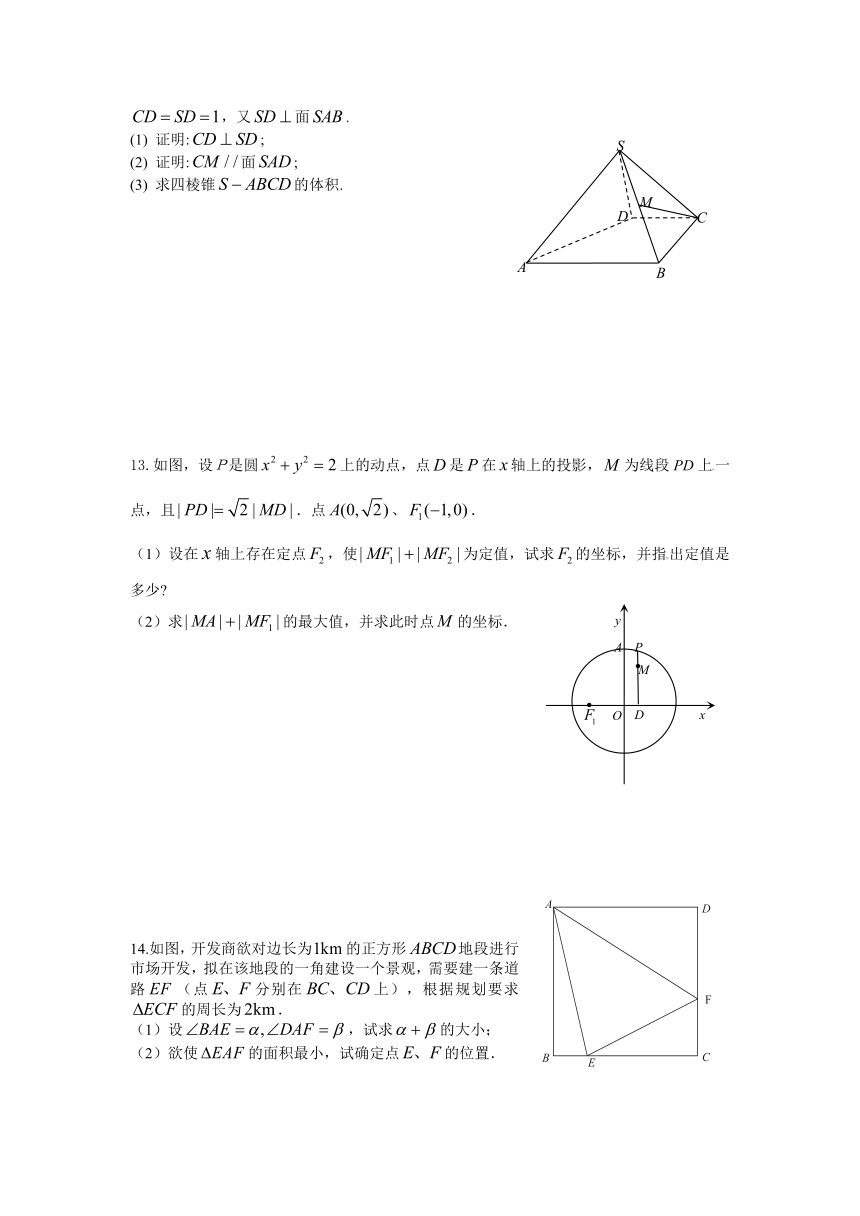
12.如图,四棱锥中,是的中点,,,且,,又面.
(1) 证明:;
(2) 证明:面;
(3) 求四棱锥的体积.
13.如图,设P是圆上的动点,点是在轴上的投影,为线段PD上一点,且.点、.
(1)设在轴上存在定点,使为定值,试求的坐标,并指出定值是多少
(2)求的最大值,并求此时点的坐标.
14.如图,开发商欲对边长为的正方形地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路(点分别在上),根据规划要求的周长为.
(1)设,试求的大小;
(2)欲使的面积最小,试确定点的位置.
理科附加卷(20分)(时间15分钟)
1.将曲线绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.
2.已知圆C的极坐标方程是,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线的参数方程是(t是参数)。若直线与圆C相切,求实数m的值。
试卷配套属性表
考查点 涉及该考查点的题号 总分 优秀 良好 有较大提高空间
集合与函数 3、9、10、14 31 28--31 22--28 0--22
三角与向量 2、5、11 24 19--24 16--19 0--16
平面几何立体几何 12、13 30 24--30 21--24 0--21
数列 8 5 5 5 0
概率统计复数流程图 1、4、6、7 20 20 15 0--15
试卷配套答案
2012年南京学大2月月测试卷参考答案
1、;2、;3、;4、m=-1;5、;6、;
7、③;8、;9 、 或 ;10、
13.(1)设点M的坐标是,P的坐标是
因为点D是P在轴上投影,为PD上一点,由条件得:,且---2f
∵在圆上,∴,整理得,
即M轨迹是以为焦点的椭圆
由椭圆的定义可知,
(2)由(1)知,
当三点共线,且在延长线上时,取等号.
直线,联立,
其中,解得
即所求的的坐标是.
14.(1)设,,
则,由已知得:,
即
,即
(2)由(1)知,
=
=.
,,即时的面积最小,最小面积为.
,故此时
所以,当时,的面积最小.
附加题答案
S
A
B
C
D
M
x
y
P
M
O
D
A
x
y
P
M
O
D
A
校区:_________ 授课教师: 学管老师:
注意事项:
请考生使用蓝色或黑色圆珠笔、签字笔或钢笔作答。
考核内容:
考试范围介绍 高考考纲涉及的范围
涉及知识及考点 函数,三角函数、向量、数列、立体几何、平面解析几何、复数、统计、概率、流程图
成绩统计:
卷Ⅰ 题号 一 二 三 四 总分 总成绩
分数
卷Ⅱ 题号 一 二 三 四 总分
分数
附加卷 一 二 总分
一、填空题(本大题共10题,每题5分,共50分)
1.已知集合,若,则实数a= ▲
2.经过点,与向量垂直的直线方程是 ▲
3.已知复数z满足:,则z= ▲
4.已知向量若A、B、C三点共线,则实数m= ▲
5.函数的周期T= ▲
6.已知点与椭圆的两个焦点构成等腰三角形,则椭圆的离心率e= ▲
7.设为两个不重合的平面,是不重合的直线,给出下列命题,其中正确的序号是 ▲
① 若则∥;② 若相交不垂直,则n与m不垂直;③ 若,则;④ m是平面的斜线,n是m在平面内的射影,若,则.
8.设点P是曲线上的任意一点,则点P到直线的最小距离为 ▲
9.在中,,则角B= ▲
10.通项公式为的数列,若满足,且对恒成立,则实数a的取值范围是 ▲
二、解答题(本大题共4题,共50分,其中11和12各10分,13和14各15分)
11.已知函数,其中,的图象与直线的交点的横坐标成公差为的等差数列
⑴求的解析式;⑵若在中,,,求的面积.
12.如图,四棱锥中,是的中点,,,且,,又面.
(1) 证明:;
(2) 证明:面;
(3) 求四棱锥的体积.
13.如图,设P是圆上的动点,点是在轴上的投影,为线段PD上一点,且.点、.
(1)设在轴上存在定点,使为定值,试求的坐标,并指出定值是多少
(2)求的最大值,并求此时点的坐标.
14.如图,开发商欲对边长为的正方形地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路(点分别在上),根据规划要求的周长为.
(1)设,试求的大小;
(2)欲使的面积最小,试确定点的位置.
理科附加卷(20分)(时间15分钟)
1.将曲线绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.
2.已知圆C的极坐标方程是,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线的参数方程是(t是参数)。若直线与圆C相切,求实数m的值。
试卷配套属性表
考查点 涉及该考查点的题号 总分 优秀 良好 有较大提高空间
集合与函数 3、9、10、14 31 28--31 22--28 0--22
三角与向量 2、5、11 24 19--24 16--19 0--16
平面几何立体几何 12、13 30 24--30 21--24 0--21
数列 8 5 5 5 0
概率统计复数流程图 1、4、6、7 20 20 15 0--15
试卷配套答案
2012年南京学大2月月测试卷参考答案
1、;2、;3、;4、m=-1;5、;6、;
7、③;8、;9 、 或 ;10、
13.(1)设点M的坐标是,P的坐标是
因为点D是P在轴上投影,为PD上一点,由条件得:,且---2f
∵在圆上,∴,整理得,
即M轨迹是以为焦点的椭圆
由椭圆的定义可知,
(2)由(1)知,
当三点共线,且在延长线上时,取等号.
直线,联立,
其中,解得
即所求的的坐标是.
14.(1)设,,
则,由已知得:,
即
,即
(2)由(1)知,
=
=.
,,即时的面积最小,最小面积为.
,故此时
所以,当时,的面积最小.
附加题答案
S
A
B
C
D
M
x
y
P
M
O
D
A
x
y
P
M
O
D
A
同课章节目录
