2.2 法拉第电磁感应定律—【新教材】人教版(2019)高中物理选择性必修第二册同步检测(Word含答案)
文档属性
| 名称 | 2.2 法拉第电磁感应定律—【新教材】人教版(2019)高中物理选择性必修第二册同步检测(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 202.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-15 00:00:00 | ||
图片预览


文档简介
2.2法拉第电磁感应定律
一、单选题
关于感应电动势的大小,下列说法中正确的是(????)
A. 线圈中磁通量越大,产生的感应电动势一定越大
B. 线圈中磁通量变化越大,产生的感应电动势一定越大
C. 线圈中磁通量变化越快,产生的感应电动势一定越大
D. 线圈所在处磁感应强度越大,产生的感应电动势一定越大
一个单匝线圈的磁通量始终为每秒钟均匀地增加2Wb,则(????)
A. 线圈中的感应电动势每秒钟增加2V
B. 线圈中的感应电动势每秒钟减少2V
C. 线圈中的感应电动势始终为2V
D. 线圈中不产生感应电动势
如图所示,圆环a和圆环b半径之比为2∶1,两环用同样粗细的、同种材料的导线连成闭合回路,连接两圆环的导线电阻不计,匀强磁场的磁感强度变化率恒定,则在a环单独置于磁场中和b环单独置于磁场中两种情况下,M、N两点的电势差之比为(????)
A. 1∶2 B. 2∶1 C. 1∶4 D. 4∶1
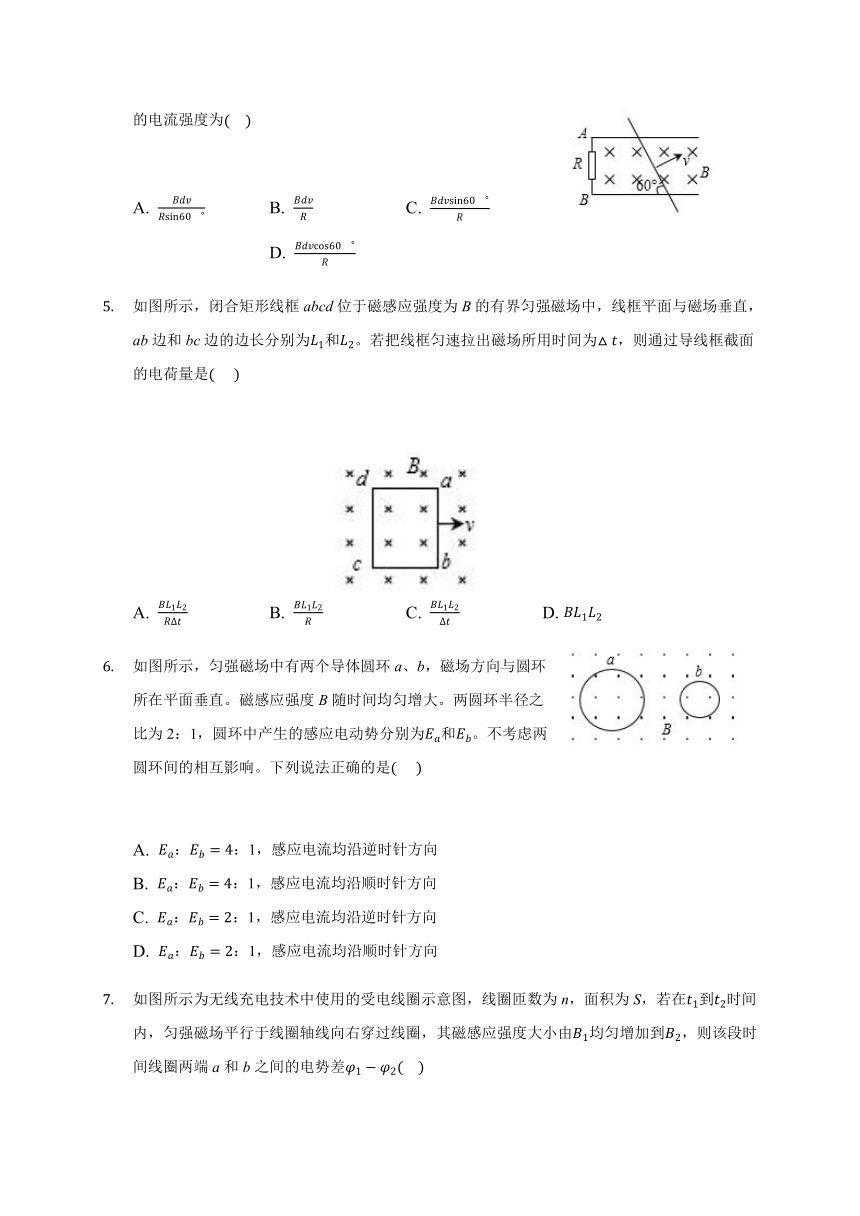
如图所示,磁感应强度为B的匀强磁场中,有间距为d的两平行金属导轨,两导轨间连接一阻值为R的电阻,磁场方向垂直于平行导轨所在平面。一根长直金属棒与导轨成60°角放置,且接触良好,则当金属棒以垂直于棒的恒定速度v沿金属导轨滑行时,其它电阻不计,电阻R中的电流强度为(????)
A. BdvRsin60? B. BdvR C. Bdvsin60?R D. Bdvcos60?R
如图所示,闭合矩形线框abcd位于磁感应强度为B的有界匀强磁场中,线框平面与磁场垂直,ab边和bc边的边长分别为L1和L2。若把线框匀速拉出磁场所用时间为△t,则通过导线框截面的电荷量是(??? )
A. BL1L2RΔt B. BL1L2R C. BL1L2Δt D. BL1L2
如图所示,匀强磁场中有两个导体圆环a、b,磁场方向与圆环所在平面垂直。磁感应强度B随时间均匀增大。两圆环半径之比为2:1,圆环中产生的感应电动势分别为Ea和Eb。不考虑两圆环间的相互影响。下列说法正确的是(??? )
A. Ea:Eb=4:1,感应电流均沿逆时针方向
B. Ea:Eb=4:1,感应电流均沿顺时针方向
C. Ea:Eb=2:1,感应电流均沿逆时针方向
D. Ea:Eb=2:1,感应电流均沿顺时针方向
如图所示为无线充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φ1?φ2(? ?)
A. 恒为nS(B2?B1)(t2?t1) B. 从0均匀变化到nS(B2?B1)(t2?t1)
C. 恒为?nS(B2?B1)(t2?t1) D. 从0均匀变化到?nS(B2?B1)(t2?t1)
如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻R。金属棒ab与两导轨垂直并保持良好接触,整个装置放在匀强磁场中,磁场方向垂直于导轨平面向下。现使磁感应强度随时间均匀减小,ab始终保持静止,下列说法正确的是(????)
A. ab中的感应电流方向由b到a B. ab中的感应电流逐渐减小
C. ab所受的安培力保持不变 D. ab所受的静摩擦力逐渐减小
二、多选题
一个N匝圆形线圈,放在磁感应强度为B的匀强磁场中,线圈平面与磁感应强度方向成30°角,磁感应强度随时间均匀变化,线圈导线规格不变,下列方法中可使线圈中感应电流增加一倍的是(????)
A. 只将线圈匝数增加一倍
B. 只将线圈面积增加一倍
C. 只将线圈半径增加一倍
D. 只将线圈平面转至跟磁感线垂直的位置
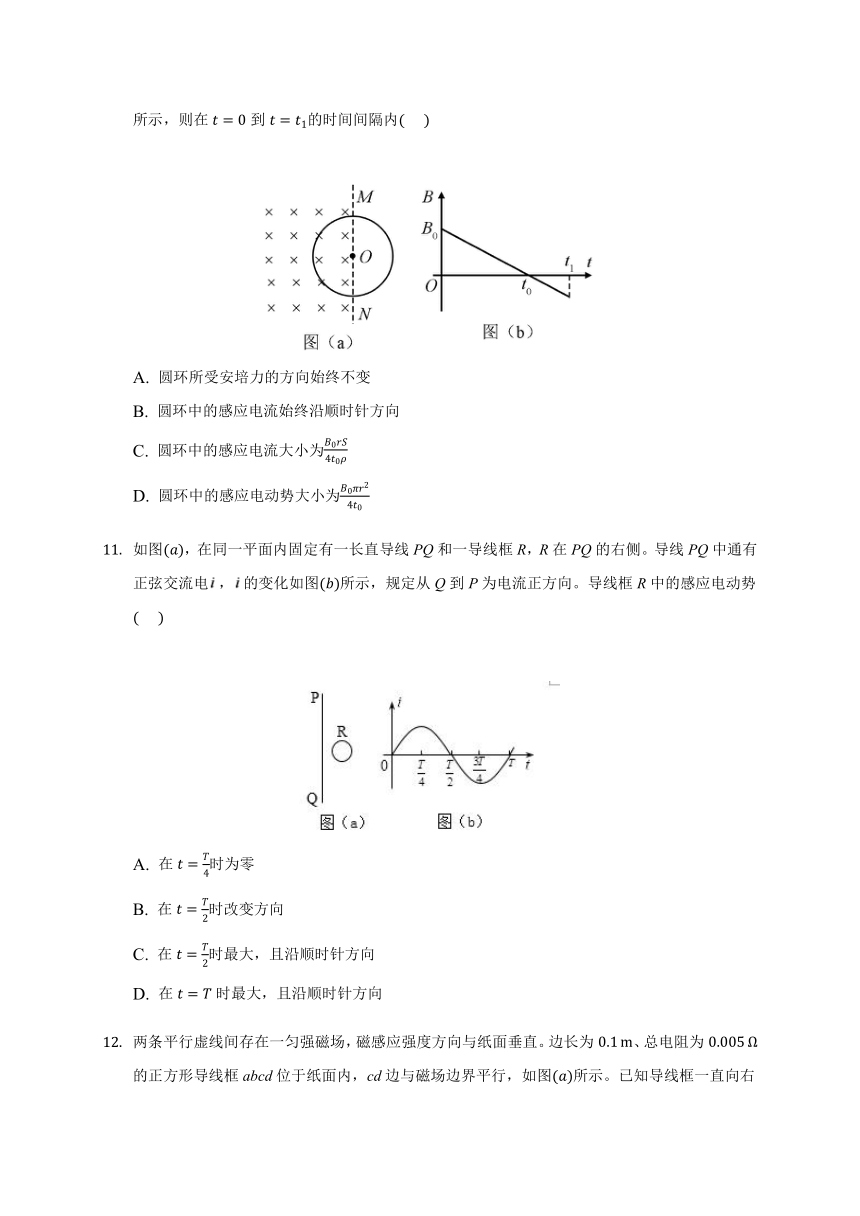
空间存在一方向与直面垂直、大小随时间变化的匀强磁场,其边界如图(a)中虚线MN所示,一硬质细导线的电阻率为ρ、横截面积为S,将该导线做成半径为r的圆环固定在纸面内,圆心O在MN上。t=0时磁感应强度的方向如图(a)所示。磁感应强度B随时间t的变化关系如图(b)所示,则在t=0到t=t1的时间间隔内(??? )
A. 圆环所受安培力的方向始终不变
B. 圆环中的感应电流始终沿顺时针方向
C. 圆环中的感应电流大小为B0rS4t0ρ
D. 圆环中的感应电动势大小为B0πr24t0
如图(a),在同一平面内固定有一长直导线PQ和一导线框R,R在PQ的右侧。导线PQ中通有正弦交流电,的变化如图(b)所示,规定从Q到P为电流正方向。导线框R中的感应电动势(??? )
A. 在t=T4时为零
B. 在t=T2时改变方向
C. 在t=T2时最大,且沿顺时针方向
D. 在t=T时最大,且沿顺时针方向
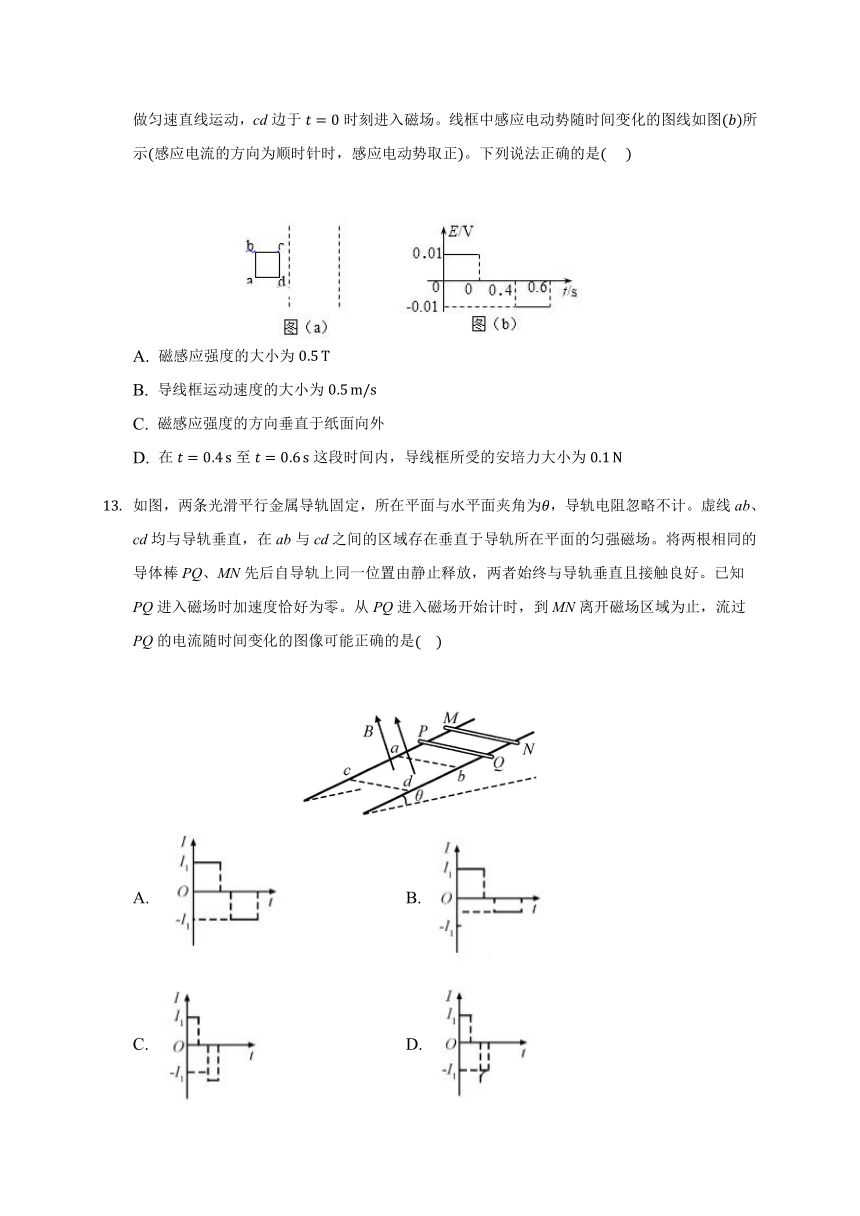
两条平行虚线间存在一匀强磁场,磁感应强度方向与纸面垂直。边长为0.1?m、总电阻为0.005?Ω的正方形导线框abcd位于纸面内,cd边与磁场边界平行,如图(a)所示。已知导线框一直向右做匀速直线运动,cd边于t=0时刻进入磁场。线框中感应电动势随时间变化的图线如图(b)所示(感应电流的方向为顺时针时,感应电动势取正)。下列说法正确的是(??? )
A. 磁感应强度的大小为0.5?T
B. 导线框运动速度的大小为0.5?m/s
C. 磁感应强度的方向垂直于纸面向外
D. 在t=0.4?s至t=0.6?s这段时间内,导线框所受的安培力大小为0.1?N
如图,两条光滑平行金属导轨固定,所在平面与水平面夹角为θ,导轨电阻忽略不计。虚线ab、cd均与导轨垂直,在ab与cd之间的区域存在垂直于导轨所在平面的匀强磁场。将两根相同的导体棒PQ、MN先后自导轨上同一位置由静止释放,两者始终与导轨垂直且接触良好。已知PQ进入磁场时加速度恰好为零。从PQ进入磁场开始计时,到MN离开磁场区域为止,流过PQ的电流随时间变化的图像可能正确的是(????)
A. B.
C. D.
三、填空题
如图所示,从匀强磁场中用外力把一矩形线圈匀速拉出磁场区域。如果两次拉出的速度之比v1∶v2=1∶2,则在将线圈拉出磁场区域的过程中,两次所用的外力大小之比F1∶F2=______________,线圈中产生的焦耳热之比Q1∶Q2=______________,通过线圈某截面的电荷量之比q1∶q2=______________。
单匝边长为20cm的正方形导线框,在磁感应强度为0.2T的匀强磁场中围绕与磁感应强度方向垂直的转轴匀速转动,转速为120r/min。当线框从平行于磁场位置开始转过90°时,线圈中磁通量的变化量是________,线圈中磁通量平均变化率为________,平均感应电动势为________。
A、B两闭合线圈用同样导线绕成,且均为10匝,线圈半径rA=2rB,线圈B内有如图所示的有理想边界的匀强磁场。若磁场均匀减小,则A、B中的感应电动势之比EA∶EB=__________,产生的感应电流之比IA∶IB=__________。
一导体棒长40cm,在磁感应强度为0.1T的匀强磁场中做切割磁感线运动,运动速度为5.0m/s,若速度方向与磁感线方向夹角为30°,则导体棒中感应电动势的大小为_______V。此导体棒在做切割磁感线运动时,若速度大小不变,可能产生的最大感应电动势为___________V。
四、计算题
如图所示,两根足够长的平行导轨,间距L?=0.3?m,在导轨间有垂直纸面向里的匀强磁场,磁感应强度B?=?0.5?T。导轨左侧接有R=4Ω的定值电阻。一根直金属杆MN以v=?2?m/s的速度向右匀速运动,杆MN始终与导轨垂直且接触良好。杆MN的电阻r=1Ω,导轨的电阻可忽略。求杆MN中产生的感应电动势E及a、b两点间的电势差Uab。
如图所示,固定于水平面上的金属框架abcd,处在竖直向下的匀强磁场中。金属棒MN沿框架以速度v向右做匀速运动。框架的ab与dc平行,bc与ab、dc垂直。MN与bc的长度均为l,在运动过程中MN始终与bc平行,且与框架保持良好接触。磁场的磁感应强度为B。请根据法拉第电磁感应定律E=ΔΦΔt,推导金属棒MN中的感应电动势E。
如图所示,U形导线框MNQP水平放置在磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为L=0.5m,横跨在导线框上的导体棒ab的质量m=0.1kg,电阻r=1.0Ω,接在NQ间的电阻R=4.0Ω,电压表为理想电表,其余电阻不计。若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦。求:
(1)通过导体棒ab的电流大小和方向;
(2)电压表的示数;
(3)若某一时刻撤去水平外力,则从该时刻起,在导体棒的运动的过程中,回路中产生的热量。
如图甲所示,一个电阻值为R的圆形金属线圈与阻值为2R的电阻R1连接成闭合回路。线圈的半径为r。在线圈中存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系如图乙所示,图中B0和t0已知。导线电阻不计。求:0至t0时间内,
(1)通过电阻R1电流I的大小和方向;
(2)通过电阻R1的电荷量q;
(3)电阻R1上产生的热量Q。
导体切割磁感线的运动可以从宏观和微观两个角度来认识。如图所示,固定于水平面的U形导线框处于竖直向下的匀强磁场中,金属直导线MN在与其垂直的水平恒力F作用下,在导线框上以速度v做匀速运动,速度v与恒力F方向相同;导线MN始终与导线框形成闭合电路。已知导线MN电阻为R,其长度L恰好等于平行轨道间距,磁场的磁感应强度为B。忽略摩擦阻力和导线框的电阻。通过公式推导验证:在Δ?t时间内,F对导线MN所做的功W等于电路获得的电能W电,也等于导线MN中产生的焦耳热Q。
均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m。将其置于磁感强度为B的水平匀强磁场上方h处,如图所示。线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界面平行。当cd边刚进入磁场时,
(1)求线框中产生的感应电动势大小;
(2)求cd两点间的电势差大小;
(3)若此时线框加速度恰好为零,求线框下落的高度h所应满足的条件。
答案和解析
1. C 2. C 3. B 4. A 5. B 6. B 7. C 8. D 9. CD 10. BC 11. AC 12. BC
13. AD
14. 1:2;1:2;1:1
15. 8×10?3?Wb;6.4×10?2?Wb/s;0.064?V
16. 1:1;1:2
17. 0.1;0.2
18.解:杆MN做切割磁感线的运动?E=BLv? ? ? ? ? ? ? ? ??
产生的感应电动势:E=0.3V
?Uab=45E=0.24V
19.解:如图所示,在一小段时间Δt内,金属棒MN的位移Δx=vΔt
?
这个过程中线框的面积的变化量ΔS=lΔx=lvΔt?
穿过闭合电路的磁通量的变化量ΔΦ=BΔS=BlvΔt?
根据法拉第电磁感应定律:E=ΔΦΔt??
解得:E=Blv??
20.解:(1)感应电动势为E=BLv=0.2V??????????????????????????????
感应电流为:I=ER+r=0.25A=0.04A?????????????????????
由右手定则判断通过导体棒的电流方向为b到a??????????????
(2)电压表的示数为:U=IR=0.16V???????????????????????????
(3)撤去水平拉力后,导体棒作减速运动
根据能量守恒:Q=12mv2=?0.2J????????????????????????
回路中产生的热量为0.2J? ?????
21.解:(1)根据法拉第电磁感应定律有
所以I=ER+2R=B0πr23Rt0???????????????????????????????????????????
根据楞次定律:通过R1的电流方向为a→b?????????????????????????
(2)设通过R1的电量为q,则有q=It0=B0πr23R?????????????????????????????????????????
(3)根据焦耳定律Q=I2R1t0=2Rt0B0πr23Rt02=2B02π2r49Rt0??????????????
22.解:电动势E=BLv
导线匀速运动,受力平衡?F=F安=BIL
在Δ?t时间内,外力F对导线做功W=FvΔ?t=F安vΔ?t=BILvΔ?t
电路获得的电能W电=qE=IEΔ?t=BILvΔ?t
可见,F对导线MN所做的功等于电路获得的电能W电;
导线MN中产生的焦耳热Q=I2RΔ?t=IΔ?t×IR=qE=W电
可见,电路获得的电能W电等于导线MN中产生的焦耳热Q。
23.解:(1)cd边刚进入磁场时,线框速度v=2g?
线框中产生的感应电动势:E=BLv=BL2g?
(2)此时线框中电流:I=ER?
cd两点间的电势差U=I(34R)=34E=34BL2g?
(3)安培力F=BIL=B2L22g?R
根据牛顿第二定律mg?F=ma,由a=0
解得下落高度满足:??=m2gR22B4L4
一、单选题
关于感应电动势的大小,下列说法中正确的是(????)
A. 线圈中磁通量越大,产生的感应电动势一定越大
B. 线圈中磁通量变化越大,产生的感应电动势一定越大
C. 线圈中磁通量变化越快,产生的感应电动势一定越大
D. 线圈所在处磁感应强度越大,产生的感应电动势一定越大
一个单匝线圈的磁通量始终为每秒钟均匀地增加2Wb,则(????)
A. 线圈中的感应电动势每秒钟增加2V
B. 线圈中的感应电动势每秒钟减少2V
C. 线圈中的感应电动势始终为2V
D. 线圈中不产生感应电动势
如图所示,圆环a和圆环b半径之比为2∶1,两环用同样粗细的、同种材料的导线连成闭合回路,连接两圆环的导线电阻不计,匀强磁场的磁感强度变化率恒定,则在a环单独置于磁场中和b环单独置于磁场中两种情况下,M、N两点的电势差之比为(????)
A. 1∶2 B. 2∶1 C. 1∶4 D. 4∶1
如图所示,磁感应强度为B的匀强磁场中,有间距为d的两平行金属导轨,两导轨间连接一阻值为R的电阻,磁场方向垂直于平行导轨所在平面。一根长直金属棒与导轨成60°角放置,且接触良好,则当金属棒以垂直于棒的恒定速度v沿金属导轨滑行时,其它电阻不计,电阻R中的电流强度为(????)
A. BdvRsin60? B. BdvR C. Bdvsin60?R D. Bdvcos60?R
如图所示,闭合矩形线框abcd位于磁感应强度为B的有界匀强磁场中,线框平面与磁场垂直,ab边和bc边的边长分别为L1和L2。若把线框匀速拉出磁场所用时间为△t,则通过导线框截面的电荷量是(??? )
A. BL1L2RΔt B. BL1L2R C. BL1L2Δt D. BL1L2
如图所示,匀强磁场中有两个导体圆环a、b,磁场方向与圆环所在平面垂直。磁感应强度B随时间均匀增大。两圆环半径之比为2:1,圆环中产生的感应电动势分别为Ea和Eb。不考虑两圆环间的相互影响。下列说法正确的是(??? )
A. Ea:Eb=4:1,感应电流均沿逆时针方向
B. Ea:Eb=4:1,感应电流均沿顺时针方向
C. Ea:Eb=2:1,感应电流均沿逆时针方向
D. Ea:Eb=2:1,感应电流均沿顺时针方向
如图所示为无线充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φ1?φ2(? ?)
A. 恒为nS(B2?B1)(t2?t1) B. 从0均匀变化到nS(B2?B1)(t2?t1)
C. 恒为?nS(B2?B1)(t2?t1) D. 从0均匀变化到?nS(B2?B1)(t2?t1)
如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻R。金属棒ab与两导轨垂直并保持良好接触,整个装置放在匀强磁场中,磁场方向垂直于导轨平面向下。现使磁感应强度随时间均匀减小,ab始终保持静止,下列说法正确的是(????)
A. ab中的感应电流方向由b到a B. ab中的感应电流逐渐减小
C. ab所受的安培力保持不变 D. ab所受的静摩擦力逐渐减小
二、多选题
一个N匝圆形线圈,放在磁感应强度为B的匀强磁场中,线圈平面与磁感应强度方向成30°角,磁感应强度随时间均匀变化,线圈导线规格不变,下列方法中可使线圈中感应电流增加一倍的是(????)
A. 只将线圈匝数增加一倍
B. 只将线圈面积增加一倍
C. 只将线圈半径增加一倍
D. 只将线圈平面转至跟磁感线垂直的位置
空间存在一方向与直面垂直、大小随时间变化的匀强磁场,其边界如图(a)中虚线MN所示,一硬质细导线的电阻率为ρ、横截面积为S,将该导线做成半径为r的圆环固定在纸面内,圆心O在MN上。t=0时磁感应强度的方向如图(a)所示。磁感应强度B随时间t的变化关系如图(b)所示,则在t=0到t=t1的时间间隔内(??? )
A. 圆环所受安培力的方向始终不变
B. 圆环中的感应电流始终沿顺时针方向
C. 圆环中的感应电流大小为B0rS4t0ρ
D. 圆环中的感应电动势大小为B0πr24t0
如图(a),在同一平面内固定有一长直导线PQ和一导线框R,R在PQ的右侧。导线PQ中通有正弦交流电,的变化如图(b)所示,规定从Q到P为电流正方向。导线框R中的感应电动势(??? )
A. 在t=T4时为零
B. 在t=T2时改变方向
C. 在t=T2时最大,且沿顺时针方向
D. 在t=T时最大,且沿顺时针方向
两条平行虚线间存在一匀强磁场,磁感应强度方向与纸面垂直。边长为0.1?m、总电阻为0.005?Ω的正方形导线框abcd位于纸面内,cd边与磁场边界平行,如图(a)所示。已知导线框一直向右做匀速直线运动,cd边于t=0时刻进入磁场。线框中感应电动势随时间变化的图线如图(b)所示(感应电流的方向为顺时针时,感应电动势取正)。下列说法正确的是(??? )
A. 磁感应强度的大小为0.5?T
B. 导线框运动速度的大小为0.5?m/s
C. 磁感应强度的方向垂直于纸面向外
D. 在t=0.4?s至t=0.6?s这段时间内,导线框所受的安培力大小为0.1?N
如图,两条光滑平行金属导轨固定,所在平面与水平面夹角为θ,导轨电阻忽略不计。虚线ab、cd均与导轨垂直,在ab与cd之间的区域存在垂直于导轨所在平面的匀强磁场。将两根相同的导体棒PQ、MN先后自导轨上同一位置由静止释放,两者始终与导轨垂直且接触良好。已知PQ进入磁场时加速度恰好为零。从PQ进入磁场开始计时,到MN离开磁场区域为止,流过PQ的电流随时间变化的图像可能正确的是(????)
A. B.
C. D.
三、填空题
如图所示,从匀强磁场中用外力把一矩形线圈匀速拉出磁场区域。如果两次拉出的速度之比v1∶v2=1∶2,则在将线圈拉出磁场区域的过程中,两次所用的外力大小之比F1∶F2=______________,线圈中产生的焦耳热之比Q1∶Q2=______________,通过线圈某截面的电荷量之比q1∶q2=______________。
单匝边长为20cm的正方形导线框,在磁感应强度为0.2T的匀强磁场中围绕与磁感应强度方向垂直的转轴匀速转动,转速为120r/min。当线框从平行于磁场位置开始转过90°时,线圈中磁通量的变化量是________,线圈中磁通量平均变化率为________,平均感应电动势为________。
A、B两闭合线圈用同样导线绕成,且均为10匝,线圈半径rA=2rB,线圈B内有如图所示的有理想边界的匀强磁场。若磁场均匀减小,则A、B中的感应电动势之比EA∶EB=__________,产生的感应电流之比IA∶IB=__________。
一导体棒长40cm,在磁感应强度为0.1T的匀强磁场中做切割磁感线运动,运动速度为5.0m/s,若速度方向与磁感线方向夹角为30°,则导体棒中感应电动势的大小为_______V。此导体棒在做切割磁感线运动时,若速度大小不变,可能产生的最大感应电动势为___________V。
四、计算题
如图所示,两根足够长的平行导轨,间距L?=0.3?m,在导轨间有垂直纸面向里的匀强磁场,磁感应强度B?=?0.5?T。导轨左侧接有R=4Ω的定值电阻。一根直金属杆MN以v=?2?m/s的速度向右匀速运动,杆MN始终与导轨垂直且接触良好。杆MN的电阻r=1Ω,导轨的电阻可忽略。求杆MN中产生的感应电动势E及a、b两点间的电势差Uab。
如图所示,固定于水平面上的金属框架abcd,处在竖直向下的匀强磁场中。金属棒MN沿框架以速度v向右做匀速运动。框架的ab与dc平行,bc与ab、dc垂直。MN与bc的长度均为l,在运动过程中MN始终与bc平行,且与框架保持良好接触。磁场的磁感应强度为B。请根据法拉第电磁感应定律E=ΔΦΔt,推导金属棒MN中的感应电动势E。
如图所示,U形导线框MNQP水平放置在磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为L=0.5m,横跨在导线框上的导体棒ab的质量m=0.1kg,电阻r=1.0Ω,接在NQ间的电阻R=4.0Ω,电压表为理想电表,其余电阻不计。若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦。求:
(1)通过导体棒ab的电流大小和方向;
(2)电压表的示数;
(3)若某一时刻撤去水平外力,则从该时刻起,在导体棒的运动的过程中,回路中产生的热量。
如图甲所示,一个电阻值为R的圆形金属线圈与阻值为2R的电阻R1连接成闭合回路。线圈的半径为r。在线圈中存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系如图乙所示,图中B0和t0已知。导线电阻不计。求:0至t0时间内,
(1)通过电阻R1电流I的大小和方向;
(2)通过电阻R1的电荷量q;
(3)电阻R1上产生的热量Q。
导体切割磁感线的运动可以从宏观和微观两个角度来认识。如图所示,固定于水平面的U形导线框处于竖直向下的匀强磁场中,金属直导线MN在与其垂直的水平恒力F作用下,在导线框上以速度v做匀速运动,速度v与恒力F方向相同;导线MN始终与导线框形成闭合电路。已知导线MN电阻为R,其长度L恰好等于平行轨道间距,磁场的磁感应强度为B。忽略摩擦阻力和导线框的电阻。通过公式推导验证:在Δ?t时间内,F对导线MN所做的功W等于电路获得的电能W电,也等于导线MN中产生的焦耳热Q。
均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m。将其置于磁感强度为B的水平匀强磁场上方h处,如图所示。线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界面平行。当cd边刚进入磁场时,
(1)求线框中产生的感应电动势大小;
(2)求cd两点间的电势差大小;
(3)若此时线框加速度恰好为零,求线框下落的高度h所应满足的条件。
答案和解析
1. C 2. C 3. B 4. A 5. B 6. B 7. C 8. D 9. CD 10. BC 11. AC 12. BC
13. AD
14. 1:2;1:2;1:1
15. 8×10?3?Wb;6.4×10?2?Wb/s;0.064?V
16. 1:1;1:2
17. 0.1;0.2
18.解:杆MN做切割磁感线的运动?E=BLv? ? ? ? ? ? ? ? ??
产生的感应电动势:E=0.3V
?Uab=45E=0.24V
19.解:如图所示,在一小段时间Δt内,金属棒MN的位移Δx=vΔt
?
这个过程中线框的面积的变化量ΔS=lΔx=lvΔt?
穿过闭合电路的磁通量的变化量ΔΦ=BΔS=BlvΔt?
根据法拉第电磁感应定律:E=ΔΦΔt??
解得:E=Blv??
20.解:(1)感应电动势为E=BLv=0.2V??????????????????????????????
感应电流为:I=ER+r=0.25A=0.04A?????????????????????
由右手定则判断通过导体棒的电流方向为b到a??????????????
(2)电压表的示数为:U=IR=0.16V???????????????????????????
(3)撤去水平拉力后,导体棒作减速运动
根据能量守恒:Q=12mv2=?0.2J????????????????????????
回路中产生的热量为0.2J? ?????
21.解:(1)根据法拉第电磁感应定律有
所以I=ER+2R=B0πr23Rt0???????????????????????????????????????????
根据楞次定律:通过R1的电流方向为a→b?????????????????????????
(2)设通过R1的电量为q,则有q=It0=B0πr23R?????????????????????????????????????????
(3)根据焦耳定律Q=I2R1t0=2Rt0B0πr23Rt02=2B02π2r49Rt0??????????????
22.解:电动势E=BLv
导线匀速运动,受力平衡?F=F安=BIL
在Δ?t时间内,外力F对导线做功W=FvΔ?t=F安vΔ?t=BILvΔ?t
电路获得的电能W电=qE=IEΔ?t=BILvΔ?t
可见,F对导线MN所做的功等于电路获得的电能W电;
导线MN中产生的焦耳热Q=I2RΔ?t=IΔ?t×IR=qE=W电
可见,电路获得的电能W电等于导线MN中产生的焦耳热Q。
23.解:(1)cd边刚进入磁场时,线框速度v=2g?
线框中产生的感应电动势:E=BLv=BL2g?
(2)此时线框中电流:I=ER?
cd两点间的电势差U=I(34R)=34E=34BL2g?
(3)安培力F=BIL=B2L22g?R
根据牛顿第二定律mg?F=ma,由a=0
解得下落高度满足:??=m2gR22B4L4
