数学人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共17张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 657.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 16:27:24 | ||
图片预览






文档简介
(共17张PPT)
1.2
空间向量基本定理
共线向量定理:
共面向量定理:
复习
对任意两个空间向量a,b(b≠0),a∥b的充要条件是
如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是
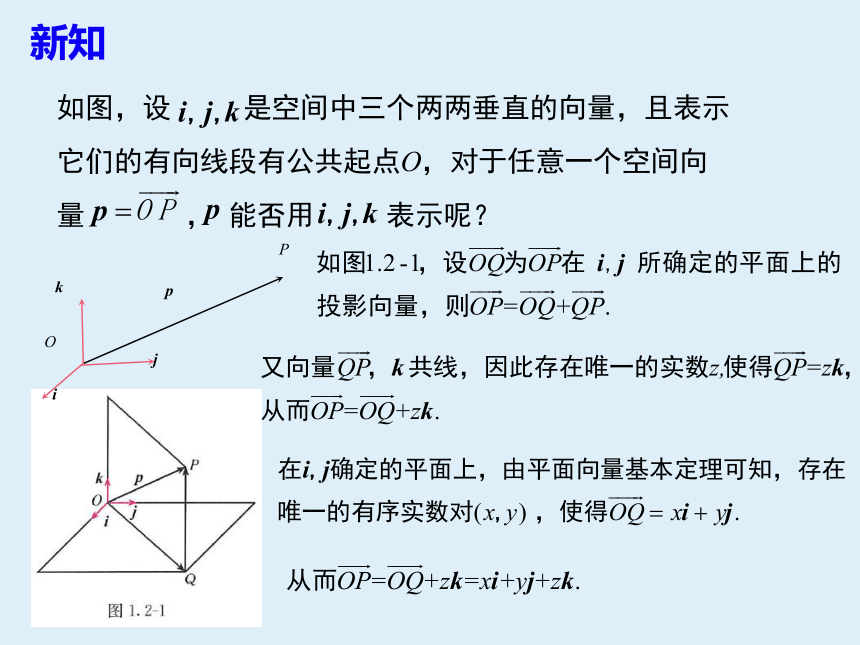
如图,设
是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点O,对于任意一个空间向量
,
能否用
表示呢?
O
i
j
p
P
k
新知
因此,如果
是空间三个两两垂直的向量,那么对于任意一个空间向量
,存在唯一的有序实组
,使得
.
我们称
分别为向量
在
上的分向量.
思考
你能证明唯一性吗?
证明:假设这种表示形式不唯一,即
还可以表示成
,那么
.
可得
.
由向量
不共面可以得到
探究
在空间中,如果用任意三个不共面的向量
代替两两垂直的向量
,你能得出类似的结论吗?
新知
空间向量基本定理
如果三个向量
不共面,那么对
任意一个空间向量
,存在唯一的有序实数组
,
使得
我们把
叫做空间的一个基底,
都叫做基向量.
所有空间向量组成的集合就是
新知
单位正交基底
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用
表示.
空间向量的正交分解
由空间向量基本定理可知,对空间中的任意向量
,均可以分解为三个向量
,使
,像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
(1)构成空间的基底是唯一的吗?
(2)基底选定后,空间中向量用基底表示,表示形式唯一吗?
(3)基向量可以为零向量吗?
思考
答案:不唯一
答案:唯一
答案:不可以.因为零向量与任意一个非零向量共线,与任意两个不共线的非零向量共面.
新知
练习
A
②
例1
如图1.2-2,
是四面体
的棱
的中点,点
在线段
上,点
在线段
上,且
用向量
表示
.
分析:
是三个不共面的向量,它们构成空间的一个基底
,
可以用基底
表示出来.
解:
例题
用基底表示向量(分解向量)的步骤:
定基底→找目标→下结论
练习
用基底表示向量(分解向量)的步骤:
定基底→找目标→下结论
例题
例题
在几何体中求空间向量的数量积、证明平行与垂直,求两条直线的夹角
①分解向量,转化为已知模和夹角的向量的数量积
②最后利用数量积的定义求解
归纳
练习
练习
练习
小结
1、空间向量基本定理
2、用基底表示向量的步骤:定基底、找目标、下结论
3、在几何体中求空间向量的数量积、证明平行与垂直,求两条直线的夹角
①分解向量,转化为已知模和夹角的向量的数量积
②利用数量积的定义求解
作业
课本P14练习2
1.2
空间向量基本定理
共线向量定理:
共面向量定理:
复习
对任意两个空间向量a,b(b≠0),a∥b的充要条件是
如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是
如图,设
是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点O,对于任意一个空间向量
,
能否用
表示呢?
O
i
j
p
P
k
新知
因此,如果
是空间三个两两垂直的向量,那么对于任意一个空间向量
,存在唯一的有序实组
,使得
.
我们称
分别为向量
在
上的分向量.
思考
你能证明唯一性吗?
证明:假设这种表示形式不唯一,即
还可以表示成
,那么
.
可得
.
由向量
不共面可以得到
探究
在空间中,如果用任意三个不共面的向量
代替两两垂直的向量
,你能得出类似的结论吗?
新知
空间向量基本定理
如果三个向量
不共面,那么对
任意一个空间向量
,存在唯一的有序实数组
,
使得
我们把
叫做空间的一个基底,
都叫做基向量.
所有空间向量组成的集合就是
新知
单位正交基底
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用
表示.
空间向量的正交分解
由空间向量基本定理可知,对空间中的任意向量
,均可以分解为三个向量
,使
,像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
(1)构成空间的基底是唯一的吗?
(2)基底选定后,空间中向量用基底表示,表示形式唯一吗?
(3)基向量可以为零向量吗?
思考
答案:不唯一
答案:唯一
答案:不可以.因为零向量与任意一个非零向量共线,与任意两个不共线的非零向量共面.
新知
练习
A
②
例1
如图1.2-2,
是四面体
的棱
的中点,点
在线段
上,点
在线段
上,且
用向量
表示
.
分析:
是三个不共面的向量,它们构成空间的一个基底
,
可以用基底
表示出来.
解:
例题
用基底表示向量(分解向量)的步骤:
定基底→找目标→下结论
练习
用基底表示向量(分解向量)的步骤:
定基底→找目标→下结论
例题
例题
在几何体中求空间向量的数量积、证明平行与垂直,求两条直线的夹角
①分解向量,转化为已知模和夹角的向量的数量积
②最后利用数量积的定义求解
归纳
练习
练习
练习
小结
1、空间向量基本定理
2、用基底表示向量的步骤:定基底、找目标、下结论
3、在几何体中求空间向量的数量积、证明平行与垂直,求两条直线的夹角
①分解向量,转化为已知模和夹角的向量的数量积
②利用数量积的定义求解
作业
课本P14练习2
