勾股定理
图片预览



文档简介
(共53张PPT)
人教版八年级(下)第十八章
这就是本届大会会徽的图案.
活动 1
你见过这个图案吗?
你听说过勾股定理吗?
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.
活动 2
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
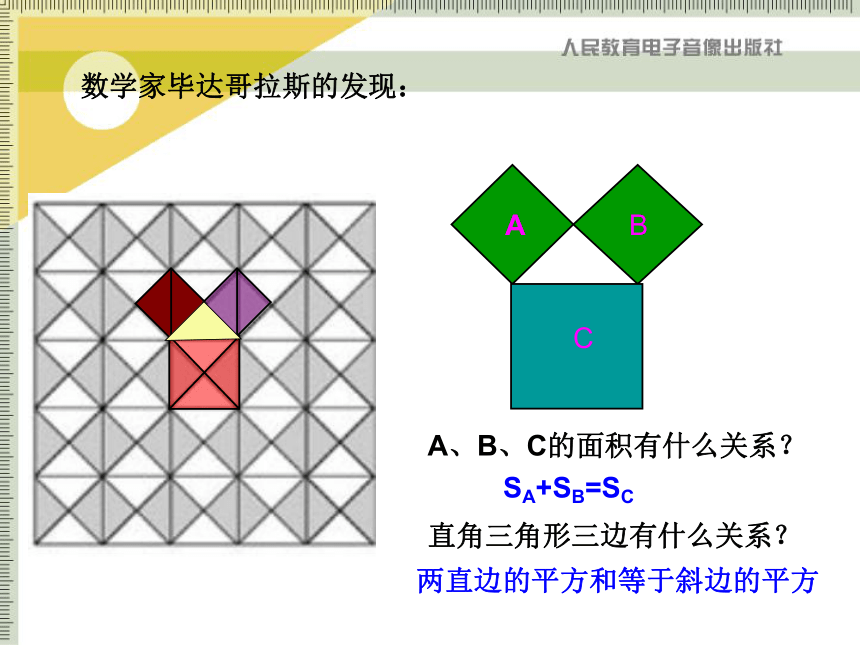
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
A
B
C
A
B
C
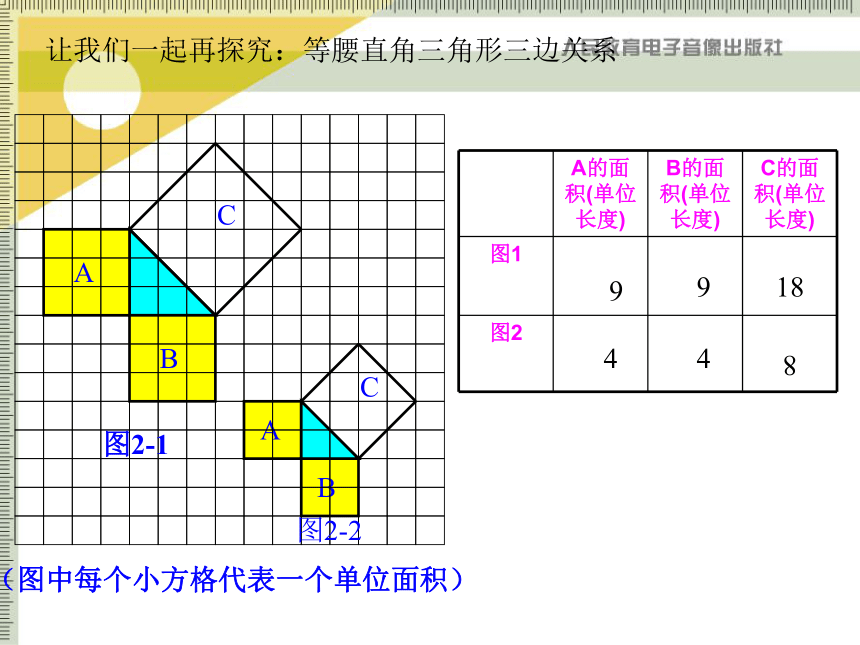
(图中每个小方格代表一个单位面积)
图2-1
图2-2
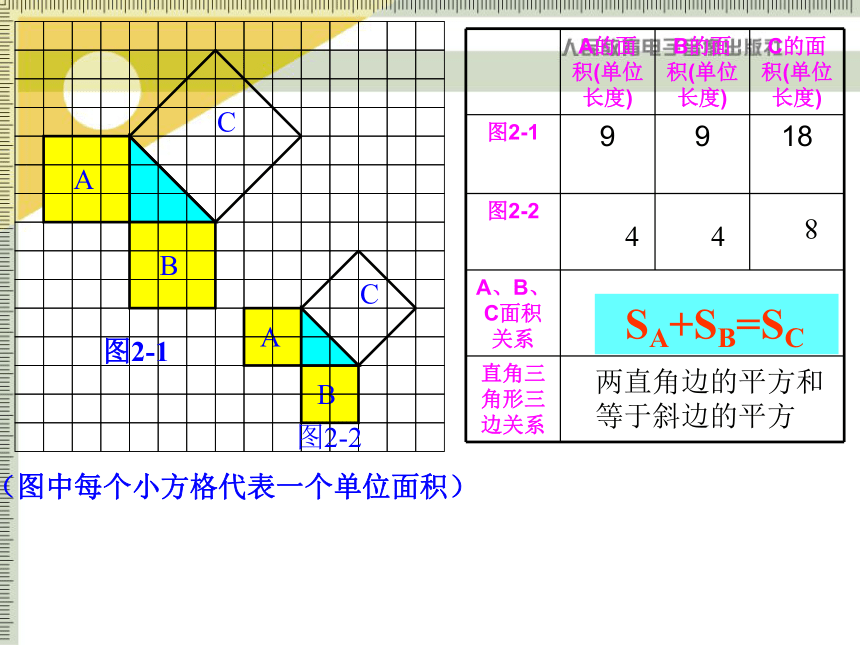
让我们一起再探究:等腰直角三角形三边关系
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图1
图2
9
9
18
4
4
8
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
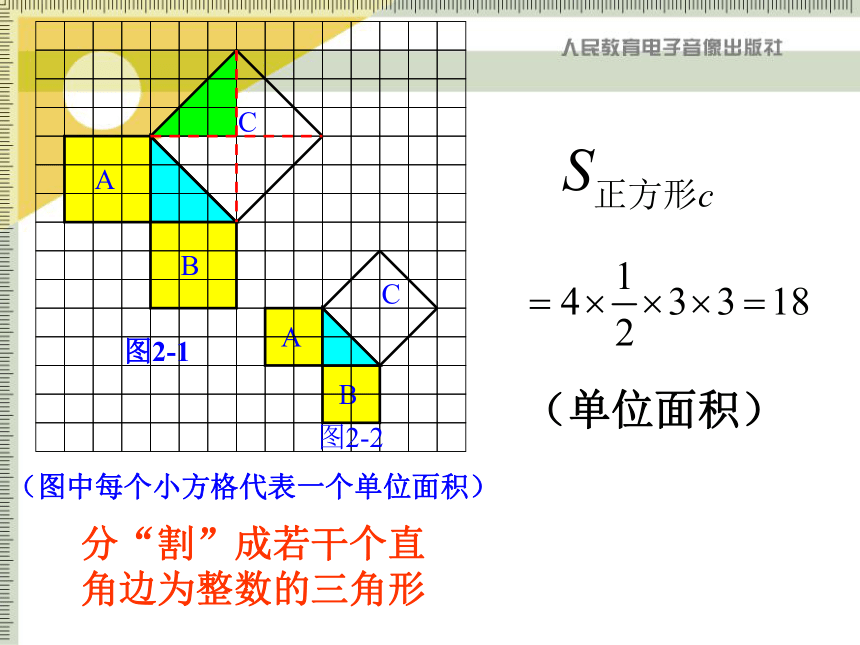
分“割”成若干个直角边为整数的三角形
(单位面积)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
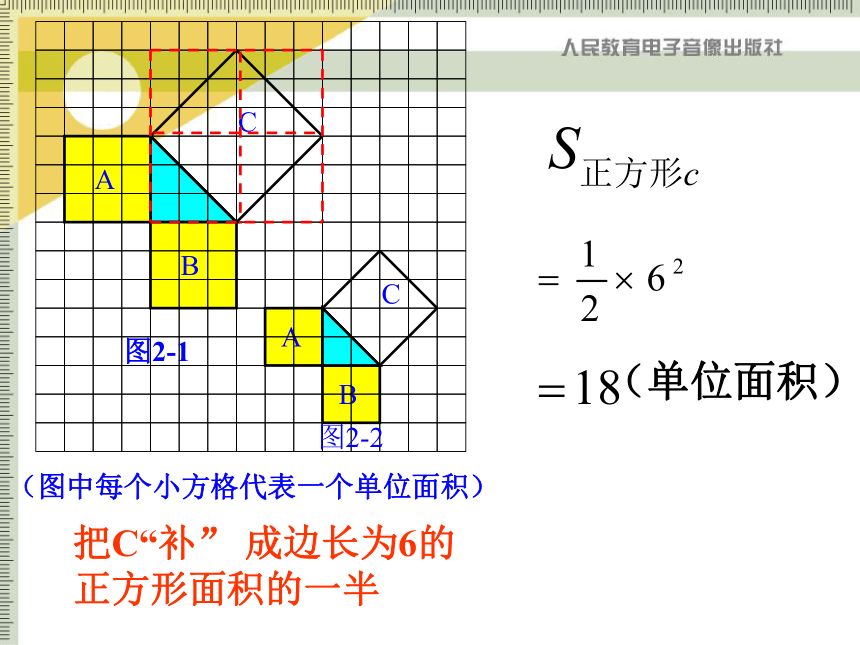
(单位面积)
把C“补” 成边长为6的正方形面积的一半
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
SA+SB=SC
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2-1 9 9 18
图2-2
A、B、C面积关系
直角三角形三边关系
4
4
8
两直角边的平方和
等于斜边的平方
A
B
C
图1-2
A
B
C
图1-3
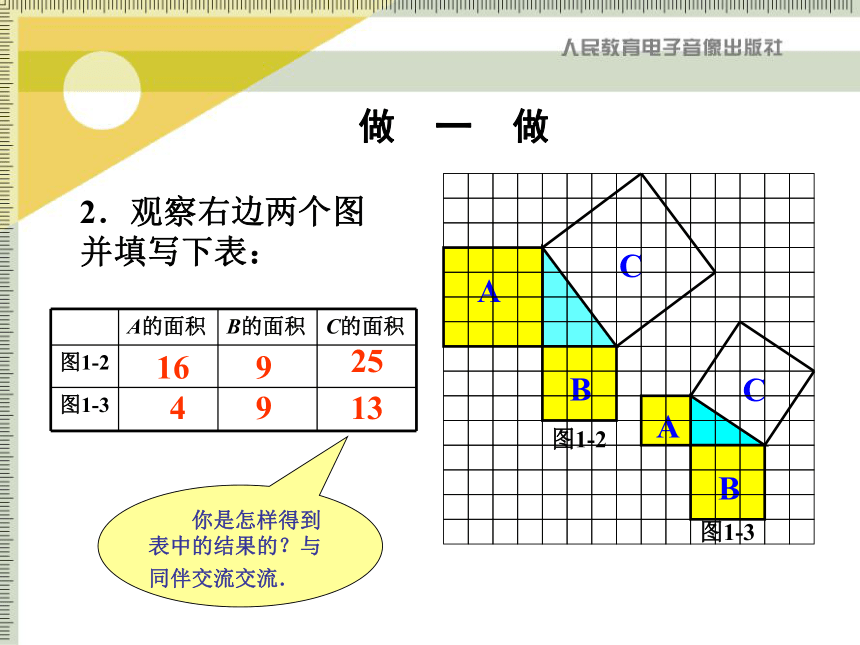
2.观察右边两个图并填写下表:
A的面积 B的面积 C的面积
图1-2
图1-3
16
9
25
4
9
13
你是怎样得到表中的结果的?与同伴交流交流.
做 一 做
A
B
C
图1-2
A
B
C
图1-3
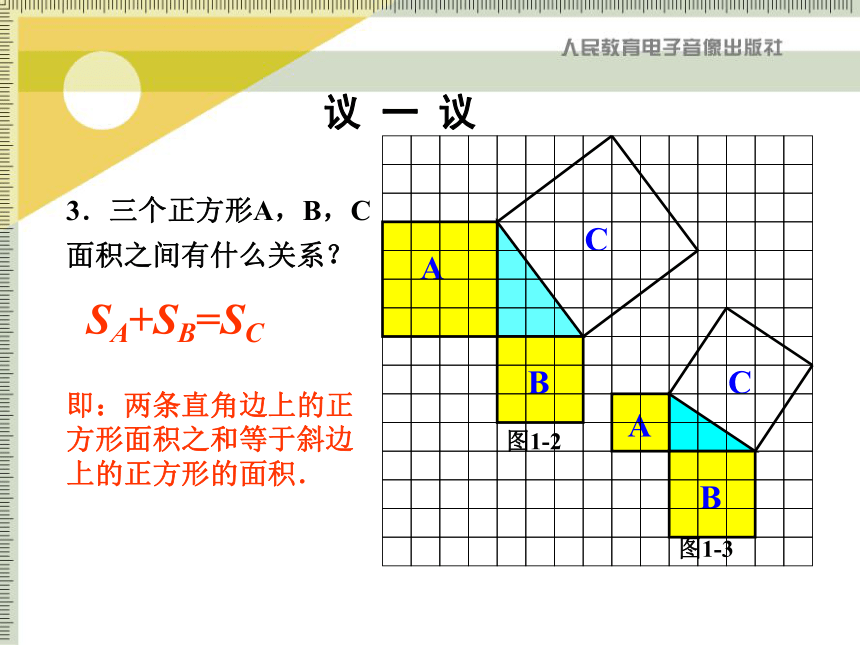
3.三个正方形A,B,C面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
议 一 议
A
B
C
a
c
b
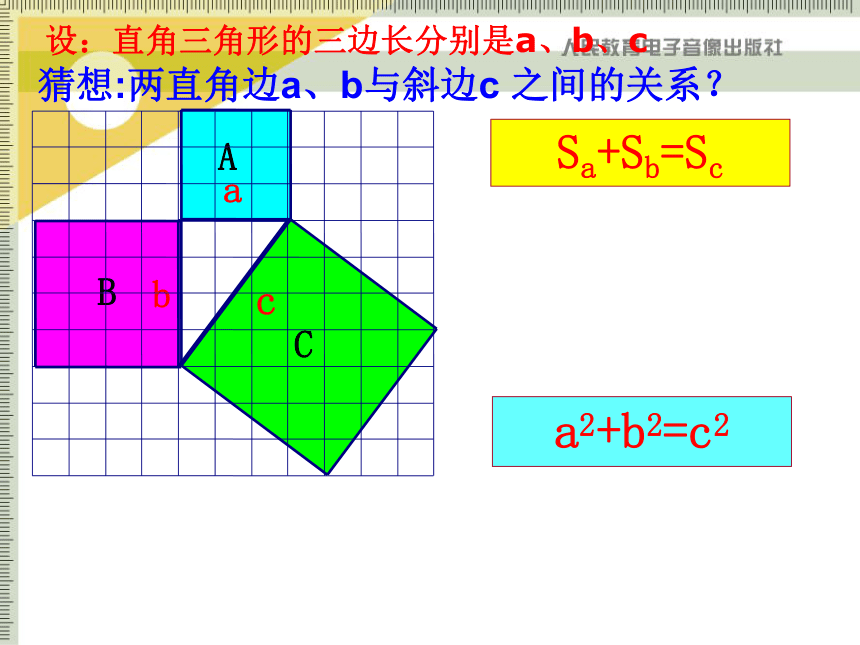
Sa+Sb=Sc
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
a2+b2=c2
a
c
b
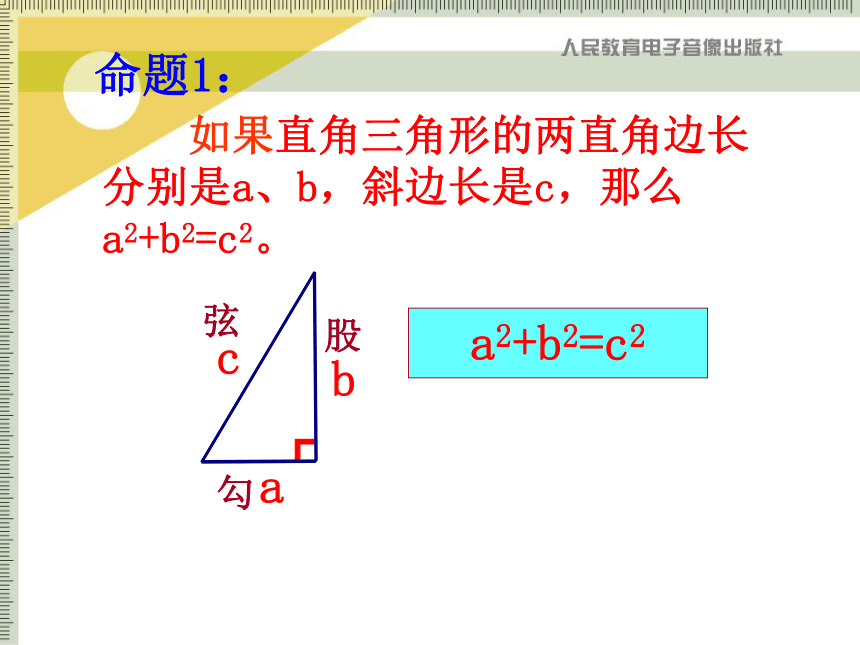
如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。
勾
股
弦
命题1:
活动 3
看左边的图案,这个图案是公元 3 世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
黄实
朱实
朱实
朱实
朱实
b
a
a
c
a
b
看一看
化简得: c2 =a2+ b2.
赵爽弦图的证法
c
b
a
(b-a)2
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
赵爽的“弦图”
早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”
思考:你能验证吗?
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
想一想:这四个直角三角形还能怎样拼?
证明一
b
a
b
a
b
a
b
a
c
c
c
c
大正方形的面积该怎样表示
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明二
a2
b2
a2 + b2 = c2
a2
b2
a2
c2
对比两个图形,你能直接观察验证出勾股定理吗?
a
证明六 印度婆什迦羅的證明
c
c2 = b2 + a2
b
证明八
证明八
证明八
证明八
证明八
a2
b2
证明九
证明九
证明九
证明九
证明九
c2
a2 + b2 = c2
证明九
证明九
拼图游戏
证明九
拼图游戏
无字证明
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
无字证明
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
证明十
I
II
III
注意:
面积 I :面积II :面积III = a2 : b2 : c2
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
由此得,面积 I + 面积 II = 面积 III
因此,a2 + b2 = c2 。
证明十
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
做一做:
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
小结:
活动 4
布置作业:
勾股定理从边的角度刻画了直角三角形的又一个特征.
人类对勾股定理的研究已有近3000年的历史,在西方,勾股定理又被称为“毕达哥拉斯定理”、“百牛定理”、“驴桥定理”等等 .
收集有关勾股定理的证明方法,下节课展示、交流.
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
人教版八年级(下)第十八章
这就是本届大会会徽的图案.
活动 1
你见过这个图案吗?
你听说过勾股定理吗?
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.
活动 2
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
让我们一起再探究:等腰直角三角形三边关系
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图1
图2
9
9
18
4
4
8
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
分“割”成若干个直角边为整数的三角形
(单位面积)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(单位面积)
把C“补” 成边长为6的正方形面积的一半
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
SA+SB=SC
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2-1 9 9 18
图2-2
A、B、C面积关系
直角三角形三边关系
4
4
8
两直角边的平方和
等于斜边的平方
A
B
C
图1-2
A
B
C
图1-3
2.观察右边两个图并填写下表:
A的面积 B的面积 C的面积
图1-2
图1-3
16
9
25
4
9
13
你是怎样得到表中的结果的?与同伴交流交流.
做 一 做
A
B
C
图1-2
A
B
C
图1-3
3.三个正方形A,B,C面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
议 一 议
A
B
C
a
c
b
Sa+Sb=Sc
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
a2+b2=c2
a
c
b
如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。
勾
股
弦
命题1:
活动 3
看左边的图案,这个图案是公元 3 世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
黄实
朱实
朱实
朱实
朱实
b
a
a
c
a
b
看一看
化简得: c2 =a2+ b2.
赵爽弦图的证法
c
b
a
(b-a)2
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
赵爽的“弦图”
早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”
思考:你能验证吗?
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
想一想:这四个直角三角形还能怎样拼?
证明一
b
a
b
a
b
a
b
a
c
c
c
c
大正方形的面积该怎样表示
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明二
a2
b2
a2 + b2 = c2
a2
b2
a2
c2
对比两个图形,你能直接观察验证出勾股定理吗?
a
证明六 印度婆什迦羅的證明
c
c2 = b2 + a2
b
证明八
证明八
证明八
证明八
证明八
a2
b2
证明九
证明九
证明九
证明九
证明九
c2
a2 + b2 = c2
证明九
证明九
拼图游戏
证明九
拼图游戏
无字证明
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
无字证明
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
证明十
I
II
III
注意:
面积 I :面积II :面积III = a2 : b2 : c2
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
由此得,面积 I + 面积 II = 面积 III
因此,a2 + b2 = c2 。
证明十
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
做一做:
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
小结:
活动 4
布置作业:
勾股定理从边的角度刻画了直角三角形的又一个特征.
人类对勾股定理的研究已有近3000年的历史,在西方,勾股定理又被称为“毕达哥拉斯定理”、“百牛定理”、“驴桥定理”等等 .
收集有关勾股定理的证明方法,下节课展示、交流.
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
