23.2.1中心对称说课
图片预览










文档简介
(共44张PPT)
数学人教版九年级上册
23.2.1
2012.03.15
教材分析
学情分析
教学过程
设计理念
教法学法分析
本节课是在学生学移、轴对称、旋转三种几何变换之后由旋转变换引入的。它为前面所学的几何图形(平行四边形)的性质做了归纳与提升,同时也为后面学习的中心对称图形和第24章《圆》的学习做好知识准备,也使得初中阶段的学生在几何变换方面的知识结构趋于完整。
地位和作用
学习目标
知识与能力目标:
1、了解中心对称的有关概念;
2、理解中心对称的性质;
3、会运用中心对称的性质作图。
过程与方法目标:
1、通过对中心对称的性质的探究及运用,初步学会从正反两方面去思考问题的数学思考方法.以及类比思想的应用;
2、能用中心对称的性质准确作出已知图形关于某点中心对称的图形;
情感目标:
培养严谨的科学态度和探索精神,经历数学知识融于生活实际的学习过程,体验数学学习的快乐。
重点
中心对称的定义、性质及应用
难点
中心对称性质的应用
本节课是在学生学习了旋转的基础上引入的,学生在学习旋转的过程中,已经充分体验了观察、测量、旋转画图等活动,经历了在操作活动中探索性质的过程,获得了初步的数学活动经验和体验,具备了一定的主动参与、合作交流的意识和初步的观察、分析、抽象概括能力,但是学生在解决问题时往往依赖于生活经历等具体、直观的形象,通过本节课的学习将进一步提高观察、思考、分析、归纳、探索、创新等能力。
针对本节课的特点,我采用我校的“四段七环”教学法。由于学生已经初步具备了观察、分析、归纳、逻辑推理能力,所以我让学生采用动手实践、自主探究、合作交流的学习方法。在教师的组织引导下,通过多媒体的配合教学,让学生体验一个充满着观察、实验、类比与归纳的探索过程,让学生自主探究新知,真正成为学习的主人,使数学课成为学生构建自己知识体系的场所。同时给学生提供展示机会,培养学生的交流能力及学习数学的自信心。
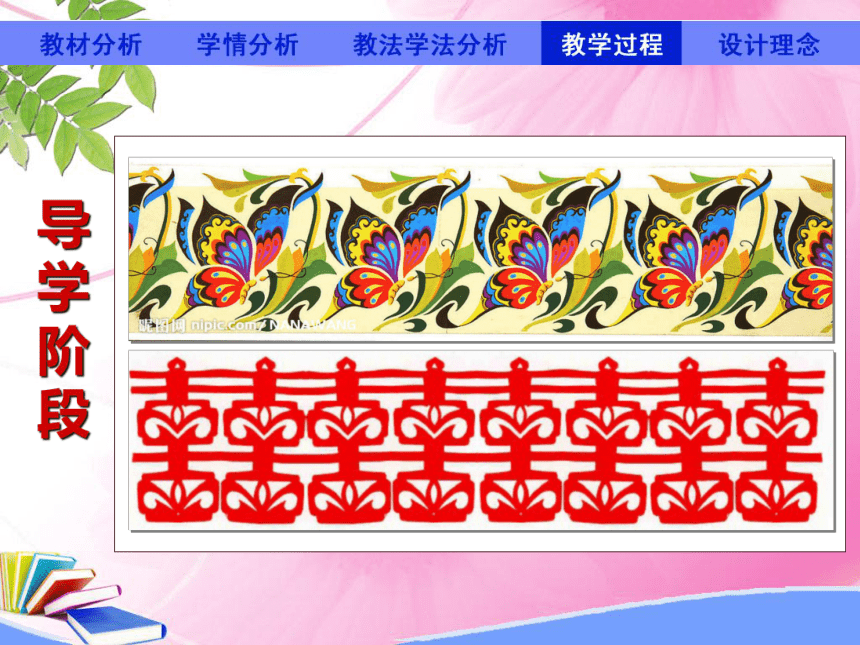
导学阶段
导学阶段
导学阶段
导学阶段
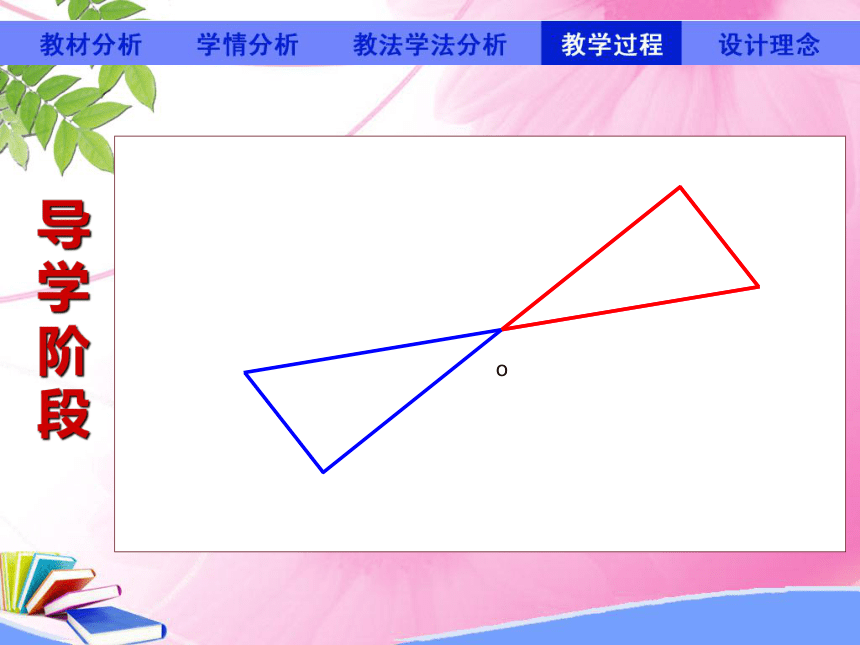
o
导学阶段
学习目标
1、了解中心对称的有关概念
2、理解中心对称的性质
3、会运用中心对称的性质作图
4、通过对中心对称的性质的探究及运用,初步学会从正反两方面去思考问题的数学思考方法,以及类比思想的应用
5、能用中心对称的性质准确作出已知图形关于某点中心对称的图形
导学阶段
活动一:自学课本第62页内容。
要点:1、什么是中心对称?
2、什么是对称中心、对称点?
3、对称中心在图形中的位置如何?
(图形上、图形外)
4、疑惑问题小组讨论。
探究解疑阶段
活动二:动手做一做
利用手中的三角板在平面内画一个与三角板成中心对称的三角形。思考:内框构成的两个三角形是不是中心对称的?连接每对对称点,你会发现什么?小组内交流一下。
探究解疑阶段
设计意图:活动1根据内容特点由学生自学,充分发挥学生的主观能动性,加深对概念的理解。从中也培养学生阅读、理解、概括能力,养成良好的自学习惯。活动2通过学生的动手操作,培养了学生的动手能力、观察能力和探究问题的能力,同时也为强化重点、突破难点做好铺垫。本阶段主要以小组合作的形式来完成,充分体现了学生的主体地位,也提高了学生合作交流的能力。
探究解疑阶段
反馈矫正 归纳总结
1、检查自学效果
反馈矫正 归纳总结
点O是AA′的中点。
O
●
△ABC≌△A′B′C′
A′
C′
B′
C
A
B
1、中心对称的两个图形,对称点所连线段 经过对称中心,而且被对称中心所平分。
2、中心对称的两个图形是全等形。
反馈矫正 归纳总结
A
O
A′
(1)以点O为对称中心,作出点A的对称点A′
点A′即为所求的点
2、想一想,做一做
反馈矫正 归纳总结
A
A′
B′
B
O
(2)以点O为对称中心,作出线段AB的对称线段A′B′。
反馈矫正 归纳总结
(3)选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
A′
C′
B′
△A′B′C′即为所求的三角形。
反馈矫正 归纳总结
设计意图
检查自学效果充分调动了学生的积极性,也给了学生展示的机会,很大程度上培养了学生的学习兴趣。动手操作活动由简单到复杂、由部分到整体,符合学生的认知规律,也让学生感到学有所用。同时把难点问题层层分解利于突破难点。
反馈矫正 归纳总结
3、变式练习
练习一 画一个与已知四边形ABCD中心对称的图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。
(3)以四边形内部一点为对称中心。
反馈矫正 归纳总结
练习二 如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
解法二:
解法一:
反馈矫正 归纳总结
设计意图:练习一让学生感受随着对称中心位置的变化,图形位置关系在变化,这对学生的应用能力是一大提升。练习二让学生由中心对称的性质出发,去寻求对称中心的位置,培养了学生的逆向思维和发散思维。通过让学生动手操作,巩固了中心对称的性质及基本作图方法,这样的安排既强化了本节课的重点,也突破了难点。在小组中展开讨论,让学生有相互学习的机会。
反馈矫正 归纳总结
反馈矫正 归纳总结
4、归纳
(1)各小组在组长的带领之下谈本节课的收获,提出自己的疑惑,然后教师抽查。
轴对称 中心对称
定义三要素 1 有一条对称轴 有一个对称中心
2 翻折180度 旋转180度
3 前后图形重合 前后图形重合
性质 1 前后图形全等 前后图形全等
2 对称轴垂直平分对称点连线 对称中心平分对称点连线
反馈矫正 归纳总结
(2)填表
设计意图:通过本节课的创境导入、探究解疑、反馈矫正等环节的教学,引导学生归纳总结轴对称和中心对称的异同点,使得学生建立了完整的知识体系也使得本节课的知识得到升华。各小组在组长带领之下总结本节课的要点,提高发言率,真正成为高效课堂。
反馈矫正 归纳总结
1、达标检测:画出与△ABC关于点O对称的△A′B′C′ 。
应用评价阶段
2、分层布置作业:
必做题(习题1)
选做题(思考:两个全等形一定中
心对称吗?)
应用评价阶段
设计意图:必做题引导学生复习、巩固本节课的知识,学会总结反思,为今后学习打下基础。选做题启发学生进一步思考两个图形中心对称的条件,更深层次的加深了对中心对称的理解。作业布置体现以人为本。
应用评价阶段
板书设计:
标 题
定义
性质 教师作图 学生演示
时间安排
导学阶段:3分钟
探究解疑阶段:12分钟
反馈矫正:13分钟
归纳总结阶段:5分钟
应用评价阶段:7分钟
新课标指出:数学教育要面向全体学生,适应学生个性发展的需要,使得:人人都能获得良好的数学教育,不同的人在数学上得到不同的发展。在教学中我给了学生充分发挥的舞台,根据学生的年龄特征、个性特征设计活动,让学生各方面的能力都得到了充分的发展,也感受到了学习数学的乐趣。
备用
像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
例1(3) 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。
A
B
A’
C’
B’
D’
D
O
C
四边形A1B1C1D1即为所求的图形。
导学阶段
数学人教版九年级上册
23.2.1
2012.03.15
教材分析
学情分析
教学过程
设计理念
教法学法分析
本节课是在学生学移、轴对称、旋转三种几何变换之后由旋转变换引入的。它为前面所学的几何图形(平行四边形)的性质做了归纳与提升,同时也为后面学习的中心对称图形和第24章《圆》的学习做好知识准备,也使得初中阶段的学生在几何变换方面的知识结构趋于完整。
地位和作用
学习目标
知识与能力目标:
1、了解中心对称的有关概念;
2、理解中心对称的性质;
3、会运用中心对称的性质作图。
过程与方法目标:
1、通过对中心对称的性质的探究及运用,初步学会从正反两方面去思考问题的数学思考方法.以及类比思想的应用;
2、能用中心对称的性质准确作出已知图形关于某点中心对称的图形;
情感目标:
培养严谨的科学态度和探索精神,经历数学知识融于生活实际的学习过程,体验数学学习的快乐。
重点
中心对称的定义、性质及应用
难点
中心对称性质的应用
本节课是在学生学习了旋转的基础上引入的,学生在学习旋转的过程中,已经充分体验了观察、测量、旋转画图等活动,经历了在操作活动中探索性质的过程,获得了初步的数学活动经验和体验,具备了一定的主动参与、合作交流的意识和初步的观察、分析、抽象概括能力,但是学生在解决问题时往往依赖于生活经历等具体、直观的形象,通过本节课的学习将进一步提高观察、思考、分析、归纳、探索、创新等能力。
针对本节课的特点,我采用我校的“四段七环”教学法。由于学生已经初步具备了观察、分析、归纳、逻辑推理能力,所以我让学生采用动手实践、自主探究、合作交流的学习方法。在教师的组织引导下,通过多媒体的配合教学,让学生体验一个充满着观察、实验、类比与归纳的探索过程,让学生自主探究新知,真正成为学习的主人,使数学课成为学生构建自己知识体系的场所。同时给学生提供展示机会,培养学生的交流能力及学习数学的自信心。
导学阶段
导学阶段
导学阶段
导学阶段
o
导学阶段
学习目标
1、了解中心对称的有关概念
2、理解中心对称的性质
3、会运用中心对称的性质作图
4、通过对中心对称的性质的探究及运用,初步学会从正反两方面去思考问题的数学思考方法,以及类比思想的应用
5、能用中心对称的性质准确作出已知图形关于某点中心对称的图形
导学阶段
活动一:自学课本第62页内容。
要点:1、什么是中心对称?
2、什么是对称中心、对称点?
3、对称中心在图形中的位置如何?
(图形上、图形外)
4、疑惑问题小组讨论。
探究解疑阶段
活动二:动手做一做
利用手中的三角板在平面内画一个与三角板成中心对称的三角形。思考:内框构成的两个三角形是不是中心对称的?连接每对对称点,你会发现什么?小组内交流一下。
探究解疑阶段
设计意图:活动1根据内容特点由学生自学,充分发挥学生的主观能动性,加深对概念的理解。从中也培养学生阅读、理解、概括能力,养成良好的自学习惯。活动2通过学生的动手操作,培养了学生的动手能力、观察能力和探究问题的能力,同时也为强化重点、突破难点做好铺垫。本阶段主要以小组合作的形式来完成,充分体现了学生的主体地位,也提高了学生合作交流的能力。
探究解疑阶段
反馈矫正 归纳总结
1、检查自学效果
反馈矫正 归纳总结
点O是AA′的中点。
O
●
△ABC≌△A′B′C′
A′
C′
B′
C
A
B
1、中心对称的两个图形,对称点所连线段 经过对称中心,而且被对称中心所平分。
2、中心对称的两个图形是全等形。
反馈矫正 归纳总结
A
O
A′
(1)以点O为对称中心,作出点A的对称点A′
点A′即为所求的点
2、想一想,做一做
反馈矫正 归纳总结
A
A′
B′
B
O
(2)以点O为对称中心,作出线段AB的对称线段A′B′。
反馈矫正 归纳总结
(3)选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
A′
C′
B′
△A′B′C′即为所求的三角形。
反馈矫正 归纳总结
设计意图
检查自学效果充分调动了学生的积极性,也给了学生展示的机会,很大程度上培养了学生的学习兴趣。动手操作活动由简单到复杂、由部分到整体,符合学生的认知规律,也让学生感到学有所用。同时把难点问题层层分解利于突破难点。
反馈矫正 归纳总结
3、变式练习
练习一 画一个与已知四边形ABCD中心对称的图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。
(3)以四边形内部一点为对称中心。
反馈矫正 归纳总结
练习二 如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
解法二:
解法一:
反馈矫正 归纳总结
设计意图:练习一让学生感受随着对称中心位置的变化,图形位置关系在变化,这对学生的应用能力是一大提升。练习二让学生由中心对称的性质出发,去寻求对称中心的位置,培养了学生的逆向思维和发散思维。通过让学生动手操作,巩固了中心对称的性质及基本作图方法,这样的安排既强化了本节课的重点,也突破了难点。在小组中展开讨论,让学生有相互学习的机会。
反馈矫正 归纳总结
反馈矫正 归纳总结
4、归纳
(1)各小组在组长的带领之下谈本节课的收获,提出自己的疑惑,然后教师抽查。
轴对称 中心对称
定义三要素 1 有一条对称轴 有一个对称中心
2 翻折180度 旋转180度
3 前后图形重合 前后图形重合
性质 1 前后图形全等 前后图形全等
2 对称轴垂直平分对称点连线 对称中心平分对称点连线
反馈矫正 归纳总结
(2)填表
设计意图:通过本节课的创境导入、探究解疑、反馈矫正等环节的教学,引导学生归纳总结轴对称和中心对称的异同点,使得学生建立了完整的知识体系也使得本节课的知识得到升华。各小组在组长带领之下总结本节课的要点,提高发言率,真正成为高效课堂。
反馈矫正 归纳总结
1、达标检测:画出与△ABC关于点O对称的△A′B′C′ 。
应用评价阶段
2、分层布置作业:
必做题(习题1)
选做题(思考:两个全等形一定中
心对称吗?)
应用评价阶段
设计意图:必做题引导学生复习、巩固本节课的知识,学会总结反思,为今后学习打下基础。选做题启发学生进一步思考两个图形中心对称的条件,更深层次的加深了对中心对称的理解。作业布置体现以人为本。
应用评价阶段
板书设计:
标 题
定义
性质 教师作图 学生演示
时间安排
导学阶段:3分钟
探究解疑阶段:12分钟
反馈矫正:13分钟
归纳总结阶段:5分钟
应用评价阶段:7分钟
新课标指出:数学教育要面向全体学生,适应学生个性发展的需要,使得:人人都能获得良好的数学教育,不同的人在数学上得到不同的发展。在教学中我给了学生充分发挥的舞台,根据学生的年龄特征、个性特征设计活动,让学生各方面的能力都得到了充分的发展,也感受到了学习数学的乐趣。
备用
像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
例1(3) 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。
A
B
A’
C’
B’
D’
D
O
C
四边形A1B1C1D1即为所求的图形。
导学阶段
同课章节目录
