19.1.1_平行四边形的性质(1)
文档属性
| 名称 | 19.1.1_平行四边形的性质(1) |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-09 22:24:45 | ||
图片预览




文档简介
(共52张PPT)
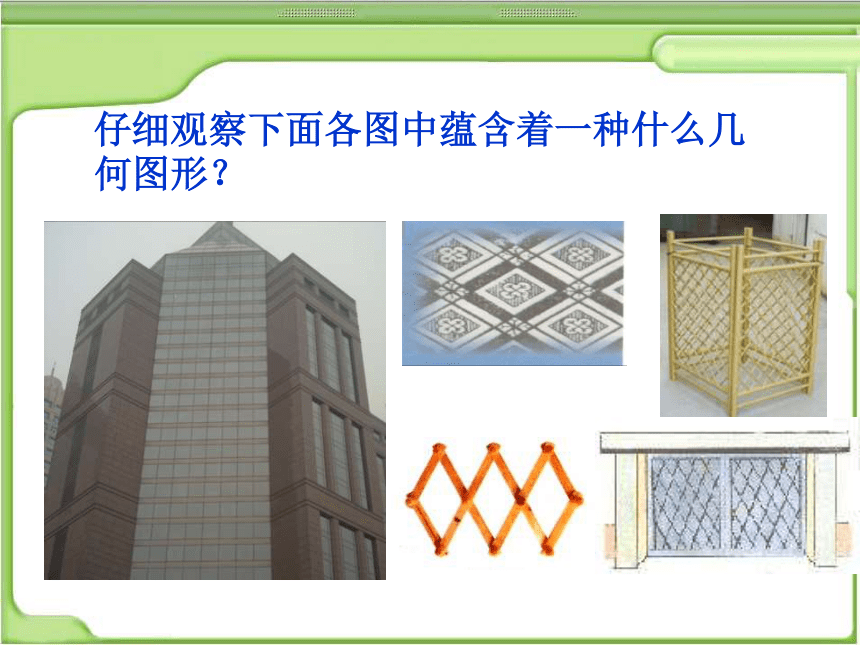
仔细观察下面各图中蕴含着一种什么几何图形?
活动
你能用手中一对全等的三角形纸片拼出几个平行四边形?
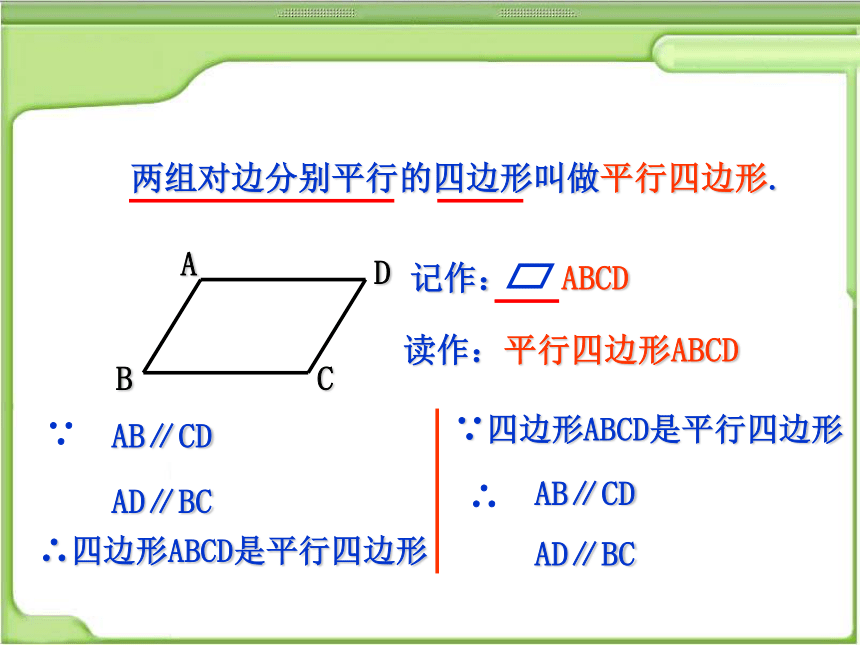
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
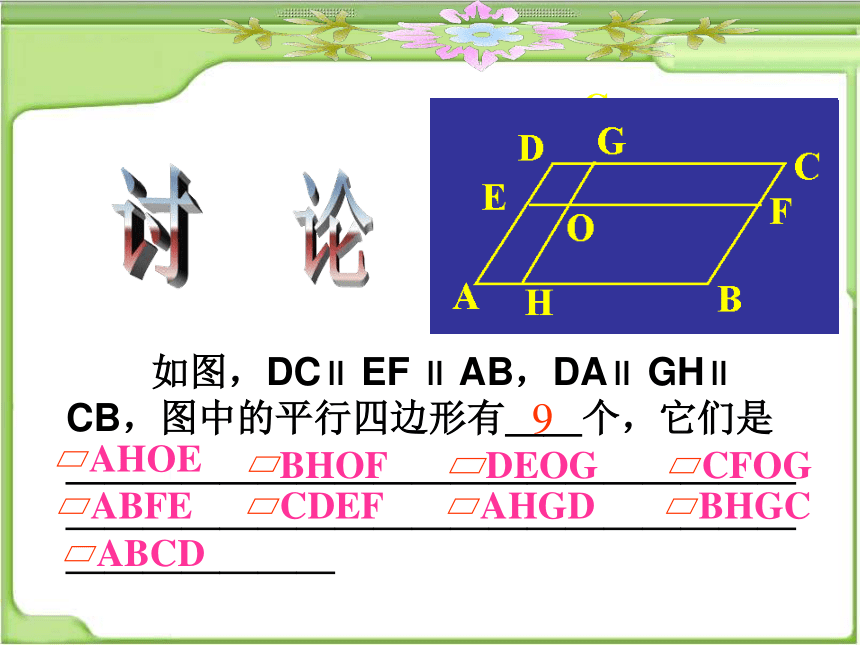
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_____________________________________________
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
D
A
B
C
O
H
E
F
G
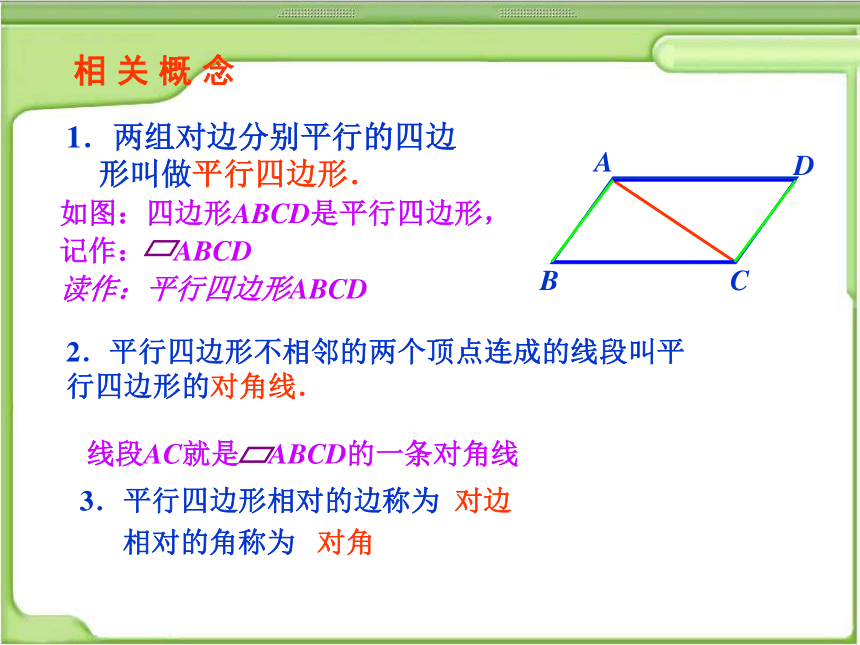
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形,
记作: ABCD
读作:平行四边形ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边
相对的角称为 对角
相 关 概 念
A
D
C
B
线段AC就是 ABCD的一条对角线
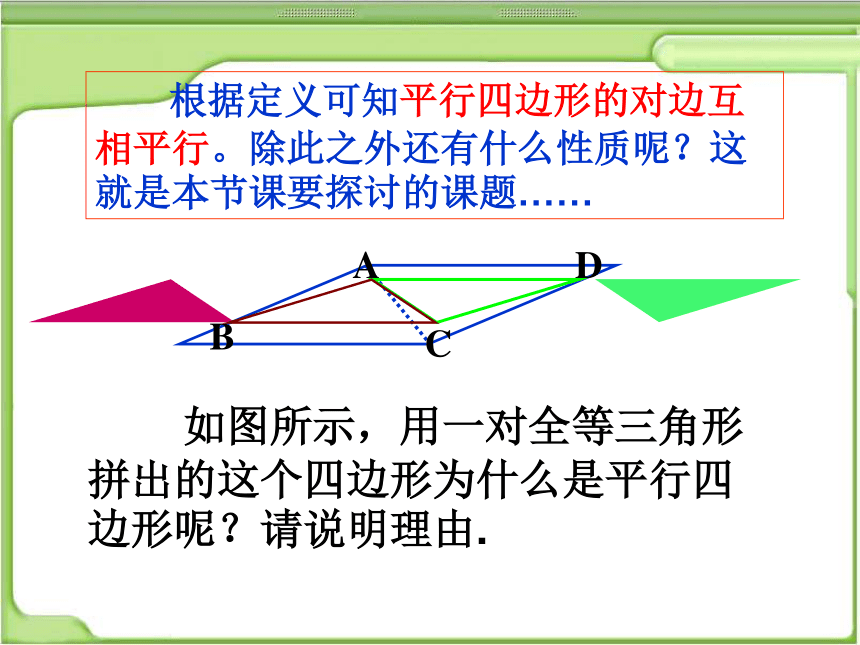
如图所示,用一对全等三角形拼出的这个四边形为什么是平行四边形呢?请说明理由.
A
B
C
D
根据定义可知平行四边形的对边互相平行。除此之外还有什么性质呢?这就是本节课要探讨的课题……
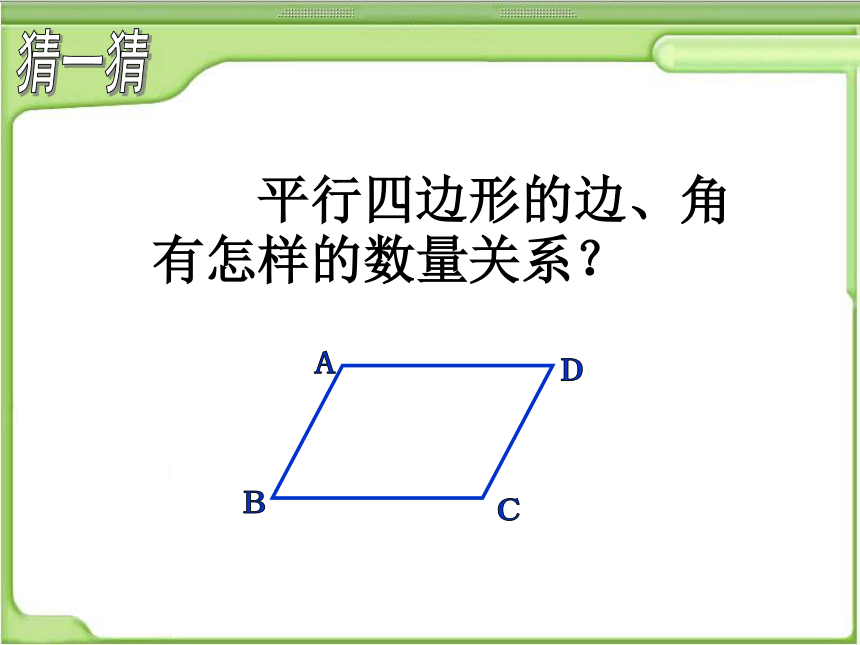
平行四边形的边、角有怎样的数量关系?
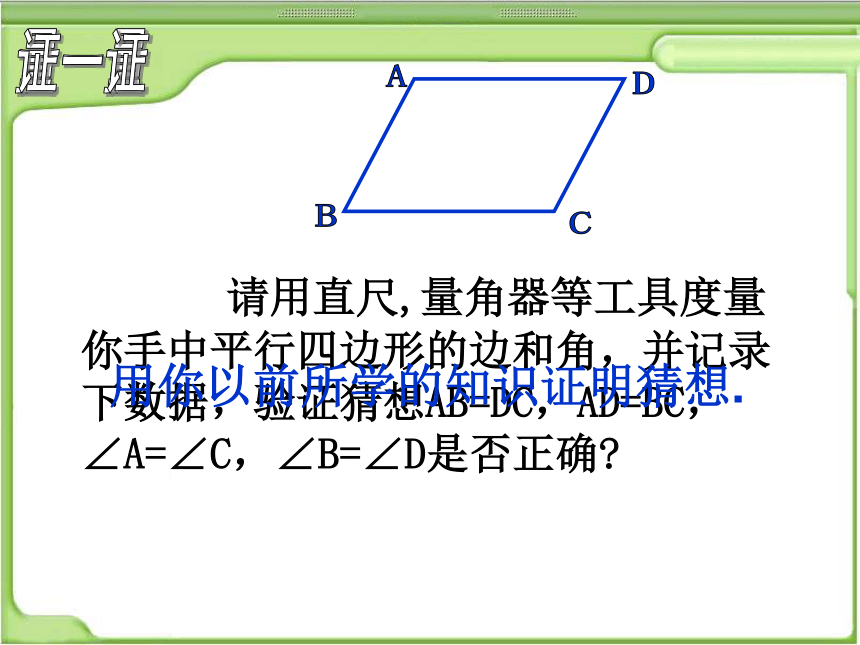
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
用你以前所学的知识证明猜想.
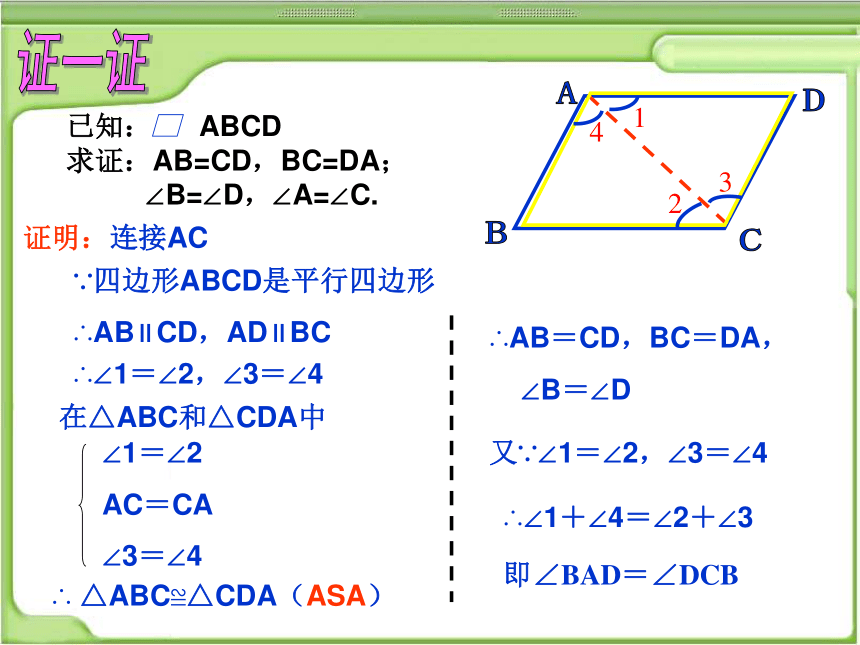
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
几何语言:
定理1:平行四边形的对边相等
定理2:平行四边形的对角相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C,∠B=∠D.(平行四边形的对角相等)
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C,∠B=∠D.(平行四边形的对角相等)
A
B
C
D
如果已知平行四边形一个内角的度数,能确定其他三个内角的度数吗?说说你的理由。
通常四边形问题要转化为三角形问题.
平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的邻角互补.
平行四边形的性质
A
B
C
D
1
2
3
4
用符号语言表示:如图
A
B
C
D
ABCD
AD∥ BC, AB∥ DC
AD=BC, AB=DC
∠ A=∠ C, ∠ B=∠ D
小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。
1、在 ABCD中,已知∠A=130°,
则∠B=__ ,∠C=___ ,∠D=___.
2、在 ABCD中,AB=2,BC=3,
则这个平行四边形的周长是______.
课堂练习
50°
50°
130°
10
例1:如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
解:∵四边形ABCD是平行四边形,
∴∠A=∠C, ∠A+∠B=180°.
∵∠A+∠C=200°,
∴∠A=100°,∠B=80°.
⑴ 其他三条边各长多少?
随堂练习
1.在 ABCD中, AB=3cm,BC=8cm,则 ABCD的周长
是 cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3. ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
4.如图,在 ABCD中,∠B的平分线BE交AD于E,BC=5,
AB=3,则ED的长为 .
(第3题)
22
10cm,5cm
2
10
10
课堂小结
通过本节课的学习,你有哪些收获?
1.平行四边形的概念
两组对边分别平行的四边形叫做平行四边形
2.平行四边形的性质
平行四边形的对边平行且相等
平行四边形的对角相等
平行四边形的邻角互补。
3.解决平行四边形的有关问题经常连接对角线将
之转化为三角形的问题。
随堂练习1
如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝;
BC= ㎝;AD= ㎝。
2)若∠A=70°,则∠B= , ∠C= ; ∠D= 。
3)若∠A+∠C=80°,
则∠A= ; ∠D= 。
6
9
9
110°
70°
110°
40°
140°
1.已知: ABCD中,∠A=100°,你能求出其他各角的度数吗?说说你的理由.
∠B=80°
∠C=100°
∠ D=80°
A
D
C
B
随堂练习2
2.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
28
32
3cm
A
B
D
C
5cm
4cm
3.求如图所示的四边形ABCD的面积.
3cm
A
B
D
C
E
9cm
5cm
4.如图所示,若BE平分∠ABC,
则ED= .
4cm
2
3
5cm
5cm
4cm
1
比较线路长短
如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.
9
A
B
C
D
E
G
F
H
O
从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由.
上图的平行四边形ABCD中有几对全等三角形 有几对相等的线段
D
C
B
A
O
O
议一议
证明:
∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BAC
∴∠BAD=∠CAD
∵AB//EF ∴ ∠BAD=∠AEF
∴∠CAD =∠AEF ∴ AF=EF
∴ AF=BM
如图, 在 ABC中, AD平分∠BAC, 点M,E,F分别是AB,AD,AC上的点, 四边形BEFM是平行四边形. 求证:AF=BM
B
D
C
E
F
A
M
1.如图,四边形ABCD是平行四边形,填空
(1) ∠ADC=__,∠BCD=__
(2) ABCD的周长=____
B
A
D
C
30
20
50°
50°
130°
100
A
B
D
C
F
E
2.已知 ABCD,延长AB到E, 延长CD到F ,使BE=DF
求证: AF=CE
想一想做一做
A
B
D
C
F
E
2.已知 ABCD,延长AB到E, 延长CD到F ,使BE=DF, 求证: AF=CE
想一想做一做
1
2
3
4
∴ ADE≌ CBF(SAS)
解:∵ ABCD是平行四边形
∴AD=BC, ∠1=∠2
∵∠1+∠3=1800
∠2+∠4=1800
∴ ∠3= ∠4
∵ DF=BE
∴AF=CE
检测考试题
(1).在平行四边形ABCD中, ∠B=110°,延长AD至F,延长CD至E,连结EF, 求∠ E+∠ F.
(2). 在 ABCD中,连结BD, E,F是BD上的两点,且DE=BF, 求证: AE=CF.
D
F
A
B
C
E
E
F
∴ ∠B= ∠ADC=110°
∴ ∠EDF=110°
解:∵ ABCD是平行四边形
∵ ∠ADC=∠EDF
∴ ∠ E+ ∠F= 70°
(2). 在 ABCD中,连结BD, E,F是BD上的两点,且DE=BF, 求证: AE=CF.
E
F
∴ ADE≌ CBF
解:∵ ABCD是平行四边形
∴AD=BC
∵AD∥BC
∴ ∠ADE= ∠CBF
∵ DE=BF
∴AE=CF
检测考试题
(3).在 ABCD中,AE既是中线,又是高线,
如果 ABCD的周长为20cm, ABC的周长
比 ABCD的周长少6cm,
求 ABCD各边的长.
E
解: ∵ ABCD的周长为20cm ∴AB+BC=10cm
∵ ABC的周长比 ABCD的周长少6cm
∴AC= 4cm
∵ AE既是中线,又是高线
∴ AE 垂直平分BC, ∴AB= AC=4cm
∴CD=4cm BC=6cm AD=6cm
检测考试题
有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,
你能根据测得的数据计算
出DE的长度和∠D的度数吗?
AE∥BC
AB∥CF
四边形ABCD是平行四边形
∠B=60°
∠B=∠D
AD=BC=80
∠D=60°
DE=AD-AE
AE=60
DE=20cm
解:
课本P90, [习题19.1]
第1、2、6题。
预习课本P85~86的内容 。
课后作业
首页
上页
下页
知识与技能:
1、平行四边形的定义:两组对边分别
平行的四边形叫做平行四边形.
2、平行四边形的性质: 平行四边形的
对边平行且相等;平行四边形的对
角相等.
数学思想与方法:
1、“猜想——验证——证明”的科
学研究方法.
2、转化的数学思想.
感悟与收获
如图,在 ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长度?
F
D
C
B
A
E
活动与探究
首页
上页
下页
已知如图:E、F是平行四边形ABCD的对角线AC上的两点,AE=CF
求证:(1)△ADF≌ △CBE
(2)EB∥DF
1
2
3
4
已知:如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,BE平分∠ABC交AD于E,交CD的延长线于F.
⑴△ABE与△DFE全等吗?
A
B
C
D
E
F
⑵求CF的长.
⑶若连结CE,则CE与BE有怎样的位置关系?
⑷能否求出CE的长?
任画一个三角形,你能通过平移两边后,得到一个平行四边形吗?如果能得到平形四边形,那么能得到几个?分别用字母将它们表示出来。
A
B
C
D
E
F
画一画
A
D
C
B
O
ABCD中,对角线AC,BD交于O,EF过O交AD于E,交BC于F,
求证: OE=OF.
E
F
(P86:2)
探究3: ABCD中,对角线AC=4,BD=6,你能求出OA,OB,OC,OD吗?
平行四边形的性质:
平行四边形的对角线互相平分.
A
D
C
B
O
∵四边形ABCD是平行四边形
∴OA=OC= AC,
OB=OD= BD
1
2
1
2
对边(平行且)相等.
对角相等.
邻角互补.
对角线互相平分
2平行四边形的性质:
A
B
C
D
1定义.
两组对边分别平行的四边形叫做平行四边形.
∵四边形ABCD是 平行四边形
∴AD=BC,AB=DC
∠A=∠C,∠B=∠D
∠A+∠B=180°,∠B+∠C=180°
OA=OC= AC,
OB=OD= BD
1
2
1
2
O
课堂小结
仔细观察下面各图中蕴含着一种什么几何图形?
活动
你能用手中一对全等的三角形纸片拼出几个平行四边形?
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_____________________________________________
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
D
A
B
C
O
H
E
F
G
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形,
记作: ABCD
读作:平行四边形ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边
相对的角称为 对角
相 关 概 念
A
D
C
B
线段AC就是 ABCD的一条对角线
如图所示,用一对全等三角形拼出的这个四边形为什么是平行四边形呢?请说明理由.
A
B
C
D
根据定义可知平行四边形的对边互相平行。除此之外还有什么性质呢?这就是本节课要探讨的课题……
平行四边形的边、角有怎样的数量关系?
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
用你以前所学的知识证明猜想.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
几何语言:
定理1:平行四边形的对边相等
定理2:平行四边形的对角相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C,∠B=∠D.(平行四边形的对角相等)
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C,∠B=∠D.(平行四边形的对角相等)
A
B
C
D
如果已知平行四边形一个内角的度数,能确定其他三个内角的度数吗?说说你的理由。
通常四边形问题要转化为三角形问题.
平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的邻角互补.
平行四边形的性质
A
B
C
D
1
2
3
4
用符号语言表示:如图
A
B
C
D
ABCD
AD∥ BC, AB∥ DC
AD=BC, AB=DC
∠ A=∠ C, ∠ B=∠ D
小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。
1、在 ABCD中,已知∠A=130°,
则∠B=__ ,∠C=___ ,∠D=___.
2、在 ABCD中,AB=2,BC=3,
则这个平行四边形的周长是______.
课堂练习
50°
50°
130°
10
例1:如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
解:∵四边形ABCD是平行四边形,
∴∠A=∠C, ∠A+∠B=180°.
∵∠A+∠C=200°,
∴∠A=100°,∠B=80°.
⑴ 其他三条边各长多少?
随堂练习
1.在 ABCD中, AB=3cm,BC=8cm,则 ABCD的周长
是 cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3. ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
4.如图,在 ABCD中,∠B的平分线BE交AD于E,BC=5,
AB=3,则ED的长为 .
(第3题)
22
10cm,5cm
2
10
10
课堂小结
通过本节课的学习,你有哪些收获?
1.平行四边形的概念
两组对边分别平行的四边形叫做平行四边形
2.平行四边形的性质
平行四边形的对边平行且相等
平行四边形的对角相等
平行四边形的邻角互补。
3.解决平行四边形的有关问题经常连接对角线将
之转化为三角形的问题。
随堂练习1
如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝;
BC= ㎝;AD= ㎝。
2)若∠A=70°,则∠B= , ∠C= ; ∠D= 。
3)若∠A+∠C=80°,
则∠A= ; ∠D= 。
6
9
9
110°
70°
110°
40°
140°
1.已知: ABCD中,∠A=100°,你能求出其他各角的度数吗?说说你的理由.
∠B=80°
∠C=100°
∠ D=80°
A
D
C
B
随堂练习2
2.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
28
32
3cm
A
B
D
C
5cm
4cm
3.求如图所示的四边形ABCD的面积.
3cm
A
B
D
C
E
9cm
5cm
4.如图所示,若BE平分∠ABC,
则ED= .
4cm
2
3
5cm
5cm
4cm
1
比较线路长短
如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.
9
A
B
C
D
E
G
F
H
O
从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由.
上图的平行四边形ABCD中有几对全等三角形 有几对相等的线段
D
C
B
A
O
O
议一议
证明:
∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BAC
∴∠BAD=∠CAD
∵AB//EF ∴ ∠BAD=∠AEF
∴∠CAD =∠AEF ∴ AF=EF
∴ AF=BM
如图, 在 ABC中, AD平分∠BAC, 点M,E,F分别是AB,AD,AC上的点, 四边形BEFM是平行四边形. 求证:AF=BM
B
D
C
E
F
A
M
1.如图,四边形ABCD是平行四边形,填空
(1) ∠ADC=__,∠BCD=__
(2) ABCD的周长=____
B
A
D
C
30
20
50°
50°
130°
100
A
B
D
C
F
E
2.已知 ABCD,延长AB到E, 延长CD到F ,使BE=DF
求证: AF=CE
想一想做一做
A
B
D
C
F
E
2.已知 ABCD,延长AB到E, 延长CD到F ,使BE=DF, 求证: AF=CE
想一想做一做
1
2
3
4
∴ ADE≌ CBF(SAS)
解:∵ ABCD是平行四边形
∴AD=BC, ∠1=∠2
∵∠1+∠3=1800
∠2+∠4=1800
∴ ∠3= ∠4
∵ DF=BE
∴AF=CE
检测考试题
(1).在平行四边形ABCD中, ∠B=110°,延长AD至F,延长CD至E,连结EF, 求∠ E+∠ F.
(2). 在 ABCD中,连结BD, E,F是BD上的两点,且DE=BF, 求证: AE=CF.
D
F
A
B
C
E
E
F
∴ ∠B= ∠ADC=110°
∴ ∠EDF=110°
解:∵ ABCD是平行四边形
∵ ∠ADC=∠EDF
∴ ∠ E+ ∠F= 70°
(2). 在 ABCD中,连结BD, E,F是BD上的两点,且DE=BF, 求证: AE=CF.
E
F
∴ ADE≌ CBF
解:∵ ABCD是平行四边形
∴AD=BC
∵AD∥BC
∴ ∠ADE= ∠CBF
∵ DE=BF
∴AE=CF
检测考试题
(3).在 ABCD中,AE既是中线,又是高线,
如果 ABCD的周长为20cm, ABC的周长
比 ABCD的周长少6cm,
求 ABCD各边的长.
E
解: ∵ ABCD的周长为20cm ∴AB+BC=10cm
∵ ABC的周长比 ABCD的周长少6cm
∴AC= 4cm
∵ AE既是中线,又是高线
∴ AE 垂直平分BC, ∴AB= AC=4cm
∴CD=4cm BC=6cm AD=6cm
检测考试题
有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,
你能根据测得的数据计算
出DE的长度和∠D的度数吗?
AE∥BC
AB∥CF
四边形ABCD是平行四边形
∠B=60°
∠B=∠D
AD=BC=80
∠D=60°
DE=AD-AE
AE=60
DE=20cm
解:
课本P90, [习题19.1]
第1、2、6题。
预习课本P85~86的内容 。
课后作业
首页
上页
下页
知识与技能:
1、平行四边形的定义:两组对边分别
平行的四边形叫做平行四边形.
2、平行四边形的性质: 平行四边形的
对边平行且相等;平行四边形的对
角相等.
数学思想与方法:
1、“猜想——验证——证明”的科
学研究方法.
2、转化的数学思想.
感悟与收获
如图,在 ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长度?
F
D
C
B
A
E
活动与探究
首页
上页
下页
已知如图:E、F是平行四边形ABCD的对角线AC上的两点,AE=CF
求证:(1)△ADF≌ △CBE
(2)EB∥DF
1
2
3
4
已知:如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,BE平分∠ABC交AD于E,交CD的延长线于F.
⑴△ABE与△DFE全等吗?
A
B
C
D
E
F
⑵求CF的长.
⑶若连结CE,则CE与BE有怎样的位置关系?
⑷能否求出CE的长?
任画一个三角形,你能通过平移两边后,得到一个平行四边形吗?如果能得到平形四边形,那么能得到几个?分别用字母将它们表示出来。
A
B
C
D
E
F
画一画
A
D
C
B
O
ABCD中,对角线AC,BD交于O,EF过O交AD于E,交BC于F,
求证: OE=OF.
E
F
(P86:2)
探究3: ABCD中,对角线AC=4,BD=6,你能求出OA,OB,OC,OD吗?
平行四边形的性质:
平行四边形的对角线互相平分.
A
D
C
B
O
∵四边形ABCD是平行四边形
∴OA=OC= AC,
OB=OD= BD
1
2
1
2
对边(平行且)相等.
对角相等.
邻角互补.
对角线互相平分
2平行四边形的性质:
A
B
C
D
1定义.
两组对边分别平行的四边形叫做平行四边形.
∵四边形ABCD是 平行四边形
∴AD=BC,AB=DC
∠A=∠C,∠B=∠D
∠A+∠B=180°,∠B+∠C=180°
OA=OC= AC,
OB=OD= BD
1
2
1
2
O
课堂小结
