江苏省师范大学培栋中学2020-2021学年高一下学期6月第一次练习数学试题 Word版含答案
文档属性
| 名称 | 江苏省师范大学培栋中学2020-2021学年高一下学期6月第一次练习数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 837.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 16:36:00 | ||
图片预览



文档简介
培栋中学高一年级6月份第一次练习
一、选择题.本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1. (2021高考题)设集合A= {x|-2A.{2} B.{2,3} C.{3,4,} D.{2,3,4}
2.(2021高考题)已知z=2-i,则= ( )
A.6-2i B.4-2i C.6+2i D.4+2i
3.(2021高考题)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为 ( )
A.2 B.2 C.4 D.4
4.(2021高考题)下列区间中,函数单调递增的区间是 ( )
A.(0,) B.( ,) C.(,) D.(,)
5.阿基米德(Archimedes,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为,则圆柱的表面积为 ( )
A. B. C. D.
6.如图,边长为1的正方形是一个水平放置的平面图形的直观图,则平面图形以为轴旋转一周所围成的几何体的体积为( )
A. B. C. D.
7.已知是相互垂直的单位向量,与共面的向量满足则的模为( )
A. B. C. D.
8.(2021高考题)若则= ( )
A. B. C. D.
二、选择题∶本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分。
9.(2021高考题)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中
yi=xi+c(i=1,2,…,n),c为非零常数,则 ( )
A.两组样本数据的样本平均数相同 B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同 D.两组样本数据的样本极差相同
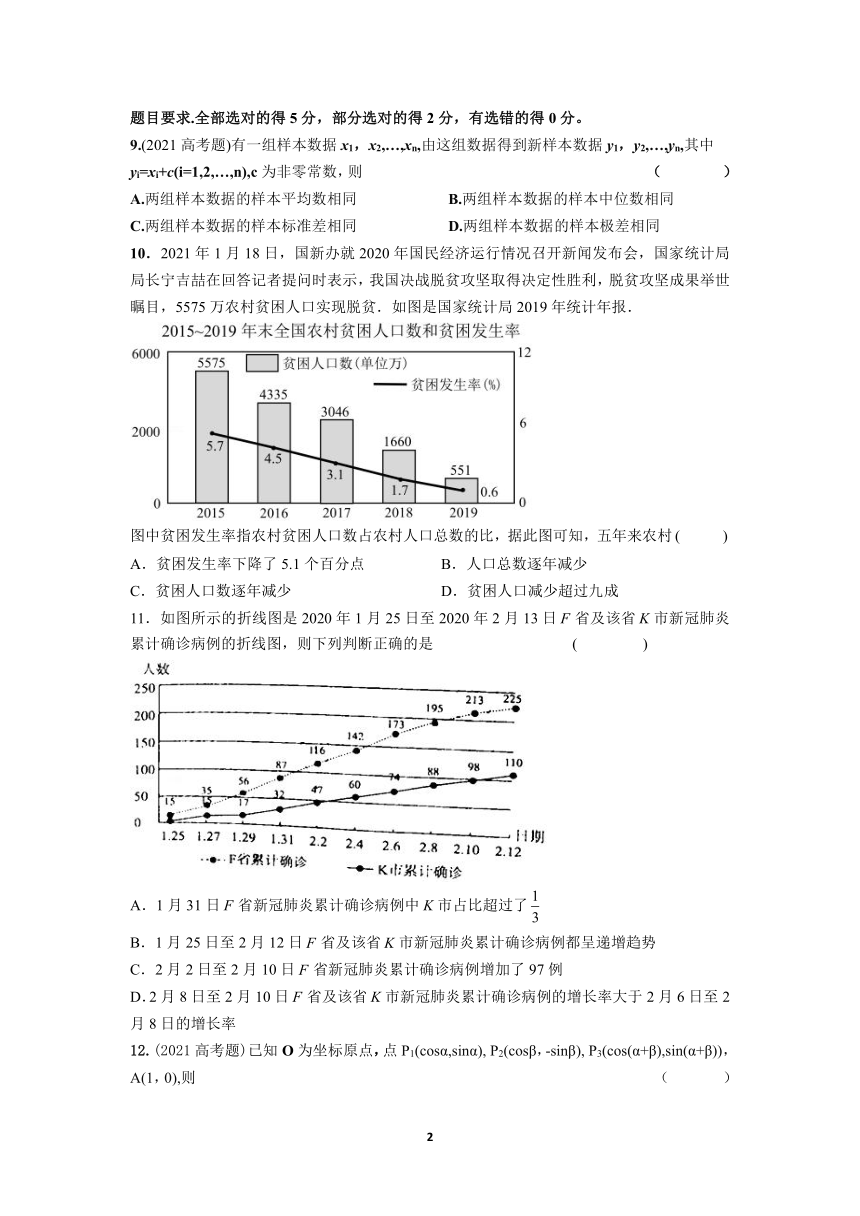
10.2021年1月18日,国新办就2020年国民经济运行情况召开新闻发布会,国家统计局局长宁吉喆在回答记者提问时表示,我国决战脱贫攻坚取得决定性胜利,脱贫攻坚成果举世瞩目,5575万农村贫困人口实现脱贫.如图是国家统计局2019年统计年报.
图中贫困发生率指农村贫困人口数占农村人口总数的比,据此图可知,五年来农村
A.贫困发生率下降了5.1个百分点 B.人口总数逐年减少
C.贫困人口数逐年减少 D.贫困人口减少超过九成
11.如图所示的折线图是2020年1月25日至2020年2月13日省及该省市新冠肺炎累计确诊病例的折线图,则下列判断正确的是
A.1月31日省新冠肺炎累计确诊病例中市占比超过了
B.1月25日至2月12日省及该省市新冠肺炎累计确诊病例都呈递增趋势
C.2月2日至2月10日省新冠肺炎累计确诊病例增加了97例
D.2月8日至2月10日省及该省市新冠肺炎累计确诊病例的增长率大于2月6日至2月8日的增长率
12.(2021高考题)已知O为坐标原点,点P1(cosα,sinα), P2(cosβ,-sinβ), P3(cos(α+β),sin(α+β)),A(1,0),则 ( )
A.|= B.=
C.= D.
三、填空题∶本题共4小题,每小题5分,共20分。
13.有一塔形空间图形由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,则该塔形空间图形的表面积(含最底层正方体的底面面积)为________.
14.在△ABC中,sin2A≤sin2B+sin2C-sin Bsin C,则A的取值范围是________.
15.已知函数f(x)=cos2-sin2+sin x,若x0∈且f(x0)=,则cos 2x0=________.
16.已知平面α∥平面β,直线mα,直线nβ,点A∈m,点B∈n,记点A,B之间的距离为a,点A到直线n的距离为b,直线m和n的距离为c,则a,b,c之间的大小关系为__________.
解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.如图,长方体中,,P是棱上的动点.
(1)若E,F分别是的中点,证明:平面;
(2)求三棱锥的体积.
18.已知z是复数,z+2i、均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
19.已知a,b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,求a与b的夹角.
20.已知函数f(x)=2-sin(x+π).
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
21.在△ABC中,角A,B,C所对的边分别为a,b,c.
(1)若(a+b+c)(b+c-a)=3bc,求A的值;
(2)若c=10,A=45°,C=30°,求b的值.
22.如图,在正方体中,点为棱的中点.
(1)求证:平面;
(2)求异面直线与所成角的余弦值.
培栋中学高一年级6月份第一次练习
一、选择题。本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. (2021高考题)设集合A= {x|-2A.{2} B.{2,3} C.{3,4,} D.{2,3,4}
2.(2021高考题)已知z=2-i,则= ( C )
A.6-2i B.4-2i C.6+2i D.4+2i
3.(2021高考题)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为 ( B )
A.2 B.2 C.4 D.4
4.(2021高考题)下列区间中,函数单调递增的区间是 ( A )
A.(0,) B.( ,) C.(,) D.(,)
5.阿基米德(Archimedes,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为,则圆柱的表面积为( C )
A. B. C. D.
6.如图,边长为1的正方形是一个水平放置的平面图形的直观图,则平面图形以为轴旋转一周所围成的几何体的体积为( C )
A. B. C. D.
7.已知是相互垂直的单位向量,与共面的向量满足则的模为( D )
A. B. C. D.
解:是相互垂直的单位向量,不妨设,,设,由 可得,即,则的模为. 故选:D
8.(2021高考题)若则= ( C )
A. B. C. D.
二、选择题∶本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.(2021高考题)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中
yi=xi+c(i=1,2,…,n),c为非零常数,则 ( CD )
A.两组样本数据的样本平均数相同 B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同 D.两组样本数据的样本极差相同
10.2021年1月18日,国新办就2020年国民经济运行情况召开新闻发布会,国家统计局局长宁吉喆在回答记者提问时表示,我国决战脱贫攻坚取得决定性胜利,脱贫攻坚成果举世瞩目,5575万农村贫困人口实现脱贫.如图是国家统计局2019年统计年报.
图中贫困发生率指农村贫困人口数占农村人口总数的比,据此图可知,五年来农村ACD
A.贫困发生率下降了5.1个百分点 B.人口总数逐年减少
C.贫困人口数逐年减少 D.贫困人口减少超过九成
11.如图所示的折线图是2020年1月25日至2020年2月13日省及该省市新冠肺炎累计确诊病例的折线图,则下列判断正确的是 ABC
A.1月31日省新冠肺炎累计确诊病例中市占比超过了
B.1月25日至2月12日省及该省市新冠肺炎累计确诊病例都呈递增趋势
C.2月2日至2月10日省新冠肺炎累计确诊病例增加了97例
D.2月8日至2月10日省及该省市新冠肺炎累计确诊病例的增长率大于2月6日至2月8日的增长率
12.(2021高考题)已知O为坐标原点,点P1(cosα,sinα), P2(cosβ,-sinβ), P3(cos(α+β),sin(α+β)),A(1,0),则 ( AC )
A.|= B.=
C.= D.
三、填空题∶本题共4小题,每小题5分,共20分。
13.有一塔形空间图形由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,则该塔形空间图形的表面积(含最底层正方体的底面面积)为_____36___.
解:由题意可知,由下向上三个正方体的棱长依次为2,,1,∴S表=2×22+4×[22+()2+12]=36.∴该空间图形的表面积为36,故答案为:36
14.在△ABC中,sin2A≤sin2B+sin2C-sin Bsin C,则A的取值范围是________.[0,]
解:由题意和正弦定理,得a2≤b2+c2-bc,∴b2+c2-a2≥bc,cos A=≥
15.已知函数f(x)=cos2-sin2+sin x,若x0∈且f(x0)=,则cos 2x0=________.
解:f(x)=cos x+sin x=sin,由f(x0)=,得sin=.又x0∈,所以x0+∈,所以cos=,所以cos 2x0=sin=2sincos=.
16.已知平面α∥平面β,直线mα,直线nβ,点A∈m,点B∈n,记点A,B之间的距离为a,点A到直线n的距离为b,直线m和n的距离为c,则a,b,c之间的大小关系为__________.
解:c≤b≤a [在如图所示的棱长为1的正方体中,上、下底面分别记为α,β.直线m即直线AD1,直线n即直线BD.显然点A,B之间的距离为a=,点A到直线n的距离为b=,直线m和n的距离为c=1,则c解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。
17.如图,长方体中,,P是棱上的动点.
(1)若E,F分别是的中点,
证明:平面;
(2)求三棱锥的体积.
证明(1)E,F分别是的中点,,又平面,平面,平面;
(2)作于,则为三棱锥的高,且,;
18.已知z是复数,z+2i、均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
解:设z=x+yi(x、y∈R),所以z+2i=x+(y+2)i,由题意得y=-2.因为==(x-2i)(2+i)=(2x+2)+(x-4)i.由题意得x=4,所以z=4-2i.所以(z+ai)2=(12+4a-a2)+8(a-2)i,由于(z+ai)2在复平面上对应的点在第一象限,所以解得219.已知a,b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,求a与b的夹角.
解:由已知,得(a+3b)·(7a-5b)=0,即7a2+16a·b-15b2=0,①
(a-4b)·(7a-2b)=0,即7a2-30a·b+8b2=0,②
①②两式相减,得2a·b=b2,∴a·b=b2,代入①②中任一式,得a2=b2,设a,b的夹角为θ,则cos θ===,∵0°≤θ≤180°,∴θ=60°.
20.已知函数f(x)=2-sin(x+π).
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
解:(1)因为f(x)=sin+sin x=cos x+sin x=2sin,所以f(x)的最小正周期为2π.(2)因为g(x)=f=2sin=2sin,且x∈[0,π],所以x+∈,所以当x+=,即x=时,g(x)取最大值2;当x+=,即x=π时,g(x)取最小值-2.
21.在△ABC中,角A,B,C所对的边分别为a,b,c.
(1)若(a+b+c)(b+c-a)=3bc,求A的值;
(2)若c=10,A=45°,C=30°,求b的值.
解:(1)由已知得(b+c)2-a2=3bc,即a2=b2+c2-bc.由余弦定理a2=b2+c2-2bccos A,得cos A=.由于0(2)由于A+B+C=180°,所以B=180°-45°-30°=105°.由正弦定理=,得b=·sin B=·sin 105°=20×=5(+).
22.如图,在正方体中,点为棱的中点.
(1)求证:平面;
(2)求异面直线与所成角的余弦值.
证明:(1)如图所示:连接BD与AC交于点O,因为O,E为为中点,所以,又平面,平面,所以平面;
(2)由(1)知,则异面直线与所成的角,
在正方体中,因为,且,所以平面,又因为平面,所以 ,所以是直角三角形,设正方体的棱长为a,则 , ,所以 ,所以,故答案为:
一、选择题.本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1. (2021高考题)设集合A= {x|-2
2.(2021高考题)已知z=2-i,则= ( )
A.6-2i B.4-2i C.6+2i D.4+2i
3.(2021高考题)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为 ( )
A.2 B.2 C.4 D.4
4.(2021高考题)下列区间中,函数单调递增的区间是 ( )
A.(0,) B.( ,) C.(,) D.(,)
5.阿基米德(Archimedes,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为,则圆柱的表面积为 ( )
A. B. C. D.
6.如图,边长为1的正方形是一个水平放置的平面图形的直观图,则平面图形以为轴旋转一周所围成的几何体的体积为( )
A. B. C. D.
7.已知是相互垂直的单位向量,与共面的向量满足则的模为( )
A. B. C. D.
8.(2021高考题)若则= ( )
A. B. C. D.
二、选择题∶本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分。
9.(2021高考题)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中
yi=xi+c(i=1,2,…,n),c为非零常数,则 ( )
A.两组样本数据的样本平均数相同 B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同 D.两组样本数据的样本极差相同
10.2021年1月18日,国新办就2020年国民经济运行情况召开新闻发布会,国家统计局局长宁吉喆在回答记者提问时表示,我国决战脱贫攻坚取得决定性胜利,脱贫攻坚成果举世瞩目,5575万农村贫困人口实现脱贫.如图是国家统计局2019年统计年报.
图中贫困发生率指农村贫困人口数占农村人口总数的比,据此图可知,五年来农村
A.贫困发生率下降了5.1个百分点 B.人口总数逐年减少
C.贫困人口数逐年减少 D.贫困人口减少超过九成
11.如图所示的折线图是2020年1月25日至2020年2月13日省及该省市新冠肺炎累计确诊病例的折线图,则下列判断正确的是
A.1月31日省新冠肺炎累计确诊病例中市占比超过了
B.1月25日至2月12日省及该省市新冠肺炎累计确诊病例都呈递增趋势
C.2月2日至2月10日省新冠肺炎累计确诊病例增加了97例
D.2月8日至2月10日省及该省市新冠肺炎累计确诊病例的增长率大于2月6日至2月8日的增长率
12.(2021高考题)已知O为坐标原点,点P1(cosα,sinα), P2(cosβ,-sinβ), P3(cos(α+β),sin(α+β)),A(1,0),则 ( )
A.|= B.=
C.= D.
三、填空题∶本题共4小题,每小题5分,共20分。
13.有一塔形空间图形由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,则该塔形空间图形的表面积(含最底层正方体的底面面积)为________.
14.在△ABC中,sin2A≤sin2B+sin2C-sin Bsin C,则A的取值范围是________.
15.已知函数f(x)=cos2-sin2+sin x,若x0∈且f(x0)=,则cos 2x0=________.
16.已知平面α∥平面β,直线mα,直线nβ,点A∈m,点B∈n,记点A,B之间的距离为a,点A到直线n的距离为b,直线m和n的距离为c,则a,b,c之间的大小关系为__________.
解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.如图,长方体中,,P是棱上的动点.
(1)若E,F分别是的中点,证明:平面;
(2)求三棱锥的体积.
18.已知z是复数,z+2i、均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
19.已知a,b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,求a与b的夹角.
20.已知函数f(x)=2-sin(x+π).
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
21.在△ABC中,角A,B,C所对的边分别为a,b,c.
(1)若(a+b+c)(b+c-a)=3bc,求A的值;
(2)若c=10,A=45°,C=30°,求b的值.
22.如图,在正方体中,点为棱的中点.
(1)求证:平面;
(2)求异面直线与所成角的余弦值.
培栋中学高一年级6月份第一次练习
一、选择题。本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. (2021高考题)设集合A= {x|-2
2.(2021高考题)已知z=2-i,则= ( C )
A.6-2i B.4-2i C.6+2i D.4+2i
3.(2021高考题)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为 ( B )
A.2 B.2 C.4 D.4
4.(2021高考题)下列区间中,函数单调递增的区间是 ( A )
A.(0,) B.( ,) C.(,) D.(,)
5.阿基米德(Archimedes,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径,若球的体积为,则圆柱的表面积为( C )
A. B. C. D.
6.如图,边长为1的正方形是一个水平放置的平面图形的直观图,则平面图形以为轴旋转一周所围成的几何体的体积为( C )
A. B. C. D.
7.已知是相互垂直的单位向量,与共面的向量满足则的模为( D )
A. B. C. D.
解:是相互垂直的单位向量,不妨设,,设,由 可得,即,则的模为. 故选:D
8.(2021高考题)若则= ( C )
A. B. C. D.
二、选择题∶本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.(2021高考题)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中
yi=xi+c(i=1,2,…,n),c为非零常数,则 ( CD )
A.两组样本数据的样本平均数相同 B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同 D.两组样本数据的样本极差相同
10.2021年1月18日,国新办就2020年国民经济运行情况召开新闻发布会,国家统计局局长宁吉喆在回答记者提问时表示,我国决战脱贫攻坚取得决定性胜利,脱贫攻坚成果举世瞩目,5575万农村贫困人口实现脱贫.如图是国家统计局2019年统计年报.
图中贫困发生率指农村贫困人口数占农村人口总数的比,据此图可知,五年来农村ACD
A.贫困发生率下降了5.1个百分点 B.人口总数逐年减少
C.贫困人口数逐年减少 D.贫困人口减少超过九成
11.如图所示的折线图是2020年1月25日至2020年2月13日省及该省市新冠肺炎累计确诊病例的折线图,则下列判断正确的是 ABC
A.1月31日省新冠肺炎累计确诊病例中市占比超过了
B.1月25日至2月12日省及该省市新冠肺炎累计确诊病例都呈递增趋势
C.2月2日至2月10日省新冠肺炎累计确诊病例增加了97例
D.2月8日至2月10日省及该省市新冠肺炎累计确诊病例的增长率大于2月6日至2月8日的增长率
12.(2021高考题)已知O为坐标原点,点P1(cosα,sinα), P2(cosβ,-sinβ), P3(cos(α+β),sin(α+β)),A(1,0),则 ( AC )
A.|= B.=
C.= D.
三、填空题∶本题共4小题,每小题5分,共20分。
13.有一塔形空间图形由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,则该塔形空间图形的表面积(含最底层正方体的底面面积)为_____36___.
解:由题意可知,由下向上三个正方体的棱长依次为2,,1,∴S表=2×22+4×[22+()2+12]=36.∴该空间图形的表面积为36,故答案为:36
14.在△ABC中,sin2A≤sin2B+sin2C-sin Bsin C,则A的取值范围是________.[0,]
解:由题意和正弦定理,得a2≤b2+c2-bc,∴b2+c2-a2≥bc,cos A=≥
15.已知函数f(x)=cos2-sin2+sin x,若x0∈且f(x0)=,则cos 2x0=________.
解:f(x)=cos x+sin x=sin,由f(x0)=,得sin=.又x0∈,所以x0+∈,所以cos=,所以cos 2x0=sin=2sincos=.
16.已知平面α∥平面β,直线mα,直线nβ,点A∈m,点B∈n,记点A,B之间的距离为a,点A到直线n的距离为b,直线m和n的距离为c,则a,b,c之间的大小关系为__________.
解:c≤b≤a [在如图所示的棱长为1的正方体中,上、下底面分别记为α,β.直线m即直线AD1,直线n即直线BD.显然点A,B之间的距离为a=,点A到直线n的距离为b=,直线m和n的距离为c=1,则c
17.如图,长方体中,,P是棱上的动点.
(1)若E,F分别是的中点,
证明:平面;
(2)求三棱锥的体积.
证明(1)E,F分别是的中点,,又平面,平面,平面;
(2)作于,则为三棱锥的高,且,;
18.已知z是复数,z+2i、均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
解:设z=x+yi(x、y∈R),所以z+2i=x+(y+2)i,由题意得y=-2.因为==(x-2i)(2+i)=(2x+2)+(x-4)i.由题意得x=4,所以z=4-2i.所以(z+ai)2=(12+4a-a2)+8(a-2)i,由于(z+ai)2在复平面上对应的点在第一象限,所以解得2
解:由已知,得(a+3b)·(7a-5b)=0,即7a2+16a·b-15b2=0,①
(a-4b)·(7a-2b)=0,即7a2-30a·b+8b2=0,②
①②两式相减,得2a·b=b2,∴a·b=b2,代入①②中任一式,得a2=b2,设a,b的夹角为θ,则cos θ===,∵0°≤θ≤180°,∴θ=60°.
20.已知函数f(x)=2-sin(x+π).
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
解:(1)因为f(x)=sin+sin x=cos x+sin x=2sin,所以f(x)的最小正周期为2π.(2)因为g(x)=f=2sin=2sin,且x∈[0,π],所以x+∈,所以当x+=,即x=时,g(x)取最大值2;当x+=,即x=π时,g(x)取最小值-2.
21.在△ABC中,角A,B,C所对的边分别为a,b,c.
(1)若(a+b+c)(b+c-a)=3bc,求A的值;
(2)若c=10,A=45°,C=30°,求b的值.
解:(1)由已知得(b+c)2-a2=3bc,即a2=b2+c2-bc.由余弦定理a2=b2+c2-2bccos A,得cos A=.由于0
22.如图,在正方体中,点为棱的中点.
(1)求证:平面;
(2)求异面直线与所成角的余弦值.
证明:(1)如图所示:连接BD与AC交于点O,因为O,E为为中点,所以,又平面,平面,所以平面;
(2)由(1)知,则异面直线与所成的角,
在正方体中,因为,且,所以平面,又因为平面,所以 ,所以是直角三角形,设正方体的棱长为a,则 , ,所以 ,所以,故答案为:
同课章节目录
