3.2.2_双曲线的简单几何性质-【新教材】人教A版(2019)高中数学选择性必修第一册课件(26张PPT)
文档属性
| 名称 | 3.2.2_双曲线的简单几何性质-【新教材】人教A版(2019)高中数学选择性必修第一册课件(26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 920.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 17:06:50 | ||
图片预览








文档简介
(共26张PPT)
2.3.2 双曲线简单的几何性质
思考回顾
椭圆的简单几何性质 ?
①范围; ②对称性; ③顶点;
④离心率等
双曲线是否具有类似的性质呢
回想:我们是怎样研究上述性质的?
2、对称性
一、研究双曲线 的简单几何性质
1、范围
关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
课堂新授
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长
(2)
实轴与虚轴等长的双曲线
叫等轴双曲线
(3)
M(x,y)
4、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
利用渐近线可以较准确的
画出双曲线的草图
(2)
5、离心率
离心率。
c>a>0
e >1
e是表示双曲线开口大小的一个量,e越大开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
x
y
o
-a
a
b
-b
(1)范围:
(2)对称性:
关于x轴、y轴、原点都对称
(3)顶点:
(0,-a)、(0,a)
(4)渐近线:
(5)离心率:
例1 :求双曲线
的实半轴长,虚半轴长,
焦点坐标,离心率、渐近线方程。
解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3
半焦距c=
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
5
3
4
2
2
=
+
4
5
=
=
a
c
e
例题讲解
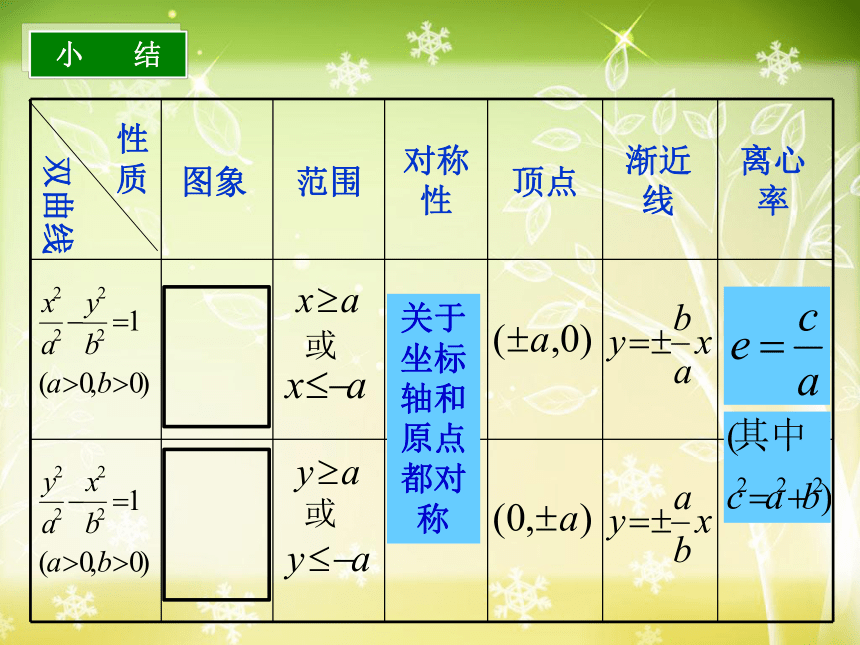
小 结
或
或
关于坐标
轴和
原点
都对
称
性质
双曲线
范围
对称
性
顶点
渐近
线
离心
率
图象
▲思考:(3)两种双曲线的渐近线方程,怎样统一记忆?(1)双曲线 的渐近线方程是什么? (2)双曲线 的渐近线方程是什么?的渐近线方程为:的渐近线方程为:的渐近线方程为:的渐近线方程为:的渐近线方程为:1、“共渐近线”的双曲线的应用
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
总结:
oxy解:(3)已知双曲线的渐近线是 ,并且双曲线过点,求双曲线方程。Q4M1)2)(3)已知双曲线的渐近线是 ,并且双曲线过点,求双曲线方程。1、若双曲线 的渐近线方程为
则双曲线的离心率为 。
2、若双曲线 的离心率为2,则两条渐
近线的夹角为 。
例3、点M(x,y)与定点F(5,0),的距离
和它到定直线 : 的距离的比是常
数 , 求点M的轨迹.
y
0
d
x
y
O
l
F
引例:点M(x, y)与定点F(c, 0)的距离和它到定直线
的距离比是常数 (c>a>0),求点M的轨迹.
M
解:
设点M(x,y)到l的距离为d,则
即
化简得
(c2-a2)x2- a2y2=a2 (c2 - a2)
设c2-a2 =b2,
(a>0,b>0)
故点M的轨迹为实轴、虚轴长分别为2a、2b的双曲线.
b2x2-a2y2=a2b2
即
就可化为:
M
点M的轨迹也包括双曲线的左支.
第二定义
例、双曲线型自然通风塔的外形,是双曲线
的一部分绕其虚轴旋转所成的曲面,它的
最小半径为12m,上口半径为13m,下口半径
为25m,高55m.选择适当的坐标系,求出此
双曲线的方程(精确到1m).
A′
A
0
x
C′
C
B′
B
y
13
12
25
例题讲解
1
2
=
+
b
y
a
x
2
2
2
( a> b >0)
1
2
2
2
2
=
-
b
y
a
x
( a> 0 b>0)
2
2
2
=
+
b
a
(a> 0 b>0)
c
2
2
2
=
-
b
a
(a> b>0)
c
椭 圆 双曲线
方程
a b c关系
图象
椭圆与双曲线的比较
y
X
F1
0
F2
M
X
Y
0
F1
F2
p
小 结
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐近线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
2.3.2 双曲线简单的几何性质
思考回顾
椭圆的简单几何性质 ?
①范围; ②对称性; ③顶点;
④离心率等
双曲线是否具有类似的性质呢
回想:我们是怎样研究上述性质的?
2、对称性
一、研究双曲线 的简单几何性质
1、范围
关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
课堂新授
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长
(2)
实轴与虚轴等长的双曲线
叫等轴双曲线
(3)
M(x,y)
4、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
利用渐近线可以较准确的
画出双曲线的草图
(2)
5、离心率
离心率。
c>a>0
e >1
e是表示双曲线开口大小的一个量,e越大开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
x
y
o
-a
a
b
-b
(1)范围:
(2)对称性:
关于x轴、y轴、原点都对称
(3)顶点:
(0,-a)、(0,a)
(4)渐近线:
(5)离心率:
例1 :求双曲线
的实半轴长,虚半轴长,
焦点坐标,离心率、渐近线方程。
解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3
半焦距c=
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
5
3
4
2
2
=
+
4
5
=
=
a
c
e
例题讲解
小 结
或
或
关于坐标
轴和
原点
都对
称
性质
双曲线
范围
对称
性
顶点
渐近
线
离心
率
图象
▲思考:(3)两种双曲线的渐近线方程,怎样统一记忆?(1)双曲线 的渐近线方程是什么? (2)双曲线 的渐近线方程是什么?的渐近线方程为:的渐近线方程为:的渐近线方程为:的渐近线方程为:的渐近线方程为:1、“共渐近线”的双曲线的应用
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
总结:
oxy解:(3)已知双曲线的渐近线是 ,并且双曲线过点,求双曲线方程。Q4M1)2)(3)已知双曲线的渐近线是 ,并且双曲线过点,求双曲线方程。1、若双曲线 的渐近线方程为
则双曲线的离心率为 。
2、若双曲线 的离心率为2,则两条渐
近线的夹角为 。
例3、点M(x,y)与定点F(5,0),的距离
和它到定直线 : 的距离的比是常
数 , 求点M的轨迹.
y
0
d
x
y
O
l
F
引例:点M(x, y)与定点F(c, 0)的距离和它到定直线
的距离比是常数 (c>a>0),求点M的轨迹.
M
解:
设点M(x,y)到l的距离为d,则
即
化简得
(c2-a2)x2- a2y2=a2 (c2 - a2)
设c2-a2 =b2,
(a>0,b>0)
故点M的轨迹为实轴、虚轴长分别为2a、2b的双曲线.
b2x2-a2y2=a2b2
即
就可化为:
M
点M的轨迹也包括双曲线的左支.
第二定义
例、双曲线型自然通风塔的外形,是双曲线
的一部分绕其虚轴旋转所成的曲面,它的
最小半径为12m,上口半径为13m,下口半径
为25m,高55m.选择适当的坐标系,求出此
双曲线的方程(精确到1m).
A′
A
0
x
C′
C
B′
B
y
13
12
25
例题讲解
1
2
=
+
b
y
a
x
2
2
2
( a> b >0)
1
2
2
2
2
=
-
b
y
a
x
( a> 0 b>0)
2
2
2
=
+
b
a
(a> 0 b>0)
c
2
2
2
=
-
b
a
(a> b>0)
c
椭 圆 双曲线
方程
a b c关系
图象
椭圆与双曲线的比较
y
X
F1
0
F2
M
X
Y
0
F1
F2
p
小 结
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐近线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
