3.3.1抛物线及其标准方程-【新教材】人教A版(2019)高中数学选择性必修第一册课件(20张PPT)
文档属性
| 名称 | 3.3.1抛物线及其标准方程-【新教材】人教A版(2019)高中数学选择性必修第一册课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 462.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 17:08:16 | ||
图片预览





文档简介
抛物线极其标准方程
抛物线的生活实例
抛球运动
F
l
M1
M
M2
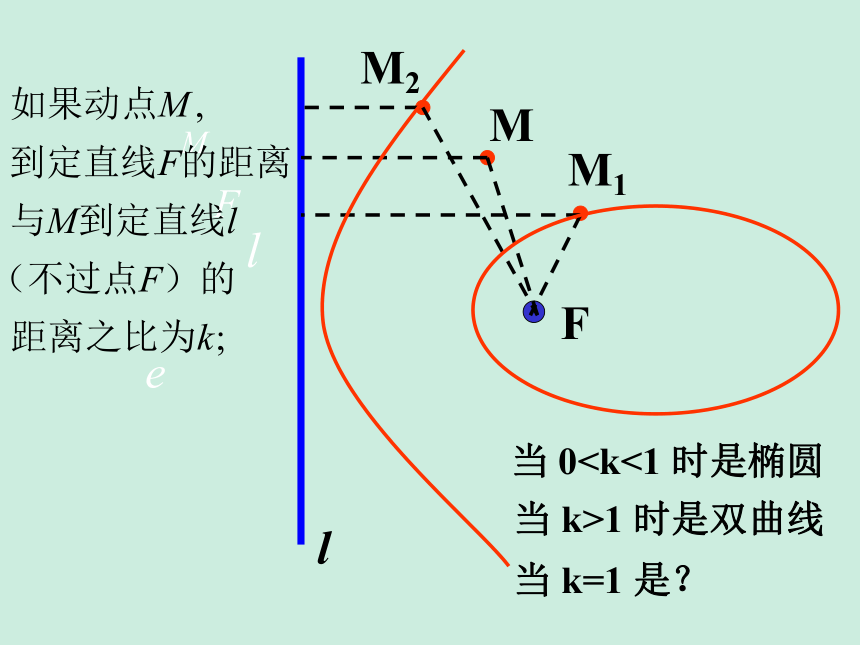
当 0当 k>1 时是双曲线
当 k=1 是?
画抛物线
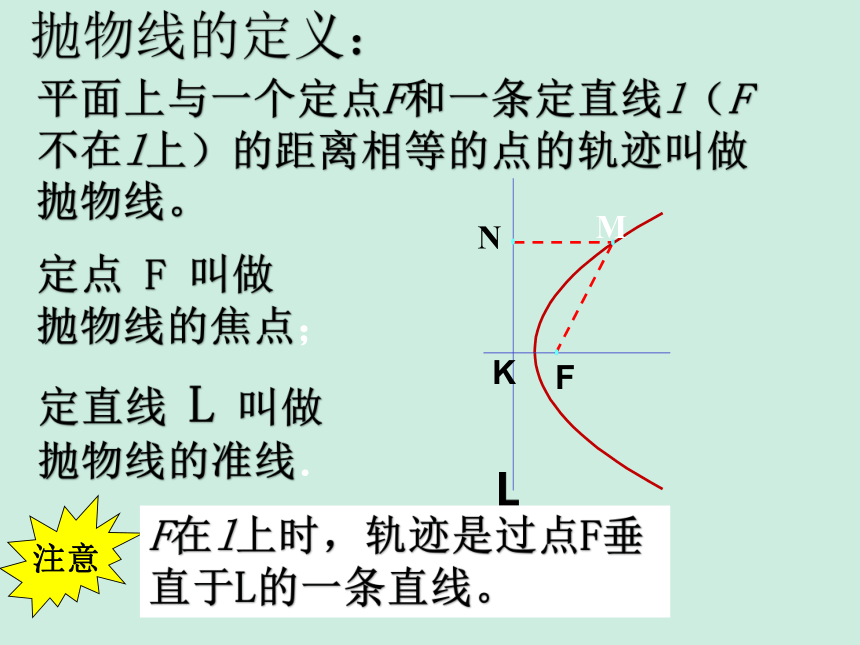
抛物线的定义:
定点 F 叫做 抛物线的焦点;
定直线 L 叫做抛物线的准线.
L
F
K
M
N
平面上与一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线。
注意
F在l上时,轨迹是过点F垂直于L的一条直线。
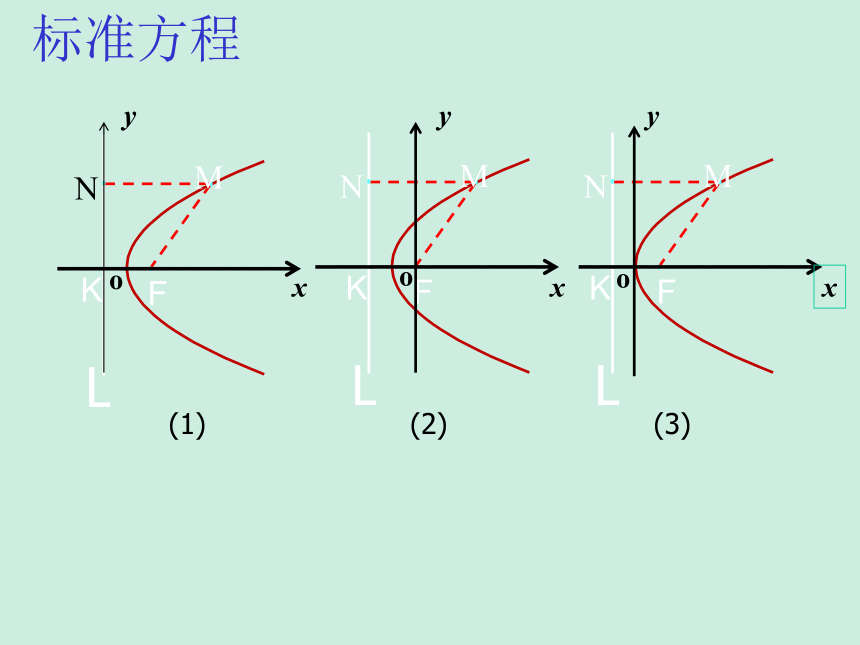
二、标准方程
·
·
F
M
l
N
如何建立直角
坐标系?
想一想?
求曲线方程的基本步骤是怎样的?
步骤:(1)建系(2)设点(3)列式(4)化简(5)检验
标准方程
(1)
(2)
(3)
L
F
K
M
N
L
F
K
M
N
L
F
K
M
N
x
x
x
y
y
y
o
o
o
二、标准方程
x
y
o
·
·
F
M
l
N
K
1、建系
2、设点
3、列式
4、化简
方程 y2 = 2px(p>0)叫做抛物线的标准方程
其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离
抛物线及其标准方程
一.定义:平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线。定点F叫做抛物线的焦点定直线l 叫做抛物线的准线。
二.标准方程:
y
o
x
·
·
F
M
l
N
K
则F( ,0),l:x = -
p
2
p
2
一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.
方程y2 = 2px(p>0)表示抛物线的焦点在 X轴的正半轴上
抛物线的标准方程还有几种不同的形式?它们是如何建系的?
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
图 形
焦 点
准 线
标准方程
根据上表中抛物线的标准方程的不同 形式与图形、焦点坐标、准线方程对应关系,如何判断抛物线的焦点位置,开口方向?
想一想:
第一:一次项的变量为抛物线的对 称轴,焦点就在对称轴上;
第二:一次项系数的正负决定了抛 物线的开口方向.
例1(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。
解:因为p=3,故焦点坐标为(-,0)
准线方程为x=- -.
32
32
1 12
解:方程可化为:x =- -y,故p=-,焦点坐标
为(0, --),准线方程为y= -.
16
1 24
1 24
2
解:因焦点在y轴的负半轴上,且p=4,故其标准方程为:x = - 8y
2
练习:
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程 是x = ;
(3)焦点到准 线的距离是2。
y2 =12x
y2 =x
y2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y
2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y (3)x2 +8y =0
焦点坐标
准线方程
(1)
(2)
(3)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
y=2
(0 , -2)
例2、求过点A(-3,2)的抛物线的
标准方程。
.
A
O
y
x
解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p=
当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
二次函数的图像为什么是抛物线?
例3,一种卫星接收天线如图所示,其曲面与轴截面的交线为抛物线,在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚焦到焦点处,如图1,已知接受天线的口径(直径)为4.8m,深度为1m,试建立适当的坐标系,求抛物线的标准方程和焦点坐标。
O
y
x
F
A
B
抛物线的生活实例
抛球运动
F
l
M1
M
M2
当 0
当 k=1 是?
画抛物线
抛物线的定义:
定点 F 叫做 抛物线的焦点;
定直线 L 叫做抛物线的准线.
L
F
K
M
N
平面上与一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线。
注意
F在l上时,轨迹是过点F垂直于L的一条直线。
二、标准方程
·
·
F
M
l
N
如何建立直角
坐标系?
想一想?
求曲线方程的基本步骤是怎样的?
步骤:(1)建系(2)设点(3)列式(4)化简(5)检验
标准方程
(1)
(2)
(3)
L
F
K
M
N
L
F
K
M
N
L
F
K
M
N
x
x
x
y
y
y
o
o
o
二、标准方程
x
y
o
·
·
F
M
l
N
K
1、建系
2、设点
3、列式
4、化简
方程 y2 = 2px(p>0)叫做抛物线的标准方程
其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离
抛物线及其标准方程
一.定义:平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线。定点F叫做抛物线的焦点定直线l 叫做抛物线的准线。
二.标准方程:
y
o
x
·
·
F
M
l
N
K
则F( ,0),l:x = -
p
2
p
2
一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.
方程y2 = 2px(p>0)表示抛物线的焦点在 X轴的正半轴上
抛物线的标准方程还有几种不同的形式?它们是如何建系的?
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
图 形
焦 点
准 线
标准方程
根据上表中抛物线的标准方程的不同 形式与图形、焦点坐标、准线方程对应关系,如何判断抛物线的焦点位置,开口方向?
想一想:
第一:一次项的变量为抛物线的对 称轴,焦点就在对称轴上;
第二:一次项系数的正负决定了抛 物线的开口方向.
例1(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。
解:因为p=3,故焦点坐标为(-,0)
准线方程为x=- -.
32
32
1 12
解:方程可化为:x =- -y,故p=-,焦点坐标
为(0, --),准线方程为y= -.
16
1 24
1 24
2
解:因焦点在y轴的负半轴上,且p=4,故其标准方程为:x = - 8y
2
练习:
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程 是x = ;
(3)焦点到准 线的距离是2。
y2 =12x
y2 =x
y2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y
2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y (3)x2 +8y =0
焦点坐标
准线方程
(1)
(2)
(3)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
y=2
(0 , -2)
例2、求过点A(-3,2)的抛物线的
标准方程。
.
A
O
y
x
解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p=
当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
二次函数的图像为什么是抛物线?
例3,一种卫星接收天线如图所示,其曲面与轴截面的交线为抛物线,在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚焦到焦点处,如图1,已知接受天线的口径(直径)为4.8m,深度为1m,试建立适当的坐标系,求抛物线的标准方程和焦点坐标。
O
y
x
F
A
B
