3.3.2直线与抛物线的位置关系-【新教材】人教A版(2019)高中数学选择性必修第一册课件(18张PPT)
文档属性
| 名称 | 3.3.2直线与抛物线的位置关系-【新教材】人教A版(2019)高中数学选择性必修第一册课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 420.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-15 00:00:00 | ||
图片预览




文档简介
3.3.2 抛物线与直线的位置关系
复习回顾:
1、直线与圆、椭圆、双曲线
的位置关系有哪些?
2、怎样判断直线与
圆、椭圆、双曲线位置关系?
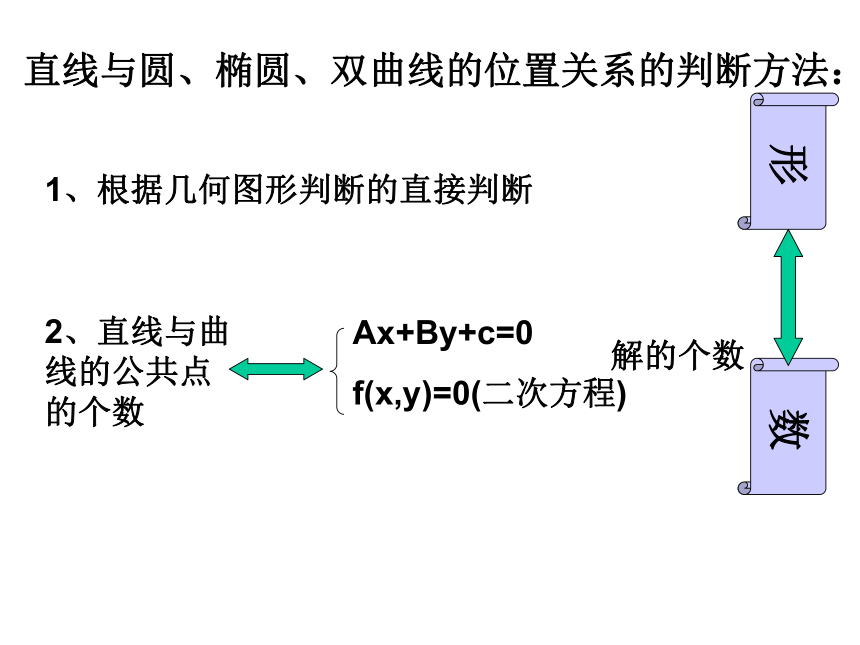
直线与圆、椭圆、双曲线的位置关系的判断方法:
1、根据几何图形判断的直接判断
2、直线与曲线的公共点的个数
Ax+By+c=0
f(x,y)=0(二次方程)
解的个数
形
数
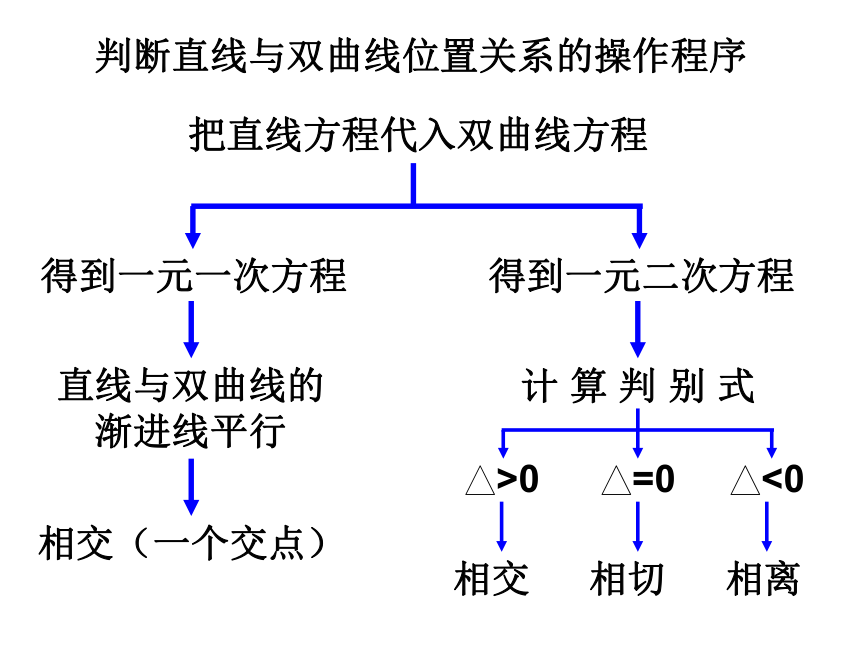
判断直线与双曲线位置关系的操作程序
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
F
x
y
问题:你能说出直线与抛物线位置关系吗?
二、讲授新课:
3
类型一:位置关系判断
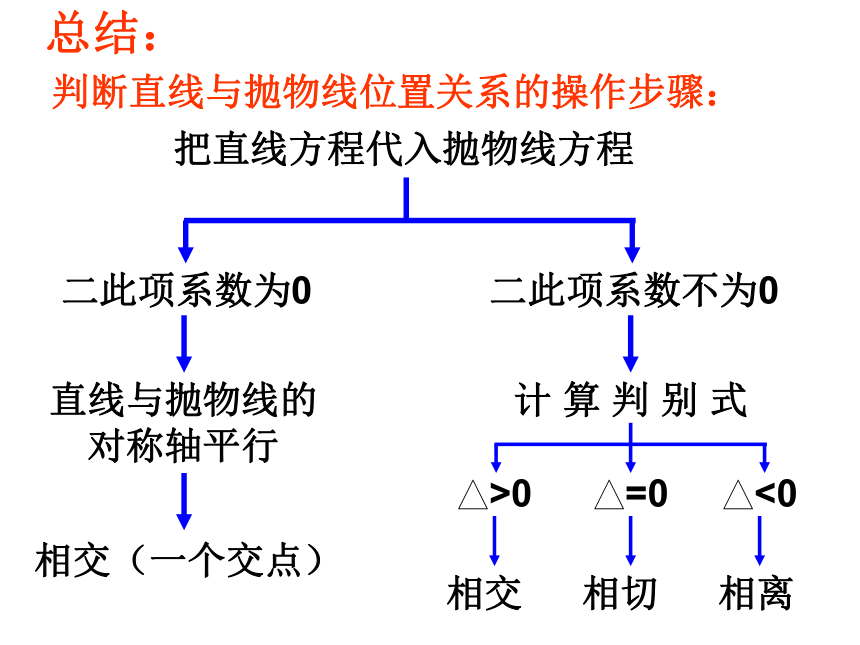
判断直线与抛物线位置关系的操作步骤:
把直线方程代入抛物线方程
二此项系数为0
二此项系数不为0
直线与抛物线的
对称轴平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
总结:
例2:求过定点(0,2),且与抛物线y2=4x相切的直线方程.
说明:(1)联立方程组,结合判别式求解
(2)注意斜率不存在的情形
例3、在抛物线y2=x上求一点,使它到直线L:x+y+4=0的距离最短,并求此距离.
.
F
例4、已知直线l:y=-x+1和抛物线
C:y2=4x,设直线与抛物线的交点为
A、B,求AB的长.
A
B
类型二:求弦长
8
.
F
类型三:定点问题
.
F
变式1: 若直线l与抛物线 =2px(p>0)交于A、B两点,
且OA⊥OB ,则_____ _____.
直线l过定点(2p,0)
x
y
O
y2=2px
A
B
l
P
变式2.已知直线l:x=2p与抛物线 =2px(p>0)交于A、B两点,
求证:OA⊥OB.
证明:由题意得,A(2p,2p),B(2p,-2p)
所以 =1, =-1
因此OA⊥OB
x
y
O
y2=2px
A
B
L:x=2p
C(2p,0)
变式: 若直线l过定点(2p,0)且与抛物线 =2px(p>0)交于A、B两点,求证:OA⊥OB.
x
y
O
y2=2px
A
B
l
P(2p,0)
练习1、已知过点M(2,0)的直线与抛物线C:y2=4x交于A、B两点,|AB|= ,求直线的方程.
练习2、已知抛物线的顶点在原点,以x轴为对称轴,经过焦点且斜率为-1的直线,被抛物线截得的弦长为8,求抛物线的方程
复习回顾:
1、直线与圆、椭圆、双曲线
的位置关系有哪些?
2、怎样判断直线与
圆、椭圆、双曲线位置关系?
直线与圆、椭圆、双曲线的位置关系的判断方法:
1、根据几何图形判断的直接判断
2、直线与曲线的公共点的个数
Ax+By+c=0
f(x,y)=0(二次方程)
解的个数
形
数
判断直线与双曲线位置关系的操作程序
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
F
x
y
问题:你能说出直线与抛物线位置关系吗?
二、讲授新课:
3
类型一:位置关系判断
判断直线与抛物线位置关系的操作步骤:
把直线方程代入抛物线方程
二此项系数为0
二此项系数不为0
直线与抛物线的
对称轴平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
总结:
例2:求过定点(0,2),且与抛物线y2=4x相切的直线方程.
说明:(1)联立方程组,结合判别式求解
(2)注意斜率不存在的情形
例3、在抛物线y2=x上求一点,使它到直线L:x+y+4=0的距离最短,并求此距离.
.
F
例4、已知直线l:y=-x+1和抛物线
C:y2=4x,设直线与抛物线的交点为
A、B,求AB的长.
A
B
类型二:求弦长
8
.
F
类型三:定点问题
.
F
变式1: 若直线l与抛物线 =2px(p>0)交于A、B两点,
且OA⊥OB ,则_____ _____.
直线l过定点(2p,0)
x
y
O
y2=2px
A
B
l
P
变式2.已知直线l:x=2p与抛物线 =2px(p>0)交于A、B两点,
求证:OA⊥OB.
证明:由题意得,A(2p,2p),B(2p,-2p)
所以 =1, =-1
因此OA⊥OB
x
y
O
y2=2px
A
B
L:x=2p
C(2p,0)
变式: 若直线l过定点(2p,0)且与抛物线 =2px(p>0)交于A、B两点,求证:OA⊥OB.
x
y
O
y2=2px
A
B
l
P(2p,0)
练习1、已知过点M(2,0)的直线与抛物线C:y2=4x交于A、B两点,|AB|= ,求直线的方程.
练习2、已知抛物线的顶点在原点,以x轴为对称轴,经过焦点且斜率为-1的直线,被抛物线截得的弦长为8,求抛物线的方程
