19[1].2.3_正方形(1)
文档属性
| 名称 | 19[1].2.3_正方形(1) |  | |
| 格式 | zip | ||
| 文件大小 | 631.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-09 22:49:38 | ||
图片预览




文档简介
(共34张PPT)
19.2.3 正方形
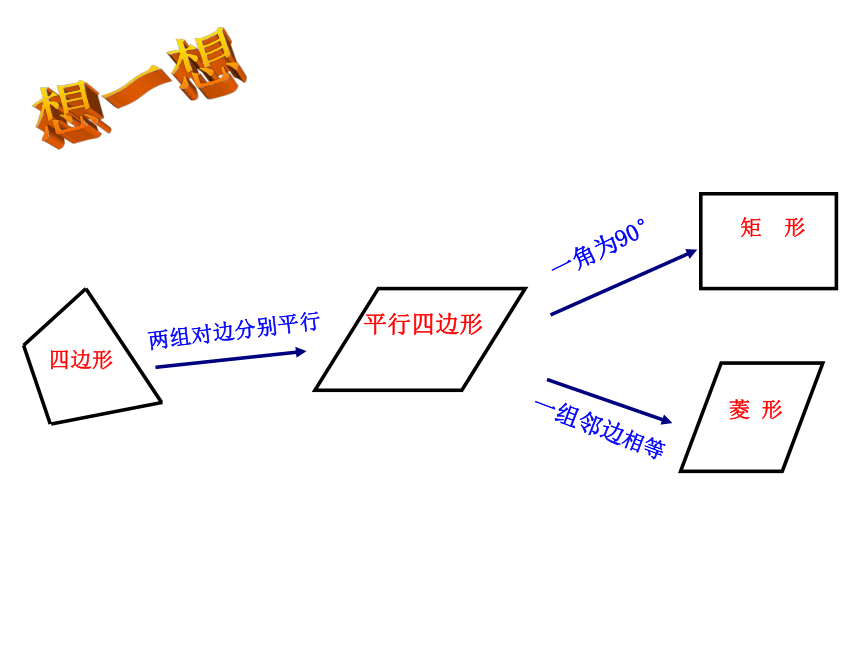
四边形
两组对边分别平行
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
操 作
⒈怎样用一张矩形的纸片折出一个正方形?
⒉怎样将一个菱形的木框变成一个正方形的木框?
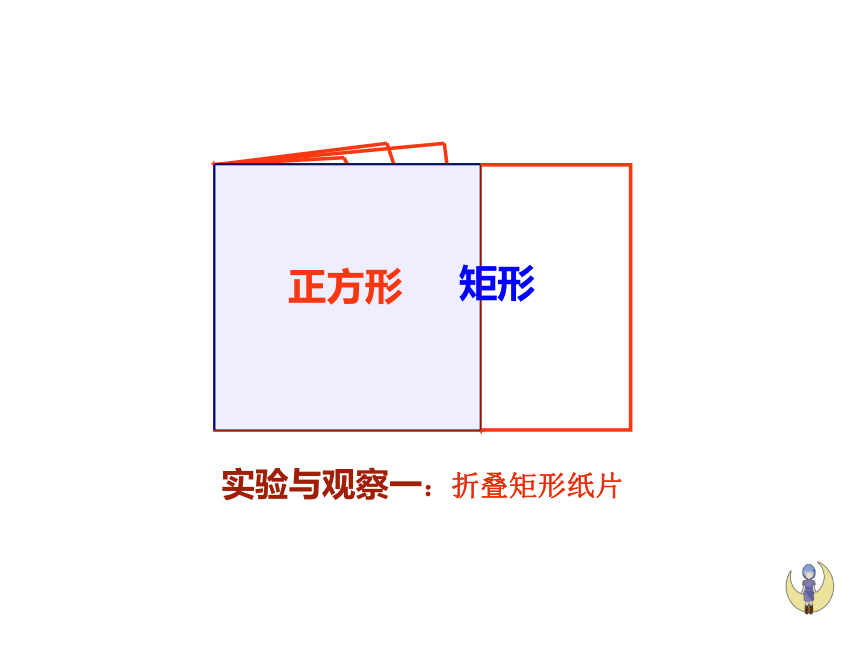
正方形
矩形
实验与观察一:折叠矩形纸片
矩 形
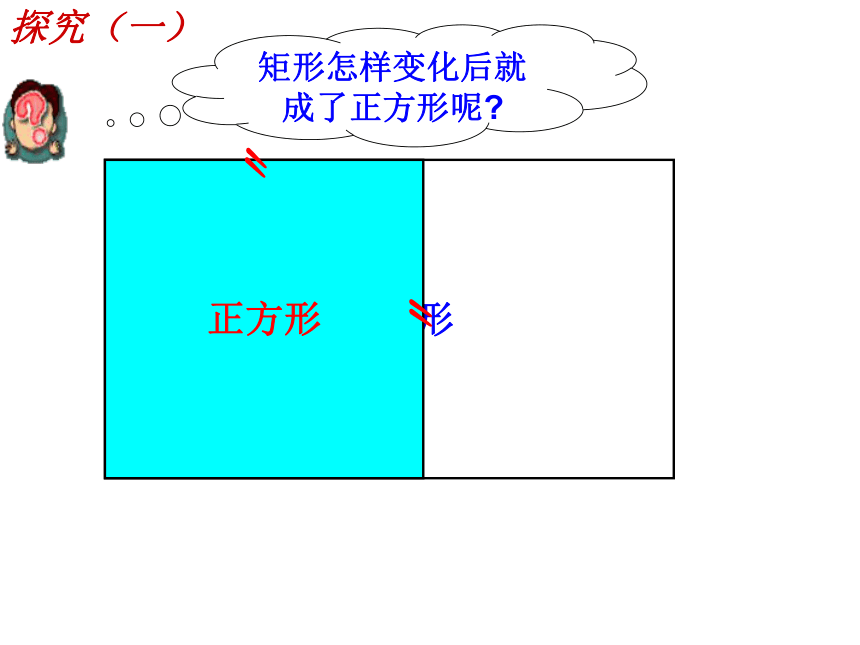
正方形
〃
〃
矩形怎样变化后就成了正方形呢
探究(一)
菱形
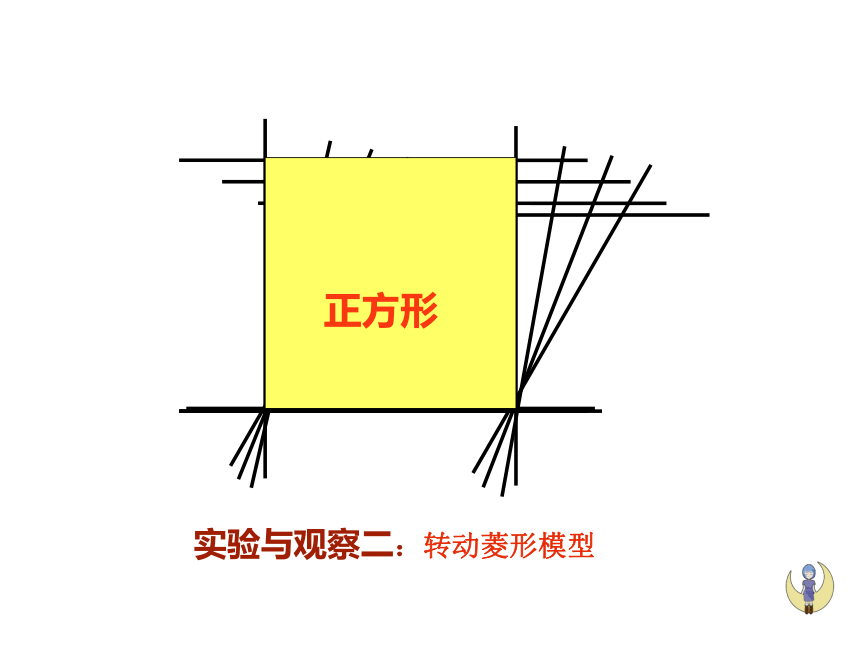
实验与观察二:转动菱形模型
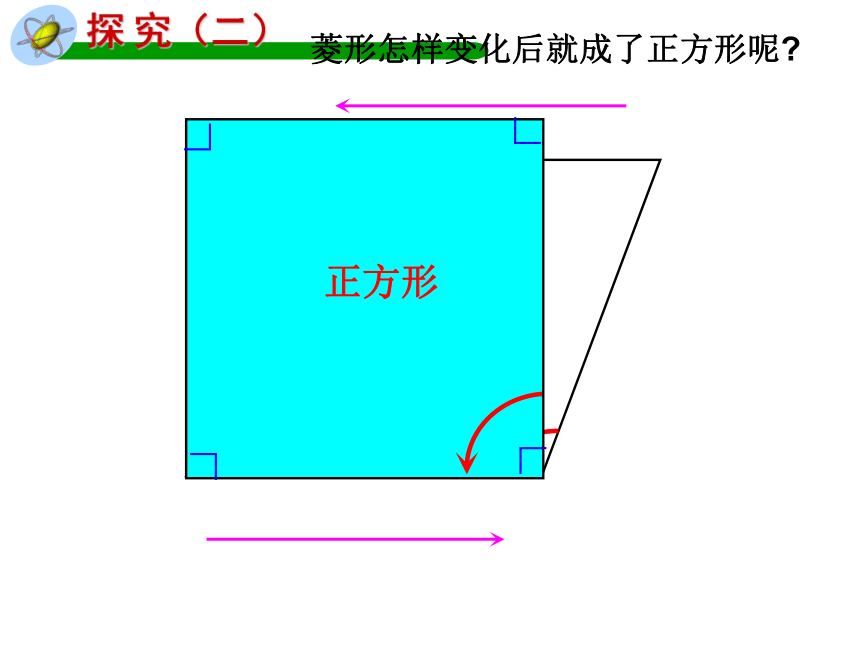
正方形
菱 形
∟
∟
∟
∟
正方形
探 究(二)
菱形怎样变化后就成了正方形呢
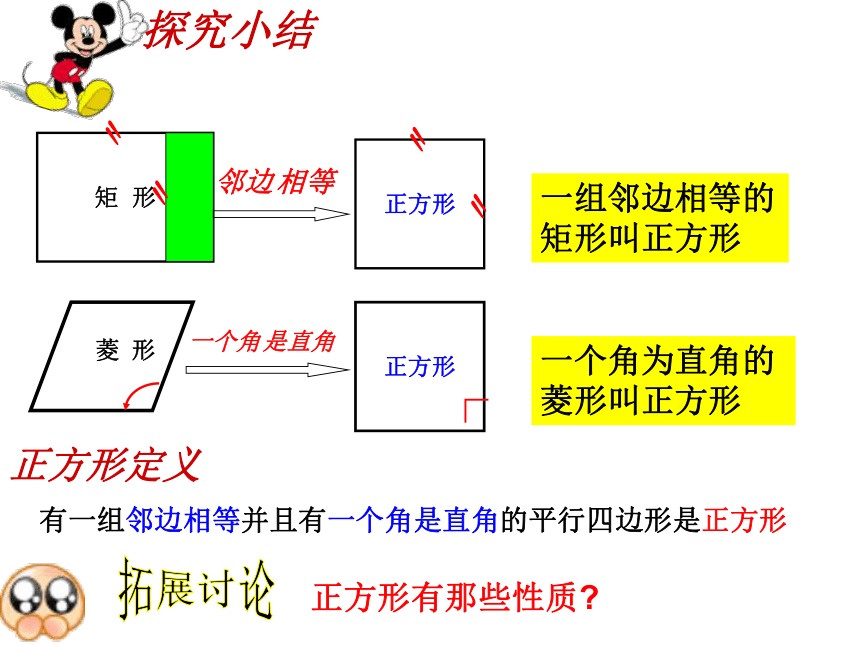
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
一组邻边相等的矩形叫正方形
菱 形
一个角
是直角
正方形
∟
一个角为直角的菱形叫正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
正方形有那些性质
讨 论
㈠正方形的边、角、对角线各具有什么性质?
边:对边平行,4条边都相等.
角:4个角都相等,都等于90°.
对角线:相等、垂直且互相平分,每一条对角线平分一组对角.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
正方形的性质=
例
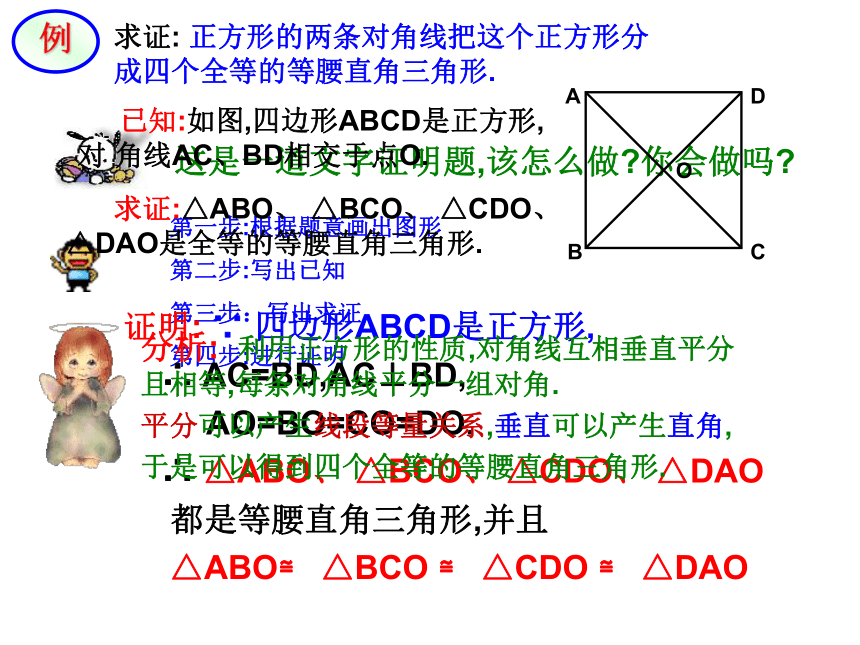
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO
都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析: 利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.
平分可以产生线段等量关系,垂直可以产生直角,
于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
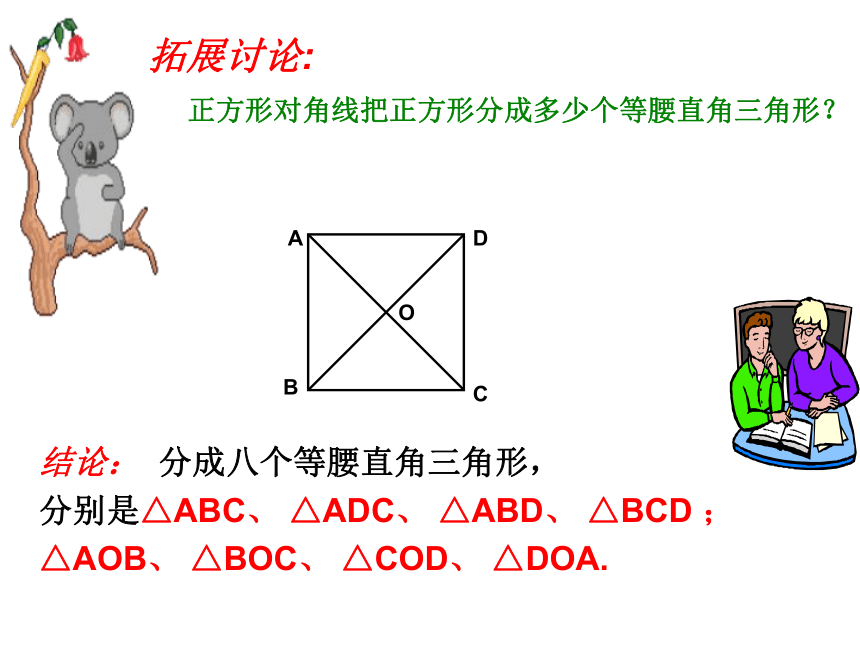
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论: 分成八个等腰直角三角形,
分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
讨 论
㈡具备什么条件的平行四边形是正方形?
⒈先说明它是矩形,再说明这个矩形有一组邻边相等.
⒉先说明它是菱形,再说明这个菱形有一个角是直角.
矩形
菱形
正方形
已知:平行四边形ABCD的对角线AC、BD交于点O,从下列条件中取出哪些条件后,可使平行四边形ABCD成为正方形。
(1)AB=AD;
(2)AC=BD;
(3)∠BAD=900;
(4)AC⊥BD。
A
B
C
D
O
合作探究
矩形
菱形
(2)
(3)
(1)
(4)
平行四边形
正方形
(1)AB=AD; (2)AC=BD;
(3)∠BAD=900; (4)AC⊥BD。
A
B
C
D
O
D
O
A
B
C
提示:有一组邻边相等的矩形是正方形
A
B
D
C
E
〃
〃
∟
F
正方形
裁
P101, 练习: 1、2 、3.
A
D
C
B
E
∟
∟
提示:寻找直角三角形,
运用直角三角形求边长和对角线.
P101, 练习: 1、2 、3.
面积=800m2
对角线AC=40m
P101, 练习: 1、2 、3.
√
√
√
√
知识拓展: 正方形、菱形、矩形、平行四边形四者之间有什么关系?与同学讨论后填写下表:
边 角 对 角 线 对 称 性
平 行
四边形
矩 形
菱 形
正方形
几种特殊四边形的性质
对边平行
且相等
对边平行 且相等
对边平行,四边都相等
对边平行,
四条边
都相等
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
对角线互相垂直平分且相等,每条对角线平分一组对角
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
平行四边形
矩形
菱形
正
方
形
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
性 质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
例题解析
1.已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
2.已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
例题解析
根据图形所具有的性质,
在下表相应的空格中打 ”√”
平行四边形 矩形 菱形 正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
1.平行四边形
有一组邻边相等
有一个角是直角
常
见
说
明
方
法
例题赏析
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
例题赏析
⒊在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P.
⑴求证:DQ=CP;
⑵OP与OQ有何关系?试证明你的结论.
一展身手
在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:
⑴CE=BG;
⑵EG=2AM.
H
M
E
D
F
G
B
C
A
求证:矩形的四个角的平分线所围成的四边形是正方形.
教学反思
▲正方形有哪些性质?如何判别一个平行四边形是正方形?
★从角上来谈;
●从边上来谈;
▲从对角线上来谈;
小结与复习
19.2.3 正方形
四边形
两组对边分别平行
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
操 作
⒈怎样用一张矩形的纸片折出一个正方形?
⒉怎样将一个菱形的木框变成一个正方形的木框?
正方形
矩形
实验与观察一:折叠矩形纸片
矩 形
正方形
〃
〃
矩形怎样变化后就成了正方形呢
探究(一)
菱形
实验与观察二:转动菱形模型
正方形
菱 形
∟
∟
∟
∟
正方形
探 究(二)
菱形怎样变化后就成了正方形呢
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
一组邻边相等的矩形叫正方形
菱 形
一个角
是直角
正方形
∟
一个角为直角的菱形叫正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
正方形有那些性质
讨 论
㈠正方形的边、角、对角线各具有什么性质?
边:对边平行,4条边都相等.
角:4个角都相等,都等于90°.
对角线:相等、垂直且互相平分,每一条对角线平分一组对角.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
正方形的性质=
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO
都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析: 利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.
平分可以产生线段等量关系,垂直可以产生直角,
于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论: 分成八个等腰直角三角形,
分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
讨 论
㈡具备什么条件的平行四边形是正方形?
⒈先说明它是矩形,再说明这个矩形有一组邻边相等.
⒉先说明它是菱形,再说明这个菱形有一个角是直角.
矩形
菱形
正方形
已知:平行四边形ABCD的对角线AC、BD交于点O,从下列条件中取出哪些条件后,可使平行四边形ABCD成为正方形。
(1)AB=AD;
(2)AC=BD;
(3)∠BAD=900;
(4)AC⊥BD。
A
B
C
D
O
合作探究
矩形
菱形
(2)
(3)
(1)
(4)
平行四边形
正方形
(1)AB=AD; (2)AC=BD;
(3)∠BAD=900; (4)AC⊥BD。
A
B
C
D
O
D
O
A
B
C
提示:有一组邻边相等的矩形是正方形
A
B
D
C
E
〃
〃
∟
F
正方形
裁
P101, 练习: 1、2 、3.
A
D
C
B
E
∟
∟
提示:寻找直角三角形,
运用直角三角形求边长和对角线.
P101, 练习: 1、2 、3.
面积=800m2
对角线AC=40m
P101, 练习: 1、2 、3.
√
√
√
√
知识拓展: 正方形、菱形、矩形、平行四边形四者之间有什么关系?与同学讨论后填写下表:
边 角 对 角 线 对 称 性
平 行
四边形
矩 形
菱 形
正方形
几种特殊四边形的性质
对边平行
且相等
对边平行 且相等
对边平行,四边都相等
对边平行,
四条边
都相等
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
对角线互相垂直平分且相等,每条对角线平分一组对角
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
平行四边形
矩形
菱形
正
方
形
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
性 质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
例题解析
1.已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
2.已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
例题解析
根据图形所具有的性质,
在下表相应的空格中打 ”√”
平行四边形 矩形 菱形 正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
1.平行四边形
有一组邻边相等
有一个角是直角
常
见
说
明
方
法
例题赏析
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
例题赏析
⒊在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P.
⑴求证:DQ=CP;
⑵OP与OQ有何关系?试证明你的结论.
一展身手
在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:
⑴CE=BG;
⑵EG=2AM.
H
M
E
D
F
G
B
C
A
求证:矩形的四个角的平分线所围成的四边形是正方形.
教学反思
▲正方形有哪些性质?如何判别一个平行四边形是正方形?
★从角上来谈;
●从边上来谈;
▲从对角线上来谈;
小结与复习
