2.2.2对数函数及其性质 课件(共43张PPT)——2020-2021学年高一上学期人教A版数学必修一
文档属性
| 名称 | 2.2.2对数函数及其性质 课件(共43张PPT)——2020-2021学年高一上学期人教A版数学必修一 |  | |
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 08:43:42 | ||
图片预览







文档简介
(共43张PPT)
§2.2.2
对数函数及其性质
由前面的学习我们知道:如果有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,···
,1个这样的细胞分裂x次会得到多少个细胞?
如果知道了细胞的个数y,如何确定分裂的次数x呢?
由对数式与指数式的互化可知:
上式可以看作以y为自变量的函数表达式
对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即
这就是本节课要学习的:
定义:函数
,且
叫做对数函数,其中x是自变量,函数的定义域是(0,+∞)。
观察给出对数函数的特征:
,
对数函数
判断:以下函数是对数函数的是
(
)
1.
y=log2(3x-2)
2.
y=log(x-1)x
3.
y=log1/3x2
4.y=lnx
5.
4
二.对数函数的图象:
1.描点画图
的变量x,y的对应值对调即可得到
y=logax(a>0,a≠1)的变量对应值表如下.
注意只要把指数函数y=ax
(a>0,a≠1)
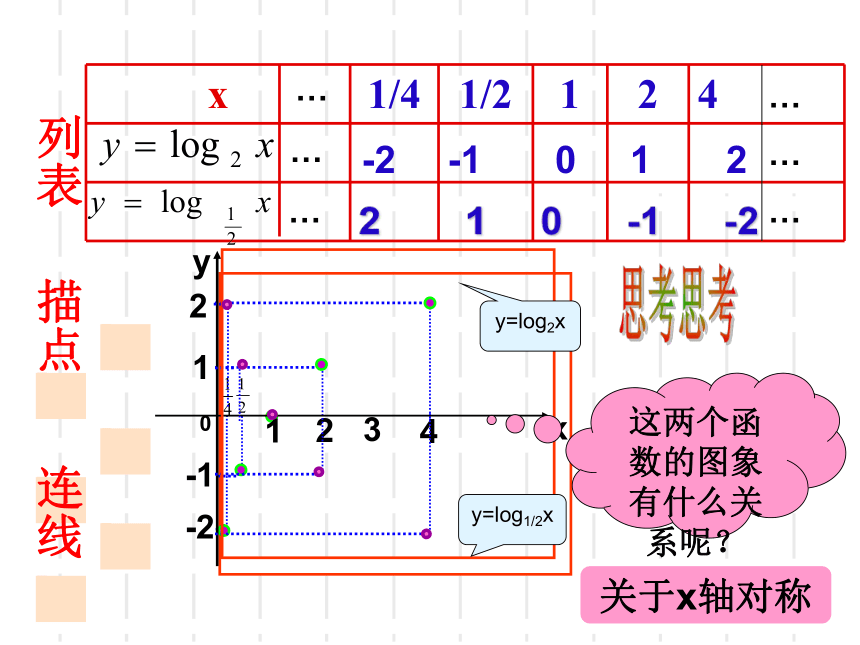
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2
1
0
-1
-2
-2
-1
0
1
2
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
y=log1/2x
y=log2x
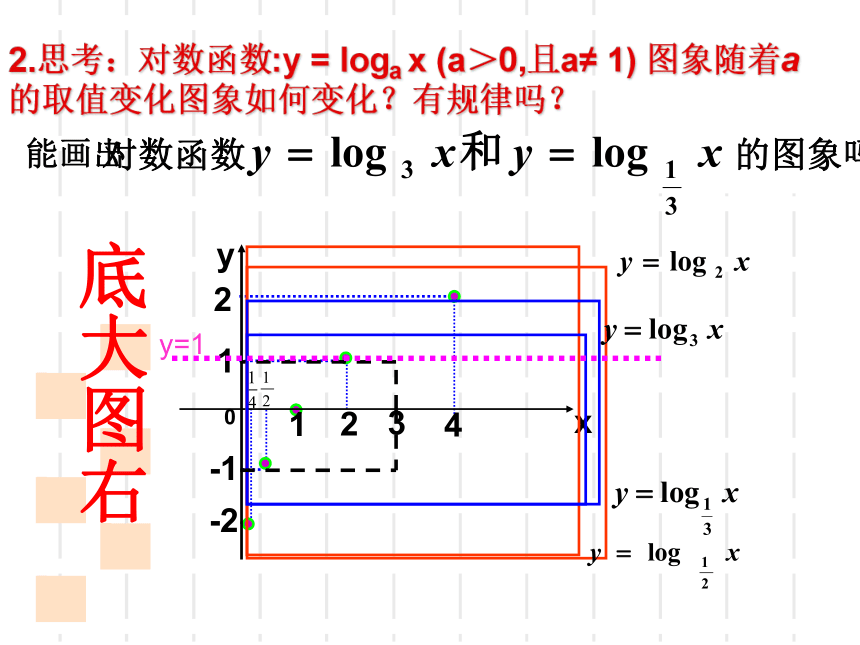
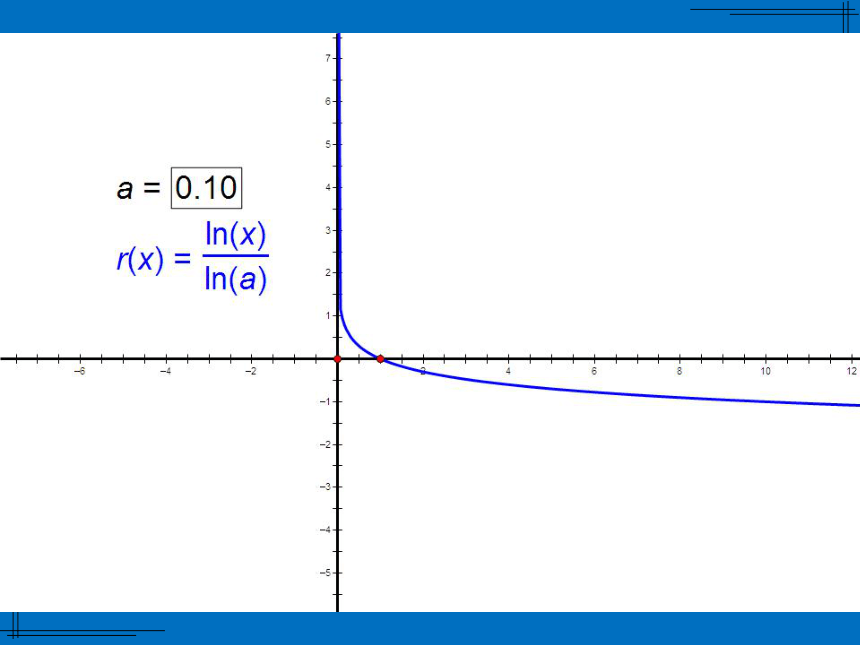
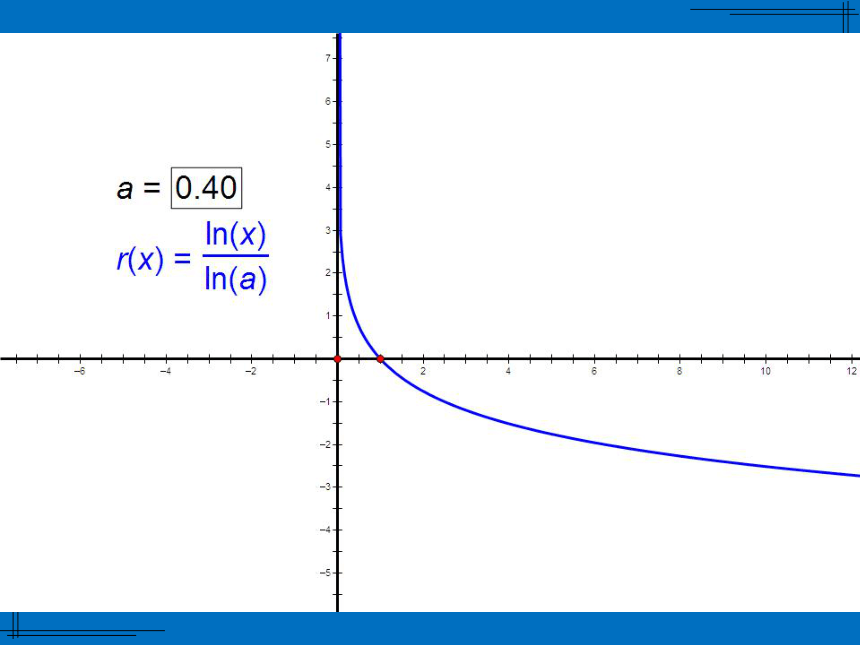
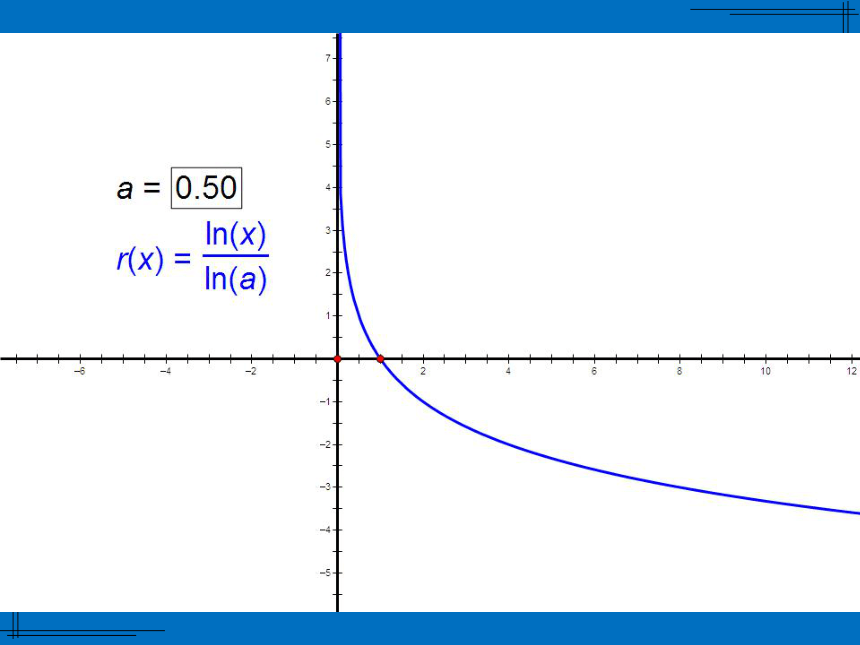
2.思考:对数函数:y
=
loga
x
(a>0,且a≠
1)
图象随着a
的取值变化图象如何变化?有规律吗?
对数函数
的图象吗?
能画出
2
1
-1
-2
1
2
4
0
y
x
3
底大图右
y=1
返回
再来一遍
问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
类比指数函数图象和性质的研究,研究对数函数的性质并填写如下表格:
3.对数函数的图象与性质:
函数
y
=
log
a
x
(
a>0
且
a≠1
)
底数
a
>
1
0
<
a
<
1
图象
定义域
奇偶性
值域
定点
单调性
函数值
符号
1
x
y
o
1
x
y
o
非奇非偶函数
非奇非偶函数
(
0
,
+
∞
)
R
(
1
,
0
)
即
x
=
1
时,y
=
0
在
(
0
,
+
∞
)
上是增函数
在
(
0
,
+
∞
)
上是减函数
当
x>1
时,y>0
当
0<x
<1
时,
y<0
当
x>1
时,y<0
当
0<x<1
时,y>0
例1:求下列函数的定义域:
(1)
y=logax2
(2)
y=loga(4-x)
解:
(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为
?-????
?
(0,+??
(2)因为
4-x>0,所以x<4,即函数y=loga(4-x)的定义域为
(-??4)
由例1再归纳定义域的求法:
1、对数的真数大于0,底数大于0且不等于1;
2、使式子符合实际背景;
3、对含有字母的式子要注意分类讨论。
4、5、6、…….
例2
比较下列各组数中两个值的大小:
⑴
log
23.4
,
log
28.5
⑵
log
0.31.8
,
log
0.32.7
⑶
log
a5.1
,
log
a5.9
(
a>0
,
a≠1
)
解 ⑴考察对数函数
y
=
log
2x,因为它的底数2>1
所以它在(0,+∞)上是增函数,于是
log
23.4<log
28.5
⑵考察对数函数
y
=
log
0.3
x,因为它的底数0.3,
即0<0.3<1,所以它在(0,+∞)上是减函数,于是log
0.31.8>log
0.32.7
对数函数的增减性决定于对数的底数是大于1还是小于1.而已知条件中并未指出底数a与1哪个大,因此需要对底数a进行讨论:
当a>1时,函数y=log
ax在(0,+∞)上是增函数,于是log
a5.1<log
a5.9
当0<a<1时,函数y=log
ax在(0,+∞)上是减函数,于是log
a5.1>log
a5.9
⑶
log
a5.1
,
log
a5.9
(
a>0
,
a≠1
)
注:例2是利用对数函数的增减性比较两个对数的大小的,对底数与1的大小关系未明确指出时,要分情况对底数进行讨论来比较两个对数的大小.
例3
比较下列各组中两个值的大小:
⑴.log
67
,
log
7
6
;
⑵.log
3π
,
log
2
0.8
.
解:
⑴ ∵ log67>log66=1
log76<log77=1
∴
log67>log76
⑵
∵ log3π>log31=0
log20.8<log21=0
∴
log3π>log20.8
注:例3是利用对数函数的增减性比较两个对数的大小.
当不能直接进行比较时,可在两个对数中间插入一
个已知数(如1或0等),间接比较上述两个对数的大小.
小结
(1)本节要求掌握对数函数的概念、图象和性质.
(2)在理解对数函数的定义的基础上,掌握对数函数的图象和性质的应用是本小节的重点.
作业:P74
习题2.2
A组
第7、8题
二、反函数的概念
指数函数
是
对数函数
的反函数。
对数函数与指数函数的图象
由于对数函数
与指数函数
互为反函数,
所以
的图象与
的图象关于直线
对称。
小结:
1.指数函数与对数函数的关系.
2.反函数的定义和图象的特点.
练习:
2.已知
是R上的奇
函数,(1)求a的值;(2)求f(x)的反函数;
1
§2.2.2
对数函数及其性质
由前面的学习我们知道:如果有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,···
,1个这样的细胞分裂x次会得到多少个细胞?
如果知道了细胞的个数y,如何确定分裂的次数x呢?
由对数式与指数式的互化可知:
上式可以看作以y为自变量的函数表达式
对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即
这就是本节课要学习的:
定义:函数
,且
叫做对数函数,其中x是自变量,函数的定义域是(0,+∞)。
观察给出对数函数的特征:
,
对数函数
判断:以下函数是对数函数的是
(
)
1.
y=log2(3x-2)
2.
y=log(x-1)x
3.
y=log1/3x2
4.y=lnx
5.
4
二.对数函数的图象:
1.描点画图
的变量x,y的对应值对调即可得到
y=logax(a>0,a≠1)的变量对应值表如下.
注意只要把指数函数y=ax
(a>0,a≠1)
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2
1
0
-1
-2
-2
-1
0
1
2
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
y=log1/2x
y=log2x
2.思考:对数函数:y
=
loga
x
(a>0,且a≠
1)
图象随着a
的取值变化图象如何变化?有规律吗?
对数函数
的图象吗?
能画出
2
1
-1
-2
1
2
4
0
y
x
3
底大图右
y=1
返回
再来一遍
问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
类比指数函数图象和性质的研究,研究对数函数的性质并填写如下表格:
3.对数函数的图象与性质:
函数
y
=
log
a
x
(
a>0
且
a≠1
)
底数
a
>
1
0
<
a
<
1
图象
定义域
奇偶性
值域
定点
单调性
函数值
符号
1
x
y
o
1
x
y
o
非奇非偶函数
非奇非偶函数
(
0
,
+
∞
)
R
(
1
,
0
)
即
x
=
1
时,y
=
0
在
(
0
,
+
∞
)
上是增函数
在
(
0
,
+
∞
)
上是减函数
当
x>1
时,y>0
当
0<x
<1
时,
y<0
当
x>1
时,y<0
当
0<x<1
时,y>0
例1:求下列函数的定义域:
(1)
y=logax2
(2)
y=loga(4-x)
解:
(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为
?-????
?
(0,+??
(2)因为
4-x>0,所以x<4,即函数y=loga(4-x)的定义域为
(-??4)
由例1再归纳定义域的求法:
1、对数的真数大于0,底数大于0且不等于1;
2、使式子符合实际背景;
3、对含有字母的式子要注意分类讨论。
4、5、6、…….
例2
比较下列各组数中两个值的大小:
⑴
log
23.4
,
log
28.5
⑵
log
0.31.8
,
log
0.32.7
⑶
log
a5.1
,
log
a5.9
(
a>0
,
a≠1
)
解 ⑴考察对数函数
y
=
log
2x,因为它的底数2>1
所以它在(0,+∞)上是增函数,于是
log
23.4<log
28.5
⑵考察对数函数
y
=
log
0.3
x,因为它的底数0.3,
即0<0.3<1,所以它在(0,+∞)上是减函数,于是log
0.31.8>log
0.32.7
对数函数的增减性决定于对数的底数是大于1还是小于1.而已知条件中并未指出底数a与1哪个大,因此需要对底数a进行讨论:
当a>1时,函数y=log
ax在(0,+∞)上是增函数,于是log
a5.1<log
a5.9
当0<a<1时,函数y=log
ax在(0,+∞)上是减函数,于是log
a5.1>log
a5.9
⑶
log
a5.1
,
log
a5.9
(
a>0
,
a≠1
)
注:例2是利用对数函数的增减性比较两个对数的大小的,对底数与1的大小关系未明确指出时,要分情况对底数进行讨论来比较两个对数的大小.
例3
比较下列各组中两个值的大小:
⑴.log
67
,
log
7
6
;
⑵.log
3π
,
log
2
0.8
.
解:
⑴ ∵ log67>log66=1
log76<log77=1
∴
log67>log76
⑵
∵ log3π>log31=0
log20.8<log21=0
∴
log3π>log20.8
注:例3是利用对数函数的增减性比较两个对数的大小.
当不能直接进行比较时,可在两个对数中间插入一
个已知数(如1或0等),间接比较上述两个对数的大小.
小结
(1)本节要求掌握对数函数的概念、图象和性质.
(2)在理解对数函数的定义的基础上,掌握对数函数的图象和性质的应用是本小节的重点.
作业:P74
习题2.2
A组
第7、8题
二、反函数的概念
指数函数
是
对数函数
的反函数。
对数函数与指数函数的图象
由于对数函数
与指数函数
互为反函数,
所以
的图象与
的图象关于直线
对称。
小结:
1.指数函数与对数函数的关系.
2.反函数的定义和图象的特点.
练习:
2.已知
是R上的奇
函数,(1)求a的值;(2)求f(x)的反函数;
1
