13.3实数(2)
图片预览







文档简介
(共21张PPT)
随堂练习
1、 的相反数是 ,绝对值是 .
2、绝对值等于 的数是 , 的平方 是 .
3、比较大小:-7
正实数的绝对值是 ;
0的绝对值是 ;
负实数的绝对值是 。
它本身
0
它的相反数
4、 的绝对值是 。
4
例1. [P84]
(1)分别写出 的相反数;
(2)指出 各是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值为 ,求这个数.
若a、b互为相反数,c、d互为倒数,则
1
练习3
P86: 1,2.
合作学习
总结有理数的运算律和运算法则
1.交换律 : 加法 a+b=b+a
乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)
3.分配律: a× (b+c)= a×b+ a×c
注:有理数的运算律和运算法则在实数范围内同样适用
实数的运算顺序
先算乘方和开方,再算乘除,最后算加减。如果遇到括号, 则先进行括号里的运算。
例2 计算:
(1) (2)
典型例题
解:
[P85]
(加法结合律)
(分配律)
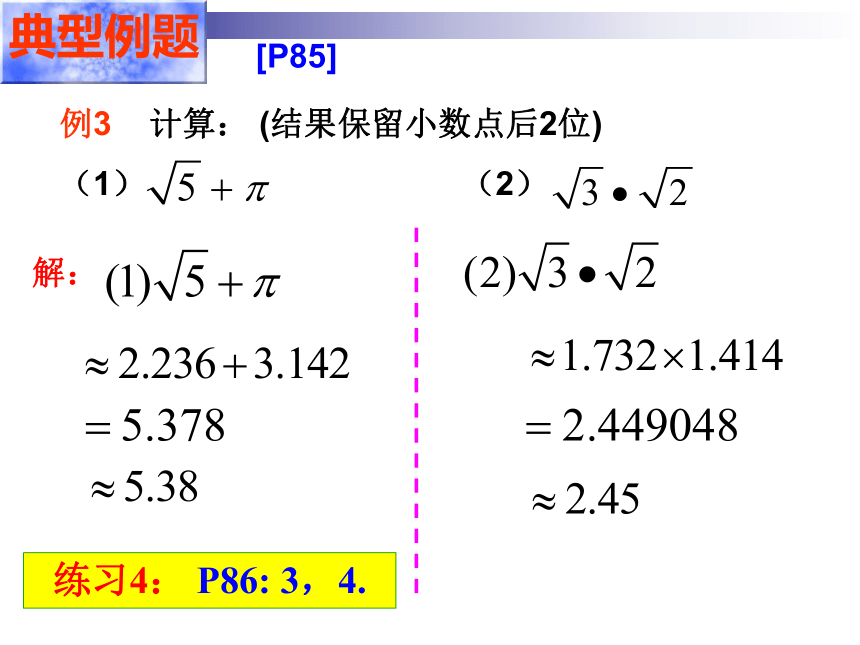
例3 计算: (结果保留小数点后2位)
(1) (2)
典型例题
解:
[P85]
练习4: P86: 3,4.
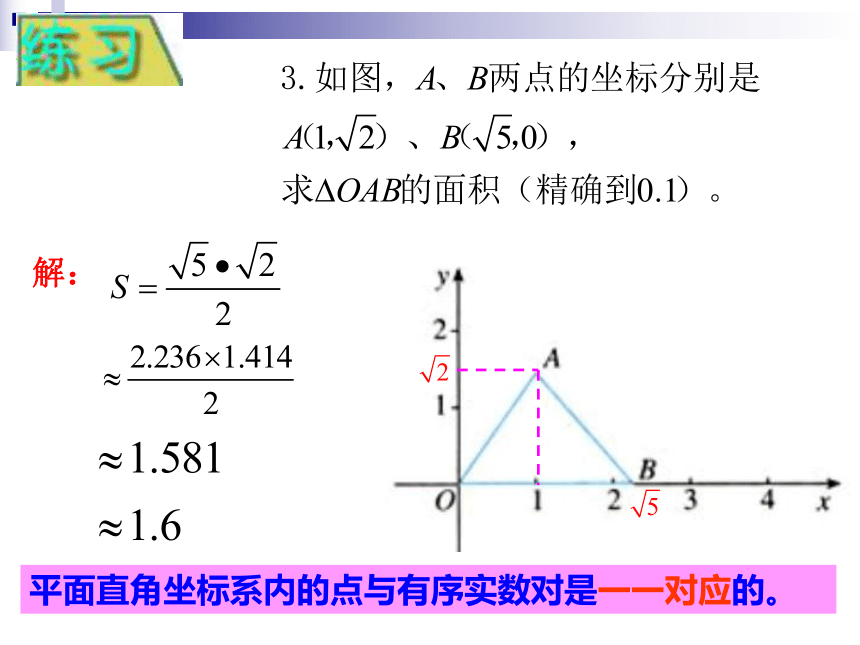
平面直角坐标系内的点与有序实数对是一一对应的。
解:
练习2: 填空:
(1) 的相反数是__________
(5) 绝对值是 _________
(2) 的倒数是____,
(3)| |=___________
(4)绝对值等于 的数是 _________ .
的立方是___.
典型例题
例4:计算
解:原式=
=18.94427191≈18.94
=
=
=
(结果保留2位小数)
随堂练习
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
8.数轴上的任何一点都可以表示实数。( )
×
×
×
随堂练习
二、填空
2、 的相反数是 ,绝对值是 .
3、绝对值等于 的数是 , 的平方 是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
5、在实数 中,
整数有
有理数有
无理数有
实数有
它本身
0
它的相反数
6.在实数范围内,下列判断正确的是( )
(A)若|x|=|y|,则x=y. (B)若x>y,则x2>y2.
(C)若|x|=( )2,则x=y. (D)若 ,则x=y
5.在数轴上一个点到原点的距离为 ,则这个数点
表示的数为( )
D
D
计算:
(1) (精确到0.001)
(2) (结果保留4个有效数字)
解:(1) = 0.748343301≈0.748
(2) =
=
=-2.464101615≈-2.464
计算:
(1) (精确到0.01)
(2) (结果保留3各有效数字)
(3) ( 精确到0.01)
例. 求下列各数的相反数、倒数、绝对值:
的相反数
的绝对值
计算:
(1) (结果保留3个有效数字)
(2) (精确到0.01)
(3) (结果保留4个有效数字)
通过今天的学习,
用你自己的话说说你的收获和体会
计算下面的式子:
与
与
你发现了什么?换几个数再试一试,是否有相同的规律?
探
究
活
动
随堂练习
1、 的相反数是 ,绝对值是 .
2、绝对值等于 的数是 , 的平方 是 .
3、比较大小:-7
正实数的绝对值是 ;
0的绝对值是 ;
负实数的绝对值是 。
它本身
0
它的相反数
4、 的绝对值是 。
4
例1. [P84]
(1)分别写出 的相反数;
(2)指出 各是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值为 ,求这个数.
若a、b互为相反数,c、d互为倒数,则
1
练习3
P86: 1,2.
合作学习
总结有理数的运算律和运算法则
1.交换律 : 加法 a+b=b+a
乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)
3.分配律: a× (b+c)= a×b+ a×c
注:有理数的运算律和运算法则在实数范围内同样适用
实数的运算顺序
先算乘方和开方,再算乘除,最后算加减。如果遇到括号, 则先进行括号里的运算。
例2 计算:
(1) (2)
典型例题
解:
[P85]
(加法结合律)
(分配律)
例3 计算: (结果保留小数点后2位)
(1) (2)
典型例题
解:
[P85]
练习4: P86: 3,4.
平面直角坐标系内的点与有序实数对是一一对应的。
解:
练习2: 填空:
(1) 的相反数是__________
(5) 绝对值是 _________
(2) 的倒数是____,
(3)| |=___________
(4)绝对值等于 的数是 _________ .
的立方是___.
典型例题
例4:计算
解:原式=
=18.94427191≈18.94
=
=
=
(结果保留2位小数)
随堂练习
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
8.数轴上的任何一点都可以表示实数。( )
×
×
×
随堂练习
二、填空
2、 的相反数是 ,绝对值是 .
3、绝对值等于 的数是 , 的平方 是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
5、在实数 中,
整数有
有理数有
无理数有
实数有
它本身
0
它的相反数
6.在实数范围内,下列判断正确的是( )
(A)若|x|=|y|,则x=y. (B)若x>y,则x2>y2.
(C)若|x|=( )2,则x=y. (D)若 ,则x=y
5.在数轴上一个点到原点的距离为 ,则这个数点
表示的数为( )
D
D
计算:
(1) (精确到0.001)
(2) (结果保留4个有效数字)
解:(1) = 0.748343301≈0.748
(2) =
=
=-2.464101615≈-2.464
计算:
(1) (精确到0.01)
(2) (结果保留3各有效数字)
(3) ( 精确到0.01)
例. 求下列各数的相反数、倒数、绝对值:
的相反数
的绝对值
计算:
(1) (结果保留3个有效数字)
(2) (精确到0.01)
(3) (结果保留4个有效数字)
通过今天的学习,
用你自己的话说说你的收获和体会
计算下面的式子:
与
与
你发现了什么?换几个数再试一试,是否有相同的规律?
探
究
活
动
