七年级数学三角形的内角
图片预览



文档简介
(共25张PPT)
我在来的路上不小心弄坏了一个三角形纸片,只知道剩下的两个角的度数分别是60°和40°,请问损坏的这个角为几度
A
B
C
演示
下一页
1
2
3
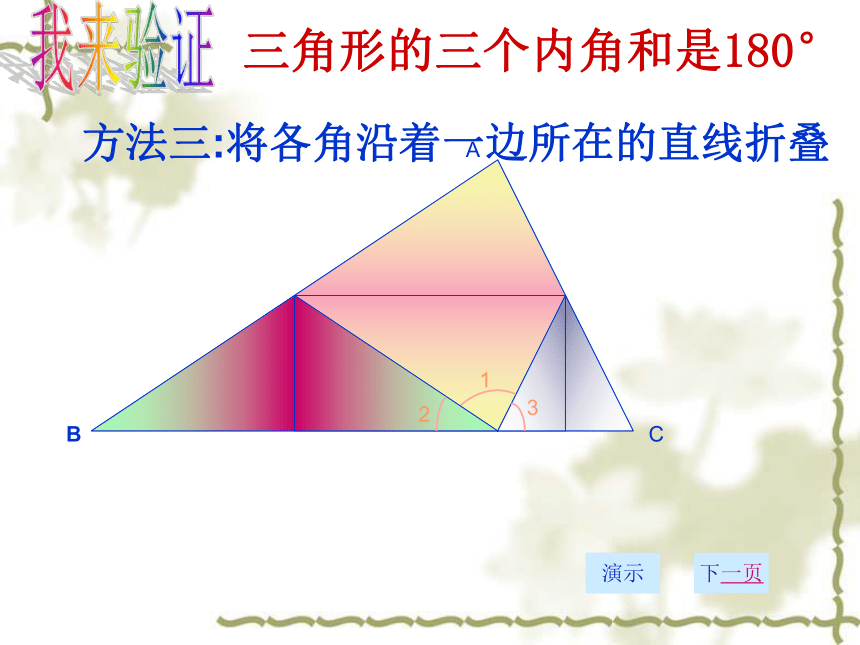
方法三:将各角沿着一边所在的直线折叠
三角形的三个内角和是180°
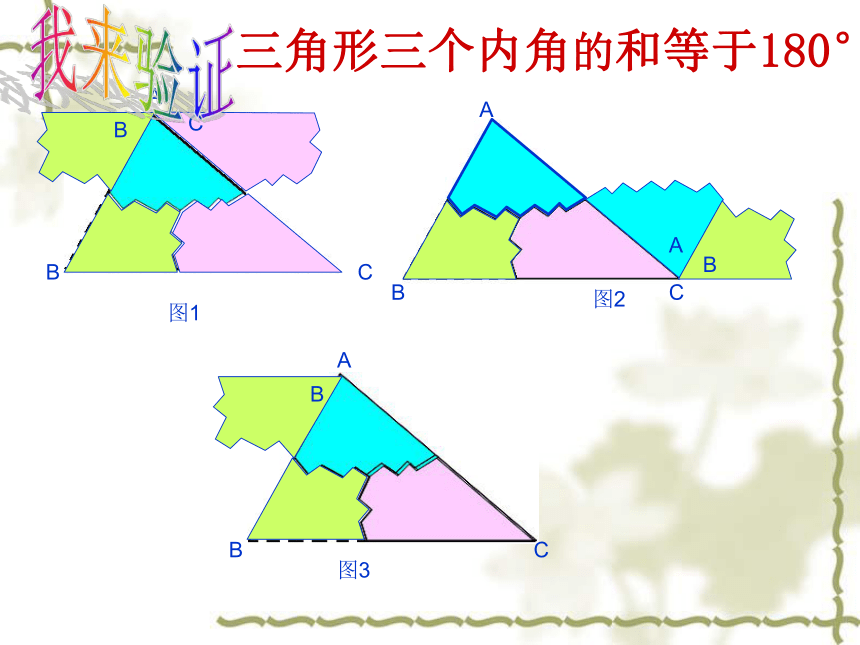
图1
图2
图3
A
B
C
C
B
A
A
B
B
C
C
B
A
B
三角形三个内角的和等于180°
三角形三个内角的和等于180°
命题:三角形的三个内角和是180°
你能验证这个命题吗?
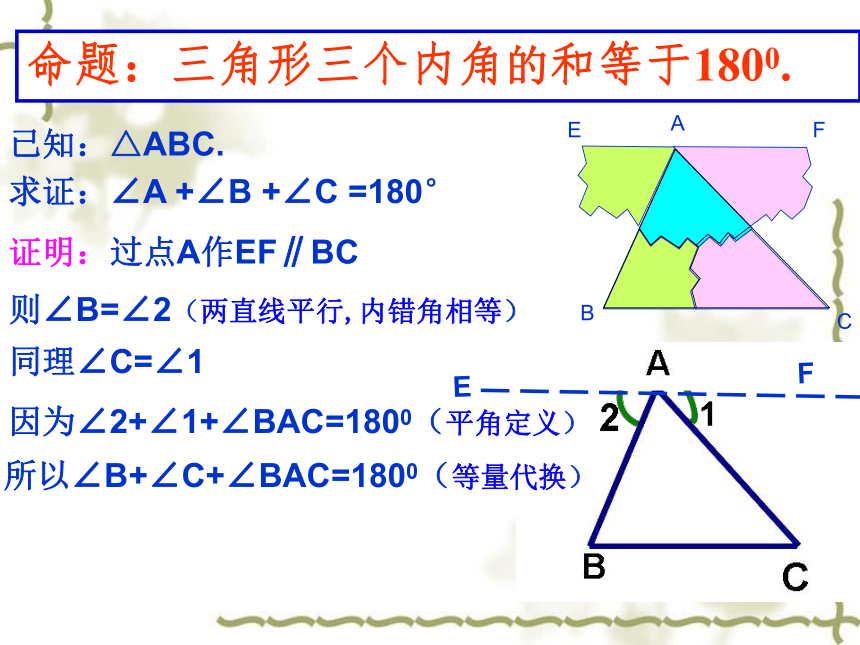
命题:三角形三个内角的和等于1800.
证明:过点A作EF∥BC
则∠B=∠2(两直线平行,内错角相等)
同理∠C=∠1
因为∠2+∠1+∠BAC=1800(平角定义)
所以∠B+∠C+∠BAC=1800(等量代换)
已知:△ABC.
A
B
C
E
F
求证:∠A +∠B +∠C =180°
E F
证明:
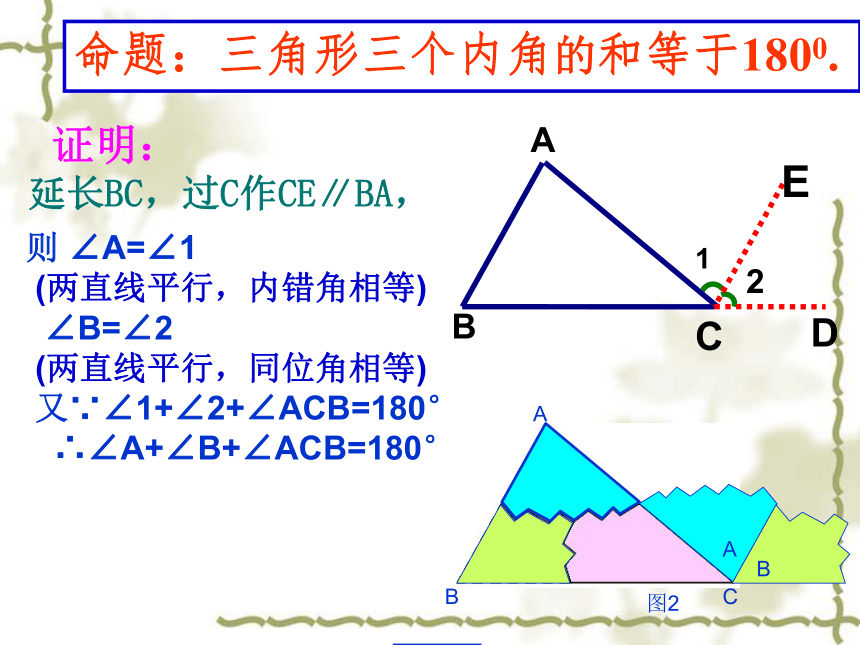
延长BC,过C作CE∥BA,
2
1
E
D
C
B
A
命题:三角形三个内角的和等于1800.
则 ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
图2
A
B
C
A
B
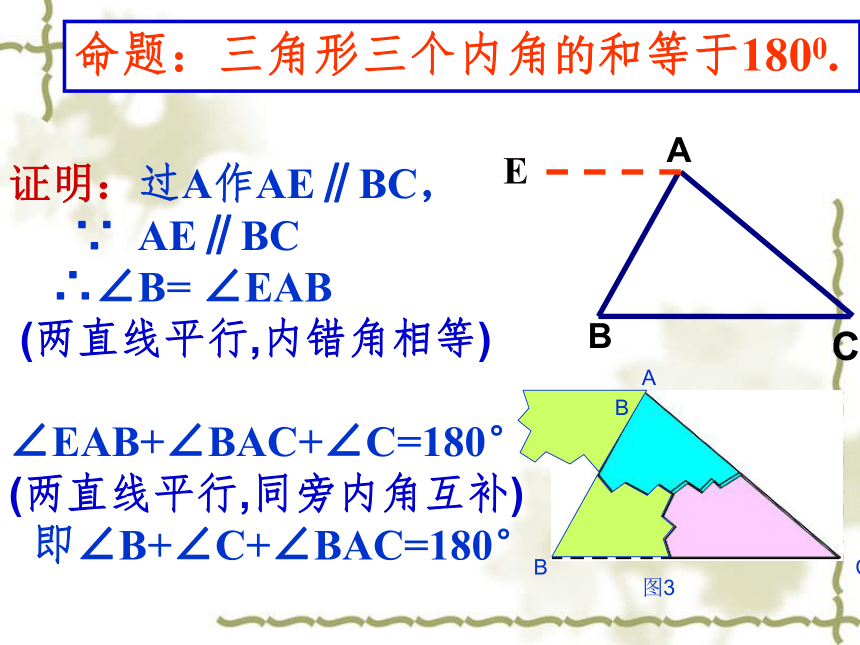
证明:过A作AE∥BC,
∵ AE∥BC
∴∠B= ∠EAB
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
即∠B+∠C+∠BAC=180°
命题:三角形三个内角的和等于1800.
C
B
A
E
图3
A
B
C
B
在这里,为了证明的需要,在原来的图形上自己加上的线叫做辅助线。在平面几何里,辅助线通常画成虚线。注意要说明所加辅助线的位置、名称和性质。
思路总结:
为了证明三角形三个内角的和为180°,通常应用转化思想。转化为:
平角或两直线平行,同旁内角互补
三角形三个内角的和等于180°
三角形内角和定理
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
n=
算一算
n
°
80
°
70
°
x
°
x
°
120
°
X=
y=
(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
A
B
C
D
E
北
北
例 C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
50°
80°
40°
30 °
?
例题导航:
在△ ABC中利用三角形内角和定理求 ∠ ACB,只要求出∠ 和∠ 即可。
已知解析:
C岛在A岛的北偏东50°方向,是指∠ = 50°
B岛在A岛的北偏东80°方向,是指∠ = 80°
C岛在B岛的北偏西40°方向。是指∠ = 40°
思考: ∠ABE = .
B
E
北
例 C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
解: ∠CAB=∠BAD -∠ CAD=80 ° -50 °=30 °
由AD∥BE,可得∠ BAD+∠ABE = 180 °
所以∠ ABE=180 °-∠ BAD= 180 °- 80 °= 100 °
∠ ABC= ∠ ABE -∠ EBC= 100 °- 40 °= 60 °
在△ ABC中, ∠ ACB= 180 °-∠ ABC -∠CAB
= 180 °- 60 °- 30 °= 90 °
答:从C岛看A、B两岛的视角∠ACB是90 ° 。
40°
A
C
D
北
50°
80°
30 °
?
C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
思考题
A
B
C
D
北
E
北
50°
40°
你还能想出其他的办法吗?
F
1
2
D
C
E
北
A
50°
∟
B
40 °
北
M
N
在△AMC中 ∠AMC=90°, ∠MAC= 50° ∴∠1=180 °- 90°- 50° = 40° ∵ AD∥BE ∴ ∠AMC+ ∠BNC =180 ° ∴ ∠BNC =90° 同理得 ∠2 = 50° ∴ ∠ACB = 180 ° - ∠1 - ∠2=180 °- 40°- 50° = 90°
解:过点C画MN⊥AD分别交AD、BE于点M、N
1
2
解法三
1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一 样的玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去
(C)带③去 (D)带①和②去
C
1、在 ABC中, A=50°, B= C,则 C=——
2、在△ABC中,∠A=42°,∠B=96°,则 ∠C= °
1、若∠A∶∠B∶∠C=1∶2∶3,则∠A= ∠B= ∠C=——
当堂达标:
1、一个三角形最多有 个直角,最多有 个钝角。
2在 ABC中, A=50°, B= C,则 C=
3在△ABC中,∠A=42°,∠B=96°,则 ∠C= °
4若∠A∶∠B∶∠C=2∶3∶4,则∠A= ∠B= ∠C= ;
5.△A B C中,∠A =∠B +∠C,判断△A B C是什么三角形状?
本节课里你学到了什么???
1、三角形内角和的定理:三角形三个内角的和等于180 °
2、通过思考、去探究、去总结三角形内角和的定理,并且发现要证明三角形三个内角的和等于180 °需
转化为:平角或两直线平行同旁内角和等于180°。
3、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角。
4、体会一题多解
我在来的路上不小心弄坏了一个三角形纸片,只知道剩下的两个角的度数分别是60°和40°,请问损坏的这个角为几度
A
B
C
演示
下一页
1
2
3
方法三:将各角沿着一边所在的直线折叠
三角形的三个内角和是180°
图1
图2
图3
A
B
C
C
B
A
A
B
B
C
C
B
A
B
三角形三个内角的和等于180°
三角形三个内角的和等于180°
命题:三角形的三个内角和是180°
你能验证这个命题吗?
命题:三角形三个内角的和等于1800.
证明:过点A作EF∥BC
则∠B=∠2(两直线平行,内错角相等)
同理∠C=∠1
因为∠2+∠1+∠BAC=1800(平角定义)
所以∠B+∠C+∠BAC=1800(等量代换)
已知:△ABC.
A
B
C
E
F
求证:∠A +∠B +∠C =180°
E F
证明:
延长BC,过C作CE∥BA,
2
1
E
D
C
B
A
命题:三角形三个内角的和等于1800.
则 ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
图2
A
B
C
A
B
证明:过A作AE∥BC,
∵ AE∥BC
∴∠B= ∠EAB
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
即∠B+∠C+∠BAC=180°
命题:三角形三个内角的和等于1800.
C
B
A
E
图3
A
B
C
B
在这里,为了证明的需要,在原来的图形上自己加上的线叫做辅助线。在平面几何里,辅助线通常画成虚线。注意要说明所加辅助线的位置、名称和性质。
思路总结:
为了证明三角形三个内角的和为180°,通常应用转化思想。转化为:
平角或两直线平行,同旁内角互补
三角形三个内角的和等于180°
三角形内角和定理
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
n=
算一算
n
°
80
°
70
°
x
°
x
°
120
°
X=
y=
(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
A
B
C
D
E
北
北
例 C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
50°
80°
40°
30 °
?
例题导航:
在△ ABC中利用三角形内角和定理求 ∠ ACB,只要求出∠ 和∠ 即可。
已知解析:
C岛在A岛的北偏东50°方向,是指∠ = 50°
B岛在A岛的北偏东80°方向,是指∠ = 80°
C岛在B岛的北偏西40°方向。是指∠ = 40°
思考: ∠ABE = .
B
E
北
例 C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
解: ∠CAB=∠BAD -∠ CAD=80 ° -50 °=30 °
由AD∥BE,可得∠ BAD+∠ABE = 180 °
所以∠ ABE=180 °-∠ BAD= 180 °- 80 °= 100 °
∠ ABC= ∠ ABE -∠ EBC= 100 °- 40 °= 60 °
在△ ABC中, ∠ ACB= 180 °-∠ ABC -∠CAB
= 180 °- 60 °- 30 °= 90 °
答:从C岛看A、B两岛的视角∠ACB是90 ° 。
40°
A
C
D
北
50°
80°
30 °
?
C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
思考题
A
B
C
D
北
E
北
50°
40°
你还能想出其他的办法吗?
F
1
2
D
C
E
北
A
50°
∟
B
40 °
北
M
N
在△AMC中 ∠AMC=90°, ∠MAC= 50° ∴∠1=180 °- 90°- 50° = 40° ∵ AD∥BE ∴ ∠AMC+ ∠BNC =180 ° ∴ ∠BNC =90° 同理得 ∠2 = 50° ∴ ∠ACB = 180 ° - ∠1 - ∠2=180 °- 40°- 50° = 90°
解:过点C画MN⊥AD分别交AD、BE于点M、N
1
2
解法三
1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一 样的玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去
(C)带③去 (D)带①和②去
C
1、在 ABC中, A=50°, B= C,则 C=——
2、在△ABC中,∠A=42°,∠B=96°,则 ∠C= °
1、若∠A∶∠B∶∠C=1∶2∶3,则∠A= ∠B= ∠C=——
当堂达标:
1、一个三角形最多有 个直角,最多有 个钝角。
2在 ABC中, A=50°, B= C,则 C=
3在△ABC中,∠A=42°,∠B=96°,则 ∠C= °
4若∠A∶∠B∶∠C=2∶3∶4,则∠A= ∠B= ∠C= ;
5.△A B C中,∠A =∠B +∠C,判断△A B C是什么三角形状?
本节课里你学到了什么???
1、三角形内角和的定理:三角形三个内角的和等于180 °
2、通过思考、去探究、去总结三角形内角和的定理,并且发现要证明三角形三个内角的和等于180 °需
转化为:平角或两直线平行同旁内角和等于180°。
3、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角。
4、体会一题多解
