1.1.1空间向量及其线性运算-【新教材】人教A版(2019)高中数学选择性必修第一册课件(共23张PPT)
文档属性
| 名称 | 1.1.1空间向量及其线性运算-【新教材】人教A版(2019)高中数学选择性必修第一册课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 919.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 13:53:35 | ||
图片预览







文档简介
第1课时 空间向量的线性运算
重难点:1.会用图形说明空间向量加法、减法、数 乘向量及它们的运算律.
2.能运用空间向量的运算意义及运算律解 决简单的立体几何问题.
与平面向量一样:
一、空间向量的概念
(1)向量:在空间中,具_________和______的量.
(2)向量a的长度或模:表示向量a的有向线段的长度,记作|a|.
(3)零向量:长度为______的向量。(手写记作 )
单位向量:长度为_______的向量。
(4)相等向量:在空间,方向相同且模相等的向量。
(5)相反向量:长度_______方向________的向量。
(6)共线向量或平行向量:如果表示若干空间向量的有向线段所在的直线互相平行或重合。
规定:零向量与任意向量共线.
大小
方向
做一做1、正方体ABCD - A'B'C'D'中与向量相等的向量有_____
1
相等
相反
0
3
已知空间向量 ,以任意点O为起点 ,作向量 ,我们就可以把他们平移到同一平面 ,这样任意的两个空间向量的运算就可以转化为平面向量运算。由此,我们把平面向量的运算推广到空间,定义空间向量的加减法以及数乘运算:
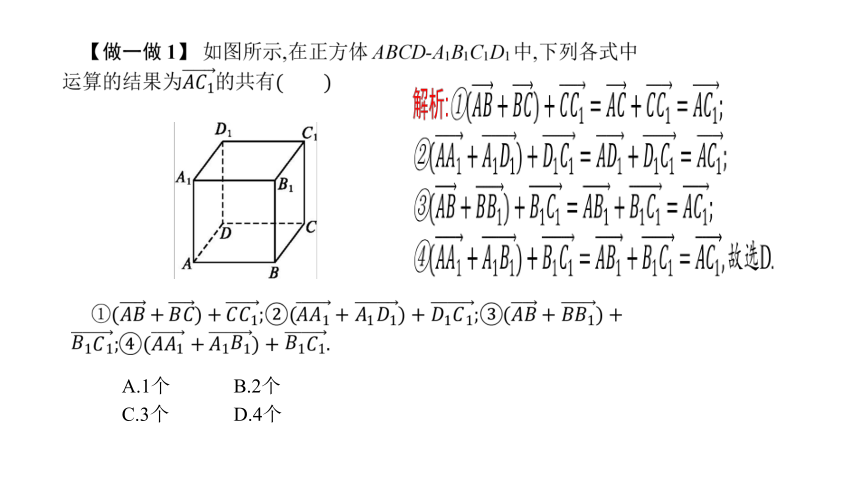
A.1个 B.2个
C.3个 D.4个
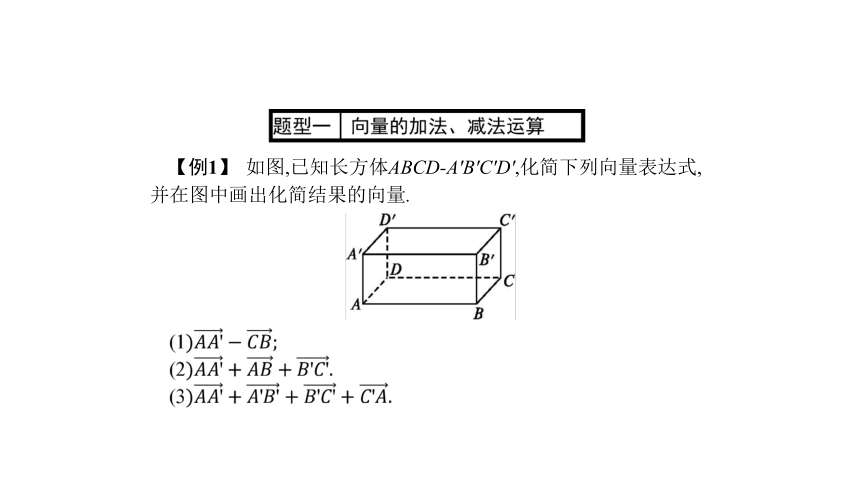
【例1】 如图,已知长方体ABCD-A'B'C'D',化简下列向量表达式,并在图中画出化简结果的向量.
反思运用法则进行向量的线性运算时要注意关键的要素:
(1)向量加法的三角形法则:“首尾相接,指向终点”;
(2)向量减法的三角形法则:“起点重合,指向被减向量”;
(3)平行四边形法则:“起点重合”;
(4)多边形法则:“首尾相接,指向终点”.
运算律
与平面向量一样,空间向量的线性运算满足以下运算律((λ∈R,μ∈R):
(1)结合律 (a+b)+c=a+(b+c);
(2)交换律 a+b=b+a.
(3)分配律 λ(a+b)=λa+λb,(λ+μ)a=λa+μa(λ∈R,μ∈R);
说明:空间向量的加法、减法运算满足平行四边形法则或三角形法则,并且空间向量的加法满足交换律和结合律.
答案:0
反思数乘向量的运算一般是结合所给几何体,联系数乘向量的几何意义转化为一个新的向量.若同时涉及几个数乘向量,则还要注意数乘向量运算律的运用.
共线向量定理: 空间两个向量a与b(b≠0)共线的充要条件是存在实数λ,使得a=λb.
说明:向量共线的充要条件强调b为非零向量,若b为零向量,则a=λb中的a只能为0,没有研究的意义.
探究
【做一做3】 若非零空间向量e1,e2不共线,则使2ke1-e2与e1+2(k+1)e2共线的k的值为 .?
解析:由题可知,2ke1-e2≠0,且e1+2(k+1)e2≠0.
若2ke1-e2与e1+2(k+1)e2共线,则存在实数λ,
使得2ke1-e2=λ[e1+2(k+1)e2]成立.
解:如图,取AC的中点记为G,连接EG,FG,
思考:我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的。那么,什么情况下三个空间向量共面呢?
在立体几何的学习中我们学习了异面直线与共面直线,那么向量之间有没有共面的情况呢?
如果直线OA平行于平面α或在平面α内,那么称向量a平行于平面α。平行于同一平面的向量,叫做共面向量。
探究:
题型四、向量共面问题
1.设a,b是两个不共线的向量,λ,μ∈R,若λa+μb=0,则( )
A.a=b=0 B.λ=μ=0
C.λ=0,b=0 D.μ=0,a=0
解析:∵a,b是两个不共线的向量,
∴a≠0,b≠0,
故只有B正确.
答案:B
重难点:1.会用图形说明空间向量加法、减法、数 乘向量及它们的运算律.
2.能运用空间向量的运算意义及运算律解 决简单的立体几何问题.
与平面向量一样:
一、空间向量的概念
(1)向量:在空间中,具_________和______的量.
(2)向量a的长度或模:表示向量a的有向线段的长度,记作|a|.
(3)零向量:长度为______的向量。(手写记作 )
单位向量:长度为_______的向量。
(4)相等向量:在空间,方向相同且模相等的向量。
(5)相反向量:长度_______方向________的向量。
(6)共线向量或平行向量:如果表示若干空间向量的有向线段所在的直线互相平行或重合。
规定:零向量与任意向量共线.
大小
方向
做一做1、正方体ABCD - A'B'C'D'中与向量相等的向量有_____
1
相等
相反
0
3
已知空间向量 ,以任意点O为起点 ,作向量 ,我们就可以把他们平移到同一平面 ,这样任意的两个空间向量的运算就可以转化为平面向量运算。由此,我们把平面向量的运算推广到空间,定义空间向量的加减法以及数乘运算:
A.1个 B.2个
C.3个 D.4个
【例1】 如图,已知长方体ABCD-A'B'C'D',化简下列向量表达式,并在图中画出化简结果的向量.
反思运用法则进行向量的线性运算时要注意关键的要素:
(1)向量加法的三角形法则:“首尾相接,指向终点”;
(2)向量减法的三角形法则:“起点重合,指向被减向量”;
(3)平行四边形法则:“起点重合”;
(4)多边形法则:“首尾相接,指向终点”.
运算律
与平面向量一样,空间向量的线性运算满足以下运算律((λ∈R,μ∈R):
(1)结合律 (a+b)+c=a+(b+c);
(2)交换律 a+b=b+a.
(3)分配律 λ(a+b)=λa+λb,(λ+μ)a=λa+μa(λ∈R,μ∈R);
说明:空间向量的加法、减法运算满足平行四边形法则或三角形法则,并且空间向量的加法满足交换律和结合律.
答案:0
反思数乘向量的运算一般是结合所给几何体,联系数乘向量的几何意义转化为一个新的向量.若同时涉及几个数乘向量,则还要注意数乘向量运算律的运用.
共线向量定理: 空间两个向量a与b(b≠0)共线的充要条件是存在实数λ,使得a=λb.
说明:向量共线的充要条件强调b为非零向量,若b为零向量,则a=λb中的a只能为0,没有研究的意义.
探究
【做一做3】 若非零空间向量e1,e2不共线,则使2ke1-e2与e1+2(k+1)e2共线的k的值为 .?
解析:由题可知,2ke1-e2≠0,且e1+2(k+1)e2≠0.
若2ke1-e2与e1+2(k+1)e2共线,则存在实数λ,
使得2ke1-e2=λ[e1+2(k+1)e2]成立.
解:如图,取AC的中点记为G,连接EG,FG,
思考:我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的。那么,什么情况下三个空间向量共面呢?
在立体几何的学习中我们学习了异面直线与共面直线,那么向量之间有没有共面的情况呢?
如果直线OA平行于平面α或在平面α内,那么称向量a平行于平面α。平行于同一平面的向量,叫做共面向量。
探究:
题型四、向量共面问题
1.设a,b是两个不共线的向量,λ,μ∈R,若λa+μb=0,则( )
A.a=b=0 B.λ=μ=0
C.λ=0,b=0 D.μ=0,a=0
解析:∵a,b是两个不共线的向量,
∴a≠0,b≠0,
故只有B正确.
答案:B
